|
--- |
|
license: other |
|
license_name: qwen |
|
base_model: Qwen/Qwen2.5-Math-72B |
|
license_link: https://huggingface.co/Qwen/Qwen2.5-Math-72B-Instruct/blob/main/LICENSE |
|
language: |
|
- en |
|
pipeline_tag: text-generation |
|
tags: |
|
- chat |
|
library_name: transformers |
|
--- |
|
|
|
|
|
# Qwen2.5-Math-72B-Instruct |
|
|
|
> [!Warning] |
|
> <div align="center"> |
|
> <b> |
|
> 🚨 Qwen2.5-Math mainly supports solving English and Chinese math problems through CoT and TIR. We do not recommend using this series of models for other tasks. |
|
> </b> |
|
> </div> |
|
|
|
## Introduction |
|
|
|
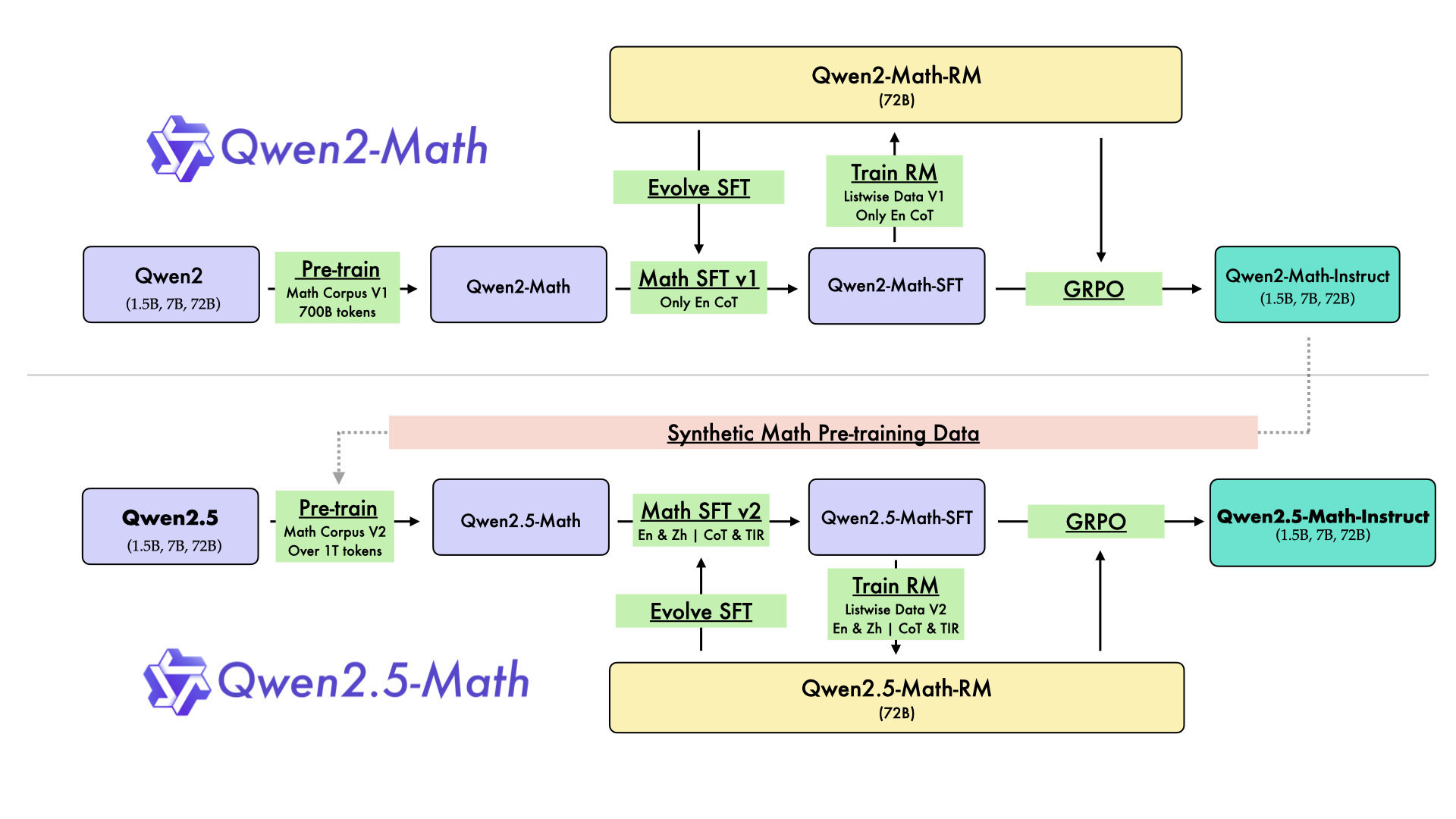
In August 2024, we released the first series of mathematical LLMs - [Qwen2-Math](https://qwenlm.github.io/blog/qwen2-math/) - of our Qwen family. A month later, we have upgraded it and open-sourced **Qwen2.5-Math** series, including base models **Qwen2.5-Math-1.5B/7B/72B**, instruction-tuned models **Qwen2.5-Math-1.5B/7B/72B-Instruct**, and mathematical reward model **Qwen2.5-Math-RM-72B**. |
|
|
|
Unlike Qwen2-Math series which only supports using Chain-of-Thught (CoT) to solve English math problems, Qwen2.5-Math series is expanded to support using both CoT and Tool-integrated Reasoning (TIR) to solve math problems in both Chinese and English. The Qwen2.5-Math series models have achieved significant performance improvements compared to the Qwen2-Math series models on the Chinese and English mathematics benchmarks with CoT. |
|
|
|
 |
|
|
|
While CoT plays a vital role in enhancing the reasoning capabilities of LLMs, it faces challenges in achieving computational accuracy and handling complex mathematical or algorithmic reasoning tasks, such as finding the roots of a quadratic equation or computing the eigenvalues of a matrix. TIR can further improve the model's proficiency in precise computation, symbolic manipulation, and algorithmic manipulation. Qwen2.5-Math-1.5B/7B/72B-Instruct achieve 79.7, 85.3, and 87.8 respectively on the MATH benchmark using TIR. |
|
|
|
## Model Details |
|
|
|
|
|
For more details, please refer to our [blog post](https://qwenlm.github.io/blog/qwen2.5-math/) and [GitHub repo](https://github.com/QwenLM/Qwen2.5-Math). |
|
|
|
|
|
## Requirements |
|
* `transformers>=4.37.0` for Qwen2.5-Math models. The latest version is recommended. |
|
|
|
> [!Warning] |
|
> <div align="center"> |
|
> <b> |
|
> 🚨 This is a must because <code>transformers</code> integrated Qwen2 codes since <code>4.37.0</code>. |
|
> </b> |
|
> </div> |
|
|
|
For requirements on GPU memory and the respective throughput, see similar results of Qwen2 [here](https://qwen.readthedocs.io/en/latest/benchmark/speed_benchmark.html). |
|
|
|
## Quick Start |
|
|
|
> [!Important] |
|
> |
|
> **Qwen2.5-Math-72B-Instruct** is an instruction model for chatting; |
|
> |
|
> **Qwen2.5-Math-72B** is a base model typically used for completion and few-shot inference, serving as a better starting point for fine-tuning. |
|
> |
|
|
|
### 🤗 Hugging Face Transformers |
|
|
|
Qwen2.5-Math can be deployed and infered in the same way as [Qwen2.5](https://github.com/QwenLM/Qwen2.5). Here we show a code snippet to show you how to use the chat model with `transformers`: |
|
|
|
```python |
|
from transformers import AutoModelForCausalLM, AutoTokenizer |
|
|
|
model_name = "Qwen/Qwen2.5-Math-72B-Instruct" |
|
device = "cuda" # the device to load the model onto |
|
|
|
model = AutoModelForCausalLM.from_pretrained( |
|
model_name, |
|
torch_dtype="auto", |
|
device_map="auto" |
|
) |
|
tokenizer = AutoTokenizer.from_pretrained(model_name) |
|
|
|
prompt = "Find the value of $x$ that satisfies the equation $4x+5 = 6x+7$." |
|
|
|
# CoT |
|
messages = [ |
|
{"role": "system", "content": "Please reason step by step, and put your final answer within \\boxed{}."}, |
|
{"role": "user", "content": prompt} |
|
] |
|
|
|
# TIR |
|
messages = [ |
|
{"role": "system", "content": "Please integrate natural language reasoning with programs to solve the problem above, and put your final answer within \\boxed{}."}, |
|
{"role": "user", "content": prompt} |
|
] |
|
|
|
text = tokenizer.apply_chat_template( |
|
messages, |
|
tokenize=False, |
|
add_generation_prompt=True |
|
) |
|
model_inputs = tokenizer([text], return_tensors="pt").to(device) |
|
|
|
generated_ids = model.generate( |
|
**model_inputs, |
|
max_new_tokens=512 |
|
) |
|
generated_ids = [ |
|
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids) |
|
] |
|
|
|
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0] |
|
``` |
|
|
|
## Citation |
|
|
|
If you find our work helpful, feel free to give us a citation. |
|
|
|
``` |
|
@article{yang2024qwen25mathtechnicalreportmathematical, |
|
title={Qwen2.5-Math Technical Report: Toward Mathematical Expert Model via Self-Improvement}, |
|
author={An Yang and Beichen Zhang and Binyuan Hui and Bofei Gao and Bowen Yu and Chengpeng Li and Dayiheng Liu and Jianhong Tu and Jingren Zhou and Junyang Lin and Keming Lu and Mingfeng Xue and Runji Lin and Tianyu Liu and Xingzhang Ren and Zhenru Zhang}, |
|
journal={arXiv preprint arXiv:2409.12122}, |
|
year={2024} |
|
} |
|
``` |