Datasets:

NMashalov

/

ruArxivmmd

like 0

## 1 Introduction The experimental evidence for neutrino mass, acquired in recent decades, provides concrete evidence for physics beyond the Standard Model (SM) (see e.g. [1]). Although the requisite new degrees of freedom cannot yet be determined it is clear that additional particles are likely to exist, in order to generate the masses. Similarly, there is by now a large amount of evidence for an additional galactic constituent, an unknown substance referred to as dark matter (see e.g. [2]). This may or may not require new degree’s of freedom, but the hypothesis that the dark matter is comprised of a stable (or long lived) new particle species provides a simple explanation for this observed feature of the Universe. Given that these two indicators for beyond-SM physics can be explained by extending the particle spectrum of the SM, it is natural to ask if the requisite new particles can be related. Could the mechanism of neutrino mass be related to the existence of a stable dark-matter candidate? A particularly simple model realizing this idea was proposed by Ma in 2006 [3]. This model extends the SM to include an additional SM-like scalar doublet and gauge-singlet fermions, all of which are odd under a discrete \(Z_{2}\) symmetry. The extended field content allows for radiative neutrino mass, generated at the one-loop level, while the lightest beyond-SM field is absolutely stable. One thus arrives at a simple synergetic model of radiative neutrino mass and dark matter. In this work we generalize Ma’s approach. We present a class of related models, all of which generate neutrino mass via a loop diagram with the same topography as Ma’s, whilst simultaneously admitting stable dark-matter candidates. The loop-diagram employed by Ma contains a mass insertion on the internal fermion line (see Figure 1), and our generalizations fall naturally into two categories; those which break lepton-number symmetry via a Majorana mass insertion, and those with a Dirac mass insertion, such that lepton-number symmetry is broken at a vertex. Although the basic mechanism is very similar in both cases, this difference modifies one’s expectations for the beyond-SM field content and the associated phenomenology. It turns out that, in both cases, this approach is very general and many realizations are possible. However, restricting attention to models in which the beyond-SM multiplets are no larger than the adjoint representation significantly reduces the possibilities. As we shall see, there are only two such (minimal) models with a Majorana mass-insertion, both of which are known [3, 4]. We find seven additional models with a mass insertion of the Dirac type, all of which achieve radiative neutrino mass and dark-matter candidates. We detail these models, finding a subset that are compatible with direct-detection experiments. There are cases with an inert singlet, an inert doublet, and an inert triplet; the models therefore provide a natural setting for inert \(N\)-tuplet theories of dark matter, such that radiative neutrino mass is also achieved. Interestingly, three of the new models admit a simple extension that can explain the origin of the (formerly imposed) discrete symmetry. By upgrading the discrete symmetry to a gauged \(U(1)\) symmetry, and extending the field content by a single SM-singlet scalar, the discrete symmetry can arise as an accidental symmetry of the low-energy Lagrangian, after \(U(1)\) symmetry breaking takes place. This provides a simple explanation for the discrete symmetry. Though we focus on models with representations no larger than the adjoint, we also briefly discuss cases where the beyond-SM fields can be quadruplet and/or quintuplet representations of \(SU(2)_{L}\). We present the candidate models in these cases, and mention some key issues, based on the lessons learned from our preceding studies. Despite the use of larger multiplets, these models can still be of interest; in addition to allowing for radiative neutrino mass, the exotics with larger electric-charges in these multiplets can enhance the \(2\gamma\) and/or \(\gamma+Z\) signal from dark-matter annihilation when they appear inside loops [5]. This can provide a simple connection between the mechanism of neutrino mass and the astrophysical gamma-ray signal [6]. Before proceeding we note that the connection between radiative neutrino mass and dark matter has been explored in a number of different models, including Ref. [7], which precedes Ma’s work; for other examples see [8]. Previous works on inert-singlet models [9], inert-doublet models [10], and inert-triplet models [11] are also well known. Additional relevant works dealing with inert-multiplet dark matter and/or radiative neutrino mass are cited in the text. Note also that Refs. [12, 13] have detailed the one-loop realizations of the \(d=5\) operator for neutrino mass. Inert scalar dark matter can also help cure the little hierarchy problem found in low-scale seesaws [14]. The present work follows on from the generalized tree-level seesaws presented in Ref. [15]. The plan of this paper is as follows. In Section 2 we discuss Ma’s model and present the generalizations that similarly achieve radiative neutrino mass and dark-matter candidates. Section 3 considers the case of fermionic dark-matter, while Section 4 discusses scalar dark-matter. One of the generalized models is presented in more detail in Section 5. In Section 6 we show that some of the models allow a simple extension, such that the discrete symmetry appears as an accidental symmetry in the low-energy theory. Models with exotics forming larger \(SU(2)\) representations are discussed in Section 7 (and explicitly displayed in the Appendix). We conclude in Section 8. [FIGURE:S1.F1][ENDFIGURE] ## 2 Radiative Neutrino Mass and Dark Matter We are interested in the class of models that generate neutrino mass radiatively by the diagram in Figure 1. Here \(\mathcal{F}\) is a beyond-SM fermion and \(S_{1,2}\) are new scalars (which can be identical in some cases). A basic feature of this diagram is that the three vertices can all involve two beyond-SM fields. Consequently one can always consider a discrete \(Z_{2}\) symmetry whose action on the beyond-SM multiplets is \[\{\mathcal{F},\;S_{1},\;S_{2}\} \rightarrow -\ \{\mathcal{F},\;S_{1},\;S_{2}\}\;,\] (1) while all SM fields transform trivially. The lightest field within the multiplets \(\mathcal{F}\) and \(S_{1,2}\) will thus be stable, and provided this field is electrically neutral and colorless, one arrives at a dark-matter candidate. These comments are generic for all models of this type; the connection between loop masses and dark matter is simple to realize in this class of models. Figure 1 produces Majorana neutrino masses, so the loop diagram must contain a source of lepton number violation. Choosing the convention for lepton-number symmetry such that the new fermion \(\mathcal{F}\) has the same value as the SM leptons, there are two ways to explicitly break lepton-number symmetry; it can be broken at either the mass insertion or at one of the vertices. The simplest models, in terms of the requisite number of beyond-SM multiplets, are those with a lepton number violating (Majorana) mass insertion. In this case one has \(\mathcal{F}_{L}\equiv\mathcal{F}_{R}^{c}\) and minimal cases occur for \(S_{1}=S_{2}\equiv S\). Thus, only two beyond-SM multiplets are required. The general loop-diagram for this subset of models is given in Figure 2. We consider this case first. ### Models with a Majorana Mass Insertion We seek models that achieve neutrino mass via Figure 2 and give rise to dark-matter candidates. Clearly the fermion must form a real representation of the SM gauge symmetry, \(\mathcal{F}_{R}\sim(1,R_{\mathcal{F}},0)\), in order to allow a bare Majorana mass. As we are considering dark-matter candidates we do not consider colored fields. Note also that \(R_{\mathcal{F}}\) must be odd-valued to ensure there is no fractionally charged particles (the lightest of which would be stable and thus cosmologically excluded). Odd-valued \(R_{\mathcal{F}}\) also ensures that \(\mathcal{F}_{R}\) contains an electrically neutral component, so no additional constraint is imposed by this demand. With this information one can obtain the viable combinations of \(\mathcal{F}_{R}\) and \(S\) that generate Figure 2. The basic Lagrangian terms are \[\mathcal{L} \supset i\bar{\mathcal{F}_{R}}\gamma^{\mu}D_{\mu}\mathcal{F}_{R}-\frac{M _{\mathcal{F}}}{2}\;\overline{\mathcal{F}_{R}^{c}}\mathcal{F}_{R}+|D^{\mu}S|^{ 2}-M_{S}^{2}|S|^{2}+\lambda\bar{L}\tilde{S}\mathcal{F}_{R}+\lambda_{\text{ \tiny SH}}(S^{\dagger}H)^{2}+\mathrm{H.c.},\] (2) where \(L\) (\(H\)) is the SM lepton (scalar) doublet and \(\tilde{S}\) denotes the charge-conjugate of \(S\). It turns out that the possible combinations for \(\mathcal{F}\) and \(S\) are not restricted by quantum numbers; one can consider increasingly large multiplets, presumably up to some unitarity limits [16], and realize a model with Figure 2 and a dark-matter candidate. However, if we restrict our attention to models with \(R_{\mathcal{F}},R_{S}\leq 3\), such that no new multiplet is larger than the adjoint representation, there are only two possibilities. The first case is Ma’s original proposal, which employs an additional (inert) scalar doublet \(S\sim(1,2,1)\), and a gauge-singlet fermion \(\mathcal{F}_{R}\sim(1,1,0)\)[3]. This model is the prototype for the class we are considering. The second model also employs the scalar doublet \(S\sim(1,2,1)\), but instead utilizes the triplet fermion \(\mathcal{F}_{R}\sim(1,3,0)\)[4], familiar from the Type-III seesaw [17]. Thus, both of the models are known in the literature, and there are no additional possibilities unless one considers larger multiplets. In each of these models the dark-matter candidate can be a neutral component of \(S\) or a Majorana fermion. There is, however, an important difference between the singlet case, \(\mathcal{F}\sim(1,1,0)\), and the other model; the singlet does not participate in weak interactions and is therefore brought into thermal contact with the SM sector via the Yukawa coupling. For fermionic dark-matter, this can produce conflict between the need to keep the Yukawa coupling large to ensure thermal dark-matter, and the need to suppress the Yukawa coupling to limit the size of flavor changing effects. This issue does not arise in the triplet fermion model, as the fermions can maintain equilibrium with the SM sector via weak interactions in these cases, even if the Yukawa couplings are suppressed. For an analysis of Ma’s model, incorporating recent LHC data on the Higgs, see e.g. Ref. [18]. Also note that loop effects can induce observable interactions between dark matter and experimental detectors in Ma’s model [19]. [FIGURE:S2.F2][ENDFIGURE] ### Models with a Dirac Mass Insertion Having exhausted the minimal models with a lepton-number violating mass insertion, we now consider models with a Dirac mass insertion; i.e. the beyond-SM fermion has nonzero hypercharge. In this case the general mass-diagram has the form shown in Figure 1. The fields \(\mathcal{F}_{R}\) and \(\mathcal{F}_{L}\) are no longer related by charge conjugation, so the mass insertion is of the Dirac type and \(\mathcal{F}\) is a vector-like fermion. In addition one requires \(S_{1}\neq S_{2}\). We again consider a \(Z_{2}\) symmetry under which the SM fields transform trivially but the new fields are odd. The Lagrangian contains the following pertinent terms: \[\mathcal{L} \supset i\bar{\mathcal{F}}\gamma^{\mu}D_{\mu}\mathcal{F}\ -\ M_{\mathcal {F}}\;\overline{\mathcal{F}}\mathcal{F}\ +\ \sum_{i=1,2}\left\{|D^{\mu}S_{i}|^ {2}\ -\ M_{i}^{2}|S_{i}|^{2}\right\}\] (3) \[+\ \lambda_{1}\;\bar{L}\mathcal{F}_{R}S_{1}\ +\ \lambda_{2}\;\bar {L}\mathcal{F}^{c}_{L}\tilde{S}_{2}\ +\ \lambda_{\text{\tiny SH}}\;S_{1}\tilde {S}_{2}H^{2}+\mathrm{H.c.},\] where, in our convention, lepton number symmetry is broken by a Yukawa coupling. With the \(Z_{2}\) symmetry present, there are no terms in the scalar potential that are linear in _just one_ of the new scalars \(S_{1,2}\). Therefore the beyond-SM scalars do not acquire an induced VEV and parameter space exists for which \(\langle S_{1,2}\rangle=0\), so the \(Z_{2}\) symmetry remains exact. In selecting viable multiplets one must ensure that no new multiplet contains a fractionally charged field, to avoid a (cosmologically excluded) stable charged field. To ensure that the lightest \(Z_{2}\)-odd field is a neutral dark-matter candidate one must demand that the new multiplets contain at least one neutral field. Note that the neutral field does not have to appear as an explicit propagating degree of freedom inside the loop diagram; it is sufficient merely that the loop-diagram exists and that the particle content includes a neutral field that can play the role of dark matter. With these conditions in mind we search for viable combinations of the beyond-SM multiplets that realize Figure 1. We find that the size of the beyond-SM multiplets is not restricted by our demands; one can consider increasingly large multiplets and realize the loop diagram. However, if attention is restricted to models in which none of the beyond-SM multiplets are larger than the adjoint representation, only seven distinct models are found. These are listed in Table 1. Of the seven models, one employs the exotic lepton triplet \(\mathcal{F}\sim(1,3,-2)\), studied in Refs. [20, 21], three contain an exotic vector-like (and SM-like) lepton doublet \(\mathcal{F}\sim(1,2,-1)\)[21, 22, 23], and two contain a charged lepton doublet \(\mathcal{F}\sim(1,2,-3)\)[21, 24]. There is also a model with a SM-like charged singlet fermion, \(\mathcal{F}\sim(1,1,-2)\), which already appeared in Ref. [25]. Neutrino masses take a standard calculable form in these models. For example, in models \((A)\) and \((B)\) only singly-charged exotics propagate in the loop, and the SM neutrino mass matrix is given by³ [FOOTNOTE:3][ENDFOOTNOTE] \[(\mathcal{M}_{\nu})_{\alpha\beta} \simeq \frac{\left[(\lambda_{2}^{*})^{a}_{\alpha}(\lambda_{1}^{*})^{a}_{ \beta}+(\lambda_{2}^{*})^{a}_{\beta}(\lambda_{1}^{*})^{a}_{\alpha}\right]}{32 \pi^{2}}\,\frac{\lambda_{\text{\tiny SH}}\langle H\rangle^{2}}{M_{>}^{2}-M_{<} ^{2}}\left[\frac{M^{2}_{>}\,M_{\mathcal{F},a}}{M_{\mathcal{F},a}^{2}-M_{>}^{2} }\,\log\frac{M_{\mathcal{F},a}^{2}}{M_{>}^{2}}\ -\ (M_{>}\to M_{<})\right]\] Here \(M_{\mathcal{F},a}\) is the mass for the charged component of the exotic fermion \(\mathcal{F}_{a}\), and summation is implied for the repeated index \(a\) (which labels the exotic-fermion generations).⁴ The masses \(M_{>,<}\) refer to the charged scalar mass-eigenstates, which are linear combinations of the charged scalars \(S_{1}^{+}\) and \(S_{2}^{+}\). The mixing results from the \(\lambda_{\text{\tiny SH}}\)-term in Eq. (3), which takes the explicit form \(\lambda_{\text{\tiny SH}}\tilde{H}^{\dagger}S_{1}S_{2}^{\dagger}H\subset \mathcal{L}\), for models \((A)\) and \((B)\). If all the exotics are at the TeV scale one requires dimensionless couplings of \(\mathcal{O}(10^{-3})\) to obtain \(m_{\nu}\sim 0.1\) eV. The scenario with all exotics at the TeV scale is most interesting from a phenomenological perspective. However, strictly speaking one only requires the lightest exotic to have a mass of \(\lesssim\mathcal{O}(\mathrm{TeV})\) in order to realize a dark-matter candidate. The other exotics can be much heavier, allowing larger dimensionless couplings. [FOOTNOTE:4][ENDFOOTNOTE] Before moving on to discuss dark matter in detail, we note that, of the models in Table 1, only models \((A)\), \((B)\) and \((D)\) are expected to produce (dominant) radiative neutrino masses in the absence of the \(Z_{2}\) symmetry, as we briefly discuss in Appendix A. [TABLE:S2.T1][ENDTABLE] ## 3 Inert Fermionic Dark Matter We now turn our attention to the dark-matter candidates in these models. It is _a priori_ possible that both fermionic and scalar dark-matter candidates are possible, as in Ma’s original proposal [3]. In this section we consider fermionic dark-matter. Note that not all the models contain neutral beyond-SM fermions; specifically, model \((A)\) has \(\mathcal{F}\sim(1,1,-2)\), and models \((F)\) and \((G)\) use \(\mathcal{F}\sim(1,2,-3)\). In these cases all beyond-SM fermions are charged and only scalar dark-matter is possible. One can already exclude the parameter space with light fermions in these models, namely \(M_{\mathcal{F}}<M_{1,2}\), due to the appearance of a stable charged-fermion. On the other hand, models \((B)\) through \((E)\) all contain neutral fermions and can, in principle, admit fermionic dark-matter. However, all of the fermion multiplets in these models have nonzero hypercharge, which can lead to strong constraints from direct-detection experiments. More precisely, if the dark-matter abundance is generated by a standard thermal WIMP one can exclude Dirac-fermion dark-matter with nonzero hypercharge, due to the strong constraints from e.g. XENON100 [26]. Thus, it is important to determine whether the neutral fermion is Dirac or Majorana. At tree-level the fermion \(\mathcal{F}\) remains a Dirac particle. However, its coupling to the SM neutrinos, which obtain Majorana masses via Figure 1, leads to a small radiative Majorana-mass. For the case of \(\mathcal{F}\sim(1,3,-2)\), the typical diagram is shown in Figure 3. Similar diagrams can occur for models \((C)\) through \((E)\), though the scalar \(S_{1}\) is real in these cases. The loop-induced Majorana mass will, in general, split the Dirac fermion \(\mathcal{F}\) into a pair of Majorana fermions. However, one can already see that the mass-splitting will be very small. The sub-loop in Figure 3 is the same loop-diagram that generates SM neutrino masses in Figure 1. Thus, in the limit that SM neutrino masses vanish, \(m_{\nu}\to 0\), the Majorana mass for \(\mathcal{F}\) will also vanish. We therefore expect \(\Delta M_{\mathcal{F}}\propto m_{\nu}\), where \(\Delta M_{\mathcal{F}}\) is the Majorana mass for \(\mathcal{F}\). This is born out by explicit calculations. For example, with \(M_{\mathcal{F}}\ll M_{S}\), where \(M_{S}\) denotes an approximate common mass for the beyond-SM scalars, one obtains \[\Delta M_{\mathcal{F}} \sim \frac{\lambda_{1}^{2}\lambda_{11\text{\tiny H}}}{16\pi^{2}}\, \frac{\langle H\rangle^{2}}{M_{S}^{2}}\times m_{\nu},\] (5) where the Lagrangian contains the term \(\lambda_{11\text{\tiny H}}^{*}(H^{\dagger}S_{1})^{2}\subset\mathcal{L}\) to generate the uppermost vertex in Figure 3. The beyond-SM neutral fermions therefore form pseudo-Dirac particles with a tiny splitting. [FIGURE:S3.F3][ENDFIGURE] Direct detection experiments give strong constraints on spin-independent elastic-scattering events that can occur when fermionic dark-matter couples to the \(Z\) boson [26]. These constraints can be avoided if the Dirac fermion has a mass-split, as the resulting pair of Majorana fermions has non-diagonal couplings to the \(Z\) boson (to leading order). Provided the mass split exceeds the average kinetic-energy of the local dark-matter particles, \(Z\)-boson exchange with SM detectors is highly suppressed, as the heavier fermion is kinematically inaccessible. However, for the models with neutral fermions in Table 1 the mass split satisfies \[\frac{\Delta M_{\mathcal{F}}}{M_{\mathcal{F}}} < \frac{m_{\nu}}{M_{\mathcal{F}}}\ \ \lesssim\ \ 10^{-12}\quad\quad \mathrm{for}\quad M_{\mathcal{F}}=\mathcal{O}(\mathrm{TeV}),\] (6) which is (much) too small to evade direct-detection bounds, given typical DM speeds of \(v_{\text{\tiny DM}}\sim 10^{-3}\). We conclude that none of the models in Table 1 are viable when the lightest beyond-SM field is a fermion, due to either a cosmologically excluded stable charged-particle or a dark-matter candidate that contradicts direct-detection constraints. The entire region of parameter space in which a fermion is the lightest beyond-SM state is thus excluded for these models. ## 4 Inert Scalar Dark Matter With the above information we can restrict our attention to the limit \(M_{\mathcal{F}}\gg M_{1,2}\) for the models in Table 1, for which the stable particle is a scalar. In this limit the models are effectively inert \(N\)-tuplet models with the additional feature of realizing radiative neutrino mass. In this section, we consider the viability of the scalar dark-matter candidates in the different models. We first consider models \((A)\) and \((B)\), whose common features allow them to be discussed together. Both these models have a single (candidate) dark-matter multiplet, which is an inert SM-like scalar doublet, \(S_{1}\sim(1,2,1)\); i.e. an inert doublet [10]. Also, in both models the second scalar is a charged doublet, \(S_{2}=(S_{2}^{++},S_{2}^{+})^{T}\), whose components must be heavier than the dark matter. Inert-doublet dark matter is well-studied in the literature, and it is known that a viable dark-matter abundance can be realized [10]. The inert-doublet leads to three new scalars, which we denote as \(H^{\prime\pm}\), \(H^{\prime 0}\) and \(A^{0}\), and either of the last two can be the dark matter. As per usual for an inert-doublet model, the neutral components of \(S_{1}\) cannot mix with the SM Higgs in models \((A)\) and \((B)\), due to the discrete symmetry. However, the charged scalar \(S_{1}^{+}\) will mix with \(S_{2}^{+}\), as mentioned already. If this mixing is large, the phenomenology of the lightest charged-scalar will differ from that of \(H^{\prime+}\) in a standard inert-doublet model. For small mixing the lightest charged scalar will correspond mostly to \(H^{\prime+}\) and the phenomenology of \(S_{1}\) will be well approximated by a standard inert-doublet. Note that one cannot take the limit \(\lambda_{\text{\tiny SH}}\to 0\) without turning off the radiative neutrino mass in Figure 1. The demand that radiative neutrino mass is realized therefore requires nonzero mixing between \(S_{1}^{+}\) and \(S_{2}^{+}\). However, given that \(S_{2}\) must be heavier than the dark-matter, one generally expects the mixing to be of order \(\langle H^{0}\rangle^{2}/M_{2}^{2}\) which is \(\lesssim 10^{-1}\) for \(M_{2}\gtrsim\) TeV. Thus, \(S_{1}\) can be well-approximated by a standard inert-doublet. The inert-doublet model contains five main regions of parameter space in which the observed relic-abundance is obtained [27]. Four of these have a light particle-spectrum that can be probed at the LHC. The discovery of an SM-like scalar with mass of roughly \(125\) GeV at the LHC allows one to update the viable parameter space and phenomenology of the inert-doublet models. Recent analysis, incorporating the LHC data, shows that the low-mass regions for the dark-matter candidate can already be in tension with constraints from XENON100 [26] and WMAP [28], while the heavier region with \(M_{\text{\tiny DM}}\gtrsim 500\) GeV is essentially unaffected [29]. Specifically, the surviving region for lighter dark-matter lies close to the Higgs-resonance/\(WW\)-production threshold [29]. The region of parameter space with \(M_{\text{\tiny DM}}=\mathcal{O}(10)\) GeV is particularly interesting for the present models as, in this case, the additional beyond-SM multiplets can be light enough to appear at the LHC. This was discussed already in Ref. [25] for model \((A)\), where it was shown that the charged scalar-doublet \(S_{2}\sim(1,2,3)\) can produce observable signals when the inert-doublet dark matter is light. Although the region of parameter space with heavier dark-matter (\(M_{\text{\tiny DM}}\gtrsim 500\) GeV) will not be accessible at the LHC, it is expected that XENON-1T will probe this parameter space, potentially giving observable direct-detection signals [30]. One deduces that viable dark matter is possible in both models \((A)\) and \((B)\), and that the combined (projected) LHC and XENON-1T data sets are expected to probe the viable parameter space in these models. We note that, in general, models with hypercharge-less dark matter are not as strongly constrained by direct-detection experiments. Such candidates do not couple directly to the \(Z\) boson so interactions with detectors do not arise at tree-level. Provided the mass-splitting between the charged and neutral components of the dark-matter multiplet exceeds the average kinetic-energy of the dark matter in the local halo, interactions with the \(W\) boson are also highly suppressed (or absent). Even if the neutral and charged components of a dark-matter multiplet are degenerate at tree-level, an \(\mathcal{O}(100)\) MeV split is induced radiatively, which is sufficient to ensure scattering via \(W\) boson exchange is suppressed/absent. These comments apply to model \((D)\), in which the sole dark-matter candidate is the neutral component of the inert real-triplet, \(S_{1}\sim(1,3,0)\). The neutral component of this multiplet does not interact with the \(Z\) boson, and the charged component can be sufficiently split (by radiative effects) to ensure the neutral state is the lightest field. This alleviates potential tension with direct-detection experiments. The possibility of inert real-triplet dark matter is well known in the literature [11, 31, 32, 33]. The neutral component of \(S_{1}\) is a viable cold dark-matter candidate that saturates the observed relic abundance of \(\Omega_{\text{\tiny CDM}}\hat{h}^{2}\simeq 0.11\)[28] for \(M_{\text{\tiny DM}}\approx 2.5\) TeV [11]. If the real-triplet is lighter it can only comprise part of the dark-matter abundance and additional candidates are needed. In model \((D)\) the dark-matter abundance must be comprised solely of \(S_{1}\), so that \(M_{\text{\tiny DM}}\approx 2.5\) TeV is a necessary requirement for this model. Unfortunately this makes it difficult to directly produce the exotic states at the LHC; both \(\mathcal{F}\sim(1,2,-1)\) and \(S_{2}\sim(1,1,2)\) must be heavier than \(2.5\) TeV to ensure the dark matter is the lightest exotic, pushing them beyond projected experimental reach. Model \((D)\) is, however, a viable model of dark matter and radiative neutrino mass for \(M_{\text{\tiny DM}}\approx 2.5\) TeV. Next we turn our attention to models \((F)\) and \((G)\), which both employ \(\mathcal{F}\sim(1,2,-3)\) and \(S_{1}\sim(1,3,2)\). In both models \(S_{2}\) is comprised purely of electrically-charged fields, so the neutral component of \(S_{1}\) is the sole dark-matter candidate. This complex neutral-field cannot mix with the SM scalar, due to the \(Z_{2}\) symmetry, so its particle and antiparticle sates remain degenerate. The dark-matter abundance is therefore comprised of both states, posing a serious difficulty for these models. Due to the nonzero hypercharge for \(S_{1}\), the neutral field can scatter off SM-detectors via tree-level \(Z\)-boson exchange. This process is strongly constrained by direct-detection data sets. Previous works show that one requires a mass of \(\sim 2.6\) TeV to obtain the correct abundance, however, the spin-independent cross-section exceeds \(10^{-37}\)cm\({}^{2}\) in the regions of parameter space compatible with the LEP experiments [32, 33]. Such a large cross section is incompatible with the constraints from, e.g., XENON100 [26]. Thus, although one can successfully generate the requisite dark-matter abundance, direct-detection constraints prove fatal for models \((F)\) and \((G)\) and both models can be excluded. It remains for us to consider models \((C)\) and \((E)\). These models admit two distinct scalar dark-matter candidates and thus allow more possibilities, as we shall see in following section. ## 5 Models with a Real Scalar and a Complex Triplet Models \((C)\) and \((E)\) both employ the SM-like fermion \(\mathcal{F}\sim(1,2,-1)\) and the complex scalar triplet \(S_{2}\sim(1,3,2)\). Furthermore, in both cases \(S_{1}\) is a real scalar. These models differ from the other cases as both scalars now possess a neutral component, giving two dark-matter candidates. We saw that models \((F)\) and \((G)\) could be excluded precisely because the dark-matter abundance was comprised of the neutral component of the complex scalar triplet. This difficulty is avoided in models \((C)\) and \((E)\), however, due to allowed mass-mixing between the neutral components of \(S_{1}\) and \(S_{2}\). In this section we discuss model \((C)\) in some detail, to elucidate the possibilities. The analysis of model \((E)\) is rather similar, due to the related field content, and we limit ourselves to some brief comments on this model at the end of the section. Model \((C)\) contains the beyond-SM scalars \(S_{1}\sim(1,1,0)\equiv S\) and \(S_{2}\sim(1,3,2)\equiv\Delta\). The full scalar-potential can be written as \[V(H,S,\Delta) = \frac{-\mu^{2}}{2}|H|^{2}+\frac{\tilde{M}_{S}^{2}}{2}S^{2}+\tilde {M}_{\Delta}^{2}\mathrm{Tr}(\Delta^{\dagger}\Delta)+\lambda_{1}|H|^{4}+\lambda _{2}\,[\mathrm{Tr}(\Delta^{\dagger}\Delta)]^{2}\] (7) \[+\lambda_{2}^{\prime}\,\mathrm{Tr}(\Delta^{\dagger}\Delta\Delta^{ \dagger}\Delta)+\frac{\lambda_{3}}{2}S^{4}+\lambda_{4}\,|H|^{2}\,\mathrm{Tr}( \Delta^{\dagger}\Delta)+\lambda_{4}^{\prime}\,H^{\dagger}\Delta^{\dagger}\Delta H\] \[+\lambda_{5}|H|^{2}S^{2}+\lambda_{6}\,S^{2}\,\mathrm{Tr}(\Delta^{ \dagger}\Delta)+\lambda_{\text{\tiny SH}}S\left\{\tilde{H}^{\dagger}\Delta^{ \dagger}H+H^{\dagger}\Delta\tilde{H}\right\},\] where the overall phase of \(\Delta\) has been used to choose \(\lambda_{\text{\tiny SH}}\) real without loss of generality.⁵ The discrete symmetry \(\{S,\,\Delta\}\rightarrow-\{S,\,\Delta\}\) ensures there is no mass-mixing between the SM scalar and the beyond-SM fields. This symmetry also forbids terms linear in a single beyond-SM scalar, like \(H\Delta^{\dagger}H\) or \(SH^{2}\), which would otherwise induce a non-zero VEV for \(\Delta\) and \(S\) after electroweak symmetry breaking. Consequently, parameter space exists in which neither \(S\) nor \(\Delta\) acquire a VEV. The scalar \(S\) and the neutral components of \(\Delta\) will mass-mix, however, due to the \(\lambda_{\text{\tiny SH}}\) term in the potential. [FOOTNOTE:5][ENDFOOTNOTE] Expanding the neutral SM-scalar around its VEV, and expanding the neutral component of \(\Delta\) as \[H^{0}=\frac{1}{\sqrt{2}}(v+h^{0}+i\chi^{0})\quad\mathrm{and} \quad\Delta^{0}=\frac{1}{\sqrt{2}}(\Delta_{R}+i\Delta_{I}),\] (8) respectively, the mass-mixing Lagrangian for the neutral scalars is \[\mathcal{L} \supset -\frac{1}{2}\mathcal{S}^{T}\mathcal{M}^{2}\mathcal{S}.\] (9) Here the basis vector is \(\mathcal{S}=(S,\Delta_{R},\Delta_{I})^{T}\), and the squared-mass matrix has the form \[\mathcal{M}^{2}=\left(\begin{array}[]{ccc}\hidden@noalign{}\hfil \tilde{M}_{S}^{2}+\lambda_{5}v^{2}&\frac{\lambda_{\text{\tiny SH}}}{2\sqrt{2}} v^{2}&0\\ \hidden@noalign{}\hfil\frac{\lambda_{\text{\tiny SH}}}{2\sqrt{2}}v^{2}&\tilde{ M}_{\Delta}^{2}+\frac{\lambda_{4}}{2}v^{2}&0\\ \hidden@noalign{}\hfil 0&0&\tilde{M}_{\Delta}^{2}+\frac{\lambda_{4}}{2}v^{2} \end{array}\right).\] (13) Thus, the CP-odd scalar \(\Delta_{I}\) is a mass eigenstate with mass \(\tilde{M}_{\Delta}^{2}+\lambda_{4}v^{2}/2\), while the CP-even scalars \(S\) and \(\Delta_{R}\) mass-mix to produce two physical scalars that are linear combinations of these fields. The dark-matter candidate will be one of the neutral-scalar mass eigenstates. To determine which one, we must find the masses for the mixed CP-even states. Let us define \(M_{S}^{2}=\tilde{M}_{S}^{2}+\lambda_{5}v^{2}\) and \(M^{2}_{\Delta}=\tilde{M}_{\Delta}^{2}+\lambda_{4}v^{2}/2\), which are the CP-even mass eigenstates in the limit \(\lambda_{\text{\tiny SH}}\to 0\). In this limit \(\Delta_{R}\) and \(\Delta_{I}\) are degenerate and form a single complex-scalar with mass \(M^{2}_{\Delta}\). For nonzero \(\lambda_{\text{\tiny SH}}\), the CP-even mass eigenvalues can be written as \[M_{\pm}=\frac{1}{2}\left\{M_{S}^{2}+M^{2}_{\Delta}\pm\left[(M_{S }^{2}-M^{2}_{\Delta})^{2}+\frac{\lambda_{\text{\tiny SH}}^{2}}{2}v^{4}\right]^ {1/2}\right\},\] (14) where the eigenstates are related to the original fields as \[\left(\begin{array}[]{c}\hidden@noalign{}\hfil S_{+}\\ \hidden@noalign{}\hfil S_{-}\end{array}\right)=\left(\begin{array}[]{cc} \hidden@noalign{}\hfil\cos\theta&\sin\theta\\ \hidden@noalign{}\hfil-\sin\theta&\cos\theta\end{array}\right)\,\left(\begin{ array}[]{c}\hidden@noalign{}\hfil S\\ \hidden@noalign{}\hfil\Delta_{R}\end{array}\right).\] (21) Here, the mixing angle is \[\tan 2\theta = \frac{\lambda_{\text{\tiny SH}}v^{2}}{\sqrt{2}(M^{2}_{S}-M^{2}_{ \Delta})}.\] (22) In the limit where the singlet-scalar is heaviest, \(M_{S}^{2}\gg M^{2}_{\Delta}\), the mass eigenvalues are approximately \[M_{+}^{2}\simeq M_{S}^{2}+\frac{\lambda_{\text{\tiny SH}}^{2}v^{ 4}}{8M_{S}^{2}}\quad\mathrm{and}\quad M_{-}^{2}\simeq M^{2}_{\Delta}-\frac{ \lambda_{\text{\tiny SH}}^{2}v^{4}}{8M_{S}^{2}}\quad\mathrm{for}\quad M_{S}^{2 }\gg M^{2}_{\Delta}.\] (23) Noting that \(M_{-}^{2}<M^{2}_{\Delta}\), reveals that \(S_{-}\) is the lightest exotic state and is thus the DM candidate. Simple expressions are obtained for the mass eigenvectors in this limit: \[\left.\begin{array}[]{c}\hidden@noalign{}\hfil S_{+}\simeq S+ \frac{\lambda_{\text{\tiny SH}}v^{2}}{2\sqrt{2}M_{S}^{2}}\Delta_{R}\\ \\ \hidden@noalign{}\hfil S_{-}\simeq\Delta_{R}-\frac{\lambda_{\text{\tiny SH}}v^ {2}}{2\sqrt{2}M_{S}^{2}}S\end{array}\right.\quad\quad\mathrm{for}\quad M_{S}^{ 2}\gg M^{2}_{\Delta},\] (27) so that the lightest scalar \(S_{-}\) is comprised mostly of \(\Delta_{R}\). Thus, for \(M_{S}^{2}\gg M^{2}_{\Delta}\) the dark matter is comprised of \(S_{-}\), which mostly consists of the CP-even part (\(\Delta_{R}\)) of the neutral field in the scalar triplet \(S_{2}\). The mass-splitting between \(S_{-}\) and the CP-odd state \(\Delta_{I}\) is \(|\Delta M^{2}|=\lambda_{\text{\tiny SH}}^{2}v^{4}/8M_{S}^{2}\). Provided this splitting exceeds the dark-matter kinetic-energy, \(\sqrt{|\Delta M^{2}|}>\mathrm{KE}_{\text{\tiny DM}}\), the state \(\Delta_{I}\) will not be kinematically accessible via tree-level processes in direct-detection experiments. This significantly weakens the bounds on dark matter arising from a complex triplet. This also gives an upper bound on the mass parameter \(M_{S}^{2}\), beyond which the splitting between the dark matter and \(\Delta_{I}\) is so small that tree-level scattering via \(Z\) exchange is expected in present-day experiments. One finds \[M_{S} < \frac{1}{2\sqrt{2}}\,\frac{|\lambda_{\text{\tiny SH}}|\,v^{2}}{ \mathrm{KE}_{\text{\tiny DM}}}\ \simeq\ \left(\frac{|\lambda_{\text{\tiny SH}} |}{10^{-2}}\right)\,\left(\frac{10^{-3}}{v_{\text{\tiny DM}}}\right)^{2}\left( \frac{2.6~{}\mathrm{TeV}}{M_{\text{\tiny DM}}}\right)\times 10^{2}~{}\mathrm{ TeV}.\] (28) Thus, the heavier state \(S_{+}\) cannot be made arbitrarily heavy if the dark matter is to avoid exclusion via, e.g., the XENON100 data. With \(M_{\text{\tiny DM}}\equiv M_{-}=\mathcal{O}(\mathrm{TeV})\), the mass-split between \(S_{-}\) and \(\Delta_{I}\) is smaller than \(M_{\Delta}\) (the mass of \(\Delta_{I}\)). Once the temperature drops below \(M_{\Delta}\), the heavier state \(\Delta_{I}\) will decay, with the decay products necessarily containing \(S_{-}\), due to the conserved discrete-symmetry. The expression \(|\Delta M^{2}|=\lambda_{\text{\tiny SH}}^{2}v^{4}/8M_{S}^{2}\) shows that the mass-splitting between \(S_{-}\) and \(\Delta_{I}\) is bounded as \(\sqrt{|\Delta M^{2}|}\lesssim|\lambda_{\text{\tiny SH}}|\times 4\) GeV, given that \(M_{\Delta}\gtrsim 3\) TeV is needed to achieve the correct relic abundance and we are working with \(M_{S}>M_{\Delta}\). In this mass range \(\Delta_{I}\) can decay as \(\Delta_{I}\to S_{-}+Z^{*}\to S_{-}+\bar{f}f\), where \(f\) is a SM fermion with mass \(m_{f}<|\lambda_{\text{\tiny SH}}|\times 2\) GeV. Therefore, even if charged SM fermions are not kinematically available, final-states containing neutrinos will be accessible unless \(\lambda_{\text{\tiny SH}}\) is exceptionally small. After \(\Delta_{I}\) has decayed away, the primordial plasma is comprised of \(S_{-}\) and the SM fields. \(S_{-}\) can maintain equilibrium with the SM sector via gauge interactions and via the \(\lambda_{4}\) and \(\lambda_{4}^{\prime}\) (hereafter \(\lambda_{4}\)) quartic terms in Eq. (7).⁶ When the quartic interactions are dominant, the model is similar to an inert real-triplet model; the dark-matter abundance will be obtained for \(M_{\text{\tiny DM}}\simeq 2.5\) TeV, in line with the analysis of Ref. [11]. As one makes \(\lambda_{4}\) smaller, the tree-level mass splitting between the charged and neutral components of \(\Delta\) diminishes and coannihilation channels like \(\Delta^{-}\Delta^{++}\to W^{+}\gamma\) become available. At this point, making \(\lambda_{4}\) smaller does not modify the requisite dark-matter mass as gauge interactions dominate. The analysis of Ref. [33] for an inert complex-triplet finds that \(M_{\text{\tiny DM}}\gtrsim 2.8\) TeV is required for the entire region of parameter space.⁷ We thus expect that \(M_{\text{\tiny DM}}\gtrsim 2.5\) TeV will be required even when the gauge interactions dominate the quartic interactions during freeze-out for the present scenario. With this value fixed, model \((C)\) becomes a viable model of neutrino mass and dark matter. It will be difficult, however, to produce the exotics in this model, given that the lightest exotic mass is \(\gtrsim 2.5\) TeV.⁸ [FOOTNOTE:6][ENDFOOTNOTE] [FOOTNOTE:7][ENDFOOTNOTE] [FOOTNOTE:8][ENDFOOTNOTE] We now briefly discuss the alternative limit with \(M_{S}^{2}\ll M^{2}_{\Delta}\). In this case the CP-even mass eigenvalues are \[M_{+}^{2}\simeq M_{\Delta}^{2}+\frac{\lambda_{\text{\tiny SH}}^{ 2}v^{4}}{8M_{\Delta}^{2}}\quad\mathrm{and}\quad M_{-}^{2}\simeq M^{2}_{S}- \frac{\lambda_{\text{\tiny SH}}^{2}v^{4}}{8M_{\Delta}^{2}}\quad\mathrm{for} \quad M_{\Delta}^{2}\gg M^{2}_{S}.\] (29) We see that the dark-matter candidate remains as the lightest CP-even eigenstate \(S_{-}\), with mass \(M_{-}\). The mass eigenstates are now \[\left.\begin{array}[]{c}\hidden@noalign{}\hfil S_{+}\simeq\Delta_ {R}+\frac{\lambda_{\text{\tiny SH}}v^{2}}{2\sqrt{2}M_{\Delta}^{2}}S\\ \\ \hidden@noalign{}\hfil S_{-}\simeq S-\frac{\lambda_{\text{\tiny SH}}v^{2}}{2 \sqrt{2}M_{\Delta}^{2}}\Delta_{R}\end{array}\right.\quad\quad\mathrm{for}\quad M _{\Delta}^{2}\gg M^{2}_{S},\] (33) so the dark matter is comprised mostly of the singlet-scalar \(S\). Singlet-scalar dark matter is well known [9] and detailed analysis show that \(M_{\text{\tiny DM}}\gtrsim 80\) GeV is compatible with direct-detection constraints and WMAP data for a Higgs mass of \(m_{h}\simeq 125\) GeV [37]. The viable region of parameter space can be probed by XENON1T, excepting a small resonant window with \(M_{\text{\tiny DM}}\simeq 62\) GeV, where the dark-matter-Higgs coupling can be very small. Lighter dark-matter with \(M_{\text{\tiny DM}}\lesssim 60\) GeV is ruled out by LHC bounds on invisible Higgs decays [37]. We see that model \((C)\) has viable parameter space in which it behaves like an inert-triplet model or an inert singlet model. This analysis is sufficient to demonstrate that model \((E)\) also has viable regions of parameter space. In model \((E)\) one has \(S_{1}\sim(1,3,0)\), while the second scalar remains as \(S_{2}\sim(1,3,2)\). The scalar potential for this model contains a term similar to the \(\lambda_{\text{\tiny SH}}\) term in Eq. (7), which mixes the neutral component of \(S_{1}\) with the CP-even neutral component of \(S_{2}\). If \(S_{2}\) is heaviest the model behaves like an inert real-triplet model, while if \(S_{1}\) is heaviest the lightest scalar is mostly comprised of \(\Delta_{R}\) (the neutral CP-even part of \(S_{2}\)). Direct-detection constraints can be evaded due to the mass mixing, and the model is again an effective model of inert-triplet dark matter. In both cases we expect that a viable dark-matter abundance and viable neutrino masses can be obtained, though the dark matter will be heavy, with \(M_{\text{\tiny DM}}\gtrsim 2.5\) TeV (neglecting resonant regions). In terms of the observational prospects for the beyond-SM multiplets at the LHC, the limit \(M_{\Delta}^{2}\gg M^{2}_{S}\) in model \((C)\) appears to be the most optimistic scenario for the models in Table 1 (excepting the resonant regions, which also allow lighter fields). In this limit the dark matter can be relatively light, \(M_{\text{\tiny DM}}\simeq 100\) GeV, and thus the exotic states \(\Delta\) and \(\mathcal{F}\) can both be of order a few hundred GeV. In principle it could be possible to observe all three beyond-SM multiplets in this limit. For the other viable models in Table 1 the dark matter has to be relatively heavy: \(M_{\text{\tiny DM}}\gtrsim 500\) GeV for the inert doublet models, and \(M_{\text{\tiny DM}}\gtrsim 2.5\) TeV for the inert triplet cases. This pushes the additional beyond-SM fields beyond the reach of the LHC. Note that any mass degeneracy between charged and neutral members of an inert multiplet at tree-level is lifted by radiative effects, making the charged components heavier than the neutral components. The heavier members of a given multiplet can decay to lighter members of the same multiplet via the weak interactions, e.g. \(\mathcal{F}^{+}\to W^{+}+\mathcal{F}^{0}\), where the \(W\) can be virtual. A heavier multiplet can also decay to a lighter multiplet via the Yukawa coupling; e.g. \(\mathcal{F}^{-}\to S^{0}+\ell^{-}\) if \(M_{\mathcal{F}}\gg M_{S}\). Because of the discrete symmetry the new fields can only be pair produced in colliders, and conservation of the \(Z_{2}\) charge means final states resulting from exotic decay chains necessarily include stable electrically-neutral fields that will escape the detector. ## 6 On the Origin of the Discrete Symmetry Following Ma’s original proposal, we employed a discrete \(Z_{2}\) symmetry to ensure stability of the lightest beyond-SM field appearing in the neutrino-mass diagram. One can argue that the use of a discrete symmetry is not completely satisfying, either because it seems ad hoc, or because of the view that quantum gravity effects are not expected to conserve global symmetries. This motivates one to consider whether a simple explanation for the discrete symmetry can be found. The simplest possibility is to replace the discrete symmetry with a gauged \(U^{\prime}(1)\) symmetry, which would not be broken by quantum gravity effects. With enough additional ingredients one can presumably achieve this goal for all the models we have discussed. However, we would like to know which models allow for a minimal extension, such that \(Z_{2}\to U^{\prime}(1)\), and a single SM-singlet scalar \(\eta\) is added to the particle spectrum to break the \(U^{\prime}(1)\) symmetry. Writing the full gauge group as \(\mathcal{G}_{\text{\tiny SM}}\times U(1)^{\prime}\), where \(\mathcal{G}_{\text{\tiny SM}}\) is the SM gauge group, we have the following transformation properties for the beyond-SM fields⁹ [FOOTNOTE:9][ENDFOOTNOTE] \[\eta\sim(1_{\text{\tiny SM}},Q_{\eta})\,,\quad S_{1,2}\sim(Q^{ \text{\tiny SM},}_{1,2},Q)\,,\quad\mathcal{F}\sim(Q^{\text{\tiny SM}}_{ \mathcal{F}},-Q),\] (34) where the “SM” superscript denotes the charges under \(\mathcal{G}_{\text{\tiny SM}}\), given in Table 1. Inspection of Eq. (3) shows that all Lagrangian terms needed to generate neutrino mass are allowed by the \(U^{\prime}(1)\) symmetry. However, in the case of models \((A)\) and \((B)\), which are inert-doublet models, the enhanced symmetry prevents the additional term \((S_{1}^{\dagger}H)^{2}\). This term is not needed for neutrino mass but is required to split the neutral components of \(S_{1}\sim(1,2,1)\) in order to avoid direct-detection constraints [10]. Thus, models \((A)\) and \((B)\) are not compatible with this minimal symmetry extension. On the other hand, we find that models \((C)\), \((D)\) and \((E)\), which have one scalar forming a real representation of the SM gauge symmetry, remain as viable models of dark matter provided \(Q_{\eta}=-2Q\). This relationship is needed to lift a mass-degeneracy of neutral beyond-SM fields. For example, consider model \((C)\), which now has the following terms in the scalar potential \[V(H,S,\Delta,\eta) \supset \lambda_{\text{\tiny SH}}\left\{S\tilde{H}^{\dagger}\Delta^{ \dagger}H+S^{*}H^{\dagger}\Delta\tilde{H}\right\}\ +\ \frac{\mu_{\eta}}{2} \left\{S^{2}\eta+S^{*2}\eta^{\dagger}\right\},\] (35) in addition to the terms in Eq. (7). All other terms containing \(\eta\) depend only on the modulus \(|\eta|^{2}\). We have used the relative phase of \(S\) and \(\Delta\) to choose \(\lambda_{\text{\tiny SH}}\) real and the phase of \(S\) to choose \(\mu_{\eta}\) real. Note that the symmetry breaking \(U^{\prime}(1)\to Z_{2}\) is achieved by nonzero \(\langle\eta\rangle\), motivating the discrete symmetry as an accidental subgroup of the gauged \(U^{\prime}(1)\) symmetry. In the basis \(\mathcal{S}=(S_{R},\Delta_{R},S_{I},\Delta_{I})^{T}\), the squared-mass matrix has the form¹⁰ [FOOTNOTE:10][ENDFOOTNOTE] \[\mathcal{M}^{2}=\left(\begin{array}[]{cccc}\hidden@noalign{}\hfil \tilde{M}_{S}^{2}+\lambda_{5}v^{2}+2\mu_{\eta}\langle\eta\rangle&\frac{\lambda _{\text{\tiny SH}}}{4}v^{2}&0&0\\ \hidden@noalign{}\hfil\frac{\lambda_{\text{\tiny SH}}}{4}v^{2}&\tilde{M}_{ \Delta}^{2}+\frac{\lambda_{4}}{2}v^{2}&0&0\\ \hidden@noalign{}\hfil 0&0&\tilde{M}_{S}^{2}+\lambda_{5}v^{2}-2\mu_{\eta} \langle\eta\rangle&\frac{\lambda_{\text{\tiny SH}}}{4}v^{2}\\ \hidden@noalign{}\hfil 0&0&\frac{\lambda_{\text{\tiny SH}}}{4}v^{2}&\tilde{M}_ {\Delta}^{2}+\frac{\lambda_{4}}{2}v^{2}\end{array}\right).\] (40) Observe that the entries for the CP-even and CP-odd states are identical in the limit \(\mu_{\eta}\to 0\). This would produce degenerate states so that, in the case where the dark matter is comprised mostly of \(\Delta\), the dark matter would be ruled out by XENON100 (it would be an inert complex-triplet). For non-zero \(\mu_{\eta}\), however, the CP-even and CP-odd states are non-degenerate and viable dark-matter is achieved. When the dark matter is mostly (or completely, for model \((D)\)) comprised of a real representation of \(\mathcal{G}_{\text{\tiny SM}}\), the splitting achieved by nonzero \(\mu_{\eta}\) also ensures direct detection signals resulting from mixing between \(Z^{\prime}\) and \(Z\) are suppressed.¹¹ [FOOTNOTE:11][ENDFOOTNOTE] There will be an additional scattering process for the dark matter due to the mixing between \(\eta\) and the SM scalar, which gives a standard Higgs portal interaction. Given that the coupling for this interaction is not needed to achieve the observed dark-matter abundance, one can always choose this coupling to be small enough to comply with constraints. Thus, with this simple gauge extension, we can explain the origin of the discrete symmetry for models \((C)\), \((D)\) and \((E)\), while retaining the desirable features of radiative neutrino mass and a viable dark-matter abundance. Note that Ma’s original proposal [3], and the variant using a real triplet fermion [4], are not compatible with this minimal symmetry upgrade; in the case of scalar dark-matter, the \((S^{\dagger}H)^{2}\) term is precluded, meaning direct-detection experiments rule the model out, similar to the minimal gauge extension of models \((A)\) and \((B)\). Furthermore, one encounters gauge-anomalies given that \(\mathcal{F}_{R}\) is a chiral field in Refs. [3, 4] — additional model building is therefore needed to explain the origin of the \(Z_{2}\) symmetry in these cases. We do not pursue this matter here. ## 7 Beyond the Adjoint Representation In the preceding sections we studied generalizations of Ma’s 2006 model with radiative neutrino mass and stable dark-matter candidates. In doing so we restricted our attention to beyond-SM multiplets no larger than the adjoint representation. As mentioned already, one can generate neutrino mass via Figure 1 and obtain dark-matter candidates in models with larger multiplets. We briefly discuss this matter in the present section. First consider the case with a Majorana mass insertion, as in Figure 2. Allowing for \(SU(2)\) representations as large as the quintuplet-rep. we find two additional models. Both of these employ the quadruplet scalar \(S\sim(1,4,1)\), with the real fermion being either a triplet \(\mathcal{F}\sim(1,3,0)\), or a quintuplet \(\mathcal{F}\sim(1,5,0)\). The latter model was detailed in Ref. [38].¹² In both models we expect either scalar or fermionic dark-matter is possible, as in Ma’s original proposal; the neutral fermion does not couple to the \(Z\) boson and can therefore remain consistent with direct-detection constraints. [FOOTNOTE:12][ENDFOOTNOTE] Generalizing the models with a fermion mass insertion of the Dirac type (i.e. generalizing the models in Table 1), we find more variants are possible. For completeness we list these in the Appendix, but here offer the following comments. As with the models in Table 1, we find that fermionic dark-matter can be ruled out for all models with larger gauge representations. The fermions remain as pseudo-Dirac particles with tiny splittings, set by the SM neutrino masses. Such small splittings permit unsuppressed tree-level scattering with SM detectors via \(Z\)-boson exchange, which is ruled out by XENON100. We thus rule out the parameter space in which the fermion is the lightest beyond-SM state, for the same reasons as discussed in Section 3. For the case of scalar dark-matter, one has to consider the individual models, as was needed for the models in Table 1. Some models can be immediately ruled out for the same reasons that models \((F)\) and \((G)\) could be excluded; for example, model \((L)\) in Table 2 can be excluded as it gives an inert complex-triplet model. Similarly model \((R)\) in Table 3 is ruled out, as \(S_{2}\) contains only charged components and \(S_{1}\) has nonzero hypercharge. The other models appear to be compatible with direct-detection constraints, provided the neutral components of the scalars mix when the lightest scalar has nonzero hypercharge, much as models \((C)\) and \((E)\) were viable. For example, model \((M)\) contains \(S_{1}\sim(1,4,1)\) as the only beyond-SM scalar with a neutral component. However, the Lagrangian allows a term \(\lambda(S_{1}^{\dagger}H)^{2}\subset\mathcal{L}\) that can split the components of the neutral scalar, allowing one to avoid direct-detection constraints (this is analogous to the splitting obtained in an inert-doublet model). Finally, we note that the use of larger multiplets may have an additional phenomenological benefit. Ref. [5] shows that large multiplets that mediate interactions between dark matter and the SM can enhance loop-induced annihilation of dark matter into \(2\gamma\) and \(\gamma+Z\) final states, without requiring non-perturbatively large couplings. This occurs because the larger multiplets admit fields with larger electric-charges, naturally enhancing loop-processes with final-state photons. It does not appear to be possible to realize the astrophysical gamma-ray signal [6] in the models presented in the Appendix, but simple extensions do seem compatible with this idea. For example, model \((N)\) in Table 3 employs \(\mathcal{F}\sim(1,4,-1)\), \(S_{1}\sim(1,5,0)\) and \(S_{2}\sim(1,5,2)\). When \(S_{1}\) is the lightest beyond-SM state the dark matter is comprised (mostly) of the neutral component of \(S_{1}\). There is a one-loop contribution to processes like \(DM+DM\to 2\gamma,\gamma+Z\), containing virtual \(S_{2}\) states in the loop, that is enhanced by the presence of the multiply charged component in \(S_{2}\). Note that the dark-matter mass is required to be either \(M_{\text{\tiny DM}}\sim 130\) GeV or \(M_{\text{\tiny DM}}\sim 144\) GeV, in order to generate the gamma-ray excess via dark matter annihilations into either \(2\gamma\) or \(\gamma+Z\) final states, respectively. However, dark-matter comprised of \(S_{1}\sim(1,5,0)\) is expected to have a mass \(M_{\text{\tiny DM}}\gtrsim 5\) TeV in order to achieve the correct relic abundance [11], which is too large to explain the astrophysical signal. If one adds a singlet scalar \(S\), that is also odd under the \(Z_{2}\) symmetry, to the model, then the region of parameter space where \(S\) is the dark matter is compatible with \(M_{\text{\tiny DM}}\sim 130\) GeV or \(M_{\text{\tiny DM}}\sim 144\) GeV. The components of \(S_{1}\) and/or \(S_{2}\) can then be \(\mathcal{O}(100)\) GeV and the loop-processes advocated in Ref. [5] are present in the model, thereby enhancing the astrophysical gamma-ray signal.¹³ In this example there is a simple connection between the astrophysical signal and the mechanism of neutrino mass, with the large multiplets that enable the latter also enhancing the former. It could be interesting to take these ideas further to see if the dark matter can be realized as one of the fields in the neutrino loop-diagram, rather than an extra degree of freedom, or to study the phenomenology of the model just described. [FOOTNOTE:13][ENDFOOTNOTE] ## 8 Conclusion We studied a class of models with radiative neutrino mass and stable dark-matter candidates. Neutrino mass was generated by a one-loop diagram with the same topography as that proposed by Ma [3]. We generalized Ma’s approach, detailing all variants with beyond-SM fields no larger than the adjoint representation. In the case where the neutrino mass diagram contained a Majorana mass insertion, only two models were found, both of which were known. When the mass-insertion was of the Dirac type, such that lepton-number symmetry was broken by a vertex, we found a number of additional models. Fermionic dark-matter was excluded in all of these models, while two of the models were completely excluded due to direct-detection constraints. The remaining models allowed radiative neutrino mass and achieved a viable (scalar) dark-matter abundance. There were cases with an inert singlet, an inert doublet, and an inert triplet, providing a natural setting for inert \(N\)-tuplet models of dark-matter, with the additional feature of achieving radiative neutrino mass. Interestingly, some of the models allowed a simple extension, such that the (formerly imposed) discrete symmetry emerged as an accidental low-energy symmetry. We briefly discussed models with larger beyond-SM multiplets, showing that viable scenarios exist. With simple extensions, the large multiplets enabling neutrino mass can also enhance present-day astrophysical gamma-ray signals, allowing a simple connection between the mechanism of neutrino mass and the astrophysical gamma-ray signal. ## Acknowledgments The authors thank Y. Kajiyama, K. Nagao, H. Okada, T. Schwetz, A. Strumia, and K. Yagyu. SSCL is supported in part by the NSC under Grant No. NSC-101-2811-M-006-015 and in part by the NCTS of Taiwan. KM is supported by the Australian Research Council. ## Appendix A Mass Without the \(\mathbf{Z_{2}}\) Symmetry Of the models presented in Table 1, only models \((A)\), \((B)\) and \((D)\) are expected to produce (dominant) radiative neutrino masses in the absence of the \(Z_{2}\) symmetry. The other models contain the triplet scalar \(S_{1,2}\sim(1,3,2)\), which Yukawa-couples to the SM leptons, and acquires a VEV due to the term \(\mu HS_{1,2}H\subset V(H,S_{1},S_{2})\), in the absence of the discrete symmetry. Thus, tree-level neutrino masses of the standard Type-II seesaw [40] form are expected to dominate the loop effect when the \(Z_{2}\) symmetry is discarded.¹⁴ For models \((A)\), \((B)\) and \((D)\), on the other hand, tree-level neutrino masses do not arise if the \(Z_{2}\) symmetry is removed, while the loop-diagram in Figure 1 persists. Note that, if the \(Z_{2}\) symmetry is turned off, the fermion \(\mathcal{F}\) is not needed in order to generate nonzero radiative neutrino masses in model \((D)\)[41]. However, the spectrum obtained without \(\mathcal{F}\) is of the simplified-Zee form [41], which is incompatible with the observed mixing pattern [42]. Thus, the fermion \(\mathcal{F}\sim(1,2,-1)\) is required to obtain a _viable_ mixing pattern in the absence of the \(Z_{2}\) symmetry. [FOOTNOTE:14][ENDFOOTNOTE] Model \((B)\) has a similar particle content to the model presented in Ref. [43], modulo the replacement \(S_{2}\sim(1,2,3)\to S_{2}\sim(1,4,3)\). This difference precludes the tree-level mass found in Ref. [43] so model \((B)\) is purely a model of radiative masses, which could be studied without the discrete symmetry and dark matter.¹⁵ [FOOTNOTE:15][ENDFOOTNOTE] ## Appendix B Models with Larger Multiplets In the text we found seven models that employ beyond-SM multiplets in either the fundamental or adjoint representation of \(SU(2)_{L}\), and had an internal Dirac mass-insertion. In addition to these minimal models, one can realize radiative neutrino mass and dark-matter candidates with larger multiplets. We present the additional minimal models that arise if one permits multiplets forming the quadruplet (isospin-\(3/2\)) representation of \(SU(2)_{L}\) in Table 2. The labeling scheme follows on from Table 1 in the text. If one allows for quintuplet multiplets there are additional models, shown in Table 3 (also see Ref. [44] for a detailed example). The first case listed as model \((M)\) was presented in Ref. [15]. [TABLE:A2.T2][ENDTABLE] [TABLE:A2.T3][ENDTABLE] ## References * [1] M. C. Gonzalez-Garcia, M. Maltoni, J. Salvado and T. Schwetz, JHEP **1212**, 123 (2012) [arXiv:1209.3023 [hep-ph]]. * [2] A. H. G. Peter, arXiv:1201.3942 [astro-ph.CO]. * [3] E. Ma, Phys. Rev. D **73**, 077301 (2006) [hep-ph/0601225]. * [4] E. Ma and D. Suematsu, Mod. Phys. Lett. A **24**, 583 (2009) [arXiv:0809.0942 [hep-ph]]. * [5] J. Kopp, E. T. Neil, R. Primulando and J. Zupan, Phys. Dark. Univ. **2** (2013) 22 [arXiv:1301.1683 [hep-ph]]. * [6] C. Weniger, JCAP **1208**, 007 (2012) [arXiv:1204.2797 [hep-ph]]. * [7] L. M. Krauss, S. Nasri and M. Trodden, Phys. Rev. D **67**, 085002 (2003) [hep-ph/0210389]. * [8] C. Boehm, Y. Farzan, T. Hambye, S. Palomares-Ruiz and S. Pascoli, Phys. Rev. D **77**, 043516 (2008) [hep-ph/0612228]; M. Lindner, D. Schmidt and T. Schwetz, Phys. Lett. B **705**, 324 (2011) [arXiv:1105.4626 [hep-ph]]; F. -X. Josse-Michaux and E. Molinaro, Phys. Rev. D **84**, 125021 (2011) [arXiv:1108.0482 [hep-ph]]; S. Kanemura, T. Nabeshima and H. Sugiyama, Phys. Rev. D **85**, 033004 (2012) [arXiv:1111.0599 [hep-ph]]; M. Gustafsson, J. M. No and M. A. Rivera, arXiv:1212.4806 [hep-ph]; M. Aoki, J. Kubo and H. Takano, arXiv:1302.3936 [hep-ph]; Y. Kajiyama, H. Okada and T. Toma, arXiv:1303.7356 [hep-ph]. * [9] V. Silveira and A. Zee, Phys. Lett. B **161**, 136 (1985); J. McDonald, Phys. Rev. D **50** (1994) 3637 [hep-ph/0702143 [HEP-PH]]; C. P. Burgess, M. Pospelov and T. ter Veldhuis, Nucl. Phys. B **619** (2001) 709 [hep-ph/0011335]. * [10] R. Barbieri, L. J. Hall and V. S. Rychkov, Phys. Rev. D **74** (2006) 015007 [hep-ph/0603188]; L. Lopez Honorez, E. Nezri, J. F. Oliver and M. H. G. Tytgat, JCAP **0702** (2007) 028 [hep-ph/0612275]. Q. -H. Cao, E. Ma and G. Rajasekaran, Phys. Rev. D **76** (2007) 095011 [arXiv:0708.2939 [hep-ph]]; S. Andreas, M. H. G. Tytgat and Q. Swillens, JCAP **0904** (2009) 004 [arXiv:0901.1750 [hep-ph]]; L. Lopez Honorez and C. E. Yaguna, JCAP **1101** (2011) 002 [arXiv:1011.1411 [hep-ph]]; M. Gustafsson, S. Rydbeck, L. Lopez-Honorez and E. Lundstrom, Phys. Rev. D **86** (2012) 075019 [arXiv:1206.6316 [hep-ph]]; S. Kashiwase and D. Suematsu, Phys. Rev. D **86** (2012) 053001 [arXiv:1207.2594 [hep-ph]]. * [11] M. Cirelli, N. Fornengo and A. Strumia, Nucl. Phys. B **753**, 178 (2006) [hep-ph/0512090]; M. Cirelli, A. Strumia and M. Tamburini, Nucl. Phys. B **787**, 152 (2007) [arXiv:0706.4071 [hep-ph]]. * [12] E. Ma, Phys. Rev. Lett. **81** (1998) 1171 [hep-ph/9805219]. * [13] F. Bonnet, M. Hirsch, T. Ota and W. Winter, JHEP **1207**, 153 (2012) [arXiv:1204.5862 [hep-ph]]. * [14] M. Fabbrichesi and S. Petcov, arXiv:1304.4001 [hep-ph]. * [15] K. L. McDonald, JHEP **1307**, 020 (2013) [arXiv:1303.4573 [hep-ph]]. * [16] K. Hally, H. E. Logan and T. Pilkington, Phys. Rev. D **85**, 095017 (2012) [arXiv:1202.5073 [hep-ph]]. * [17] R. Foot, H. Lew, X. G. He and G. C. Joshi, Z. Phys. C **44**, 441 (1989). * [18] S. -Y. Ho and J. Tandean, arXiv:1303.5700 [hep-ph]. * [19] D. Schmidt, T. Schwetz and T. Toma, Phys. Rev. D **85**, 073009 (2012) [arXiv:1201.0906 [hep-ph]]. * [20] C. -K. Chua and S. S. C. Law, Phys. Rev. D **83**, 055010 (2011) [arXiv:1011.4730 [hep-ph]]; A. Delgado, C. Garcia Cely, T. Han and Z. Wang, Phys. Rev. D **84**, 073007 (2011) [arXiv:1105.5417 [hep-ph]]; S. S. C. Law and K. L. McDonald, Phys. Lett. B **713**, 490 (2012) [arXiv:1204.2529 [hep-ph]]; I. Baldes, N. F. Bell, K. Petraki and R. R. Volkas, arXiv:1304.6162 [hep-ph]; G. Bambhaniya, J. Chakrabortty, S. Goswami and P. Konar, arXiv:1305.2795 [hep-ph]. * [21] E. Del Nobile, R. Franceschini, D. Pappadopulo and A. Strumia, Nucl. Phys. B **826**, 217 (2010) [arXiv:0908.1567 [hep-ph]]. * [22] A. Joglekar, P. Schwaller and C. E. M. Wagner, JHEP **1212** (2012) 064 [arXiv:1207.4235 [hep-ph]]. * [23] C. Arina, R. N. Mohapatra and N. Sahu, Phys. Lett. B **720** (2013) 130 [arXiv:1211.0435 [hep-ph]]. * [24] S. S. C. Law, JHEP **1202** (2012) 127 [arXiv:1106.0375 [hep-ph]]. * [25] M. Aoki, S. Kanemura and K. Yagyu, Phys. Lett. B **702**, 355 (2011) [Erratum-ibid. B **706**, 495 (2012)] [arXiv:1105.2075 [hep-ph]]. * [26] E. Aprile _et al._ [XENON100 Collaboration], Phys. Rev. Lett. **107** (2011) 131302 [arXiv:1104.2549 [astro-ph.CO]]; Phys. Rev. Lett. **109**, 181301 (2012) [arXiv:1207.5988 [astro-ph.CO]]. * [27] E. M. Dolle and S. Su, Phys. Rev. D **80** (2009) 055012 [arXiv:0906.1609 [hep-ph]]. * [28] E. Komatsu _et al._ [WMAP Collaboration], Astrophys. J. Suppl. **192** (2011) 18 [arXiv:1001.4538 [astro-ph.CO]]. * [29] A. Goudelis, B. Herrmann and O. Stål, arXiv:1303.3010 [hep-ph]. * [30] M. Klasen, C. E. Yaguna and J. D. Ruiz-Alvarez, arXiv:1302.1657 [hep-ph]; M. Klasen, C. E. Yaguna, J. D. Ruiz-Alvarez, D. Restrepo and O. Zapata, arXiv:1302.5298 [hep-ph]. * [31] P. Fileviez Perez, H. H. Patel, M. J. Ramsey-Musolf and K. Wang, Phys. Rev. D **79**, 055024 (2009) [arXiv:0811.3957 [hep-ph]]; * [32] T. Hambye, F. -S. Ling, L. Lopez Honorez and J. Rocher, JHEP **0907** (2009) 090 [Erratum-ibid. **1005** (2010) 066] [arXiv:0903.4010 [hep-ph]]. * [33] T. Araki, C. Q. Geng and K. I. Nagao, Phys. Rev. D **83** (2011) 075014 [arXiv:1102.4906 [hep-ph]]; T. Araki, C. Q. Geng and K. I. Nagao, Int. J. Mod. Phys. D **20** (2011) 1433 [arXiv:1108.2753 [hep-ph]]. * [34] R. Foot, A. Kobakhidze, K. L. McDonald and R. R. Volkas, Phys. Rev. D **76** (2007) 075014 [arXiv:0706.1829 [hep-ph]]; R. Foot, A. Kobakhidze, K. L. McDonald and R. R. Volkas, Phys. Rev. D **77**, 035006 (2008) [arXiv:0709.2750 [hep-ph]]. * [35] Y. Kajiyama, H. Okada and K. Yagyu, arXiv:1303.3463 [hep-ph]. * [36] S. Kanemura and H. Sugiyama, Phys. Rev. D **86** (2012) 073006 [arXiv:1202.5231 [hep-ph]]. * [37] A. Djouadi, O. Lebedev, Y. Mambrini and J. Quevillon, Phys. Lett. B **709**, 65 (2012) [arXiv:1112.3299 [hep-ph]]. * [38] K. Kumericki, I. Picek and B. Radovcic, Phys. Rev. D **86**, 013006 (2012) [arXiv:1204.6599 [hep-ph]]; I. Picek and B. Radovcic, Phys. Lett. B **719**, 404 (2013) [arXiv:1210.6449 [hep-ph]]. The same model is mentioned in Y. Liao, JHEP **1106**, 098 (2011) [arXiv:1011.3633 [hep-ph]]. * [39] M. Cirelli and A. Strumia, New J. Phys. **11** (2009) 105005 [arXiv:0903.3381 [hep-ph]]. * [40] W. Konetschny and W. Kummer, Phys. Lett. B **70**, 433 (1977); T. P. Cheng and L. F. Li, Phys. Rev. D **22**, 2860 (1980); M. Magg and C. Wetterich, Phys. Lett. B **94**, 61 (1980); J. Schechter and J. W. F. Valle, Phys. Rev. D **22**, 2227 (1980); G. Lazarides, Q. Shafi and C. Wetterich, Nucl. Phys. B **181**, 287 (1981); C. Wetterich, Nucl. Phys. B **187**, 343 (1981); R. N. Mohapatra and G. Senjanovic, Phys. Rev. D **23**, 165 (1981). * [41] S. S. C. Law and K. L. McDonald, arXiv:1303.6384 [hep-ph]. * [42] X. -G. He, Eur. Phys. J. C **34**, 371 (2004) [hep-ph/0307172]. * [43] K. S. Babu, S. Nandi and Z. Tavartkiladze, Phys. Rev. D **80**, 071702 (2009) [arXiv:0905.2710 [hep-ph]]. * [44] I. Picek and B. Radovcic, Phys. Lett. B **687**, 338 (2010) [arXiv:0911.1374 [hep-ph]]; K. Kumericki, I. Picek and B. Radovcic, Phys. Rev. D **84**, 093002 (2011) [arXiv:1106.1069 [hep-ph]].

## 1 Введение Экспериментальные данные о массе нейтрино, полученные за последние десятилетия, являются конкретным доказательством физики, выходящей за пределы Стандартной модели (СМ) (см. например [1]). Хотя не удалось определить необходимые новые степени свободы, ясно, что скорее всего существуют дополнительные частицы, чтобы генерировать массы. Аналогично, существует обширное количество доказательств наличия дополнительного галактического компонента, неизвестного вещества, называемого тёмной материей (см. например [2]). Это может или не может требовать новых степеней свободы, но гипотеза о том, что тёмная материя состоит из стабильного (или долгоживущего) нового вида частиц, предоставляет простое объяснение этой наблюдаемой особенности Вселенной. Учитывая, что эти два показателя физики за пределами СМ могут быть объяснены расширением спектра частиц СМ, естественно задать вопрос, можно ли связать необходимые новые частицы. Может ли механизм образования массы нейтрино быть связанным с существованием стабильного кандидата на тёмную материю? Особенно простая модель, реализующая эту идею, была предложена Ма в 2006 году [3]. В этой модели основному набору Стандартной Модели добавляются дополнительный Стандартно-Модельный скалярный двойт и синглетные фермионы, которые все являются нечетными относительно дискретной симметрии \(Z_{2}\). Расширенный набор полей позволяет образованние радиационной массы нейтрино на однопетлевом уровне, в то время как самое легкое поле за пределами Стандартной Модели является абсолютно стабильным. Таким образом, получается простая синергетическая модель радиационной массы нейтрино и темной материи. В данной работе мы обобщаем подход Ма. Мы представляем класс связанных моделей, все они порождают массу нейтрино с помощью петляной диаграммы с той же топологией, что и у Ма, и при этом допускают стабильных кандидатов на тёмную материю. Петлевая диаграмма, используемая Ма, содержит вставку массы на внутренней фермионной линии (см. рисунок 1), и наши обобщения естественно подразделяются на две категории: те, которые нарушают симметрию лептонного числа путем вставки массы Майораны, и те с вставкой массы Дирака, при которой симметрия лептонного числа нарушается в вершине. Хотя базовый механизм очень похож в обоих случаях, эта разница модифицирует ожидания относительно содержимого полей за пределами Стандартной Модели и связанной феноменологии. Оказывается, что в обоих случаях этот подход очень общий и существует множество реализаций. Однако ограничение внимания на моделях, в которых мультиплеты внесмешенного типа не превышают представления адъюнктов, значительно сокращает возможности. Как мы увидим, существует только две такие (минимальные) модели с вставкой массы Майораны, которые уже известны [3, 4]. Мы находим семь дополнительных моделей с вставкой массы типа Дирака, все из которых обеспечивают радиационную массу нейтрино и кандидатов на темную материю. Мы подробно описываем эти модели, находим их подмножество, соответствующее прямому обнаружению экспериментов. Есть случаи с инертным синглетом, инертным дублетом и инертным триплетом; модели представляют естественную среду для инертных теорий \(N\)-tuplet темной материи, в которых также достигается радиационная масса нейтрино. Интересно, три из новых моделей предлагают простое расширение, которое может объяснить происхождение (ранее наложенной) дискретной симметрии. Путем повышения дискретной симметрии до калиброванной симметрии \(U(1)\) и расширения поля на одну синглетную скалярную частицу стандартной модели, дискретная симметрия может возникать как случайная симметрия лагранжиана низкоэнергетической области после нарушения симметрии \(U(1)\). Это предоставляет простое объяснение для дискретной симметрии. Хотя мы сосредотачиваемся на моделях с представлениями не большими, чем адъюнкт, мы также кратко рассматриваем случаи, когда дополнительные поля могут быть квадруплетной и/или квинтуплетной представлениями \(SU(2)_{L}\). Мы представляем кандидаты моделей в этих случаях и упоминаем некоторые ключевые вопросы, основываясь на уроках, извлеченных из наших предыдущих исследований. Несмотря на использование более крупных мультиплетов, эти модели всё равно могут быть интересными; помимо возможности возникновения радиационной массы нейтрино, экзотические частицы с более большими электрическими зарядами в этих мультиплетах могут повысить сигнал \(2\gamma\) и/или \(\gamma+Z\) от аннигиляции темной материи, когда они появляются в петлях [5]. Это может обеспечить простую связь между механизмом массы нейтрино и астрофизическим гамма-лучевым сигналом [6]. Перед тем, как продолжить, мы замечаем, что связь между радиационной массой нейтрино и темной материей была исследована в нескольких различных моделях, включая Ref. [7], предшествующую работу Ma; для других примеров см. [8]. Предыдущие работы по моделям с инертным синглетом [9], инертным двойником [10] и инертным тройником [11] также хорошо известны. Дополнительные соответствующие работы, занимающиеся инертной мультиплетной темной материей и/или радиационной массой нейтрино, приводятся в тексте. Также обратите внимание, что Refs. [12, 13] подробно описывают однопетлевые реализации оператора \(d=5\) для массы нейтрино. Инертная скалярная темная материя также может помочь устранить проблему малой иерархии, обнаруженную в низкомасштабных сисасах [14]. Настоящая работа основана на обобщенных сисасах на дереве уровня, представленных в Ref. [15]. План этой статьи следующий. В разделе 2 мы обсуждаем модель Ма и представляем обобщения, которые также обеспечивают радиационную массу нейтрино и кандидатов на тёмную материю. Раздел 3 рассматривает случай фермионной тёмной материи, в то время как раздел 4 обсуждает скалярную тёмную материю. Один из обобщённых моделей подробно представлен в разделе 5. В разделе 6 мы показываем, что некоторые модели позволяют простое расширение таким образом, что дискретная симметрия появляется как случайная симметрия в теории низких энергий. Модели с экзотиками, образующими более крупные представления \(SU(2)\), обсуждаются в разделе 7 (и явно приводятся в приложении). Мы заключаем в разделе 8. [FIGURE:S1.F1][ENDFIGURE] ## 2 Радиационная масса нейтрино и темная материя Мы интересуемся классом моделей, которые генерируют массу нейтрино радиативно по диаграмме на рисунке 1. Здесь \(\mathcal{F}\) является фермионом за пределами стандартной модели, а \(S_{1,2}\) являются новыми скалярами (которые могут быть идентичными в некоторых случаях). Особенностью этой диаграммы является то, что все три вершины могут включать два поля за пределами стандартной модели. В результате всегда можно рассмотреть дискретную симметрию \(Z_{2}\), действующую на полеты за пределами стандартной модели. \[\{\mathcal{F},\;S_{1},\;S_{2}\} \rightarrow -\ \{\mathcal{F},\;S_{1},\;S_{2}\}\;,\] (1) \[\{\mathcal{Ф},\;S_{1},\;S_{2}\} \rightarrow -\ \{\mathcal{Ф},\;S_{1},\;S_{2}\}\;,\] (1) Все поля SM преобразуются тривиально. Самое легкое поле внутри мультиплетов \(\mathcal{F}\) и \(S_{1,2}\) будет, следовательно, стабильным, и если это поле электрически нейтральное и безцветное, мы получаем кандидата на тёмную материю. Эти замечания являются общими для всех моделей данного типа; связь между массами петель и тёмной материей легко осознаваема в этом классе моделей. Фигура 1 представляет массы майоранских нейтрино, поэтому диаграмма петли должна содержать источник нарушения числа лептонов. Выбрав соглашение о симметрии числа лептонов таким образом, что новый фермион \(\mathcal{F}\) имеет то же значение, что и SM лептоны, существуют два способа явного нарушения симметрии числа лептонов; это может быть нарушено либо при массовой вставке, либо при одном из вершин. Самые простые модели в терминах требуемого количества мультиплетов за пределами SM - это модели с массовой вставкой, нарушающей численность лептонов (Майорановской). В этом случае \(\mathcal{F}_{L}\equiv\mathcal{F}_{R}^{c}\) и минимальные случаи возникают для \(S_{1}=S_{2}\equiv S\). Таким образом, требуется всего два мультиплета за пределами SM. Общая диаграмма петли для этого подмножества моделей приведена на рисунке 2. Сначала рассмотрим этот случай. ### Модели со вставкой массы Майораны Мы ищем модели, которые достигают массы нейтрино через Рисунок 2 и порождают кандидатов в тёмную материю. Чтобы позволить голую мажорановскую массу, фермион должен образовывать реальное представление калибровочной симметрии СМ, \(\mathcal{F}_{R}\sim(1,R_{\mathcal{F}},0)\). Поскольку мы рассматриваем кандидатов в тёмную материю, мы не рассматриваем цветные поля. Также обратите внимание, что \(R_{\mathcal{F}}\) должно быть нечётным, чтобы гарантировать отсутствие частиц с дробным зарядом (самая лёгкая из которых была бы стабильной и, следовательно, исключена космологически). Нечётное значение \(R_{\mathcal{F}}\) также обеспечивает наличие электрически нейтральной компоненты в \(\mathcal{F}_{R}\), поэтому эта требование не налагает дополнительных ограничений. С данной информацией можно получить пригодные комбинации \(\mathcal{F}_{R}\) и \(S\), которые генерируют Рисунок 2. Основными лагранжевыми терминами являются \[\mathcal{L} \supset i\bar{\mathcal{F}_{R}}\gamma^{\mu}D_{\mu}\mathcal{F}_{R}-\frac{M _{\mathcal{F}}}{2}\;\overline{\mathcal{F}_{R}^{c}}\mathcal{F}_{R}+|D^{\mu}S|^{2}-M_{S}^{2}|S|^{2}+\lambda\bar{L}\tilde{S}\mathcal{F}_{R}+\lambda_{\text{ \tiny SH}}(S^{\dagger}H)^{2}+\mathrm{H.c.},\] (2) где \(L\) (\(H\)) - это SM лептон (скалярный) двойник, а \(\tilde{S}\) обозначает сопряженно-заряженный \(S\). Оказывается, что возможные комбинации для \(\mathcal{F}\) и \(S\) не ограничены квантовыми числами; можно рассматривать все большие мультиплеты, предположительно, до некоторых единичных пределов [16], и реализовать модель с Рисунком 2 и кандидатом на темную материю. Однако, если мы ограничимся моделями с \(R_{\mathcal{F}},R_{S}\leq 3\), так что ни один новый мультиплет не будет больше сопряженного представления, то существует только два возможных варианта. Первый случай - это оригинальное предложение Ма, которое использует дополнительный (инертный) скалярный двойник \(S\sim(1,2,1)\) и фермион сингл Ма \(\mathcal{F}_{R}\sim(1,1,0)\)[3]. Эта модель является прототипом для класса, которым мы занимаемся. Вторая модель также использует скалярный двойник \(S\sim(1,2,1)\), но вместо этого использует тройной фермион \(\mathcal{F}_{R}\sim(1,3,0)\)[4], знакомый из Type-III seesaw [17]. Таким образом, обе модели известны в литературе, и нет дополнительных возможностей, если только не рассматриваются более крупные мультиплеты. В каждой из этих моделей кандидатом на роль тёмной материи может выступать нейтральная компонента S либо мажорановский фермион. Однако существует важное отличие между случаем синглета \(\mathcal{F}\sim(1,1,0)\) и другой моделью; синглет не участвует в слабых взаимодействиях и поэтому находится в термическом контакте с Стандартной моделью через юкавское связывание. В случае фермионной тёмной материи это может привести к конфликту между необходимостью сохранения большого юкавского связывания для обеспечения термической тёмной материи и необходимостью подавления юкавского связывания для ограничения размера эффектов, связанных с изменением вкуса. Такая проблема не возникает в модели фермионного триплета, так как фермионы могут поддерживать равновесие с Стандартной моделью через слабые взаимодействия в этих случаях, даже если юкавские связывания подавлены. Для анализа модели Ма с использованием последних данных LHC о бозоне Хиггса см., например, ссылку [18]. Также следует отметить, что петлевые эффекты могут вызывать наблюдаемые взаимодействия между тёмной материей и экспериментальными детекторами в модели Ма [19]. [FIGURE:S2.F2][ENDFIGURE] ### Модели с вставкой массы Дирака. После исчерпания минимальных моделей с нарушением числа лептонов через вставку массы, мы теперь рассматриваем модели с вставкой массы Дирака; то есть фермион за пределами СМ имеет ненулевую гиперзарядность. В этом случае общая массовая диаграмма имеет форму, показанную на рисунке 1. Поля \(\mathcal{F}_{R}\) и \(\mathcal{F}_{L}\) больше не связаны сопряжением зарядов, поэтому вставка массы является типом Дирака и \(\mathcal{F}\) является векторным фермионом. Кроме того, требуется \(S_{1}\neq S_{2}\). Мы снова рассматриваем симметрию \(Z_{2}\), при которой поля СМ преобразуются тривиально, но новые поля являются нечетными. Лагранжиан содержит следующие соответствующие члены: \[\mathcal{L} \supset i\bar{\mathcal{F}}\gamma^{\mu}D_{\mu}\mathcal{F}\ -\ M_{\mathcal {F}}\;\overline{\mathcal{F}}\mathcal{F}\ +\ \sum_{i=1,2}\left\{|D^{\mu}S_{i}|^ {2}\ -\ M_{i}^{2}|S_{i}|^{2}\right\}\] (3) \[+\ \lambda_{1}\;\bar{L}\mathcal{F}_{R}S_{1}\ +\ \lambda_{2}\;\bar {L}\mathcal{F}^{c}_{L}\tilde{S}_{2}\ +\ \lambda_{\text{\tiny SH}}\;S_{1}\tilde {S}_{2}H^{2}+\mathrm{H.c.},\] где, в нашей конвенции, симметрия числа лептонов нарушается юкавским связыванием. При присутствии симметрии \(Z_{2}\) нет членов в скалярном потенциале, линейных только в одном из новых скаляров \(S_{1,2}\). Таким образом, скаляры за пределами СМ не приобретают индуцированного ВЭБ и существует область параметров, для которой \(\langle S_{1,2}\rangle=0\), поэтому симметрия \(Z_{2}\) остается точной. При выборе пригодных множеств необходимо убедиться, что ни в одном из них нет поля с дробным зарядом, чтобы избежать (космологически исключенного) устойчивого заряженного поля. Чтобы гарантировать, что самое лёгкое Z2-нечётное поле является нейтральным кандидатом на роль тёмной материи, необходимо требовать, чтобы новые множества содержали хотя бы одно нейтральное поле. Обратите внимание, что нейтральное поле не обязательно должно появляться в виде явной пропагирующей степени свободы внутри диаграммы петли; достаточно лишь наличия диаграммы петли и содержания частиц, включающего нейтральное поле, которое может играть роль тёмной материи. С учетом этих условий мы ищем жизнеспособные комбинации мультиплетов за пределами Стандартной модели, которые реализуют Рисунок 1. Мы обнаруживаем, что размеры мультиплетов за пределами Стандартной модели не ограничены нашими требованиями; можно рассматривать все более крупные мультиплеты и реализовывать петлевую диаграмму. Однако, если обратить внимание только на модели, в которых ни один из мультиплетов за пределами Стандартной модели не больше адъюнктного представления, найдено только семь различных моделей. Они перечислены в Таблице 1. Из семи моделей, одна использует экзотический трехкратный лептон \(\mathcal{F}\sim(1,3,-2)\), изученный в работах [20, 21], три содержат экзотический векторный (и похожий на Стандартную модель) двойной лептон \(\mathcal{F}\sim(1,2,-1)\) [21, 22, 23], и две содержат заряженный двойной лептон \(\mathcal{F}\sim(1,2,-3)\) [21, 24]. Также есть модель с похожим на Стандартную модель заряженным синглетным фермионом, \(\mathcal{F}\sim(1,1,-2)\), который уже появился в работе [25]. Массы нейтрино принимают стандартную расчетную форму в этих моделях. Например, в моделях \((A)\) и \((B)\) только одиноко заряженные экзотические частицы распространяются в петле, а матрица масс нейтрино СМ задается³ [FOOTNOTE:3][ENDFOOTNOTE] перевести маркдаун с английского на русский. Сохранить формулы: \[(\mathcal{M}_{\nu})_{\alpha\beta} \simeq \frac{\left[(\lambda_{2}^{*})^{a}_{\alpha}(\lambda_{1}^{*})^{a}_{ \beta}+(\lambda_{2}^{*})^{a}_{\beta}(\lambda_{1}^{*})^{a}_{\alpha}\right]}{32 \pi^{2}}\,\frac{\lambda_{\text{\tiny SH}}\langle H\rangle^{2}}{M_{>}^{2}-M_{<} ^{2}}\left[\frac{M^{2}_{>}\,M_{\mathcal{F},a}}{M_{\mathcal{F},a}^{2}-M_{>}^{2} }\,\log\frac{M_{\mathcal{F},a}^{2}}{M_{>}^{2}}\ -\ (M_{>}\to M_{<})\right]\] Здесь \(M_{\mathcal{F},a}\) - это масса заряженной компоненты экзотического фермиона \(\mathcal{F}_{a}\), и подразумевается суммирование по повторяющемуся индексу \(a\) (который обозначает поколения экзотических фермионов).⁴ Массы \(M_{>,<}\) относятся к массовым собственным состояниям заряженных скалярных частиц, которые являются линейными комбинациями заряженных скаляров \(S_{1}^{+}\) и \(S_{2}^{+}\). Смешивание происходит из-за члена \(\lambda_{\text{\tiny SH}}\)-терма в уравнении (3), который принимает явный вид \(\lambda_{\text{\tiny SH}}\tilde{H}^{\dagger}S_{1}S_{2}^{\dagger}H\subset \mathcal{L}\) для моделей \((A)\) и \((B)\). Если все экзотики находятся на тевтонском масштабе, то для получения \(m_{\nu}\sim 0.1\) эВ требуются безразмерные связи порядка \(\mathcal{O}(10^{-3})\). Сценарий, в котором все экзотики находятся на тевтонском масштабе, наиболее интересен с феноменологической точки зрения. Однако строго говоря, чтобы получить кандидата на тёмную материю, достаточно, чтобы у самой лёгкой экзотики была масса порядка \(\lesssim\mathcal{O}(\mathrm{TeV})\). Остальные экзотики могут быть значительно тяжелее, что позволяет большим безразмерным связям. [FOOTNOTE:4][ENDFOOTNOTE] - [Сноска:4][КОНЕЦ СНОСКА] Перед тем, как перейти к более подробному обсуждению темной материи, отметим, что модели (A), (B) и (D) из таблицы 1, ожидается, что они порождают (доминирующие) радиационные массы нейтрино в отсутствие симметрии \(Z_{2}\), о чем мы кратко обсудим в Приложении A. [TABLE:S2.T1][ENDTABLE] ## 3 Инертная фермионная тёмная материя Теперь обратим внимание на кандидатов на темную материю в этих моделях. _А преори_ возможно, что и фермионные, и скалярные кандидаты на темную материю возможны, как в исходном предложении Ма [3]. В этом разделе мы рассмотрим фермионную темную материю. Обратите внимание, что не все модели содержат нейтральные фермионы за пределами Стандартной Модели; конкретно, модель \((A)\) имеет \(\mathcal{F}\sim(1,1,-2)\), а модели \((F)\) и \((G)\) используют \(\mathcal{F}\sim(1,2,-3)\). В этих случаях все фермионы за пределами Стандартной Модели заряжены, и возможна только скалярная темная материя. В этих моделях уже можно исключить пространство параметров с легкими фермионами, а именно \(M_{\mathcal{F}}<M_{1,2}\), из-за появления стабильного заряженного фермиона. С другой стороны, модели (B) через (E) все содержат нейтральные фермионы и, в принципе, могут принимать фермионную темную материю. Однако у всех фермионных мультиплетов в этих моделях ненулевая гиперзарядность, что может привести к сильным ограничениям от экспериментов прямого детектирования. Более точно, если изобилие темной материи порождается стандартной термической WIMP-частицей, то можно исключить дираковскую фермионную темную материю с ненулевой гиперзарядностью из-за сильных ограничений, например, от XENON100 [26]. Таким образом, важно определить, является ли нейтральный фермион дираковым или майорановским. На дереве уровня фермион \(\mathcal{F}\) остается Дираковской частицей. Однако его связь с нейтрино Стандартной Модели, которые получают Майорановкие массы через фигурку 1, приводит к небольшой радиационной Майорановской массе. В случае \(\mathcal{F}\sim(1,3,-2)\), типичная диаграмма показана на рисунке 3. Аналогичные диаграммы могут возникать для моделей (C) до (E), хотя в этих случаях скаляр \(S_{1}\) является вещественным. Луп-индуцированная Майорановская масса, в общем случае, расщепляет дираковский фермион \(\mathcal{F}\) на пару Майорановских фермионов. Однако можно уже видеть, что расщепление массы будет очень малым. Подлупа, показанная на рисунке 3, является той же самой луп-диаграммой, которая порождает массы нейтрино Стандартной Модели на рисунке 1. Таким образом, в пределе, когда массы нейтрино Стандартной Модели исчезают, \(m_{\nu}\to 0\), Майорановская масса для \(\mathcal{F}\) также исчезает. Поэтому мы ожидаем \(\Delta M_{\mathcal{F}}\propto m_{\nu}\), где \(\Delta M_{\mathcal{F}}\) - это Майорановская масса для \(\mathcal{F}\). Это подтверждается явными вычислениями. Например, при \(M_{\mathcal{F}}\ll M_{S}\), где \(M_{S}\) обозначает приблизительно одинаковую массу за пределами-Стандартной Модели скаляров, получается \[\Delta M_{\mathcal{F}} \sim \frac{\lambda_{1}^{2}\lambda_{11\text{\tiny H}}}{16\pi^{2}}\, \frac{\langle H\rangle^{2}}{M_{S}^{2}}\times m_{\nu},\] (5) где Лагранжиан содержит термин \(\lambda_{11\text{\tiny H}}^{*}(H^{\dagger}S_{1})^{2}\subset\mathcal{L}\) для генерации верхнего вершины на Рис. 3. Вне-стандартные нейтральные фермионы, следовательно, образуют псевдо-Дираковы частицы с маленьким расщеплением. [ФИГУРА:S3.F3][КОНЕЦФИГУРЫ] Эксперименты прямого обнаружения серьезно ограничивают упругое рассеяние безучастных осей, которое может происходить, когда фермионная темная материя связывается с бозоном \(Z\) [26]. Эти ограничения можно избежать, если фермион Дирака имеет разделение масс, поскольку полученная пара мажорановых фермионов имеет недиагональные связи с бозоном \(Z\) (ведущего порядка). При условии, что разделение масс превышает среднюю кинетическую энергию местных частиц темной материи, обменом бозоном \(Z\) с детекторами стандартной модели сильно подавляется, поскольку тяжелый фермион кинематически недоступен. Однако для моделей с нейтральными фермионами из таблицы 1 разделение масс удовлетворяет уравнению \[\frac{\Delta M_{\mathcal{F}}}{M_{\mathcal{F}}} < \frac{m_{\nu}}{M_{\mathcal{F}}}\ \ \lesssim\ \ 10^{-12}\quad\quad \mathrm{для}\quad M_{\mathcal{F}}=\mathcal{O}(\mathrm{TeV}),\] (6) который слишком мал, чтобы избежать прямых границ обнаружения, с учетом типичных скоростей темной материи \(v_{\text{\tiny DM}}\sim 10^{-3}\). Мы приходим к выводу, что ни одна из моделей в Таблице 1 не является приемлемой, когда наименьшее поле за пределами СМ является фермионом, из-за либо космологически исключенной стабильной заряженной частицы, либо кандидата на темную материю, противоречащего прямым ограничениям обнаружения. Весь регион параметров, в котором фермион является наименьшим состоянием за пределами СМ, тем самым исключен для этих моделей. ## 4 Инертная скалярная тёмная материя С учетом вышеуказанной информации мы можем ограничить наше внимание пределом \(M_{\mathcal{F}}\gg M_{1,2}\) для моделей, представленных в таблице 1, в которых стабильная частица является скалярной. В этом пределе модели эффективно являются моделями инертных \(N\)-метюль, с дополнительной особенностью реализации радиоактивной массы нейтрино. В этом разделе мы рассмотрим жизнеспособность кандидатов в скалярную темную материю в разных моделях. Сначала мы рассмотрим модели \((А)\) и \((В)\), у которых общие особенности позволяют их обсуждать вместе. Обе эти модели имеют единственный (кандидатный) множественный темный материал, который является инертным скалярным двойником, \(S_{1}\sim(1,2,1)\); то есть инертный двойник [10]. Также в обеих моделях второй скаляр является заряженным двойником, \(S_{2}=(S_{2}^{++},S_{2}^{+})^{T}\), компоненты которого должны быть тяжелее темного материала. Инертный двойник темного материала хорошо изучен в литературе, и известно, что может быть достигнуто приемлемое количество темного материала [10]. Инертный двойник приводит к трем новым скалярам, которые мы обозначаем как \(H^{\prime\pm}\), \(H^{\prime 0}\) и \(A^{0}\), и любые из последних двух могут быть темным материалом. Как и обычно для модели инертного двойника, нейтральные компоненты \(S_{1}\) не могут смешиваться с СМ-гиггсом в моделях \((А)\) и \((В)\) из-за дискретной симметрии. Однако заряженный скаляр \(S_{1}^{+}\) будет смешиваться с \(S_{2}^{+}\), как уже упоминалось. Если это смешивание большое, то феноменология самого лёгкого заряженного скаляра будет отличаться от \(H^{\prime+}\) в стандартной модели инертного двойника. При малом смешивании самый лёгкий заряженный скаляр в основном будет соответствовать \(H^{\prime+}\), и феноменология \(S_{1}\) будет хорошо аппроксимироваться стандартной моделью инертного двойника. Обратите внимание, что нельзя взять предел \(\lambda_{\text{\tiny SH}}\to 0\) без выключения радиационной массы нейтрино на Рис. 1. Требование, чтобы радиационная масса нейтрино была реализована, поэтому требует ненулевого смешивания между \(S_{1}^{+}\) и \(S_{2}^{+}\). Однако, учитывая, что \(S_{2}\) должен быть тяжелее тёмного материала, можно ожидать, что смешивание будет порядка \(\langle H^{0}\rangle^{2}/M_{2}^{2}\), которое для \(M_{2}\gtrsim\) ТэВ равно или меньше \(10^{-1}\). Таким образом, \(S_{1}\) может быть хорошо аппроксимирован стандартной моделью инертного двойника. Модель инертного двойника содержит пять основных областей параметров, в которых наблюдается реликтовая плотность [27]. В четырех из них спектр легких частиц может быть исследован на Большом адронном коллайдере. Обнаружение скалярного частицы, похожей на стандартную модель, с массой около \(125\) ГэВ на Большом адронном коллайдере позволяет обновить пригодное пространство параметров и феноменологию моделей инертного двойника. Недавний анализ, основанный на данных Большого адронного коллайдера, показывает, что области низкой массы для кандидатов в тёмную материю уже могут испытывать напряжение из-за ограничений от XENON100 [26] и WMAP [28], тогда как более тяжелая область с \(M_{\text{\tiny DM}}\gtrsim 500\) ГэВ по сути не затронута [29]. Конкретно, выживающая область для более легкой тёмной материи находится близко к резонансу Хиггса/порогу производства \(WW\) [29]. Область пространства параметров с \(M_{\text{\tiny DM}}=\mathcal{O}(10)\) ГэВ является особенно интересной для представленных моделей, поскольку, в этом случае, дополнительные множества за пределами СМ могут быть достаточно легкими для появления на Большом адронном коллайдере (LHC). Это уже обсуждалось в работе [25] для модели \((A)\), где показано, что заряженное скалярное двойноеt \(S_{2}\sim(1,2,3)\) может порождать наблюдаемые сигналы, когда холодное темное вещество инертного двойника является легким. Хотя область пространства параметров с более тяжелым темным веществом (\(M_{\text{\tiny DM}}\gtrsim 500\) ГэВ) не будет доступна на Большом адронном коллайдере (LHC), ожидается, что XENON-1T будет исследовать эту область параметров, потенциально предоставляя наблюдаемые сигналы прямого обнаружения [30]. Отсюда следует, что жизнеспособное темное вещество возможно как в моделях \((A)\), так и в \((B)\), и ожидается, что комбинированные (проекционные) данные LHC и XENON-1T будут исследовать жизнеспособное пространство параметров в этих моделях. Мы отмечаем, что в общем случае модели с темной материей без гиперзаряда не так сильно ограничены экспериментами по прямому обнаружению. Такие кандидаты не связаны напрямую с бозоном Z, поэтому взаимодействия с детекторами не возникают на уровне дерева. При условии, что разделение массы между заряженными и нейтральными компонентами мультиплета темной материи превышает среднюю кинетическую энергию темной материи в локальном гало, взаимодействия с бозоном W также сильно подавлены (или отсутствуют). Даже если нейтральные и заряженные компоненты мультиплета темной материи в силу дерева являются вырожденными, через обмен бозоном W индуцируется радиативное разделение порядка 100 МэВ, что достаточно для подавления / отсутствия рассеяния через обмен бозоном W. Эти комментарии относятся к модели \((D)\), в которой единственным кандидатом на роль темной материи является нейтральный компонент инертного реального трехкратного скалярного поля \(S_{1}\sim(1,3,0)\). Нейтральный компонент этой кратности не взаимодействует с бозоном \(Z\), а заряженный компонент может быть достаточно рассщеплен (радиационными эффектами), чтобы гарантировать, что нейтральное состояние является самым легким полем. Это уменьшает потенциальное противоречие с экспериментами по прямому обнаружению. Возможность инертного трехкратного скрытого скалярного поля в качестве темной материи хорошо известна в литературе [11, 31, 32, 33]. Нейтральный компонент \(S_{1}\) является жизнеспособным кандидатом на роль холодной темной материи, насыщающим наблюдаемую остаточную плотность \(\Omega_{\text{\tiny CDM}}\hat{h}^{2}\simeq 0.11\)[28] для \(M_{\text{\tiny DM}}\approx 2.5\) ТэВ [11]. Если трехкратное скрытое скалярное поле будет легче, то оно может составлять только часть общего объема темной материи, и потребуются дополнительные кандидаты. В модели \((D)\) объем темной материи должен состоять исключительно из \(S_{1}\), поэтому \(M_{\text{\tiny DM}}\approx 2.5\) ТэВ является необходимым условием для этой модели. К сожалению, это затрудняет прямое производство экзотических состояний на Большом адронном коллайдере (ЛАА); как \(\mathcal{F}\sim(1,2,-1)\), так и \(S_{2}\sim(1,1,2)\) должны быть тяжелее \(2.5\) ТэВ, чтобы гарантировать, что темная материя является самым легким экзотическим состоянием, выходящим за пределы предполагаемого экспериментального достижения. Однако модель \((D)\) является жизнеспособной моделью темной материи и радиационного массы нейтрино при \(M_{\text{\tiny DM}}\approx 2.5\) ТэВ. Затем мы обращаем свое внимание на модели \((F)\) и \((G)\), которые оба используют \(\mathcal{F}\sim(1,2,-3)\) и \(S_{1}\sim(1,3,2)\). В обоих моделях \(S_{2}\) состоит исключительно из электрически заряженных полей, поэтому нейтральная компонента \(S_{1}\) является единственным кандидатом в темную материю. Это комплексное нейтральное поле не может смешиваться с скалярным полем Стандартной Модели из-за симметрии \(Z_{2}\), поэтому его частицы и античастицы остаются вырожденными. Поэтому количество темной материи включает оба состояния, что представляет серьезную сложность для этих моделей. Из-за ненулевого гиперзаряда для \(S_{1}\) нейтральное поле может рассеиваться на детекторах Стандартной Модели через обмен \(\Z\)-бозоном на дереве. Этот процесс сильно ограничен данными непосредственного обнаружения. Предыдущие работы показывают, что для получения правильного количества темной материи требуется масса примерно \(2.6\) ТэВ, однако, спин-независимое сечение превышает \(10^{-37}\) см\({}^{2}\) в областях параметров, совместимых с экспериментами на LEP [32, 33]. Такое большое сечение несовместимо с ограничениями, например, от XENON100 [26]. Таким образом, хотя можно успешно получить необходимое количество темной материи, ограничения на непосредственное обнаружение оказываются фатальными для моделей \((F)\) и \((G)\), и обе модели могут быть исключены. Остается рассмотреть модели \((C)\) и \((E)\). Эти модели допускают два различных скалярных кандидата на темную материю и, следовательно, позволяют больше возможностей, как мы увидим в следующем разделе. ## 5 Моделей с вещественным скаляром и комплексным триплетом Модели \((C)\) и \((E)\) оба используют SM-подобные фермионы \(\mathcal{F}\sim(1,2,-1)\) и комплексный скалярный трехплет \(S_{2}\sim(1,3,2)\). Кроме того, в обоих случаях \(S_{1}\) является вещественным скаляром. Эти модели отличаются от других случаев тем, что оба скаляра теперь имеют нейтральную компоненту, что дает двух кандидатов на темную материю. Мы видели, что модели \((F)\) и \((G)\) могут быть исключены именно потому, что обилие темной материи состояло из нейтральной компоненты комплексного скалярного трехплета. Однако, эта сложность устраняется в моделях \((C)\) и \((E)\) благодаря разрешенному массовому смешиванию между нейтральными компонентами \(S_{1}\) и \(S_{2}\). В этом разделе мы более подробно рассмотрим модель \((C)\), чтобы прояснить возможности. Анализ модели \((E)\) достаточно похож на эту, из-за связанных фермионных компонентов, и мы ограничимся краткими комментариями по этой модели в конце раздела. Модель (C) содержит скаляры за пределами Стандартной Модели \(S_{1}\sim(1,1,0)\equiv S\) и \(S_{2}\sim(1,3,2)\equiv\Delta\). Полный потенциал скаляров может быть записан как \[V(H,S,\Delta) = \frac{-\mu^{2}}{2}|H|^{2}+\frac{\tilde{M}_{S}^{2}}{2}S^{2}+\tilde {M}_{\Delta}^{2}\mathrm{Tr}(\Delta^{\dagger}\Delta)+\lambda_{1}|H|^{4}+\lambda _{2}\,[\mathrm{Tr}(\Delta^{\dagger}\Delta)]^{2}\] (7) \[+\lambda_{2}^{\prime}\,\mathrm{Tr}(\Delta^{\dagger}\Delta\Delta^{ \dagger}\Delta)+\frac{\lambda_{3}}{2}S^{4}+\lambda_{4}\,|H|^{2}\,\mathrm{Tr}( \Delta^{\dagger}\Delta)+\lambda_{4}^{\prime}\,H^{\dagger}\Delta^{\dagger}\Delta H\] \[+\lambda_{5}|H|^{2}S^{2}+\lambda_{6}\,S^{2}\,\mathrm{Tr}(\Delta^{ \dagger}\Delta)+\lambda_{\text{\tiny SH}}S\left\{\tilde{H}^{\dagger}\Delta^{ \dagger}H+H^{\dagger}\Delta\tilde{H}\right\},\] где общая фаза \(\Delta\) использовалась для выбора \(\lambda_{\text{\tiny SH}}\) вещественным без потери общности.⁵ Дискретная симметрия \(\{S,\,\Delta\}\rightarrow-\{S,\,\Delta\}\) гарантирует отсутствие смешивания масс между скалярными полями СМ и полями за пределами СМ. Эта симметрия также запрещает линейные термы с одним полем за пределами СМ, такие как \(H\Delta^{\dagger}H\) или \(SH^{2}\), которые в противном случае вызывали бы ненулевую ВЭД для \(\Delta\) и \(S\) после нарушения электрослабой симметрии. Следовательно, существует параметрическое пространство, в котором ни \(S\), ни \(\Delta\) не приобретают ВЭД. Однако скаляр \(S\) и нейтральные компоненты \(\Delta\) будут смешиваться в результате члена \(\lambda_{\text{\tiny SH}}\) в потенциале. [СИМВОЛ3:5][КОНЕЦСИМВОЛА] Раскрывая нейтральный SM-скаляр вокруг его VEV и раскрывая нейтральную компоненту \(\Delta\) как \[H^{0}=\frac{1}{\sqrt{2}}(v+h^{0}+i\chi^{0})\quad\mathrm{и} \quad\Delta^{0}=\frac{1}{\sqrt{2}}(\Delta_{R}+i\Delta_{I}),\] (8) соответственно, массово-смешивающий лагранжиан для нейтральных скаляров записывается в виде \[ \mathcal{L} \supset -\frac{1}{2}\mathcal{S}^{T}\mathcal{M}^{2}\mathcal{S}. \] (9) \[\mathcal{L} \supset -\frac{1}{2}\mathcal{S}^{T}\mathcal{M}^{2}\mathcal{S}.\] (9) Здесь базисный вектор представлен в виде \(\mathcal{S}=(S,\Delta_{R},\Delta_{I})^{T}\), и матрица квадрат-масс имеет следующую форму \[\mathcal{M}^{2}=\left(\begin{array}[]{ccc}\hidden@noalign{}\hfil \tilde{M}_{S}^{2}+\lambda_{5}v^{2}&\frac{\lambda_{\text{\tiny SH}}}{2\sqrt{2}} v^{2}&0\\ \hidden@noalign{}\hfil\frac{\lambda_{\text{\tiny SH}}}{2\sqrt{2}}v^{2}&\tilde{ M}_{\Delta}^{2}+\frac{\lambda_{4}}{2}v^{2}&0\\ \hidden@noalign{}\hfil 0&0&\tilde{M}_{\Delta}^{2}+\frac{\lambda_{4}}{2}v^{2} \end{array}\right).\] (13) Таким образом, CP-нечетный скаляр \(\Delta_{I}\) является собственным состоянием с массой \(\tilde{M}_{\Delta}^{2}+\lambda_{4}v^{2}/2\), в то время как CP-четные скаляры \(S\) и \(\Delta_{R}\) масс-смешиваются, образуя два физических скаляра, которые являются линейными комбинациями этих полей. Предполагаемым кандидатом на темную материю будет одно из собственных состояний масс нейтрального скаляра. Чтобы определить, какое именно состояние, нам необходимо найти массы для смешанных CP-четных состояний. Давайте определим \(M_{S}^{2}=\tilde{M}_{S}^{2}+\lambda_{5}v^{2}\) и \(M^{2}_{\Delta}=\tilde{M}_{\Delta}^{2}+\lambda_{4}v^{2}/2\), которые являются массовыми состояниями CP-четных частиц в пределе \(\lambda_{\text{\tiny SH}}\to 0\). В этом пределе \(\Delta_{R}\) и \(\Delta_{I}\) являются вырожденными и образуют одну комплексную скалярную частицу с массой \(M^{2}_{\Delta}\). При ненулевом значении \(\lambda_{\text{\tiny SH}}\) значения массовых состояний CP-четных частиц могут быть записаны как \[M_{\pm}=\frac{1}{2}\left\{M_{S}^{2}+M^{2}_{\Delta}\pm\left[(M_{S }^{2}-M^{2}_{\Delta})^{2}+\frac{\lambda_{\text{\tiny SH}}^{2}}{2}v^{4}\right]^ {1/2}\right\},\] (14) где собственные состояния связаны с исходными полями как \[\left(\begin{array}[]{c}\hidden@noalign{}\hfil S_{+}\\ \hidden@noalign{}\hfil S_{-}\end{array}\right)=\left(\begin{array}[]{cc} \hidden@noalign{}\hfil\cos\theta&\sin\theta\\ \hidden@noalign{}\hfil-\sin\theta&\cos\theta\end{array}\right)\,\left(\begin{ array}[]{c}\hidden@noalign{}\hfil S\\ \hidden@noalign{}\hfil\Delta_{R}\end{array}\right).\] (21) translated into Russian. Equations are preserved in their original form. Здесь угол смешивания сохраняется в оригинальной форме уравнений. \[\tan 2\theta = \frac{\lambda_{\text{\tiny SH}}v^{2}}{\sqrt{2}(M^{2}_{S}-M^{2}_{ \Delta})}.\] (22) translates to: \[\tan 2\theta = \frac{\lambda_{\text{\tiny SH}}v^{2}}{\sqrt{2}(M^{2}_{S}-M^{2}_{ \Delta})}.\] (22) В пределе, когда скалярный синглет является самым тяжелым, \(M_{S}^{2}\gg M^{2}_{\Delta}\), собственные значения масс примерно равны. \[M_{+}^{2}\simeq M_{S}^{2}+\frac{\lambda_{\text{\tiny SH}}^{2}v^{ 4}}{8M_{S}^{2}}\quad\mathrm{и}\quad M_{-}^{2}\simeq M^{2}_{\Delta}-\frac{ \lambda_{\text{\tiny SH}}^{2}v^{4}}{8M_{S}^{2}}\quad\mathrm{для}\quad M_{S}^{2 }\gg M^{2}_{\Delta}.\] (23) Обратим внимание, что \(M_{-}^{2}<M^{2}_{\Delta}\), что позволяет заключить, что \(S_{-}\) является самым лёгким экзотическим состоянием и, следовательно, кандидатом на тёмную материю. Простые выражения могут быть получены для собственных векторов масс в этом пределе: \[\left.\begin{array}[]{c}\hidden@noalign{}\hfil S_{+}\simeq S+ \frac{\lambda_{\text{\tiny SH}}v^{2}}{2\sqrt{2}M_{S}^{2}}\Delta_{R}\\ \\ \hidden@noalign{}\hfil S_{-}\simeq\Delta_{R}-\frac{\lambda_{\text{\tiny SH}}v^ {2}}{2\sqrt{2}M_{S}^{2}}S\end{array}\right.\quad\quad\mathrm{для}\quad M_{S}^{ 2}\gg M^{2}_{\Delta},\] (27) таким образом, самая легкая скалярная частица \(S_{-}\) в основном состоит из \(\Delta_{R}\). Таким образом, для \(M_{S}^{2}\gg M^{2}_{\Delta}\) темная материя состоит из \(S_{-}\), которая в основном состоит из четной части (\(\Delta_{R}\)) нейтрального поля скалярного трехпроекционного \(S_{2}\). Массовое разделение между \(S_{-}\) и состоянием с нечетной частью \(\Delta_{I}\) составляет \(|\Delta M^{2}|=\lambda_{\text{\tiny SH}}^{2}v^{4}/8M_{S}^{2}\). При условии, что это разделение превышает кинетическую энергию темной материи, \(\sqrt{|\Delta M^{2}|}>\mathrm{KE}_{\text{\tiny DM}}\), состояние \(\Delta_{I}\) не будет доступно кинематически через процессы на деревянном уровне в экспериментах по прямому обнаружению. Это значительно ослабляет ограничения на темную материю, возникающие из сложного трехпроекционного скаляра. Это также дает верхнюю границу на параметр массы \(M_{S}^{2}\), после которой разделение между темной материей и \(\Delta_{I}\) настолько мало, что ожидается рассеяние на деревьях через обмен \(Z\) в экспериментах на современном уровне. Однако обнаруживается \[M_{S} < \frac{1}{2\sqrt{2}}\,\frac{|\lambda_{\text{\tiny SH}}|\,v^{2}}{ \mathrm{KE}_{\text{\tiny DM}}}\ \simeq\ \left(\frac{|\lambda_{\text{\tiny SH}} |}{10^{-2}}\right)\,\left(\frac{10^{-3}}{v_{\text{\tiny DM}}}\right)^{2}\left( \frac{2.6~{}\mathrm{TeV}}{M_{\text{\tiny DM}}}\right)\times 10^{2}~{}\mathrm{ TeV}.\] (28) \[ M_{S} < \frac{1}{2\sqrt{2}}\,\frac{|\lambda_{\text{\tiny SH}}|\,v^{2}}{ \mathrm{KE}_{\text{\tiny DM}}}\ \simeq\ \left(\frac{|\lambda_{\text{\tiny SH}} |}{10^{-2}}\right)\,\left(\frac{10^{-3}}{v_{\text{\tiny DM}}}\right)^{2}\left( \frac{2.6~{}\mathrm{TeV}}{M_{\text{\tiny DM}}}\right)\times 10^{2}~{}\mathrm{ TeV}.\] (28) Таким образом, более тяжелое состояние \(S_{+}\) не может быть произвольно сделано тяжелым, если темная материя должна избежать исключения через, например, данные XENON100. С \(\ M_{\text{\tiny DM}}\equiv M_{-}=\mathcal{O}(\mathrm{TeV})\), разность масс между \(S_{-}\) и \(\Delta_{I}\) меньше, чем \(M_{\Delta}\) (масса \(\Delta_{I}\)). Когда температура падает ниже \(M_{\Delta}\), более тяжелое состояние \(\Delta_{I}\) распадается, и распадные продукты обязательно содержат \(S_{-}\) из-за сохраняющейся дискретной симметрии. Выражение \(|\Delta M^{2}|=\lambda_{\text{\tiny SH}}^{2}v^{4}/8M_{S}^{2}\) показывает, что разность масс между \(S_{-}\) и \(\Delta_{I}\) ограничена как \(\sqrt{|\Delta M^{2}|}\lesssim|\lambda_{\text{\tiny SH}}|\times 4\) ГэВ, учитывая, что для достижения правильного остаточного изобилия требуется \(M_{\Delta}\gtrsim 3\) ТэВ, и мы работаем с \(M_{S}>M_{\Delta}\). В этом диапазоне масс \(\Delta_{I}\) может распадаться как \(\Delta_{I}\to S_{-}+Z^{*}\to S_{-}+\bar{f}f\), где \(f\) является фермионом СМ с массой \(m_{f}<|\lambda_{\text{\tiny SH}}|\times 2\) ГэВ. Поэтому, даже если заряженные фермионы СМ кинематически недоступны, конечное состояние, содержащее нейтрино, будет доступно, если только \(\lambda_{\text{\tiny SH}}\) является исключительно малым. После того, как \(\Delta_{I}\) распадется, адронный плазма состоит из \(S_{-}\) и полей СМ. \(S_{-}\) может поддерживать равновесие с сектором СМ через взаимодействия калибровочных полей и через квартетные члены \(\lambda_{4}\) и \(\lambda_{4}^{\prime}\) (в дальнейшем \(\lambda_{4}\)) в уравнении (7).⁶ Когда квартовые взаимодействия преобладают, модель похожа на модель инертного реального трехлинейного поля; изобилие темной материи будет получено при \(M_{\text{\tiny DM}}\simeq 2.5\) ТэВ, в соответствии с анализом Ref. [11]. При уменьшении \(\lambda_{4}\), разность масс на дереве между заряженными и нейтральными компонентами \(\Delta\) уменьшается, и становятся доступными каналы коаннигиляции, такие как \(\Delta^{-}\Delta^{++}\to W^{+}\gamma\). В этот момент, уменьшение \(\lambda_{4}\) не изменяет необходимую массу темной материи, так как калибровочные взаимодействия преобладают. Анализ Ref. [33] модели инертного комплексного трехлинейного поля показывает, что требуется \(M_{\text{\tiny DM}}\gtrsim 2.8\) ТэВ для всего диапазона параметров.⁷ Мы предполагаем, что \(M_{\text{\tiny DM}}\gtrsim 2.5\) ТэВ будет необходимо даже при преобладании калибровочных взаимодействий над квартовыми взаимодействиями во время фризаута для данной ситуации. При этом значении модель \((C)\) становится жизнеспособной моделью массы нейтрино и темной материи. Однако будет сложно создать экзотики в этой модели, учитывая, что самая легкая масса экзотики составляет \(\gtrsim 2.5\) ТэВ.⁸ [СНОСКА:6][КОНЕЦ СНОСКИ] [ССЫЛКА:7][КОНЕЦ_ССЫЛКИ] [FOOTNOTE:8][ENDFOOTNOTE] - Требуется сохранить формулы. Мы теперь кратко обсудим альтернативный предел с \(M_{S}^{2}\ll M^{2}_{\Delta}\). В этом случае собственные массы для четных ЦП-состояний равны \[M_{+}^{2}\simeq M_{\Delta}^{2}+\frac{\lambda_{\text{\tiny SH}}^{ 2}v^{4}}{8M_{\Delta}^{2}}\quad\mathrm{и}\quad M_{-}^{2}\simeq M^{2}_{S}- \frac{\lambda_{\text{\tiny SH}}^{2}v^{4}}{8M_{\Delta}^{2}}\quad\mathrm{для} \quad M_{\Delta}^{2}\gg M^{2}_{S}.\] (29) Мы видим, что кандидат на темную материю остается самым легким собственным состоянием \(S_{-}\) с четной зарядовостью \(CP\), массой \(M_{-}\). Теперь массовые собственные состояния представляют собой \[\left.\begin{array}[]{c}\hidden@noalign{}\hfil S_{+}\simeq\Delta_ {R}+\frac{\lambda_{\text{\tiny SH}}v^{2}}{2\sqrt{2}M_{\Delta}^{2}}S\\ \\ \hidden@noalign{}\hfil S_{-}\simeq S-\frac{\lambda_{\text{\tiny SH}}v^{2}}{2 \sqrt{2}M_{\Delta}^{2}}\Delta_{R}\end{array}\right.\quad\quad\mathrm{для}\quad M _{\Delta}^{2}\gg M^{2}_{S},\] (33) таким образом, большая часть тёмной материи состоит в основном из синглет-скаляра \(S\). Синглет-скалярная тёмная материя хорошо известна [9], и подробный анализ показывает, что \(M_{\text{\tiny DM}}\gtrsim 80\) ГэВ совместима с ограничениями на непосредственное обнаружение и данными WMAP для массы Хиггса \(m_{h}\simeq 125\) ГэВ [37]. Пригодная область параметров может быть исследована с помощью XENON1T, за исключением небольшого резонансного окна с \(M_{\text{\tiny DM}}\simeq 62\) ГэВ, где связь между тёмной материей и Хиггсом может быть очень слабой. Более лёгкая тёмная материя с \(M_{\text{\tiny DM}}\lesssim 60\) ГэВ отвергается ограничениями LHC на наблюдаемый распад Хиггса [37]. Мы видим, что модель (С) имеет жизнеспособное пространство параметров, в котором она ведет себя как модель инертного трехкомпонентного состояния или модель инертного синглета. Этот анализ достаточен, чтобы показать, что у модели (Е) также есть жизнеспособные области пространства параметров. В модели (Е) первый скаляр имеет вид \(S_1 \sim (1,3,0)\), в то время как второй скаляр остается \(S_2 \sim (1,3,2)\). Скалярный потенциал для этой модели содержит член, аналогичный члену \(\lambda_{\text{\tiny SH}}\) в уравнении (7), который смешивает нейтральную компоненту \(S_1\) с CP-четной нейтральной компонентой \(S_2\). Если \(S_2\) является самым тяжелым, модель ведет себя как модель инертного вещественного трехкомпонентного состояния, в то время как если \(S_1\) является самым тяжелым, самый легкий скаляр в основном состоит из \(\Delta_R\) (нейтральная CP-четная часть \(S_2\)). Ограничения на прямое обнаружение могут быть обойдены из-за массового смешивания, и модель снова является эффективной моделью инертного трехкомпонентного темного вещества. В обоих случаях мы ожидаем, что достижимая плотность темного вещества и достижимые массы нейтрино могут быть получены, хотя темное вещество будет тяжелым, с \(M_{\text{\tiny DM}}\gtrsim 2.5\) ТэВ (не учитывая резонансные области). Определение перспектив наблюдений для мультиплетов за пределами Стандартной Модели на Большом Адронном Коллайдере (ЛАК) с использованием ограничения \(M_{\Delta}^{2}\gg M^{2}_{S}\) в модели \((C)\), кажется наиболее оптимистичным сценарием для моделей, перечисленных в Таблице 1 (за исключением областей резонанса, которые также позволяют более лёгкие поля). В этом пределе тёмная материя может быть относительно лёгкой, \(M_{\text{\tiny DM}}\simeq 100\) ГэВ, и, следовательно, экзотические состояния \(\Delta\) и \(\mathcal{F}\) могут быть одновременно порядка нескольких сотен ГэВ. В принципе, возможно наблюдение всех трёх мультиплетов за пределами Стандартной Модели в этом пределе. Для других подходящих моделей в Таблице 1 тёмная материя должна быть относительно тяжелой: \(M_{\text{\tiny DM}}\gtrsim 500\) ГэВ для моделей инертного двойноготета и \(M_{\text{\tiny DM}}\gtrsim 2.5\) ТэВ для моделей инертного тройноготета. Это выходит за пределы области доступности дополнительных полей за пределами Стандартной Модели на ЛАК. Обратите внимание, что любая массовая вырожденность между заряженными и нейтральными членами инертного мультиплета на дереве устраняется радиационными эффектами, делая заряженные компоненты тяжелее нейтральных компонентов. Более тяжелые члены заданного мультиплета могут распадаться на более легкие члены того же мультиплета через слабые взаимодействия, например \(\mathcal{F}^{+}\to W^{+}+\mathcal{F}^{0}\), где \(W\) может быть виртуальным. Более тяжелый мультиплет также может распадаться на более легкий мультиплет через юкавское спаривание; например \(\mathcal{F}^{-}\to S^{0}+\ell^{-}\), если \(M_{\mathcal{F}}\gg M_{S}\). Из-за дискретной симметрии новые поля могут быть производимыми парами на коллайдерах, и сохранение заряда \(Z_{2}\) означает, что конечные состояния, возникающие из экзотических цепочек распада, обязательно включают стабильные электрически нейтральные поля, которые будут уклоняться от детектора. ## 6 Об истоке дискретной симметрии Возможно сделать следующее предположение, аналогичное предложению Ма: мы используем дискретную симметрию \(Z_{2}\), чтобы обеспечить стабильность наиболее легкого поля в диаграмме массы нейтрино вне Стандартной Модели. Можно возразить, что использование дискретной симметрии не полностью удовлетворяет, поскольку оно кажется добавочным, или из-за того, что расчеты квантовой гравитации не должны сохранять глобальные симметрии. Это мотивирует нас рассмотреть возможность найти простое объяснение для дискретной симметрии. Самая простая возможность - заменить дискретную симметрию на калиброванную симметрию \(U^{\prime}(1)\), которая не будет нарушаться квантовыми эффектами гравитации. С достаточным количеством дополнительных компонентов, вероятно, можно достичь этой цели для всех моделей, о которых мы говорили. Однако мы хотели бы знать, какие модели допускают минимальное расширение, такое что \(Z_{2}\) превращается в \(U^{\prime}(1)\), и в частицовом спектре добавляется только один скалярный синглет \(\eta\), чтобы нарушить симметрию \(U^{\prime}(1)\). Представляя полную калибровочную группу как \(\mathcal{G}_{\text{\tiny SM}}\times U(1)^{\prime}\), где \(\mathcal{G}_{\text{\tiny SM}}\) - это калибровочная группа стандартной модели, у нас имеются следующие свойства преобразования для полей за пределами Стандартной модели⁹ [FOOTNOTE:9][ENDFOOTNOTE] \[\eta\sim(1_{\text{\tiny SM}},Q_{\eta})\,,\quad S_{1,2}\sim(Q^{ \text{\tiny SM},}_{1,2},Q)\,,\quad\mathcal{F}\sim(Q^{\text{\tiny SM}}_{ \mathcal{F}},-Q),\] (34) \[\eta \sim (1_{\text{\tiny SM}}, Q_{\eta})\,,\quad S_{1,2} \sim (Q^{\text{\tiny SM}}_{1,2},Q)\,,\quad \mathcal{F} \sim (Q^{\text{\tiny SM}}_{\mathcal{F}}, -Q),\] (34) где верхний индекс "SM" обозначает заряды в рамках \(\mathcal{G}_{\text{\tiny SM}}\), приведенные в Таблице 1. Из анализа уравнения (3) видно, что все слагаемые Лагранжиана, необходимые для генерации массы нейтрино, допустимы симметрией \(U^{\prime}(1)\). Однако в случае моделей \((A)\) и \((B)\), являющихся моделями с инертным дуплетом, усиленная симметрия препятствует дополнительному слагаемому \((S_{1}^{\dagger}H)^{2}\). Это слагаемое необходимо для разделения нейтральных компонентов \(S_{1}\sim(1,2,1)\) и для избегания ограничений прямого обнаружения [10]. Таким образом, модели \((A)\) и \((B)\) несовместимы с этим минимальным расширением симметрии. С другой стороны, мы обнаружили, что модели \((C)\), \((D)\) и \((E)\), в которых один скаляр образует действительное представление симметрии калибровки СМ, остаются жизнеспособными моделями тёмной материи при условии \(Q_{\eta}=-2Q\). Это соотношение необходимо для снятия массовой вырожденности нейтральных полей за пределами СМ. Например, рассмотрим модель \((C)\), которая теперь имеет следующие члены в потенциале скаляра. \[V(H,S,\Delta,\eta) \supset \lambda_{\text{\tiny SH}}\left\{S\tilde{H}^{\dagger}\Delta^{ \dagger}H+S^{*}H^{\dagger}\Delta\tilde{H}\right\}\ +\ \frac{\mu_{\eta}}{2} \left\{S^{2}\eta+S^{*2}\eta^{\dagger}\right\},\] (35) в дополнение к терминам в уравнении (7). Все остальные термины, содержащие \(\eta\), зависят только от модуля \(|\eta|^{2}\). Мы использовали относительную фазу \(S\) и \(\Delta\) для выбора \(\lambda_{\text{\tiny SH}}\) вещественным и фазы \(S\) для выбора \(\mu_{\eta}\) вещественным. Обратите внимание, что нарушение симметрии \(U^{\prime}(1)\to Z_{2}\) достигается ненулевым значением \(\langle\eta\rangle\), что побуждает использовать дискретную симметрию как случайную подгруппу калибровочной симметрии \(U^{\prime}(1)\). В базисе \(\mathcal{S}=(S_{R},\Delta_{R},S_{I},\Delta_{I})^{T}\) матрица квадрата массы имеет следующий вид¹⁰ [FOOTNOTE:10][ENDFOOTNOTE] (SEE LAST LINE FOR TRANSLATION) \[\mathcal{M}^{2}=\left(\begin{array}[]{cccc}\hidden@noalign{}\hfil \tilde{M}_{S}^{2}+\lambda_{5}v^{2}+2\mu_{\eta}\langle\eta\rangle&\frac{\lambda _{\text{\tiny SH}}}{4}v^{2}&0&0\\ \hidden@noalign{}\hfil\frac{\lambda_{\text{\tiny SH}}}{4}v^{2}&\tilde{M}_{ \Delta}^{2}+\frac{\lambda_{4}}{2}v^{2}&0&0\\ \hidden@noalign{}\hfil 0&0&\tilde{M}_{S}^{2}+\lambda_{5}v^{2}-2\mu_{\eta} \langle\eta\rangle&\frac{\lambda_{\text{\tiny SH}}}{4}v^{2}\\ \hidden@noalign{}\hfil 0&0&\frac{\lambda_{\text{\tiny SH}}}{4}v^{2}&\tilde{M}_ {\Delta}^{2}+\frac{\lambda_{4}}{2}v^{2}\end{array}\right).\] (40) Обратите внимание, что записи для состояний с чётным и нечётным зарядами CP идентичны в пределе \(\mu_{\eta}\to 0\). Это приведёт к вырожденным состояниям, так что в случае, когда тёмная материя состоит в основном из \(\Delta\), тёмная материя будет исключена по данным эксперимента XENON100 (она будет инертной комплексной тройкой). Однако, при ненулевом \(\mu_{\eta}\) состояния с чётным и нечётным зарядами CP становятся не вырожденными, и достигается возможность существования тёмной материи. Когда тёмная материя состоит в основном (или полностью, для модели \((D)\)) из вещественного представления \(\mathcal{G}_{\text{\tiny SM}}\), разделение, достигаемое ненулевым \(\mu_{\eta}\), также обеспечивает подавление сигналов прямого обнаружения, возникающих из смешивания между \(Z^{\prime}\) и \(Z\).¹¹ [СНОСКА:11][КОНЕЦ СНОСКИ] Будет дополнительный рассеивающий процесс для темной материи из-за смешивания между \(\eta\) и скалярным полем СМ, что приводит к типичному взаимодействию через портал Хиггса. Учитывая, что связь для этого взаимодействия необходима для достижения наблюдаемой обили темной материи, всегда можно выбрать такое значение этой связи, чтобы оно было достаточно малым для соблюдения ограничений. Таким образом, с помощью этого простого расширения калибровки мы можем объяснить происхождение дискретной симметрии для моделей \((C)\), \((D)\) и \((E)\), сохраняя желательные свойства радиационной массы нейтрино и жизнеспособной обили темной материи. Обратите внимание, что исходное предложение Ма [3] и вариант, использующий реальный тройной фермион [4], не совместимы с этим минимальным улучшением симметрии; в случае скалярной темной материи термин \((S^{\dagger}H)^{2}\) исключен, что означает, что прямые эксперименты по обнаружению исключают модель, аналогично минимальному расширению моделей с калибровочным полем \((A)\) и \((B)\). Кроме того, возникают гауссовы аномалии, так как \(\mathcal{F}_{R}\) является хиральным полем в работах [3, 4] - для объяснения происхождения симметрии \(Z_{2}\) в этих случаях требуется дополнительное моделирование. Мы не затрагиваем этот вопрос здесь. ## 7 За пределами присоединенного представления В предыдущих разделах мы изучали обобщения модели Ма 2006 года с радиационной массой нейтрино и стабильными кандидатами на тёмную материю. При этом мы ограничились вниманием на мультиплеты размером не больше адъюнктного представления. Как уже упоминалось, можно получить массу нейтрино с помощью Рисунка 1 и получить кандидатов на тёмную материю в моделях с большими мультиплетами. Мы кратко обсудим этот вопрос в настоящем разделе. Сначала рассмотрим случай с включением массы Майораны, как показано на Рисунке 2. Разрешая представления \(SU(2)\) такие, как пятикратное представление, мы находим еще две модели. Оба из них используют четверкое скалярное поле \(S\sim(1,4,1)\), при этом реальное фермионное поле может быть либо трехкратным \(\mathcal{F}\sim(1,3,0)\), либо пятикратным \(\mathcal{F}\sim(1,5,0)\). Последняя модель была подробно рассмотрена в работе [38]. В обоих моделях возможно наличие как скалярной, так и фермионной темной материи, как и в первоначальном предложении Ма; нейтральное фермионное поле не связано с бозоном \(Z\) и, следовательно, может оставаться согласованным с ограничениями прямого обнаружения. [Сноска:12][КОНЕЦСНОСКИ] Обобщая модели с вставкой массы фермионов типа Дирака (т.е. обобщая модели в таблице 1), мы обнаруживаем, что возможны и другие варианты. Для полноты мы перечисляем их в приложении, но здесь мы предлагаем следующие комментарии. Как и в моделях в таблице 1, мы обнаруживаем, что для всех моделей с более крупными калибровочными представлениями фермионная темная материя может быть исключена. Фермионы остаются псевдо-дираковскими частицами с малыми разделениями, определенными массами нейтрино СМ. Такие малые разделения позволяют неограниченное рассеяние на уровне дерева с детекторами СМ через обмен бозоном \(Z\), что исключается экспериментом XENON100. Мы таким образом исключаем область параметров, в которой фермион является самым легким состоянием вне СМ, по тем же причинам, что и обсуждалось в разделе 3. В случае скалярной темной материи необходимо рассмотреть отдельные модели, как это требовалось для моделей в таблице 1. Некоторые модели могут быть сразу исключены по тем же причинам, по которым можно исключить модели \((F)\) и \((G)\); например, модель \((L)\) в таблице 2 может быть исключена, так как она дает невзаимодействующую комплексную модель тройтета. Аналогично, модель \((R)\) в таблице 3 исключается, так как \(S_{2}\) содержит только заряженные компоненты, а \(S_{1}\) имеет ненулевой гиперзаряд. Другие модели, кажется, совместимы с ограничениями прямого обнаружения, при условии смешивания нейтральных компонент скаляров, когда самый легкий скаляр имеет ненулевой гиперзаряд, подобно тому, как модели \((C)\) и \((E)\) являются жизнеспособными. Например, модель \((M)\) содержит \(S_{1}\sim(1,4,1)\) как единственный скаляр вне СМ с нейтральной компонентой. Однако в Лагранжиане существует член \(\lambda(S_{1}^{\dagger}H)^{2}\subset\mathcal{L}\), который может разделить компоненты нейтрального скаляра, позволяя избежать ограничений прямого обнаружения (это аналогично разделению, полученному в модели инертного двойноготта). Наконец, мы отмечаем, что использование более крупных мультиплетов может иметь дополнительное феноменологическое преимущество. Ссылаясь на работу [5], показывается, что большие мультиплеты, которые опосредуют взаимодействия между темной материей и Стандартной Моделью, могут усиливать процессы аннигиляции темной материи с помощью петель в \(2\gamma\) и \(\gamma+Z\) конечные состояния, без необходимости в непертурбативно больших связях. Это происходит потому, что большие мультиплеты позволяют полям иметь большие электрические заряды, естественно усиливая процессы с петлями и фотонами в конечном состоянии. Кажется, что в моделях, представленных в Приложении, невозможно реализовать астрофизический сигнал гамма-лучей [6], но простые расширения кажутся совместимыми с этой идеей. Например, модель \((N)\) в Таблице 3 использует \(\mathcal{F}\sim(1,4,-1)\), \(S_{1}\sim(1,5,0)\) и \(S_{2}\sim(1,5,2)\). Когда \(S_{1}\) является самым легким за пределами Стандартной Модели состоянием, темная материя состоит (в основном) из нейтральной компоненты \(S_{1}\). В однопетлевом вкладе в процессы типа \(DM+DM\to 2\gamma,\gamma+Z\) имеются виртуальные состояния \(S_{2}\) в петле, которые усиливаются за счет наличия многократно заряженной компоненты в \(S_{2}\). Заметим, что масса темной материи должна быть либо \(M_{\text{\tiny DM}}\sim 130\) ГэВ, либо \(M_{\text{\tiny DM}}\sim 144\) ГэВ, чтобы генерировать избыток гамма-лучей через аннигиляции темной материи в \(2\gamma\) или \(\gamma+Z\) конечные состояния соответственно. Однако, ожидается, что темная материя, состоящая из \(S_{1}\sim(1,5,0)\), должна иметь массу \(M_{\text{\tiny DM}}\gtrsim 5\) ТэВ, чтобы достичь правильной избыточности [11], что слишком велико для объяснения астрофизического сигнала. Если добавить синглетный скаляр \(S\), который также является нечетным относительно симметрии \(Z_{2}\), в модель, то область параметров, где \(S\) является темной материей, совместима с \(M_{\text{\tiny DM}}\sim 130\) ГэВ или \(M_{\text{\tiny DM}}\sim 144\) ГэВ. Компоненты \(S_{1}\) и/или \(S_{2}\) могут быть \(\mathcal{O}(100)\) ГэВ, и петлевые процессы, поддерживаемые в работе [5], присутствуют в модели, таким образом усиливая астрофизический сигнал гамма-лучей. В этом примере имеется простая связь между астрофизическим сигналом и механизмом массы нейтрино, крупные мультиплеты, которые обеспечивают последнюю, также усиливают первую. Было бы интересно продолжить развивать эти идеи, чтобы увидеть, может ли темная материя быть реализована одним из полей в диаграмме петель нейтрино, а не дополнительной степенью свободы, или исследовать феноменологию только что описанной модели. [FOOTNOTE:13][ENDFOOTNOTE] Отобразить примечание и конец примечания в исходном виде. ## 8 Заключение Мы изучали класс моделей с радиационной массой нейтрино и стабильными кандидатами на темную материю. Масса нейтрино была получена с помощью диаграммы однократного рассеяния с той же топологией, что и предложил Ма [3]. Мы обобщили подход Ма, детализируя все варианты с полем выше Стандартной Модели, не превышающим адъюнктное представление. В случае, когда в диаграмме массы нейтрино присутствовало массовое включение Майораны, было найдено только две модели, обе из которых были известны. Когда включение массы было типа Дирака, так что симметрия числа лептонов была нарушена вершиной, было найдено несколько дополнительных моделей. Фермионная темная материя была исключена во всех этих моделях, в то время как две из них были полностью исключены из-за ограничений прямого обнаружения. Оставшиеся модели позволяли радиационную массу нейтрино и достигали жизнеспособного избытка (скалярной) темной материи. Были случаи с инертным синглетом, инертным двойником и инертным тройником, обеспечивающие естественную среду для моделей инертных темной материи N-кортежей с дополнительной возможностью достижения радиационной массы нейтрино. Интересно, что некоторые из моделей позволяли простое расширение, при котором (ранее наложенная) дискретная симметрия возникала как случайная симметрия на низких энергиях. Мы кратко обсудили модели с более крупными полевыми кратностями выше Стандартной Модели, показывая, что существуют жизнеспособные сценарии. С помощью простых расширений большие кратности, позволяющие массу нейтрино, также могут усиливать сигналы гамма-излучения астрофизических источников в настоящее время, позволяя простую связь между механизмом массы нейтрино и сигналом астрофизического гамма-излучения. ## Подтверждения Авторы благодарят Y. Kajiyama, K. Nagao, H. Okada, T. Schwetz, A. Strumia и K. Yagyu. SSCL частично поддерживается NSC в рамках гранта № NSC-101-2811-M-006-015 и частично - NCTS Тайваня. KM поддерживается Австралийским советом по научным исследованиям. ## Приложение А Масса без симметрии \(\mathbf{Z_{2}}\) Из моделей, представленных в Таблице 1, только модели \((A)\), \((B)\) и \((D)\) ожидаются создать (доминирующие) радиационные массы нейтрино в отсутствие симметрии \(Z_{2}\). Другие модели содержат тройной скаляр \(S_{1,2}\sim(1,3,2)\), который акоплирует по Юкаве с лептонами СМ и приобретает ВЭО за счет термина \(\mu HS_{1,2}H\subset V(H,S_{1},S_{2})\) в отсутствие дискретной симметрии. Таким образом, ожидается, что массы нейтрино на уровне дерева стандартной формы смешивания типа II [40] будут превалировать над эффектом петли, когда симметрия \(Z_{2}\) отклоняется. В случае моделей \((A)\), \((B)\) и \((D)\), с другой стороны, массы нейтрино на уровне дерева не возникают, если симметрия \(Z_{2}\) устранена, тогда как диаграмма петли на Рисунке 1 сохраняется. Обратите внимание, что если симметрия \(Z_{2}\) отключена, фермион \(\mathcal{F}\) не требуется для создания ненулевых радиационных масс нейтрино в модели \((D)\)[41]. Однако спектр, полученный без \(\mathcal{F}\), имеет простую форму Zee [41], которая несовместима с наблюдаемой смешивающей структурой [42]. Таким образом, фермион \(\mathcal{F}\sim(1,2,-1)\) необходим для получения "жизнеспособной" смешивающей структуры в отсутствие симметрии \(Z_{2}\). [ССЫЛКА В СНОСКУ:14][КОНЕЦ ССЫЛКИ] Модель \((B)\) имеет схожий состав частиц с моделью, представленной в ссылке [43], за исключением замены \(S_{2}\sim(1,2,3)\to S_{2}\sim(1,4,3)\). Это различие исключает древесную массу, найденную в ссылке [43], поэтому модель \((B)\) является чисто моделью радиационных масс, которую можно изучать без дискретной симметрии и тёмной материи.¹⁵ [FOOTNOTE:15][ENDFOOTNOTE] (ru) ## Приложение Б Модели с более крупными мультиплетами В тексте мы нашли семь моделей, которые используют мультиплеты за пределами СМ либо в фундаментальном, либо в присоединенном представлении \(SU(2)_{L}\) и имеют внутреннюю вставку массы Дирака. Помимо этих минимальных моделей, можно реализовать радиационную массу нейтрино и кандидатов в темную материю с использованием больших мультиплетов. Мы представляем дополнительные минимальные модели, возникающие, если разрешить использование мультиплетов, формирующих квадруплетное ( изоспин \(3/2\)) представление \(SU(2)_{L}\) в Таблице 2. Схема маркировки следует из Таблицы 1 в тексте. Если разрешить использование мультиплетов, состоящих из пяти частиц, возникают дополнительные модели, показанные в Таблице 3 (см. также Ссылку [44] для детального примера). Первый случай, указанный как модель \((M)\), был представлен в Ссылке [15]. [TABLE:A2.T2][ENDTABLE] [TABLE:A2.T3][ENDTABLE] ## Ссылки * [1] M. C. Гонсалес-Гарсия, M. Малтони, J. Сальвадо и T. Швец, JHEP **1212**, 123 (2012) [arXiv:1209.3023 [hep-ph]]. * [2] A. H. G. Peter, arXiv:1201.3942 [astro-ph.CO]. * [3] E. Ma, Phys. Rev. D **73**, 077301 (2006) [hep-ph/0601225]. * [4] E. Ma и D. Suematsu, Mod. Phys. Lett. A **24**, 583 (2009) [arXiv:0809.0942 [hep-ph]]. * [5] J. Kopp, E. T. Neil, R. Primulando и J. Zupan, Phys. Dark. Univ. **2** (2013) 22 [arXiv:1301.1683 [hep-ph]]. * [6] C. Weniger, JCAP **1208**, 007 (2012) [arXiv:1204.2797 [hep-ph]]. * [7] L. M. Краусс, S. Nasri и M. Тродден, Phys. Rev. D **67**, 085002 (2003) [hep-ph/0210389]. * [8] C. Boehm, Y. Фарзан, T. Hambye, S. Palomares-Ruiz и S. Pascoli, Phys. Rev. D **77**, 043516 (2008) [hep-ph/0612228]; M. Lindner, D. Schmidt и T. Швец, Phys. Lett. B **705**, 324 (2011) [arXiv:1105.4626 [hep-ph]]; F. -X. Josse-Michaux и E. Molinaro, Phys. Rev. D **84**, 125021 (2011) [arXiv:1108.0482 [hep-ph]]; S. Канемура, Т. Набэсима и Х. Сугияма, Phys. Rev. D **85**, 033004 (2012) [arXiv:1111.0599 [hep-ph]]; M. Gustafsson, J. M. Но и M. A. Rivera, arXiv:1212.4806 [hep-ph]; M. Аоки, J. Кубо и H. Такано, arXiv:1302.3936 [hep-ph]; Y. Каджияма, H. Окада и Т. Тома, arXiv:1303.7356 [hep-ph]. * [9] V. Сильвейра и A. Зи, Phys. Lett. B **161**, Переведите маркдаун с английского на русский. Сохраните формулы:

# On the nature of Seyfert galaxies with high [OIII]5007 blueshifts S. Komossa Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany; [email protected] D. Xu National Astronomical Observatories, Chinese Academy of Science, A20 Datun Road, Chaoyang District, Beijing 100012, China H. Zhou Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany T. Storchi-Bergmann Instituto de Fisica, UFRGS, Campus do Vale, CP 15051, Porto Alegre 91501-970, RS, Brazil L. Binette Département de Physique, de Génie Physique et d’Optique, Université Laval, Québec, QC, G1K7P4, Canada; and Instituto de Astronomia, UNAM, Ap. 70-264, 04510 México, DF, México ###### Abstract We have studied the properties of Seyfert galaxies with high [OIII]5007 blueshifts (“blue outliers”), originally identified because of their strong deviation from the \(M_{\rm BH}-\sigma\) relation of normal, narrow-line Seyfert 1 (NLS1) and broad-line Seyfert 1 (BLS1) galaxies. These blue outliers turn out to be important test-beds for models of the narrow-line region (NLR), for mechanisms of driving large-scale outflows, for links between NLS1 galaxies and radio galaxies, and for orientation-dependent NLS1 models. We report the detection of a strong correlation of line blueshift with ionization potential in each galaxy, including the measurement of coronal lines with radial velocities up to 500–1000 km s\({}^{-1}\), and we confirm a strong correlation between [OIII] blueshift and line width. All [OIII] blue outliers have narrow widths of their broad Balmer lines and high Eddington ratios. While the presence of non-shifted low-ionization lines signifies the presence of a classical outer quiescent NLR in blue outliers, we also report the absence of any second, non-blueshifted [OIII] component from a classical inner NLR. These results place tight constraints on NLR models. We favor a scenario in which the NLR clouds are entrained in a decelerating wind which explains the strong stratification and the absence of a zero-blueshift inner NLR of blue outliers. The origin of the wind remains speculative at this time (collimated radio plasma, thermal winds, radiatively accelerated clouds). It is perhaps linked to the high Eddington ratios of blue outliers. Similar, less powerful winds could be present in all Seyfert galaxies, but would generally only affect the coronal line region (CLR), or level off even before reaching the CLR. Similarities between blue outliers in NLS1 galaxies and (compact) radio sources are briefly discussed. Subject headings: galaxies: active – galaxies: evolution – galaxies: individual (SBS0919+515, SDSSJ115533.50+010730.4, RXJ01354-0043, NGC450#86, SDSSJ032606.75+011429.9, IRAS11598-0112, SDSSJ171828.99+573422.3, PG1244+026, RXJ09132+3658) – galaxies: Seyfert – quasars: emission lines ## 1. Introduction The concept of feedback due to outflows is a potential key ingredient in understanding the coevolution of galaxies and black holes (Silk & Rees 1998, Fabian 1999, Wyithe & Loeb 2003). Recent analytic estimates and simulations demonstrate the importance of feedback from winds/outflows for instance in cosmic downsizing (Scannapieco et al. 2005), in fixing the \(M_{\rm BH}-\sigma\) relation (di Matteo et al. 2005), and in determining galaxy colors (Springel et al. 2005) by regulating star formation in the host galaxy. Powerful gaseous outflows in Active Galactic Nuclei (AGN) deposit mass, energy and metals in the interstellar medium of the galaxy and the intergalactic medium or intracluster medium (Colbert et al. 1996, Churazov et al. 2001, Moll et al. 2007). AGN winds also play a potentially important role in unified models of AGN (Elvis 2000, 2006). Observational evidence for outflows in AGN exists on various scales and in all wavebands from the radio (Morganti et al. 2005, Gallimore et al. 2006), to the IR (Rodriguez-Ardila et al. 2006), optical (Das et al. 2005), UV (Sulentic et al. 2007, Rodriguez Hidalgo et al. 2007, Crenshaw & Kraemer 2007), and X-ray band (Chelouche & Netzer 2005, Krongold et al. 2007); see Veilleux et al. (2005) for a review. There are several lines of evidence that outflows are particularly strong in narrow-line Seyfert 1 (NLS1) galaxies. NLS1 galaxies are a subclass of AGN with extreme emission-line and continuum properties which appear to be in part driven by their high Eddington ratios, low black hole masses, and other parameters (e.g., Osterbrock & Pogge 1985, Boroson 2002, Grupe 2004; see Komossa 2008 for a review). The high Eddington ratios likely lead to strong, radiation-pressure driven outflows. As a class of objects with low black hole masses, high accretion rates and strong winds, the location of NLS1 galaxies on the \(M_{\rm BH}-\sigma\) plane is of special interest (Mathur et al. 2001; see our Sect. 4.1). Komossa & Xu (2007) have shown that NLS1 galaxies follow the same \(M_{\rm BH}-\sigma\) relation as normal and broad-line Seyfert 1 (BLS1) galaxies, if the width of the [SII]6716,6731 emission lines is used as a surrogate for stellar velocity dispersion. The width of [OIII]5007 (after removal of asymmetric blue wings) is still a good proxy for stellar velocity dispersion in BLS1 and NLS1 galaxies, with one important exception. A subset of NLS1 galaxies deviates systematically from the \(M_{\rm BH}-\sigma\) relation, and all of these are characterized by high [OIII] _blueshifts_. At the same time, the [SII]-based measurements of velocity dispersion of the same objects still place them _on_ the \(M_{\rm BH}-\sigma\) relation (Fig. 1). Therefore, the [OIII] lines of these particular galaxies were not suitable to estimate \(\sigma\). However, the independent question is raised as to which mechanism drives these [OIII] line blueshifts, and what we can learn from them regarding the nature of these systems and perhaps the evolutionary state of NLS1 galaxies. That is the topic of this study. A measurable difference in blueshifts and widths of different NLR emission lines has been recognized early (review by Osterbrock 1991). The phenomenon of strong [OIII] blueshifts exceeding one–several hundred km s\({}^{-1}\) (so-called blue outliers), is more rare. It has been detected early in individual objects (Phillips 1976) but has only been studied systematically recently (Zamanov et al. 2002, Marziani et al. 2003, Aoki et al. 2005, Boroson 2005, Bian et al. 2005). These studies have shown that blue outliers have high Eddington ratios and small Balmer line widths (all of them with FWHM(H\(\beta\)) \(<\) 4000 km s\({}^{-1}\), and most of them with FWHM(H\(\beta\)) \(<\) 2000 km s\({}^{-1}\); Marziani et al. 2003). It has remained uncertain whether there is (Bian et al. 2005) or is not (Aoki et al. 2005) a direct correlation between [OIII] blueshift and Eddington ratio. Common to most studies is the presence of a strong correlation between [OIII] blueshift and [OIII] line width. This correlation is also known among iron coronal lines of BLS1 galaxies (Penston et al. 1984, Erkens et al. 1997). The reason is not yet well understood. Outflows are thought to play a role in explaining the phenomenon. Except Boroson (2005) all sample studies concentrated on the [OIII]-H\(\beta\) region of optical spectra of blue outliers in order to examine the phenomenon, while for the first time we include information from all the detected optical NLR lines. We report the detection of strong correlations and discuss consequences for the nature of blue outliers and for dynamical NLR models. This paper is organized as follows. In Sect. 2 we describe the sample selection and provide details on the data analysis. Results on trends and correlations are presented in Sect. 3 which are then discussed in Sect. 4. A summary and conclusions are given in Sect. 5. Some individual objects turn out to be remarkable. Notes on them are provided in an Appendix. We use a cosmology with \(H_{\rm 0}\)=70 km s\({}^{-1}\) Mpc\({}^{-1}\), \(\Omega_{\rm M}\)=0.3 and \(\Omega_{\rm\Lambda}\)=0.7 throughout this paper. ## 2. Data analysis ### The sample The nine NLS1 galaxies of the present work were drawn from the sample of Xu et al. (2007, 2008). The original sample selection and standard data reduction procedures were described in detail in that work. In brief, the sample consists of NLS1 galaxies from the catalogue of Véron-Cetty & Véron (2003) and a comparison sample of BLS1 galaxies from Boroson (2003) at redshift \(z<0.3\), which have Sloan Digital Sky Survey (SDSS) DR3 (Abazajian et al. 2005) spectra available and which have detectable low-ionization lines (presence of [SII]6716,6731, with S/N\(>\)5). The BLS1 and NLS1 galaxy samples have similar redshift and absolute magnitude distributions. Xu et al. (2007) corrected the SDSS spectra for Galactic extinction, decomposed the continuum into host galaxy and AGN components, and then subtracted the host galaxy contribution and the FeII complexes from the spectra. Emission line profiles of the galaxies were fit with Gaussians using the IRAF package SPECFIT (Kriss 1994). Measured FWHMs were corrected for instrumental broadening. Re-classification after spectral emission-line fitting led to 39 BLS1 and 55 NLS1 galaxies in the sample. We focus here on the nine galaxies with the highest blueshifts of [OIII] (Tab. 1) which were identified by Komossa & Xu (2007; KX07 hereafter). Results from the complete NLS1 (and BLS1) sample are shown for comparison purposes, and in order to identify trends across the whole BLS1 – NLS1 – blue-outlier population. When we report measurements of optical FeII strength (FeII4570), this is the integrated flux of the FeII emission complex between the rest wavelengths 4434Å and 4684Å. We refer to the flux sum of the two Sulphur lines, [SII]6716 and [SII]6731, as [SII]6725. ### Emission-line fits and [OIII] profile The Balmer lines were decomposed into three components, narrow core (H\(\beta_{\rm n}\); FWHM fixed to that determined for [SII]6716,6731), and two broad components. No physical meaning is ascribed to the two separate broad components; they merely serve as a mathematical description (see Xu et al. 2008 for alternative Lorentzian fits). The final width of the broad-line emission, H\(\beta_{\rm b}\), is determined as the FWHM of the sum of the two Gaussians. With the exception of [OIII], forbidden lines are well represented by single Gauss profiles. The total [OIII] emission-line profile, [OIII]\({}_{\rm totl}\), was decomposed into two Gaussian components, a narrow core ([OIII]\({}_{\rm c}\)) and broad base. We distinguish between two types of [OIII] spectral complexity: (1) the presence of such a broad base which tends to be blue-asymmetric (e.g., Heckman et al. 1981), and is referred to as “blue wing”, and (2) systematic blueshifts of the whole core of [OIII]. Objects which show this latter phenomenon are called “blue outliers” (Zamanov et al. 2002)¹. Measurements of the FWHM and blueshift of [OIII] reported in this work refer to the core of the emission-line, unless noted otherwise. [FOOTNOTE:1][ENDFOOTNOTE] Ideally, measurements of the velocity shift of [OIII] should be done relative to the galaxy restframe, as defined by stellar absorption lines from the host galaxy. However, these features are generally weak or absent in our galaxies (and in NLS1 galaxies in general). We therefore measure velocity shifts of [OIII] and of all other lines relative to [SII]. We use positive velocity values to refer to blueshifts, negative ones for redshift. The shifts of H\(\beta\) and other low-ionization lines ([OI]6300, NII[6584], [OII]3727) agree well with [SII], while other high-ionization lines ([NeIII]3861, [NeV]3426, and iron coronal lines) are characterized by high blueshifts (Sect. 3.3). If lines were too faint to be fit by a Gaussian of free width, we used fixed width instead (fixed to FWHM([SII]) for low-ionization lines or to FWHM([OIII]\({}_{\rm c}\)) for high-ionization lines) and determined the central wavelength to measure the blueshift. Results are reported in Tab. 1. Since the redshifts provided by the SDSS pipeline are determined based on all strong detected emission lines and are therefore influenced by the blueshifted [OIII], we have re-measured redshifts based on H\(\beta_{\rm n}\). It is these redshifts that are given in Tab. 1. We have measured the average [OIII]\({}_{\rm totl}\)/[SII]6725 ratios of our BLS1 and NLS1 galaxy sample. We find that, in terms of this ratio, their NLRs are similar, with \(<\)[OIII]\({}_{\rm totl}\)/[SII]6725\(>\)=5 in BLS1 galaxies, and \(<\)[OIII]\({}_{\rm totl}\)/[SII]6725\(>\)=4 in NLS1 galaxies. Notes on individual objects are given in the Appendix. Here, we briefly comment on the detection of [FeX]6375 in two blue outliers. In PG1244+026 [FeX] is blended with [OI]6365. For decomposition, the width of [OI]6365 was fixed to that of [OI]6300. The two-component fit then reproduces the expected ratio of [OI]6300/[OI]6365 \(\approx\) 3. [FeX] is blueshifted by 640 km s\({}^{-1}\). In RXJ0135\(-\)0043, [FeX] overlaps with atmospheric O\({}_{2}\) which is imperfectly corrected for. Therefore, the width of [FeX] was fixed to that of [OIII]. This gives an outflow velocity of 990 km s\({}^{-1}\). ### Robustness of spectral fits: continuum and line decomposition In order to see how much the fitting procedure affects measurements of [OIII] fluxes, asymmetries and blueshifts, we have repeated the spectral analysis several times under different conditions and assumptions: We have fit the host-galaxy-corrected, FeII subtracted spectrum and for comparison the original SDSS spectrum without any of these corrections. We have re-fit the [OIII] profile in a number of different ways, and with different Gaussian decompositions. The [OIII] profile was fit using the red half of the profile only, or different fractions of the total profile, or only the upper 30% of the profile, or with a single and a double Gaussian profile. Fitting the profile with one single Gaussian component maximizes the blueshift in objects with significant [OIII] blue wings. In all other cases, uncertainties in line blueshifts due to non-subtraction of a host galaxy contribution and due to different line fitting procedures are typically much less than 50 km s\({}^{-1}\). The blueshift independently determined from the weaker line [OIII]4959 also agrees with [OIII]5007 within better than 50 km s\({}^{-1}\). Four of our galaxies are also in the sample of Boroson (2005). His [OIII] blueshift measurements agree with ours within typically better than \(\pm\)10 km s\({}^{-1}\). Uncertainties in FWHM of the core of [OIII] are typically 30% for [OIII] lines with extra blue wing (smaller in others), and are due to uncertainties in decomposition. We note in passing that the frequency of [OIII] blue wings in blue outliers is neither particularly high nor low (see also Boroson 2005). ## 3. Results ### Constraints on the presence/absence of blueshifted emission lines In order to facilitate a systematic discussion of NLR models of blue outliers (Sect. 4.3), we have investigated whether the non-shifted low-ionization lines have a (faint) high-ionization [OIII] counterpart and vice versa². We did this representatively for the three galaxies with the highest [OIII] blueshifts (SBS0919+515, SDSSJ11555+0107 and RXJ01354\(-\)0043), and for the galaxy with the highest S/N (PG1244+026). We have examined the following three questions: [FOOTNOTE:2][ENDFOOTNOTE] (1) Is there any [OIII] emission at zero blueshift present in the spectrum (which could originate from the inner NLR; or be counterpart to the low-ionization emission lines from the outer NLR) ? In order to test this, we have enforced an extra Gaussian line contribution to [OIII] at zero blueshift (or at \(v_{\rm[OIII]}=50\) km s\({}^{-1}\), the average value of our NLS1 sample excluding blue outliers) and of fixed FWHM([OIII]\({}_{\rm extra}\))=FWHM([SII]). We find that, if present, it must be very weak. The average ratio [OIII]\({}_{\rm totl}\)/[SII]6725 in our BLS1 sample is 5, while in our NLS1 sample it is 4. This value of 4 is much higher than the upper limit on the extra component which was fit to the observed spectra: Typically, [OIII]\({}_{\rm extra}\)/[SII]6725 \(\approx 0.1-0.4\), and always, [OIII]\({}_{\rm extra}\)/[SII]6725 \(<1\). Since the ratio of [OIII]/[SII] of nearby Seyfert galaxies generally decreases in dependence of radius (in models and observations; Komossa & Schulz 1997, Bennert et al. 2006) and since there must be an [OIII] contribution from the outer [SII] emitting clouds, the limits derived on any non-blueshifted [OIII] contribution from the _inner_ NLR are very tight. (2) Does the blueshifted [OIII] have a blueshifted H\(\beta\) counterpart ? I.e., how much highly blueshifted H\(\beta\) could be ‘hidden’ in the H\(\beta\) profile ? In order to check this, we have re-fit H\(\beta\) adding an additional Gaussian to describe its profile with parameters of this extra component fixed at \(v_{\rm H\beta_{extra}}=v_{\rm[OIII]_{c}}\), FWHM(H\(\beta_{\rm extra}\))=FWHM([OIII]\({}_{\rm c}\)) and an intensity ratio [OIII]\({}_{\rm c}\)/H\(\beta_{\rm extra}\)=10. We find that such a weak component could generally be hidden in the H\(\beta\) profile. (3) Does the blueshifted [OIII] have a blueshifted low-ionization counterpart in [SII] ? This is not the case. For typical _spatially averaged_ ratios of [OIII]/[SII]6725 \(\approx\)4 of our NLS1 sample, blueshifted [SII] lines would have generally been detectable, but are absent. Very faint blueshifted [SII], as it may arise in the _inner_ NLR, cannot be excluded with the present data. In summary, we find (1) little evidence for zero-blueshift [OIII] emission (the amount of emission consistent with the spectra likely originates from the outer parts of the NLR which also emits in [SII] and other low-ionization lines); (2) an extra blueshifted component in H\(\beta\) – the expected counterpart to blueshifted [OIII]– can be hidden in the H\(\beta\) profile; and (3) there is no detectable highly blueshifted component in the low-ionization lines. ### Estimates of black holes masses, Eddington ratios and NLR densities Black hole masses were estimated by using the radius(\(R_{\rm BLR}\))-luminosity(\(L\)) relation of BLS1 galaxies as reported by Kaspi et al. (2005) and the width of H\(\beta\). The luminosities at 5100Å were taken from Xu et al. (2008) and are based on SDSS g* and r* magnitudes corrected for Galactic extinction. Since we lack multi-wavelength spectral energy distributions, the bolometric luminosity \(L_{\rm bol}\) was estimated using a standard bolometric correction of \(L_{\rm bol}=9\,\lambda{L_{\rm 5100}}\) (Kaspi et al. 2000). \(L_{\rm Edd}\) was calculated from the black hole mass, according to \(L_{\rm Edd}=1.3\,10^{38}\) M\({}_{\rm BH}\)/M\({}_{\odot}\) erg/s. Typical errors in individual BH mass estimates can be as large as 0.5 dex, and arise from the use of single-epoch data, and uncertainties in H\(\beta\) decomposition and in host galaxy contribution. The NLR density was derived from the density-sensitive [SII] intensity ratio, [SII]6716/[SII]6731 (Xu et al. 2007). ### Trends and correlations We have checked for (1) trends of outflow velocity with other (atomic) parameters within each single spectrum, and (2) for trends across our sample of blue outliers (do all blue outliers have high Eddington ratios, high black hole masses, etc. ?), and (3) for trends across our whole sample of BLS1 and NLS1 galaxies. #### 3.3.1 A strong correlation of line shift with ionization potential We detect a strong correlation between emission-line blueshift and ionization potential (Fig. 3). While the low-ionization forbidden lines of [OI], [OII] and [NII], and the Balmer lines H\(\alpha\) and H\(\beta\) are at velocities very similar to [SII], high-ionization lines on the other hand show strong blueshifts which increase with ionization potential. Two galaxies (SDSSJ115533.50+010730.4 and PG1244+026) show extreme blueshifts in [Fe X], on the order of 600-1000 km s\({}^{-1}\). There is also a correlation between outflow velocity and critical density of the individual line transitions (Fig. 3), but it is less tight in the sense that [OI]6300, which has low ionization potential but high critical density, does not follow the trend. #### 3.3.2 Trends and correlations of [OIII] blueshift with line and galaxy parameters We have correlated the [OIII] blueshifts (of the blue outliers, and of our sample as a whole) with various other line parameters (line widths, line ratios) and with galaxy properties (absolute magnitude, black hole mass, Eddington ratio, NLR density). The strongest correlation is the one between [OIII] blueshift and [OIII] line width (Spearman rank correlation coefficient \(r_{\rm S}\)=0.6 for the whole NLS1 sample and even higher for just the blue outliers; Fig. 3). Within the NLS1 sample, there is a trend that blue outliers preferentially avoid low Eddington ratios \(L/L_{\rm edd}\) and low FeII/H\(\beta\) ratios. Most blue outliers have small ratios of [OIII]/H\(\beta_{\rm totl}\). We do not find trends of outflow velocity with NLR density \(n_{\rm e}\), black hole mass, absolute magnitude \(M_{\rm i}\), and the width of the broad component of H\(\beta\) (Fig. 4). However, while trends are absent within the NLS1 population itself, it is interesting to note that the presence of blue outliers amplifies trends which become apparent when the BLS1 galaxies are added to the correlation plots (Fig. 4). ### Frequency of blue outliers Among our sample, blue outliers only occur in NLS1 galaxies. At a velocity \(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}150\) km s\({}^{-1}\), we have a blue outlier fraction of 16%. If we use \(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}250\) km s\({}^{-1}\) instead, as in Zamanov et al. (2002), the fraction of blue outliers among NLS1 galaxies is 5%. ## 4. Discussion ### The locus of Seyfert galaxies with [OIII] blueshifts on the \(M_{\rm BH}-\sigma\) plane Investigating the location of different types of galaxies on the \(M_{\rm BH}-\sigma\) plane, and their potential evolution across the plane, is of great interest in the context of galaxy formation and evolution models. In AGN, stellar velocity dispersion is often difficult to measure, and the width of [OIII] has become a convenient proxy for stellar velocity dispersion (e.g., Terlevich et al. 1990, Whittle 1992, Nelson & Whittle 1996, Nelson 2000, Shields et al. 2003, Boroson 2003, Greene & Ho 2005, Netzer and Trakhtenbrot 2007, Salviander et al. 2007) after removing [OIII] blue wings and excluding galaxies with powerful kiloparsec-scale linear radio sources. The scatter in the relation is larger than in the original \(M_{\rm BH}-\sigma_{*}\) relation (Ferrarese & Merritt 2000, Gebhardt et al. 2000), and indicates secondary influences on the gas kinematics (e.g., Nelson & Whittle 1996, Rice et al. 2006). Mathur et al. (2001) pointed out the importance of studying the locus of NLS1 galaxies on the \(M_{\rm BH}-\sigma\) plane, which was the focus of a number of subsequent studies (Wang & Lu 2001, Wandel 2002, Botte et al. 2004, 2005, Bian et al. 2004, Grupe & Mathur 2004, Barth et al. 2005, Greene & Ho 2005, Mathur & Grupe 2005a,b, Zhou et al. 2006, Ryan et al. 2007, Watson et al. 2007, Komossa & Xu 2007). Any such study would involve one important step: the distinction between true outliers from the \(M_{\rm BH}-\sigma\) relation on the one hand, and apparent outliers on the other hand. Apparent outliers would only appear to be off-set from the \(M_{\rm BH}-\sigma\) relation because either the choice of line width as a measure of stellar velocity dispersion was unsuitable, or the choice of line and continuum parameters as a measure of black hole mass was unsuitable. KX07 have shown that those NLS1 galaxies of their sample which deviate significantly from the \(M_{\rm BH}-\sigma\) relation of normal (and BLS1) galaxies are all characterized by high [OIII] blueshifts. While these [OIII] lines were therefore not suited as surrogate for stellar velocity dispersion, the [SII]-based measurements of velocity dispersion of the very same objects still located them on the \(M_{\rm BH}-\sigma\) relation. Almost all galaxies which deviate most strongly from the \(M_{\rm BH}-\sigma\) relation (see our Fig. 1) show \(v_{\rm[OIII]}>150\) km s\({}^{-1}\). These six objects, plus three additional ones which also show \(v_{\rm[OIII]}>150\) km s\({}^{-1}\) define the nine blue outliers that are the target of the present study. In order to measure systematically the deviation of a galaxy from the \(M_{\rm BH}-\sigma_{*}\) relation, we define the quantity \(\Delta\sigma:=\log\sigma_{obs}-\log\sigma_{pred}\) (as in KX07), where \(\sigma_{obs}\) is the observed emission-line velocity dispersion, and \(\sigma_{pred}\) is the stellar velocity dispersion predicted from the \(M_{\rm BH}-\sigma_{*}\) relation of Ferrarese & Ford (2005). We find a strong correlation between [OIII] blueshift \(v_{\rm[OIII]}\) and \(\Delta\sigma\) (Fig. 1). This finding demonstrates that [OIII] velocity shift systematically affects the deviation of an object from the \(M_{\rm BH}-\sigma\) relation (see also Boroson 2005). We further find that a correlation between \(L/L_{\rm Edd}\) and \(\Delta\sigma\) (e.g., Mathur & Grupe 2005, Greene & Ho 2005; see also Netzer & Trakhtenbrot 2007) is only present in our sample if we include blue outliers; when they are removed from the sample, no correlation remains (last panel of our Fig. 4, see also KX07). Two of our NLS1 blue outliers have independent BH mass estimates. From X-ray variability, Czerny et al. (2001) estimated \(\log M_{\rm{BH}}=5.9\) for PG1244+062 which agrees well with our estimate from applying the \(R_{\rm BLR}\)-\(L\) relation (\(\log M_{\rm{BH}}=6.2\)). For RX01354\(-\)0043 we directly measured \(\sigma_{*}\) from stellar absorption lines (see Appendix). The value agrees well with \(\sigma_{\rm[SII]}\) and puts RXJ01354\(-\)0043 almost perfectly on the \(M_{\rm{BH}}\)-\(\sigma_{*}\) relation (Fig. 1). These findings demonstrate the importance of measuring [OIII] blueshifts, and removing objects with high blueshifts from a sample before putting it on the \(M_{\rm BH}-\sigma_{\rm[OIII]}\) relation. The independent question arises as to what may cause the blueshifts of these [OIII] outliers. ### Blue outliers: trends and correlations The phenomenon of slightly different blueshifts and line widths of NLR emission lines has been recognized since the early days of AGN spectroscopy and is generally traced back to a certain stratification of the NLR in the sense that high-ionization lines are produced preferentially at small distances from the core, while low-ionization lines are preferentially produced at larger radii (e.g., Osterbrock 1991). The presence of a strong [OIII] blueshift on the order of several hundred km s\({}^{-1}\) was noticed early in the prototype NLS1 galaxy IZw1³ (e.g., Phillips 1976, Véron-Cetty et al. 2004). The galaxy also shows very blueshifted IR coronal lines (Schinnerer et al. 1998) and blueshifted UV high-ionization broad lines (Laor et al. 1997). [FOOTNOTE:3][ENDFOOTNOTE] Several recent studies systematically examined the phenomenon of blue outliers in larger samples of type 1 Seyfert galaxies (Zamanov et al. 2002, Marziani et al. 2003, Aoki et al. 2005, Boroson 2005, Bian et al. 2005). According to these studies blue outliers have high Eddington ratios and small BLR Balmer line widths. However, not all sources with high Eddington ratios are blue outliers. While Bian et al. (2005) further reported a correlation between blueshift and Eddington ratio of their 7 blue outliers, Aoki et al. (2005) did not find such a correlation for 16 objects. A strong correlation between [OIII] blueshift and [OIII] line width is often seen, and is usually interpreted as evidence for outflows. Zamanov et al. (2002) noticed that most of their blue outliers also show high blueshifts in CIV1549 (but this phenomenon is not exclusive to blue outliers; Sulentic et al. 2007). Aoki et al. (2005) reported a trend that blue outliers have high black hole masses (\(>10^{7}\) M\({}_{\odot}\)). All previous studies of samples of blue outliers focused on the [OIII]-H\(\beta\) spectral region in order to explore the phenomenon, with the exception of Boroson (2005). Although Boroson (2005) measured the positions of other NLR lines in order to establish a systemic reference for the [OIII] line properties, we have, for the first time, measured the widths and strengths of all the optical NLR lines in blue outliers in order to study the nature of blue outliers and explore the dynamics of the NLR. For each galaxy, we find a strong correlation between emission line blueshift and ionization potential of the line-emitting ion. Coincidentally, higher ionization potentials of the ions in question also come with higher critical densities of the forbidden line transitions observed from the respective ions. Therefore, a correlation between outflow velocity and ionization potential would generally imply a correlation with critical density, and vice versa, raising the question which of the two is the fundamental correlation; density stratification or ionization stratification. An important exception to the above rule is [OI]6300, which has zero ionization potential, while its critical density (\(n_{\rm crit}=1.8\,10^{6}\) cm\({}^{-3}\)) is relatively high. [OI] is detected in several of our NLS1 galaxies, and we find that [OI] follows the trend in ionization potential, but not in critical density, arguing that the former correlation is the underlying one (Fig. 3)⁴. We confirm the previously known correlation between [OIII] blueshift and line width. [FOOTNOTE:4][ENDFOOTNOTE] Blue outliers only occur among the NLS1 galaxies of our sample (i.e., sources with high Eddington ratios and small Balmer line widths), but within the NLS1 population, blue outliers do not show a strong correlation with Eddington ratio even though they preferentially avoid low ratios. No correlation of outflow velocity with black hole mass, absolute magnitude, and with the width of the broad component of H\(\beta\) is found. Like in other samples, the number of objects is small, and larger samples of blue outliers are needed to confirm the weak trends. It has occasionally been suggested that [OIII] in blue outliers appears broadened by orientation effects in the sense that we look face-on on the central engine, and into an outflow (Zamanov et al. 2002, Marziani et al. 2003, Boroson 2005). If that scenario is correct, we can use blue outliers as test-beds for orientation-dependent models of NLS1 galaxies which allow for the possibility that the H\(\beta\) line of NLS1 galaxies is narrowed due to viewing angle effects. If, in blue outliers, the BLR was in a plane and if we viewed it face-on, blue outliers should have the smallest H\(\beta\) widths among NLS1 galaxies (here, we temporarily classify NLS1 galaxies independently of their H\(\beta\) width, but only use the ratios [OIII]/H\(\beta\) and FeII/H\(\beta\) which still makes all of our blue outliers NLS1 galaxies: in all cases [OIII]/H\(\beta_{\rm totl}<3\), and FeII/H\(\beta_{\rm totl}>0.5\)). However, we do not find any trend for small widths of the broad Balmer lines among the objects of our sample (see Fig. 4). The [OIII] lines of several objects still show the phenomenon of blue wings, arguing against the previous suggestion that the classical [OIII] emission in blue outliers is absent and we actually only see the blue wing. [However, occasionally, the presence of a strong blue wing could mimic a blue outlier, if the wing is not spectroscopically resolved from the core of the line (e.g., Grandi 1977, Holt et al. 2003)]. ### Models of the narrow-line region There is good evidence that the motion of NLR clouds is strongly influenced by the bulge gravitational potential (e.g., Véron 1981, Whittle et al. 1992, Nelson & Whittle 1996; see the prev. Sect. 4.1). At the same time, there is also evidence for radial motions in NLRs based for instance on blue asymmetries of [OIII] profiles (e.g., de Robertis & Osterbrock 1984, Veilleux 1991, Whittle 1992, Véron-Cetty et al. 2001), on correlations of blue wing blueshift with the Eddington ratio and other arguments (Xu et al. 2007), and on spatially resolved [OIII] velocity shifts (e.g., Schulz 1990, Das et al. 2005). The existence of [OIII] blue wings can formally be equally well interpreted in terms of inflows or outflows, plus selective obscuration. Generally, there is a preference for the outflow interpretation. Regarding theoretical models for outflows, a lot of work has focussed on magnetocentrifugal winds and radiatively driven outflows from the accretion disk region (see Königl 2006, Everett 2007, Proga 2007 for reviews). These models have successfully been applied to BAL flows and the BLR emission lines, are supported by recent observations (Young et al. 2007), and have recently been extended to spatial scales typical of the very inner NLR (Proga et al. 2008). However, little is known about the formation or continuation of such winds on much larger scales on the order of 100 pc – kpc characteristic for NLRs. Mechanisms suggested to be relevant in the NLR (and CLR) include radiation pressure acting on gas (Binette et al. 1997, Das et al. 2007) and on dust grains embedded in the clouds (Binette 1998, Dopita et al. 2002), and the entrainment of NLR clouds in hot winds (Krolik & Vrtilek 1984, Schiano 1986, Mathews & Veilleux 1989, Smith 1993, Everett & Murray 2007). The presence of collimated outflows of radio plasma in form of jets and their local interaction with NLR clouds has been observed directly (e.g., Falcke et al. 1998). Spatially resolved imaging spectroscopy of nearby AGN has produced several good examples of spatial coincidences between radio jets and line blueshifts (e.g., Riffel et al. 2006, Morganti et al. 2007), while in other cases the jet-cloud interaction is very weak and does not significantly affect the local NLR velocity field (e.g., Cecil et al. 2002, Das et al. 2005). In some cases, jets are absent but emission lines are still blueshifted (Barbosa et al. 2008, in prep). In AGN with strong starburst activity winds could also be starburst driven (e.g., Rupke et al. 2005). Regarding NLS1 galaxies, their high Eddington ratios make the presence of radiation-pressure driven _winds_ (on the accretion disk scale) very likely. Less certain and understood is the efficiency of _jet_ launching under high-accretion rate conditions. Again, these mechanisms refer to the innermost AGN region, not to larger scales. Blue outliers with their extreme velocity shifts place particularly tight constraints on models for AGN outflows on large, i.e. NLR, scales. We discuss several NLR models for blue outliers in turn. #### 4.3.1 A compact NLR ? Zamanov et al. (2002) and Marziani et al. (2003) suggested that blue outliers posses a very compact NLR, perhaps the result of the youth of these NLS1 galaxies which did not yet develop a full NLR. Their idea was based on the assumption that blue outliers would only posses [OIII] emission and lack other narrow emission lines. However, we do find a classical NLR in terms of the presence of low-ionization lines. Further, the fact that their [SII] line widths put the blue outliers on the same \(M_{\rm BH}-\sigma\) relation with BLS1 and normal galaxies strongly indicates that their outer NLR is a quiescent classical NLR similar to that of other BLS1 and NLS1 galaxies. #### 4.3.2 A two-component NLR The strong blueshifts we detect in the high-ionization component raises the possibility that we see two independent components; a classical NLR, plus an independent outflow component which could be due to a disk wind, a wind from the torus or in form of a lowly ionized warm absorber. However, this interpretation is very unlikely, because the non-blueshifted [OIII] counterpart to the low-ionization lines, as it would be expected from _the inner part_ of a classical NLR, is weak or absent. This fact leads us almost inevitably to the third and fourth possibility. #### 4.3.3 A classical NLR, modified at small radii The fact that we do not detect a classical inner NLR, in form of a second, non-blueshifted [OIII] emission component, implies that processes directly modify/disturb at least the inner NLR; perhaps in form of radio-jet – cloud interaction. However, the strong dependence of emission line velocity shift on ionization potential that we detect (Fig. 3) indicates that we see a highly stratified, photoionized medium, not a local interaction due to shocks and locally disturbed velocity fields. #### 4.3.4 NLR clouds entrained in a wind The phenomenologically most straight-forward solution is one in which the (CLR and) NLR clouds themselves follow a decelerated outflow. This scenario requires an efficient driving mechanism and perhaps an efficient deceleration mechanism. One possibility is direct acceleration of the NLR clouds by radiation pressure acting on gas or dust; another is the presence of a hot wind which entrains the NLR clouds (see Sect. 4.4). If the wind forms a decelerating outflow, the entrained clouds of the CLR/ inner NLR would have the highest outflow velocities, respectively, which would decrease in dependence of core distance and would leave the outer, low-ionization part of the NLR unaffected. Zamanov et al. (2002) reported a linkage of [OIII] blue-outlierness with broad-line CIV blueshift. Could the same wind persist from the disk, to the high-ionization BLR [but leave the bulk of the BLR unaffected; by blowing perpendicular ?], and on to the CLR and inner NLR ? In this picture, the NLRs of BLS1 galaxies, NLS1s, and blue outliers would be intrinsically similar, and the motion of NLR clouds generally dominated by the bulge gravitational potential. Which emission line regions partake in an outflow would depend on the efficiency/operating distance of the wind. It could be present in all AGN, but would generally only affect the CLR (in AGN with blueshifted iron coronal lines but quiescent NLRs), or level off even before reaching the CLR. ### Mechanisms of cloud acceleration and entrainment While phenomenologically successful, the question is raised as to the origin of the wind/outflow on the one hand, and the entrainment mechanism and cloud stability against disruptive instabilities (Mathews & Veilleux 1989, Schiano et al. 1995) on the other hand. We discuss several possibilities in turn. Cloud acceleration by radiation pressure acting on dustRadiation pressure acting on dust grains embedded in the gas clouds is an efficient way of cloud acceleration (e.g., Binette 1998, Dopita et al. 2002, Fabian et al. 2006). In blue outliers, this mechanism is likely not at work, because we do not expect dust in the high-ionization BLR (we are assuming here that the high-ionization part of the BLR partakes in the outflow, motivated by the results of Zamanov et al. (2002) described in Sect. 4.3.4). Some dust might be present in the CLR (even a small admixture of dust would still lead to efficient radiative acceleration, and generally still predict sufficiently strong gas-phase iron lines; Binette 1998). While, observationally, dust-rich NLRs could be present in individual blue outliers (e.g., RXJ0135\(-\)0043), most of them have very blue optical continua arguing against the presence of an excess of dusty gas along the line of sight. These arguments make cloud acceleration by radiation pressure acting on dust grains an unlikely scenario. Cloud entrainment in collimated radio plasmaOutflowing radio plasma in form of jets is known to be present and to reach large distances from the nucleus in AGN, so could plausibly affect several emission-line regions on its way. The phenomenon of cloud entrainment in radio plasma has been directly observed and studied in starforming regions (Ostriker et al. 2001, Stojimirovic̀ et al. 2006). Jet-cloud interaction can result in a variety of phenomena, including cloud entrainment, jet deflection and disruption and cloud destruction (e.g., Saxton et al. 2005, Krause 2007 and references therein). Of interest here is entrainment (Blandford & Königl 1979, Schiano et al. 1995, Fedorenko et al. 1996). One key problem is cloud longevity against various instabilities. Fedorenko et al. (1996) argued for magnetic NLR confinement which would then allow for NLR cloud entrainment in radio jets. Independent of theoretical considerations the question is raised if the blue outliers of our sample all harbor powerful radio jets. Relatively little is known about the radio properties of NLS1 galaxies in general. On average, they tend to be less radio-loud than BLS1 galaxies (Zhou et al. 2006, Komossa et al. 2006) and share some similarities with compact steep spectrum radio sources (Komossa et al. 2006). Four of the blue outliers of our sample have FIRST radio detections. These imply radio powers of \(P_{\rm 1.4}\)= 10\({}^{22}\)–8 10\({}^{23}\) W Hz\({}^{-1}\) (Tab. 1) at 1.4 GHz; similar to those AGN which Nelson & Whittle (1996) find to be off-set from the \(M_{\rm BH}-\sigma_{*}\) relation. We do not have information on the radio morphology of the blue outliers. Sources are unresolved with FIRST, with one remarkable exception: the radio emission of RXJ0135\(-\)0043 is extended by \(\sim\)10 kpc (or double; see Appendix). Spatially resolved radio observations of the sources are required to search for the presence of jets and to study the radio properties in more detail. Thermal windsVariants of thermal wind models have been studied in order to explain the kinematics of ionized absorbers (Chelouche & Netzer 2005), and of NLRs. _Isothermal_ Parker wind models of Everett & Murray (2007), originally computed in order to model spatially resolved NLR velocity gradients of NGC 4151 (Das et al. 2005), would have roughly the right properties to explain our average blue outlier velocity shifts and radial velocity changes. A range in NLR cloud column densities would lead to a spread in cloud velocities (see Eqn. (10) of Everett & Murray 2007), thereby perhaps explaining the observed line broadening. However, as also shown by Everett & Murray (2007), realistic models including photoionization heating have temperature gradients, and adiabatic cooling decelerates the winds too quickly. An extra heating source of unknown nature would be needed in order to keep the wind isothermal. Models of Das et al. (2007), based on radiative acceleration of NLR clouds, implied that NLR clouds do not decelerate quickly enough in order to explain NLR velocity gradients of NGC 1068 observed with HST; models work after introducing drag forces from an ambient medium. Detailed modeling of the present data would likely involve several of the above model ingredients. Such modelling is beyond the scope of this paper. High Eddington ratios and orientation effectsCommon to blue outliers is their high Eddington ratios. Could high \(L/L_{\rm Edd}\) be the wind driving mechanism ? Additional orientation effects (as also discussed by Marziani et al. 2003, Boroson 2005) are still needed in order to explain why not all AGN with high \(L/L_{\rm Edd}\) are blue outliers. Near face-on orientation would have us look more down the flow in blue outliers, thereby enhancing the stratification, broadening, and blueshift effect. ### Links with (compact) radio sources and mergers It is interesting to point out similarities between the phenomenon of blue outliers in NLS1 galaxies and in radio galaxies (see also Holt et al. 2006). Several radio galaxies show a similar phenomenon of high [OIII] core blueshifts and line broadening (e.g., Tadhunter et al. 2001, Marziani et al. 2003, Holt et al. 2006, Stockton et al. 2007; see Gupta et al. 2005 for a related phenomenon in the UV). Jet-cloud interaction in the (inner) NLR is the favored interpretation of most of these sources. These objects may represent the early stages of radio-source evolution (Tadhunter et al. 2001). Radio galaxies with blue outliers in [OIII] are typically compact flat spectrum sources, are absorbed, and are luminous in the infrared. For some (e.g., PKS1549\(-\)79 and PKS0736+01) there is evidence that we have a near face-on view (Tadhunter et al. 2001, Marziani et al. 2003). As pointed out before, the strong stratification we see in NLS1 blue outliers argues against local jet-cloud interactions in those galaxies, but would be consistent with NLR clouds entrained in the outflowing radio plasma. The blue outliers among the radio galaxies show signs of recent mergers. Regarding NLS1 galaxies in general, there is no evidence that the majority of them underwent recent mergers or has an excess of companion galaxies (Krongold et al. 2001, Ryan et al. 2007). Little is known about the host galaxies of our blue outlier sample, in particular. IRAS11598-0112 indeed is a merger with prominent tidal tails (Veilleux et al. 2002), ultraluminous in the infrared. Inspecting the SDSS images of the other galaxies of our sample we do not find strongly disturbed galaxy images indicating ongoing mergers, but this needs to be confirmed with deeper imaging. One galaxy, RXJ0135\(-\)0043, shows indications of an off-center nucleus. That effect could be caused by interaction, be mimicked by dust, or have another origin. ### Recoiled Black Holes ? Recent simulations of merging black holes predict black hole recoil velocities due to emission of gravitational wave radiation up to several thousand km s\({}^{-1}\) (e.g., Campanelli et al. 2007; review by Pretorius 2007). Potentially, high relative outflow velocities of AGN emission line regions vs the host galaxy can arise if the recoiled black hole keeps its BLR and inner NLR (Bonning et al. 2007). Applied to blue outliers, if they harbored recoiled BHs, their whole BLR (plus the high-ionization NLR) should show high blueshifts, while the ‘remnant’ NLR would still appear in low-ionization lines. In that case, we expect the broad component of the Balmer lines to exhibit the highest blueshifts of all emission lines; which is, however, not observed. Shifts in broad H\(\beta\) are less than those in [OIII]. ### Future work The SDSS data base is well suited for a systematic search for more blue outliers. Zhou et al. (2006) mention in passing the presence of several extreme ones among their NLS1 galaxy sample but do not discuss them further. Spatially resolved optical spectroscopy will allow us to measure directly line widths, outflow velocities, etc. in dependence of the core distance⁵. Spectroscopy in the IR and UV will tell whether trends (a correlation with ionization potential) persist in IR coronal lines and high-ionization UV broad lines. X-ray measurements of blue outliers will be useful to search for signs of high-velocity ionized outflows, and to see whether blue outliers again stick out in AGN correlation space when adding their X-ray properties (X-ray steepness, variability) to correlation analyses. (High-resolution) radio observations of all galaxies will facilitate further comparison between blue outliers in radio galaxies and NLS1 galaxies and will tell whether radio jets are present in NLS1 blue outliers. Radio observations have the potential to confirm the pole-on hypothesis of blue outliers, if relativistic beaming is detected. Imaging with HST will reveal whether the host galaxies of blue outliers show signs of recent mergers. In particular, galaxy merger simulations predict strong outflows in the final merger phase (e.g., Springel et al. 2005). Imaging will allow us to test whether blue outliers are in such a phase. [FOOTNOTE:5][ENDFOOTNOTE] If the face-on interpretation of blue outliers is correct, they are also useful test-beds for the question, whether the width of broad H\(\beta\) is systematically affected by orientation. Increasing the sample size will allow us to test more stringently whether the broad component of H\(\beta\) is systematically narrower in blue outliers. If so, this would imply that BLR clouds are arranged in a plane, and we would underestimate systematically the BH masses in these objects, and perhaps NLS1 galaxies in general. If, instead, their BLR is spherical, we would not see systematically narrower H\(\beta\) in objects viewed face-on, and would not have to worry about correctness of BH mass estimates. Our preliminary results indicate that the latter is the case. On the theoretical side, the question is raised as to which winds can operate across long distances spanning the high-ionization BLR, CLR and a substantial part of the NLR, predict the observed gradient in cloud velocities (\(\sim\)1000 km s\({}^{-1}\) of high-ionization emission-line clouds close to the nucleus, and several hundred km s\({}^{-1}\) further out on typical NLR scales while the outer NLR is mostly unaffected), and ensure longevity of the emission-line clouds. ## 5. Summary and conclusions In [OIII] blue outliers with their extreme velocity shifts the effects of secondary influences on the NLR kinematics are enhanced or dominate completely. Their study is therefore of great relevance for (1) scrutinizing the usefulness and limitations of [OIII] width as a proxy for stellar velocity dispersion; (2) understanding the origin and dynamics of the NLR; (3) investigating driving mechanisms of AGN outflows on large scales; and (4) examining possible links with results from merger simulations which predict that a substantial fraction of the ISM of the merger should be outflowing. We have systematically studied the optical properties of such AGN with high [OIII] blueshifts which deviate from the \(M_{\rm BH}-\sigma_{\rm[OIII]}\) relation of BLS1 and NLS1 galaxies, and obtained the following results: \(\bullet\) All of them have high Eddington ratios (\(L/L_{\rm{edd}}\)=0.5–1.5) and narrow BLR Balmer lines (FWHM(H\(\beta_{\rm b}\))=1200–1800 km s\({}^{-1}\)), which makes them NLS1 galaxies. The fraction of blue outliers among our NLS1 sample is 16% (\(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}150\) km s\({}^{-1}\)), and 5% at the highest outflow velocities (\(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}250\) km s\({}^{-1}\)). While blue outliers do enhance correlations which appear across the whole BLS1-NLS1 population, we do not find strong correlations of [OIII] outflow velocity with the Eddington ratio within the blue outlier population itself; perhaps due to the small sample size. \(\bullet\) We do detect a strong correlation between emission-line blueshift and ionization potential, and confirm a strong correlation between [OIII] blueshift and [OIII] line width. The presence of a classical quiescent _outer_ NLR is indicated by the existence of low ionization lines, by [SII] line widths which locate the blue outliers on the same \(M_{\rm BH}-\sigma_{\rm[SII]}\) relation as other BLS1 and NLS1 galaxies, and by inferred NLR densities similar to other NLS1 galaxies. On the other hand, zero-blueshift [OIII] emission expected from a quiescent _inner_ NLR is weak or absent. \(\bullet\) Taken together, these observations place tight constraints on models: We favor a scenario where NLR clouds of blue outliers are entrained in a decelerating wind. Similar, less powerful winds could be present in all AGN, but would generally only affect the CLR (in AGN with blueshifted iron coronal lines but quiescent NLRs), or level off even before reaching the CLR only affecting the high-ionization BLR. \(\bullet\) The mechanism that drives and decelerates the wind is speculative at present, but could be linked to the high Eddington ratios of the galaxies. Extra orientation effects (near pole-on views), considered previously to explain the correlation of [OIII] blueshift with line width of blue outliers, would also explain the strong ionization stratification we detect. \(\bullet\) Two blue outliers have independent BH mass / stellar velocity dispersion measurements and these place them on or close to the \(M_{\rm BH}-\sigma\) relation of non-active galaxies. This, together with the fact that the width of broad H\(\beta\) does not correlate with [OIII] outflow velocity, indicates: If blue outliers are indeed seen more face-on, this fact does not reflect strongly in their H\(\beta\) widths, implying that their BLR geometry is closer to spherical than to planar. \(\bullet\) Most remarkable among the blue outliers is the galaxy RXJ01354\(-\)0043. Unlike other NLS1 galaxies its radio emission is extended and possibly double, its optical Balmer lines appear to be double-peaked, and its optical spectrum shows strong absorption lines from the host galaxy. The link between blue outliers in NLS1 galaxies and in (compact) radio galaxies needs further exploration. ## 6. Appendix: Notes on individual objects A few sources are included in the SDSS-NLS1 samples of Williams et al. (2002) and Anderson et al. (2003). The high [OIII] blueshifts of SDSSJ115533.50+010730.4 and RXJ01354\(-\)0043 were reported by Bian et al. (2005). Boroson (2005) measured [OIII] blueshifts of NGC450#86, RXJ01354\(-\)0043, PG1244+026, and SDSS17184+5734. Here, we provide a short summary of the multi-wavelength properties of the blue outliers collected from the literature, and give some comments based on our optical spectral analysis. Galaxies are listed in order of decreasing [OIII] blueshift. SBS0919+515This AGN is a known X-ray source, first detected with the Einstein observatory (Chanan et al. 1981), mostly studied in the X-ray regime (e.g., Boller et al. 1996, Vaughan et al. 2001), and optically identified as NLS1 galaxy by Stephens (1989). It shows the highest [OIII] blueshift of our sample (\(v_{\rm[OIII]}=430\) km s\({}^{-1}\)). SDSSJ115533.50+010730.4This AGN was detected in X-rays during the ROSAT all-sky survey (Voges et al. 1999) and was first classified as NLS1 galaxy by Williams et al. (2002). It has the second-highest [OIII] velocity shift of our sample (\(v_{\rm[OIII]}=330\) km s\({}^{-1}\)), highly blueshifted [NeV], and faint coronal line emission of [FeX] with a blueshift corresponding to \(v_{\rm[FeX]}\approx 1000\) km s\({}^{-1}\), among the highest blueshifts reported for coronal lines to date. RXJ01354\(-\)0043 (SDSSJ013521.68\(-\)004402.2)This AGN was detected in the X-ray and radio band (Brinkmann et al. 2000, Wadadekar 2004) and was optically identified as NLS1 galaxy by Williams et al. (2002). It is remarkable in several respects. We find that its optical spectrum appears to be dominated by the host galaxy. Strong absorption lines from higher order Balmer lines, Ca H&K and NaID are detected (Fig. 5). The optical AGN continuum emission is either intrinsically weak, or absorbed (which would require a peculiar geometry of the absorber, given that the broad Balmer lines are present). RXJ01354\(-\)0043 is detected with GALEX⁶ and displays red UV colors. Its (narrow) Balmer lines appear double-peaked, with a separation of \(\sim\)580 km s\({}^{-1}\), or else are affected by residual, exceptionally strong and redshifted, host-galaxy features which is very unlikely, given the strength of H\(\alpha\). The line decomposition shown in Fig. 5 assumes the same widths of the narrow core of H\(\beta\) and of the two [NII] lines, fixed to the width of [SII], and further assumes a fixed [NII] line ratio. The remaining profile was modeled with two Gaussians of free parameters and can be well fit with a broad component plus a second, redshifted relatively narrow component. RXJ01354\(-\)0043 has a FIRST detection with a radio flux of 2 mJy and there is evidence for extended radio emission (Becker et al. 1997⁷), corresponding to a scale of \(\sim\)10 kpc. This is remarkable because few if any NLS1 galaxies are known to have widely extended radio emission (Ulvestad et al 1995, Komossa et al. 2006, Yuan et al. 2008). Inspecting the FIRST image cut-out, the source appears to be double. Among the emission lines, only the Balmer lines appear double-peaked. RXJ01354\(-\)0043 is the first blue outlier to show this phenomenon. Explanations include jet-cloud interaction, a bipolar outflow or, speculatively, superposed strong Balmer absorption (which is rarely seen because the required level population is not easy to achieve; Hall 2007, Lu et al. in prep.). We have used the stellar absorption lines from the host galaxy for a measurement of \(\sigma_{*}\). We obtain \(\sigma_{*}=82\) km s\({}^{-1}\) which is in good agreement with the [SII]-based measurement, \(\sigma_{\rm[SII]}=106\) km s\({}^{-1}\), and locates RXJ01354\(-\)0043 (almost perfectly) on the \(M_{\rm BH}-\sigma_{*}\) relation of non-active galaxies (Fig. 1). [FOOTNOTE:6][ENDFOOTNOTE] [FOOTNOTE:7][ENDFOOTNOTE] NGC450#86Identified as NLS1 galaxy by Williams et al. (2002) and detected in X-rays during the ROSAT all-sky survey (Voges et al. 1999). SDSSJ032606.75+011429.9A basically unknown galaxy, with optical NLS1 spectrum (Williams et al. 2002). No radio or X-ray detection was reported. IRAS 11598\(-\)0112This galaxy is ultraluminous in the infrared (Murphy et al. 1996, Kim & Sanders 1998) with a single nucleus and prominent tidal tails (Veilleux et al. 2002). Its optical spectrum is that of a NLS1 galaxy (Moran et al. 1996). It is almost radio-loud with a 1.4 GHz radio index \(R\approx 5\) (Komossa et al. 2006) and was first detected in X-rays with ROSAT (Voges et al. 1999). The FeII emission in its optical spectrum is not well described by our FeII template. In particular, the ‘red’ and ‘blue’ complexes of FeII do not match each other well, and the source redshift appears to differ from that of FeII. Strong emission of unknown nature remains blueward of [OIII]. Formally, we can describe it with an extra [OIII] component, broad (FWHM([OIII])=1800 km s\({}^{-1}\)) and highly blueshifted (\(v\)=1300 km s\({}^{-1}\)). If real, it could represent an extreme blue wing, or could imply the presence of an extra starburst/shock-driven component. The structure needs to be confirmed by independent spectroscopy. SDSSJ171828.99+573422.3Detected with ROSAT (Brinkmann et al. 1999), and optically identified as NLS1 by Williams et al. (2002). PG1244+026This AGN (Green et al. 1986) is a well-known X-ray, UV, infrared and radio source (e.g., Elvis et al. 1986, Kellerman et al. 1989, Sanders et al. 1989, Fiore et al. 1998, Ballantyne et al. 2001, Jimènez-Bailòn et al. 2005) with an optical NLS1 spectrum (Miller et al. 1992, Veron-Cetty et al. 2001). It is radio quiet with a 5 GHz radio index of \(R=0.5\) (Kellerman et al. 1989). Hayashida (2000) and Czerny et al. (2001) determined its black hole mass based on X-ray variability (the power density spectrum). Czerny et al. (2001) report \(\log M_{\rm{BH}}=5.9\) which is consistent with our value of \(\log M_{\rm{BH}}=6.2\) from applying the relation of Kaspi et al. (2005). We detect in its optical spectrum [FeX] emission with an outflow velocity of 640 km s\({}^{-1}\). RXJ09132+3658Detected in X-rays with ROSAT (Voges et al. 1999, Brinkmann et al. 2000) and in the radio band during the FIRST survey (Becker et al. 1997), and identified as NLS1 galaxy by Xu et al. (1999). DX acknowledges the support of the Chinese National Science Foundation (NSFC) under grant NSFC-10503005, and the support of MPG/MPE. HZ acknowledges support from the Alexander von Humboldt Foundation, from NSFC (grant NSF-10533050), and from program 973 (No. 2007CB815405). LB acknowledges support from CONACyT grant J-50296. We thank our referee for his/her comments and suggestions, and the members of MPE’s new Physics of Galactic Nuclei group and J. Sulentic, D. Proga and D. Merritt for discussions. This research has made use of the SDSS data base, and of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Funding for the SDSS and SDSS II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. ## References * (Abazajian et al. 05) Abazajian, K., et al. 2005, AJ, 129, 1755 * (Anderson et al) Anderson, S.F., et al. 2003, AJ, 126, 2209 * (Aoki et al. 2006) Aoki, K., Kawaguchi, T., & Ohta, K. 2005, ApJ, 618, 601 * (Ballantyne et al. 2001) Ballantyne, D.R., Iwasawa, K., & Fabian, A.C. 2001, MNRAS, 323, 506 * (Barth et al. 05) Barth, A.J., Greene, J.E., & Ho, L.C. 2005, ApJ, 619, L151 * (Becker et al. 1997) Becker, R.H., Helfand, D.J., White, R.L., Gregg, M.D., & Laurent-Muehleisen, S.A. 1997, ApJ, 475, 479 * (Bennert et al. 2006) Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006, A&A, 456, 953 * (Bian et al.) Bian, W., & Zhao, Y. 2004, MNRAS, 347, 607 * (Bian et al.) Bian, W., Yuan, Q., & Zhao, Y. 2005, MNRAS, 364, 187 * (Binette 1998) Binette, L. 1998, MNRAS, 294, L47 * (Binette et al. 1997) Binette, L., Wilson, A.S., Raga, A., Storchi-Bergmann, T., 1997, A&A, 327, 909 * (Blandford and Kenigl 1979) Blandford, R., & Königl, A. 1979, ApL, 20, 15 * (Boller et al. 1996) Boller, T., Brandt, W.N., & Fink, H., 1996, A&A, 305, 53 * (Bonning et al. 2007) Bonning, E.W., Shields, G.A., & Salviander, S. 2007, ApJ, 666, L13 * (Boroson 2002) Boroson, T.A. 2002, ApJ, 565, 78 * (Boroson 2003) Boroson, T.A. 2003, ApJ, 585, 647 * (Boroson 2005) Boroson, T.A. 2005, ApJ, 130, 381 * (Botte et al. 04) Botte, V., Ciroi, S., Rafanelli, P., & Di Mille, F. 2004, AJ, 127, 3168 * (Botte et al. 05) Botte, V., Ciroi, S., Di Mille, F., Rafanelli, P., & Romano, A., 2005, MNRAS, 356, 789 * (Brinkmann et al. 1999) Brinkmann, W., et al. 1999, A&AS, 134, 221 * (Brinkmann et al. 2000) Brinkmann, W., et al. 2000, A&A, 356, 445 * (Campanelli et al. 2007) Campanelli, M., Lousto, C.O., Zlochower, Y., & Merritt, D. 2007, PhRvL, 98, 1102 * (Cecil et al. 2002) Cecil, G., et al. 2002, ApJ, 585, 627 * (Chanan et al. 1981) Chanan, G.A., Margon, B., & Downes R.A. 1981, ApJ, 243, L5 * (Chelouche and Netzer 2005) Chelouche, D., & Netzer, H. 2005, ApJ, 625, 95 * (Churazov et al. 2001) Churazov, E., Brüggen, M., Kaiser, C.R., Böhringer, H. & Forman, W. 2001, ApJ, 554, 261 * (Colbert et al. 1996) Colbert, E.J.M., et al. 1996, ApJS, 105, 75 * (Crenshaw et al. 2007) Crenshaw, D.M., & Kraemer, S.B. 2007, ApJ, 659, 250 * (Czerny et al. 2001) Czerny, B., Nikolajuk, M., Piasecki, M., & Kuraszkiewicz, J. 2001, MNRAS, 325, 865 * (Das et al. 2005) Das, V., et al. 2005, AJ, 130, 945 * (Das et al. 2007) Das, V., Crenshaw, D.M., & Kraemer, S.B. 2007, ApJ, 656, 699 * (de Robertis and Osterbrock 1984) de Robertis, M., & Osterbrock, D.E. 1984, ApJ, 286, 171 * (di Matteo et al. 2005) di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 * (Dopita et al. 2002) Dopita, M., Groves, B.A., Sutherland, R.S., Binette, L., & Cecil, G. 2002, ApJ, 572, 753 * (Elvis et al. 1986) Elvis, M., et al. 1986, ApJ, 310, 291 * (Elvis 2000) Elvis, M. 2000, ApJ, 545, 63 * (Elvis 2006) Elvis, M. 2006, MemSAIt, 77, 573 * (Erkens et al. 1997) Erkens, U., Apenzeller, I., & Wagner, S. 1997, A&A, 323, 707 * (Everett 2007) Everett, J.E. 2007, Ap&SS, 311, 269 * (Everett and Murray 2007) Everett, J.E., & Murray, N. 2007, ApJ, 656, 93 * (Fabian 1999)Fabian, A. 1999, MNRAS, 308, L39 * (Fabian et al. 2006) Fabian, A., Celotti, A., & Erlund, M.C. 2006, MNRAS, 373, L16 * (Falcke et al. 1998) Falcke, H., Wilson, A.S., & Simpson, C. 1998, ApJ, 502, 199 * (Fedorenko et al. 1996) Fedorenko, V.N., Paltani, S., & Zentsova, A.S. 1996, A&A, 314, 368 * (Ferrarese and Merritt 2000) Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 * (Ferrarese and Ford 2005) Ferrarese, L., & Ford, H. 2005, Space Science Reviews, 116, 523 * (Fiore et al. 1998) Fiore, F., et al. 1998, MNRAS, 298, 103 * (Gaskell 1982) Gaskell, C.M. 1982, ApJ, 263, 79 * (Gallimore et al. 2006) Gallimore, J.F., Axon, D.J., O’Dea, C., Baum, S.A., & Pedlar, A. 2006, AJ, 132, 546 * (Gebhardt et al. 00) Gebhardt, K., et al. 2000, ApJ, 539, L13 * (Green et al. 1986) Green, R.F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 * (Greene and Ho 2005) Greene, J.E., & Ho, L.C. 2005, ApJ, 627, 721 * (Grandi 1977) Grandi, S.A. 1977, ApJ, 215, 446 * (Grupe 04) Grupe, D. 2004 AJ, 127, 1799 * (Grupe et al 04) Grupe, D., & Mathur, S. 2004 ApJ, 606, L41 * (Gupta et al. 1995) Gupta, N., Srianan, R., & Saiki, D.J. 2005, MNRAS, 361, 451 * (Hall 2007) Hall, P. 2007, AJ, 133, 1271 * (Hayashida 2000) Hayashida, K. 2000, NewAR 44, 419 * (Heckman et al. 1981) Heckman, T.M., Miley, G.K., van Breugel, W.J.M., & Butcher, H.R. 1981, ApJ, 247, 403 * (Holt et al. 2003) Holt, J., Tadhunter, C.N., & Morganti, R. 2003, MNRAS, 342, 227 * (Holt et al. 2006)Holt, J., et al. 2006, MNRAS, 370, 1633 * (Jimènez-Bailòn et al. 2005) Jimènez-Bailòn, E., et al. 2005, A&A, 435, 449 * (Kaspi et al. 2005) Kaspi, S., et al. 2005, ApJ, 629, 61 * (Kaspi et al. 2000) Kaspi, S., et al. 2000, ApJ, 533, 631 * (Kellermann et al. 1989) Kellermann, K.I., Sramek, R., Schmidt, M., Shaffer, D.B., & Green, R. 1989, AJ, 98, 1195 * (Kim and Sanders 1998) Kim, D.-C., & Sanders, D.B. 1998, ApJS, 119, 41 * (Komossa and Schulz 1997) Komossa, S., & Schulz, H. 1997, A&A, 323, 31 * (Komossa et al. 2006) Komossa, S., et al. 2006, AJ, 132, 531 * (Komossa and Xu 2007) Komossa, S., & Xu, D. 2007, ApJ, 667, L33 (KX07) * (Komossa 2008) Komossa, S. 2008, in: The nuclear region, host galaxy and environment of AGN, E. Benitez, I. Cruz-Gonzales, Y. Krongold (eds), RevMexAA, in press, (arXiv:0710.3326v1) * (Koenigl 2006) Königl, A. 2006, MemSAIt, 77, 598 * (Krause 2007) Krause, M. 2007, NewAR, 51, 174 * (Kriss 1994) Kriss, G.A. 1994, ASP Conf. Series 61, 437 * (Krolik and Vrtilek 1984) Krolik, J.H., & Vrtilek, J.M. 1984, ApJ, 279, 521 * (Krongold et al. 2001) Krongold, Y., Dultzin-Hacyan, D., & Marziani, P. 2001, AJ, 121, 702 * (Krongold et al. 2007) Krongold, Y., et al. 2007, ApJ, 659, 1022 * (Laor et al. 1997) Laor, A., Jannuzi, B.T., Green R.F., & Boroson, T.A. 1997, ApJ, 489, 656 * (Marziani et al. 2003) Marziani, P., Zamanov R.K., Sulentic, J.W., & Calvani, M. 2003, MNRAS, 345, 1133 * (Mathews and Veilleux 1989) Mathews, W.G., & Veilleux, S., 1989, ApJ, 336, 93 * (Mathur et al. 2001) Mathur, S., Kuraszkiewicz, J., & Czerny, B. 2001, NewA, 6, 321 * (Mathur et al. 2005a) Mathur, S., & Grupe, D. 2005a, ApJ, 633, 688 * (Mathur et al. 2005b) Mathur, S., & Grupe, D. 2005b, A&A, 432, 463 * (Miller et al. 1992) Miller, P., Rawlings, S., Saunders, & R., Eales, S. 1992, MNRAS, 254, 93 * (Moll et al. 2007) Moll, R., et al. 2007, A&A, 463, 513 * (Moran et al. 1996) Moran, E.C., Halpern J.P., & Helfand, D.J. 1996, ApJS, 106, 341 * (Morganti et al. 2005) Morganti, R., Tadhunter C.N., & Oosterloo, T.A. 2005, A&A, 444, L9 * (Morganti et al. 2007) Morganti R., Holt, J., Daripalli, L., Oosterloo, T.A., & Tadhunter, C.N. 2007, A&A, in press, [arXiv:0710.1189v1] * (Murphy et al. 1996) Murphy, T.W., et al. 1996, AJ, 111, 1025 * (Nelson 2000) Nelson, C.H. 2000, ApJ, 544, L91 * (Nelson and Whittle 1996) Nelson, C.H., & Whittle, M. 1996, ApJ, 465, 96 * (Netzer and Trakhtenbrot 2007) Netzer, H., & Trakhtenbrot, B. 2007, ApJ, 654, 754 * (Osterbrock 1991) Osterbrock, D.E. 1991, Rep.Prog.Phys. 54, 579 * (Osterbrock and Pogge 1985) Osterbrock, D.E., & Pogge, R. 1985, ApJ, 297, 166 * (Ostriker et al. 2001) Ostriker, E.C., Lee, C.-F., Stone, J.M., & Mundy, L.G. 2001, ApJ, 557, 443 * (Penston et al. 1984) Penston, M.S., Fosbury, R.A.E., Boksenberg, A., Ward, M.J., Wilson, A.S. 1984, MNRAS, 208, 247 * (Phillips 1976) Phillips, M.M. 1976, ApJ, 208, 37 * (Pretorius 2007) Pretorius, F. 2007, arXiv:07101338 * (Proga 2007) Proga, D. 2007, ASP Conf. Ser., 373, 267 * (Proga et al. 2008) Proga, D., Ostriker, J.P., & Kurosawa, R. 2008, ApJ, in press; arXiv:0708.4037v2 * (Rice et al. 2006) Rice, M., et al. 2006, ApJ, 636, 654 * (Riffel et al. 2006) Riffel R.A., Storchi-Bergmann, T., Winge, C., & Barbosa, F.K.B. 2006, MNRAS, 373, 2 * (Rodriguez-Ardila et al. 2006) Rodriguez-Ardila, A., Prieto, M.A., Viegas, S., & Gruenwald, R. 2006, ApJ, 653, 1098 * (Rodriguez Hidalgo et al. 2007) Rodriguez Hidalgo, P., Hamann, F., Nestor, D., & Shields, J. 2007, ASP Conf. Ser. 373, 287 * (Rupke et al. 2005) Rupke, D.S., Veilleux, S., & Sanders, D.B. 2005, ApJ, 632, 751 * (Ryan et al. 2007) Ryan, C.J., de Robertis, M.M., Virani, S., Laor, A., & Dawson, P.C. 2007, ApJ, 654, 799 * (Salviander et al. 2007) Salviander, S., Shields, G.A., Gebhardt, K., & Bonning, E.W. 2007, ApJ, 662, 131 * (Sanders et al. 1989) Sanders, D.B., Phinney, E.S., Neugebauer, G., Soifer, B.T., & Mathews, K. 1989, ApJ, 347, 29 * (Saxton et al. 2005) Saxton, C.J., Bicknell, G.V., Sutherland, R.S., & Midgley, S. 2005, MNRAS, 359, 781 * (Scannapieco et al. 2005) Scannapieco, E., Silk, J., & Bouwens, R. 2005, ApJ, 635, L13 * (Schiano 1986) Schiano, A.V.R. 1986, ApJ, 302, 81 * (Schiano et al. 1995) Schiano, A.V.R., Christiansen, W.A., & Knerr, J.M. 1995, ApJ, 439, 237 * (Schinnerer et al. 1998) Schinnerer, E., Eckart, & A., & Tacconi, L.J. 1998, ApJ, 500, 147 * (Schulz 1990) Schulz, H. 1990, AJ, 99, 142 * (Shields et al. 2003) Shields, G.A., et al. 2003, ApJ, 535, 124 * (Silk and Rees) Silk, J., & Rees, M. 1998, A&A, 331, L1 * (Smith 1993) Smith, S.J. 1993, ApJ, 411, 570 * (Springel et al. 2005) Springel, V., Di Matteo, T., & Hernquist, L. 2005, ApJ, 620, L79 * (Stephens 1989) Stephens, S. 1989, AJ, 97, 10 * (Stockton et al. 1007) Stockton, A., Canalizo, G., Fu, H., & Keel, W. 2007, ApJ, 659, 195 * (Stojimirovic et al. 2006) Stojimirovic̀, I., Narayan, G., Snell, R.L., & Bally, J. 2006, ApJ, 649, 280 * (Sulentic et al. 2007) Sulentic, J., Bachev, R., Marziani, P., Negrete, C.A., & Dultzin, D. 2007, ApJ, 666, 757 * (Tadhunter et al. 2001) Tadhunter, C., Wills, K., Morganti, R., Oosterloo, T., & Dickson, R. 2001, MNRAS, 327, 227 * (Terlevich et al. 1990) Terlevich, E., Diaz, A.I., & Terlevich, R. 1990, MNRAS, 242, 721 * (Tremaine et al. 2002) Tremaine, S., et al. 2002, ApJ, 574, 740 * (Ulvestadt et al. 1995) Ulvestad, J.S., Antonucci, R.R.J., & Goodrich, R.W. 1995, AJ, 109, 81 * (Vaughan et al. 2001) Vaughan, S., Edelson, R., Warwick, R.S., Malkan, M.A., & Goad, M.R. 2001, MNRAS, 327, 673 * (Veilleux 1991) Veilleux, S. 1991, ApJ, 369, 331 * (Veilleux et al. 2002) Veilleux, S., Kim, D.-C., & Sanders, D.B. 2002, ApJS, 143, 315 * (Veilleux et al. 2005) Veilleux, S., Cecil G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 * (Veron 1981) Véron, M.P. 1981, A&A, 100, 12 * (Veron-Cetty et al.)Véron-Cetty, M.P., Véron, P., & Goncalves, A.C. 2001, A&A, 372, 730 * (Veron-catalogue 2003) Véron-Cetty, M.P., & Véron, P. 2003, A&A, 412, 399 * (Veron-Cetty et al.) Véron-Cetty, M.P., Joly, M., & Véron, P. 2004, A&A, 417, 515 * (Voges et al. 1999) Voges, W., et al. 1999, A&A, 349, 389 * (Wadadekar 2004) Wadadekar, Y. 2004, A&A, 416, 35 * (Wandel 2002) Wandel, A. 2002, ApJ, 565, 762 * (Wang and Lu 01) Wang T., & Lu Y. 2001, A&A, 377, 52 * (Watson et al.07) Watson L., Mathur S., & Grupe D. 2007, AJ, 133, 2435 * (Whittle 1992) Whittle, M. 1992, ApJ, 387, 109 * (Williams et al) Williams, R.J., Pogge, R.W., & Mathur, S. 2002, AJ, 124, 3042 * (Wyithe and Loeb 2003) Wyithe, J.S.B., & Loeb. A. 2003, ApJ, 595, 614 * (Xu et al. 1999) Xu, D., Wei, J.Y., & Hu, J.Y. 1999, ApJ, 517, 622 * (Xu et al. 2007a) Xu, D., Komossa, S., Zhou, H., Wang, T., & Wei, J. 2007, ApJ, 670, 60 * (Xu et al. 2008) Xu, D., et al. 2008, AJ, to be submitted * (Young et al. 2007) Young, S., Axon, D.J., Robinson, A., Hough, J.H., & Smith, J.E. 2007, Nat, 450, 74 * (Yuan et al. 2008) Yuan, W., et al. 2008, ApJ, submitted * (Zamanov et al. 2004) Zamanov, R., et al. 2002, ApJ, 576, L9 * (Zhou et al. 06) Zhou, H.-Y., et al. 2006, ApJS, 166, 128 [TABLE:S6.T1][ENDTABLE] [FIGURE:S6.F1][ENDFIGURE] [FIGURE:S6.F2][ENDFIGURE] [FIGURE:S6.F3][ENDFIGURE] [FIGURE:S6.F4][ENDFIGURE] [FIGURE:S6.F5][ENDFIGURE]

# О природе галактик Сейферта с высокими смещениями в сторону синего спектра [OIII]5007 Превратим маркдаун с английского на русский. Сохраняем формулы: S. Комосса Макс-Планк-институт по экстрагалактической физике, Гиссенбахштрассе 1, 85748 Гархинг, Германия; [email protected] Перевод маркдауна с английского на русский. Cохранить формулы: D. Xu Национальные астрономические обсерватории Китайской Академии наук, ул. Датунь, район Чаоян, Пекин, 100012, Китай. H. Чжоу # Макс-Планк-институт по изучению внеземной физики, Гиссенбахштрассе 1, 85748 Гархинг, Германия T. Сторки-Бергманн Институт физики, УФРГС, Кампус ду Вале, КП 15051, Порту-Алегре 91501-970, РС, Бразилия Перевести разметку markdown с английского на русский. Сохранить формулы: L. Binette Отделение физики, физической инженерии и оптики, Лавальский университет, Квебек, Квебек, G1K7P4, Канада; и Институт астрономии, УНАМ, а/я 70-264, 04510 Мехико, ДФ, Мексика. ###### Аннотация Мы изучали свойства галактик Сейферта с большими сдвигами на синюю сторону линии [OIII]5007 ("синие выбросы"), изначально определенные из-за их сильного отклонения от отношения \(M_{\rm BH}-\sigma\) для обычных галактик с нормальными, узкими линиями Сейферта 1 (NLS1) и широкими линиями Сейферта 1 (BLS1). Эти синие выбросы оказываются важными тестовыми площадками для моделей узкой линейной области (NLR), для механизмов привода крупномасштабных оттоков, для связей между галактиками NLS1 и радио-галактиками и для ориентационно-зависимых моделей NLS1. Мы сообщаем о обнаружении сильной корреляции смещения линии с ионизационным потенциалом в каждой галактике, включая измерение корональных линий с радиальными скоростями до 500-1000 км/с, и мы подтверждаем сильную корреляцию между смещением [OIII] и шириной линии. У всех синих выбросов [OIII] имеются узкие ширины их широких линий Бальмера и высокие отношения Эддингтона. В то время как наличие несмещенных низкоионизационных линий указывает на наличие классической внешней неактивной NLR у синих выбросов, мы также сообщаем об отсутствии какой-либо второй, несмещенной по синей составляющей [OIII] от классической внутренней NLR. Эти результаты глубоко ограничивают модели NLR. Мы предпочитаем сценарий, в котором облака NLR затормаживаются в замедляющемся ветре, что объясняет сильную стратификацию и отсутствие нулевого смещения внутренней NLR синих выбросов. Происхождение ветра на данный момент остается спекулятивным (коллимированная радио-плазма, тепловые ветры, радиоактивно ускоренные облака). Он, вероятно, связан с высокими отношениями Эддингтона синих выбросов. Подобные, менее мощные ветра могут быть присутствовать во всех галактиках Сейферта, но обычно они оказывают влияние только на область корональных линий (CLR) или уровняются еще до достижения CLR. Кратко обсуждаются сходства между синими выбросами в галактиках NLS1 и (компактными) радиоисточниками. Заголовки темы: галактики: активные - галактики: эволюция - галактики: индивидуальные (SBS0919+515, SDSSJ115533.50+010730.4, RXJ01354-0043, NGC450#86, SDSSJ032606.75+011429.9, IRAS11598-0112, SDSSJ171828.99+573422.3, PG1244+026, RXJ09132+3658) - галактики: Сейферта - квазары: линии излучения ## 1. Введение Концепция обратной связи из-за выхода имеет потенциальное ключевое значение при понимании коэволюции галактик и черных дыр (Силк и Рис 1998, Фабиан 1999, Уити и Лоуб 2003). Недавние аналитические оценки и симуляции показывают важность обратной связи от ветров/выходов, например, в космическом уменьшении (Сканнапеко и др. 2005), в установлении связи \(M_{\rm BH}-\sigma\) (ди Маттео и др. 2005) и в определении цветов галактик (Спрингел и др. 2005) путем регулирования звездообразования в галактике-хозяйке. Мощные газовые выбросы в активных галактических ядрах (АГН) заливают массу, энергию и металлы в межзвездную среду галактики, а также в межгалактическую среду или внутрикластерную среду (Колберт и др. 1996, Чуразов и др. 2001, Молль и др. 2007). Ветры АГН также играют потенциально важную роль в унифицированных моделях АГН (Элвис 2000, 2006). Cуществуют наблюдательные доказательства оттоков в АГН на различных масштабах и во всех диапазонах волн, начиная от радио (Morganti et al. 2005, Gallimore et al. 2006), до ИК-диапазона (Rodriguez-Ardila et al. 2006), оптического (Das et al. 2005), УФ (Sulentic et al. 2007, Rodriguez Hidalgo et al. 2007, Crenshaw & Kraemer 2007) и рентгеновского диапазона (Chelouche & Netzer 2005, Krongold et al. 2007); см. Veilleux et al. (2005) для обзора. Существуют несколько линий доказательств того, что оттоки особенно сильны в галактиках с узкими линиями Сейферта 1 типа (NLS1). Галактики NLS1 – это подкласс АГН с экстремальными эмиссионными линиями и континуумом, которые, по-видимому, в некоторой степени вызваны их высокими отношениями Эддингтона, низкими массами черных дыр и другими параметрами (например, Osterbrock & Pogge 1985, Boroson 2002, Grupe 2004; см. Komossa 2008 для обзора). Высокие отношения Эддингтона, вероятно, приводят к сильным оттокам, вызванным радиационным давлением. Как класс объектов с низкими массами черных дыр, высокими скоростями аккреции и сильными ветрами, расположение галактик NLS1 на плоскости \(M_{\rm BH}-\sigma\) вызывает особый интерес (Mathur et al. 2001; см. наш Раздел 4.1). Комосса и Су (2007) показали, что галактики NLS1 следуют такому же соотношению \(M_{\rm BH}-\sigma\), как и обычные и широколинейные Сейферта типа 1 (BLS1) галактики, если ширина линий эмиссии [SII]6716,6731 используется в качестве замены для дисперсии скорости звезд. Ширина [OIII]5007 (после удаления асимметричных синих крыльев) все еще является хорошим приближением для дисперсии скорости звезд в галактиках BLS1 и NLS1, с одним важным исключением. Подмножество галактик NLS1 систематически отклоняется от соотношения \(M_{\rm BH}-\sigma\), и все они характеризуются высокими синими смещениями линий [OIII]. В то же время, измерения дисперсии скорости на основе [SII] тех же объектов по-прежнему устанавливают их _на_ соотношение \(M_{\rm BH}-\sigma\) (рис. 1). Таким образом, [OIII] линии этих конкретных галактик не были подходящими для оценки \(\sigma\). Однако, возникает независимый вопрос о том, какой механизм вызывает синие смещения линий [OIII] и что мы можем узнать о них в отношении природы этих систем и, возможно, эволюционного состояния галактик NLS1. Этому вопросу посвящено данное исследование. Ранее была замечена измеримая разница в смещении в красную сторону и ширинах различных линий NLR излучения (обзор Osterbrock 1991). Феномен сильного смещения в синюю сторону [OIII], превышающего сто-несколько сотен км/с (так называемые синие отклонения или blue outliers), является более редким. Он был обнаружен ранее в отдельных объектах (Phillips 1976), но только недавно был систематически изучен (Zamanov et al. 2002, Marziani et al. 2003, Aoki et al. 2005, Boroson 2005, Bian et al. 2005). Эти исследования показали, что у синих отклонений высокие отношения Эддингтона и малые ширины линий Бальмера (все они с FWHM(Hβ) < 4000 км/с и большинство из них с FWHM(Hβ) < 2000 км/с; Marziani et al. 2003). Остается неясным, есть ли (Bian et al. 2005) или нет (Aoki et al. 2005) прямая корреляция между смещением [OIII] в синюю сторону и отношением Эддингтона. Общее для большинства исследований является наличие сильной корреляции между смещением [OIII] в синюю сторону и шириной линии [OIII]. Эта корреляция также известна среди железных корональных линий галактик BLS1 (Penston et al. 1984, Erkens et al. 1997). Причина до сих пор не ясна. Считается, что выбросы играют роль в объяснении этого явления. Кроме Boroson (2005), все исследования выборки сконцентрировались на области [OIII]-H\(\beta\) оптических спектров голубых выбросов, чтобы изучить феномен, в то время как впервые мы включаем информацию со всех обнаруженных оптических линий NLR. Мы сообщаем об обнаружении сильных корреляций и обсуждаем последствия для природы голубых выбросов и для динамических моделей NLR. Эта работа организована следующим образом. В разделе 2 мы описываем выборку и предоставляем детали анализа данных. Результаты тенденций и корреляций представлены в разделе 3, которые затем обсуждаются в разделе 4. В разделе 5 дано краткое изложение и выводы. Некоторые отдельные объекты оказываются замечательными. Заметки о них приведены в приложении. Мы используем космологию с \(H_{\rm 0}\)=70 км с\({}^{-1}\) Мпк\({}^{-1}\), \(\Omega_{\rm M}\)=0.3 и \(\Omega_{\rm\Lambda}\)=0.7 на протяжении всей этой работы. ## 2. Анализ данных ### Пример Девять галактик NLS1 из данной работы были выбраны из выборки Xu и др. (2007, 2008). Исходный выборка и стандартные процедуры сокращения данных были подробно описаны в этой работе. Вкратце, выборка состоит из галактик NLS1 из каталога Верон-Сетти и Верон (2003) и сравнительной выборки галактик BLS1 от Боросона (2003) с красным смещением \(z<0.3\), у которых есть спектры Sloan Digital Sky Survey (SDSS) DR3 (Абазаян и др., 2005) и обнаруженные низкоионные линии (наличие [SII]6716,6731 с S/N\(>\)5). Образцы галактик BLS1 и NLS1 имеют сходные распределения красного смещения и абсолютной величины. Xu и др. (2007) скорректировали спектры SDSS на галактическое затемнение, разложили континуум на составляющие галактики-хозяина и активного ядра (AGN), после чего вычли вклад галактики-хозяина и комплексы FeII из спектров. Профили спектральных линий галактик были аппроксимированы гауссианами с использованием пакета IRAF SPECFIT (Крисс, 1994). Измеренные FWHM были скорректированы на инструментальную расширенность. Переклассификация после аппроксимации спектральных эмиссионных линий привела к 39 BLS1 и 55 NLS1 галактикам в выборке. Мы здесь сосредотачиваемся на девяти галактиках с наибольшими синим смещениями [OIII] (табл. 1), которые были идентифицированы Комоссой и др. (2007; KX07 в дальнейшем). Для сравнения и с целью выявления тенденций во всей популяции BLS1 - NLS1 - синих выбросов, показаны результаты для полной выборки NLS1 (и BLS1). Когда мы сообщаем измерения оптической силы FeII (FeII4570), это интегрированный поток эмиссионного комплекса FeII между длиной волн отдохновения 4434 Å и 4684 Å. Мы называем суммарный поток двух сернистых линий, [SII]6716 и [SII]6731, [SII]6725. ### Подгонка эмиссионной линии и профиль [OIII] Линии Бальмера были разложены на три компоненты: узкое ядро (H\(\beta_{\rm n}\); FWHM фиксировано на основе [SII]6716,6731), а также две широкие компоненты. Двум широким компонентам не придается физического значения; они служат лишь математическим описанием (см. Xu et al. 2008 для альтернативной аппроксимации Лоренцом). Ширина широкой компоненты эмиссии линии H\(\beta_{\rm b}\) определяется как FWHM суммы двух гауссиан. С исключением [OIII], запрещенные линии хорошо описываются одним гауссовым профилем. Общий профиль эмиссии [OIII], [OIII]\({}_{\rm totl}\), был разложен на две гауссовы компоненты: узкое ядро ([OIII]\({}_{\rm c}\)) и широкую основу. Мы различаем два типа спектральной сложности [OIII]: (1) наличие широкой основы, которая часто имеет синюю асимметрию (например, Heckman et al. 1981) и называется "синим крылом", и (2) систематическое смещение всего ядра [OIII] в сторону синего. Объекты, в которых наблюдается последний феномен, называются "синими выбросами" (Zamanov et al. 2002)¹. Измерения FWHM и смещения в сторону синего для [OIII], приведенные в этой работе, относятся к ядру линии эмиссии, если не указано иное. [FOOTNOTE:1][ENDFOOTNOTE] - перевести форматирование из Markdown на русский. Сохранить формулы. В идеале, измерения скоростного сдвига [OIII] следует выполнять относительно покоя галактики, который определяется поглощением звездными линиями поглощения от галактики-хозяина. Однако, эти особенности обычно слабы или отсутствуют в наших галактиках (и в галактиках NLS1 в целом). Поэтому мы измеряем скоростные сдвиги [OIII] и всех остальных линий относительно [SII]. Мы используем положительные значения скорости для обозначения синих смещений и отрицательные - для красных смещений. Смещения линий H\(\beta\) и других низко-ионных линий ([OI]6300, NII[6584], [OII]3727) хорошо согласуются с [SII], в то время как другие высоко-ионные линии ([NeIII]3861, [NeV]3426 и железные корональные линии) характеризуются высокими синим смещением (Раздел 3.3). Если линии слишком слабы, чтобы их можно было аппроксимировать гауссовым распределением с произвольной шириной, мы использовали заданную ширину (заданную FWHM([SII]) для низкого ионизирования и заданную FWHM([OIII]\({}_{\rm c}\)) для высокого ионизирования), и определяли центральную длину волны для измерения синего смещения. Результаты приведены в Табл. 1. Поскольку красные смещения, предоставленные трубопроводом SDSS, определены на основе всех сильно обнаруженных линий излучения и, следовательно, подвержены синему смещению [OIII], мы повторно измерили красные смещения на основе H\(\beta_{\rm n}\). Именно эти значения красного смещения приведены в Табл. 1. Мы измерили средние отношения [OIII]\({}_{\rm totl}\)/[SII]6725 в нашей выборке галактик BLS1 и NLS1. Мы обнаружили, что в терминах этого отношения их NLR-ы схожи, с \(<\)[OIII]\({}_{\rm totl}\)/[SII]6725\(>\)=5 в галактиках BLS1 и \(<\)[OIII]\({}_{\rm totl}\)/[SII]6725\(>\)=4 в галактиках NLS1. Заметки по отдельным объектам приведены в Приложении. Здесь мы кратко комментируем обнаружение [FeX]6375 в двух голубых выбросах. В PG1244+026 [FeX] смешивается с [OI]6365. При декомпозиции ширина [OI]6365 была фиксирована как у [OI]6300. Двукомпонентное соотношение затем воспроизводит ожидаемое соотношение [OI]6300/[OI]6365 \(\approx\) 3. [FeX] сдвигается в синюю сторону на 640 км/с. В RXJ0135\(-\)0043, [FeX] перекрывается с атмосферным O\({}_{2}\), который неидеально скорректирован. Поэтому ширина [FeX] была фиксирована как у [OIII]. Это дает скорость оттока 990 км/с. ### Устойчивость спектральных аппроксимаций: разложение непрерывного и линейного спектра Чтобы увидеть, насколько процедура подгонки влияет на измерения потоков, асимметрий и сдвигов [OIII], мы повторили спектральный анализ несколько раз при различных условиях и предположениях: Мы подгоняли спектр с учетом коррекции галактического хозяина и вычитания FeII, а для сравнения также использовали исходный спектр SDSS без этих исправлений. Мы повторно подогнали профиль [OIII] различными способами и различными гауссовыми разложениями. Профиль [OIII] подгонялся только по красной половине профиля, или различными долями от общего профиля, или только верхними 30% профиля, или с использованием однокомпонентного и двухкомпонентного гауссова профиля. Подгонка профиля с использованием одной единственной компоненты гауссиана максимизирует сдвиг в объектах с значительными синими крыльями [OIII]. Во всех остальных случаях неопределенности в сдвиге линии из-за невычитания вклада галактического хозяина и из-за различных процедур подгонки линии, как правило, намного меньше 50 км с\({}^{-1}\). Сдвиг, определенный независимо по более слабой линии [OIII]4959, также согласуется с [OIII]5007 с точностью лучше, чем на 50 км с\({}^{-1}\). Четыре из наших галактик также присутствуют в выборке Боросона (2005). Его измерения сдвига [OIII] синего согласуются с нашими с точностью, как правило, лучше \(\pm\)10 км с\({}^{-1}\). Неопределенность в полной ширине на полувысоте (FWHM) ядра [OIII] обычно составляет 30% для [OIII] линий с дополнительным синим крылом (меньше для остальных) и возникает из-за неопределенности в разложении. Заметим, что частота появления синих крыльев [OIII] у объектов с синим отклонением ни выше, ни ниже среднего значения (см. также Боросон 2005). ## 3. Результаты ### Ограничения на наличие / отсутствие смещения в синюю сторону линий излучения Для облегчения систематического обсуждения моделей NLR синих выбросов (см. разд. 4.3), мы исследовали, имеет ли неперемещенная низкоионизационная линия (хотя и слабая) контрпару (высокоионизационную [OIII]), и наоборот². Мы сделали это представительно для трех галактик с наибольшим синим сдвигом [OIII] (SBS0919+515, SDSSJ11555+ 0107 и RXJ01354\(-\)0043), а также для галактики с наивысшим S/N (PG1244+026). Мы рассмотрели следующие три вопроса: [FOOTNOTE:2][ENDFOOTNOTE] - переведите это предложение на русский язык. (1) Есть ли в спектре какая-либо эмиссия [OIII] при нулевом смещении в сторону синего? (которая может происходить от внутреннего NLR; или быть контрподчетом низкоионизационных линий эмиссии из внешнего NLR)? Для проверки этого мы добавили дополнительный гауссовый вклад в линию [OIII] при нулевом смещении в сторону синего (или при \(v_{\rm[OIII]}=50\) км/с, среднее значение нашей выборки NLS1, исключая синие выбросы) и с фиксированной FWHM([OIII]\({}_{\rm extra}\))=FWHM([SII]). Мы обнаружили, что если она присутствует, то она должна быть очень слабой. Среднее отношение [OIII]\({}_{\rm totl}\)/[SII]6725 в нашей выборке BLS1 составляет 5, в то время как в нашей выборке NLS1 оно составляет 4. Это значение 4 гораздо выше верхнего предела дополнительной компоненты, которая была подогнана к наблюдаемым спектрам: Обычно, [OIII]\({}_{\rm extra}\)/[SII]6725 \(\approx 0.1-0.4\), и всегда, [OIII]\({}_{\rm extra}\)/[SII]6725 \(<1\). Поскольку соотношение [OIII]/[SII] в ближних галактиках Сейферта обычно уменьшается с увеличением радиуса (в моделях и наблюдениях; Комосса и Шульц 1997, Беннерт и др. 2006) и поскольку должен быть вклад [OIII] от внешних облаков, испускающих [SII], предельные значения для любого несмещенного в области синего [OIII] вклада из _внутреннего_ NLR очень жесткие. (2) Имеет ли сине-смещенный [OIII] контрпарт в виде сине-смещенного Н\(\beta\) ? То есть, насколько сильно сине-смещенный Н\(\beta\) мог быть "скрыт" в профиле Н\(\beta\)? Для проверки этого мы повторно подогнали профиль Н\(\beta\), добавив дополнительную гауссову компоненту с параметрами этой дополнительной компоненты, фиксированными на значениях \(v_{\rm H\beta_{extra}}=v_{\rm[OIII]_{c}}\), FWHM(H\(\beta_{\rm extra}\))=FWHM([OIII]\({}_{\rm c}\)) и соотношение интенсивностей [OIII]\({}_{\rm c}\)/H\(\beta_{\rm extra}\)=10. Мы обнаружили, что такая слабая компонента в общем случае может быть скрыта в профиле Н\(\beta\). (3) Имеет ли смещение в синюю сторону линия [OIII] смещенную в синюю сторону низкокионизационную пару [SII]? Это не так. Для типичных _средних по пространству_ отношений [OIII]/[SII]6725 \(\approx\)4 в нашей выборке NLS1, синие линии [SII] в общем случае должны были быть обнаружены, но отсутствуют. Очень слабые смещенные в синюю сторону линии [SII], возникающие, возможно, во внутренней NLR, не могут быть исключены с использованием имеющихся данных. Вкратце, мы обнаружили (1) мало доказательств нулевого синего смещения излучения [OIII] (количество излучения, соответствующее спектрам, вероятно, происходит из внешних частей NLR, которая также излучает в [SII] и других низкоионизационных линиях); (2) дополнительная сине-смещенная компонента в H\(\beta\) - ожидаемый аналог сине-смещенного [OIII] - может быть скрыта в профиле H\(\beta\); и (3) в низкоионизационных линиях не обнаружено высокосмещенной компоненты. ### Оценки масс черных дыр, отношений Эддингтона и плотностей NLR Массы черных дыр были оценены с использованием соотношения радиуса (\(R_{\rm BLR}\))-люминозности (\(L\)) галактик BLS1, сообщенного Каспи и др. (2005), и ширины линии H\(\beta\). Люминозности при 5100Å были взяты из работы Сю и др. (2008) и основаны на поправленных магнитудах SDSS g* и r* с учетом Галактического поглощения. Поскольку у нас отсутствуют многоволновые спектральные энергетические распределения, болометрическая луминозность \(L_{\rm bol}\) была оценена с использованием стандартной болометрической поправки \(L_{\rm bol}=9\,\lambda{L_{\rm 5100}}\) (Каспи и др., 2000). \(L_{\rm Edd}\) был вычислен из массы черной дыры согласно \(L_{\rm Edd}=1.3\,10^{38}\) M\({}_{\rm BH}\)/M\({}_{\odot}\) эрг/с. Типичные ошибки в индивидуальных оценках массы черной дыры могут достигать 0,5 dex и обусловлены использованием данных с одного эпохи, неопределенностями в декомпозиции H\(\beta\) и вкладе галактики-хозяйки. Плотность NLR была получена из отношения интенсивности [SII], чувствительного к плотности, [SII]6716/[SII]6731 (Сю и др., 2007). ### Тенденции и корреляции Мы проверили (1) тенденции скорости истечения с другими (атомными) параметрами в каждом отдельном спектре, и (2) тенденции в нашем образце синих выбросов (имеют ли все синие выбросы высокие соотношения Эддингтона, высокие массы черных дыр и т. д.?), и (3) тенденции в нашем общем образце галактик BLS1 и NLS1. #### 3.3.1 Сильная корреляция сдвига линии с ионизационным потенциалом Мы обнаружили сильную корреляцию между смещением эмиссионной линии в синюю сторону и ионизационным потенциалом (рис. 3). В то время как линии низкой ионизации [OI], [OII] и [NII], а также Бальмеровские линии H\(\alpha\) и H\(\beta\) имеют очень похожую скорость с [SII], линии высокой ионизации, с другой стороны, демонстрируют сильное смещение в синюю сторону, которое увеличивается с ионизационным потенциалом. Две галактики (SDSSJ115533.50+010730.4 и PG1244+026) показывают экстремальные смещения в синюю сторону в [Fe X], порядка 600-1000 км с\({}^{-1}\). Также есть корреляция между скоростью оттока и критической плотностью для отдельных переходов линий (рис. 3), но она менее четкая в том смысле, что [OI]6300, у которой низкий ионизационный потенциал, но высокая критическая плотность, не следует этой тенденции. #### 3.3.2 Тенденции и корреляции смещения в синюю сторону [OIII] с параметрами линии и галактики Мы скоррелировали смещение спектральных линий [OIII] (для синих выбросов и для всей выборки) с различными параметрами линий (ширина линии, отношение интенсивностей) и свойствами галактик (абсолютная величина, масса центральной черной дыры, отношение Эддингтона, плотность NLR). Сильнейшая корреляция наблюдается между смещением [OIII] и шириной линии [OIII] (коэффициент корреляции Спирмена \(r_{\rm S}\)=0.6 для всей выборки NLS1 и еще более высокий для синих выбросов; рис. 3). Внутри выборки NLS1 есть тенденция, согласно которой синие выбросы предпочитают избегать низких отношений Эддингтона \(L/L_{\rm edd}\) и низких отношений FeII/H\(\beta\). Большинство синих выбросов имеют небольшие значения отношения [OIII]/H\(\beta_{\rm totl}\). Мы не обнаружили тенденций противотечной скорости относительно плотности NLR \(n_{\rm e}\), массы черной дыры, абсолютной величины \(M_{\rm i}\) и ширины широкой компоненты H\(\beta\) (рис. 4). Однако, хотя тенденции отсутствуют внутри самих NLS1, интересно отметить, что присутствие синих выбросов усиливает тенденции, которые становятся заметными, когда галактики BLS1 добавляются к графикам корреляции (рис. 4). ### Частота синих выбросов Среди нашей выборки синие выбросы встречаются только в галактиках NLS1. При скорости \(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}150\) км с\({}^{-1}\) доля синих выбросов составляет 16%. Если вместо этого использовать скорость \(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}250\) км с\({}^{-1}\), как в работе Заманова и др. (2002), доля синих выбросов среди галактик NLS1 составляет 5%. ## 4. Обсуждение ### Локус Сейфертских галактик с синими сдвигами [OIII] на плоскости \(M_{\rm BH}-\sigma\) Исследование расположения различных типов галактик на плоскости \(M_{\rm BH}-\sigma\) и их потенциальной эволюции на этой плоскости представляет большой интерес в контексте моделей формирования и эволюции галактик. В AGN часто сложно измерить скорость дисперсии звезд, и ширина [OIII] стала удобным приближенным показателем скорости дисперсии звезд (например, Terlevich et al. 1990, Whittle 1992, Nelson & Whittle 1996, Nelson 2000, Shields et al. 2003, Boroson 2003, Greene & Ho 2005, Netzer and Trakhtenbrot 2007, Salviander et al. 2007) после исключения синих крыльев [OIII] и исключения галактик с мощными радиоисточниками линейного масштаба килопарсек. Разброс в зависимости больше, чем в исходной зависимости \(M_{\rm BH}-\sigma_{*}\) (Ferrarese & Merritt 2000, Gebhardt et al. 2000) и указывает на вторичное влияние на кинематику газа (например, Nelson & Whittle 1996, Rice et al. 2006). Mathur et al. (2001) указали на важность изучения сосредоточения галактик NLS1 на плоскости \(M_{\rm BH}-\sigma\), что стало целью ряда последующих исследований (Wang & Lu 2001, Wandel 2002, Botte et al. 2004, 2005, Bian et al. 2004, Grupe & Mathur 2004, Barth et al. 2005, Greene & Ho 2005, Mathur & Grupe 2005a,b, Zhou et al. 2006, Ryan et al. 2007, Watson et al. 2007, Komossa & Xu 2007). Любое такое исследование включает один важный шаг: различение настоящих выбросов из отношения \(M_{\rm BH}-\sigma\) с одной стороны и видимых выбросов с другой стороны. Видимые выбросы будут отличаться от отношения \(M_{\rm BH}-\sigma\), поскольку либо выбор ширины линии в качестве меры дисперсии скоростей звезд был неподходящим, либо выбор параметров линии и непрерывного спектра в качестве меры массы черной дыры был неподходящим. KX07 показали, что те галактики NLS1 из их выборки, которые значительно отклоняются от отношения \(M_{\rm BH}-\sigma\) у обычных (и BLS1) галактик, все характеризуются высокими сдвигами в синюю сторону [OIII]. В то время как эти линии [OIII] не были подходящими в качестве замены для дисперсии скоростей звезд, замеры скоростей от СIИ на тех же объектах всё же позволяли разместить их на отношении \(M_{\rm BH}-\sigma\). Почти все галактики, которые наиболее сильно отклоняются от отношения \(M_{\rm BH}-\sigma\) (см. нашу Рис. 1), показывают \(v_{\rm[OIII]}>150\) км с\({}^{-1}\). Эти шесть объектов, плюс три дополнительных, которые также показывают \(v_{\rm[OIII]}>150\) км с\({}^{-1}\), определяют девять синих выбросов, которые являются целью данного исследования. Для того чтобы систематически измерить отклонение галактики от отношения \(M_{\rm BH}-\sigma_{*}\), мы определяем величину \(\Delta\sigma:=\log\sigma_{obs}-\log\sigma_{pred}\) (как в KX07), где \(\sigma_{obs}\) - наблюдаемое смещение эмиссионной линии, а \(\sigma_{pred}\) - предсказанное распределение скоростей звезд по отношению \(M_{\rm BH}-\sigma_{*}\) Феррарезе и Форда (2005). Мы обнаруживаем сильную корреляцию между смещением [OIII] и \(\Delta\sigma\) (рис. 1). Это обнаружение демонстрирует, что систематическое смещение скорости [OIII] влияет на отклонение объекта от отношения \(M_{\rm BH}-\sigma\) (см. также Боросон 2005). Мы также обнаруживаем, что корреляция между \(L/L_{\rm Edd}\) и \(\Delta\sigma\) (например, Матур и Групе 2005, Грин и Хо 2005; см. также Нетцер и Трахтенброт 2007) присутствует только в нашей выборке, если мы включаем синие отклонения; когда они исключаются из выборки, корреляция отсутствует (последняя панель нашего рис. 4, см. также KX07). У двух из наших NLS1-всплесков-синих погрешности массы барионных чёрных дыр оцениваются независимо. Из рентгеновской изменчивости Czerny и соавт. (2001) оценили \(\log M_{\rm BH} = 5.9\) для PG1244+062, что хорошо согласуется с нашей оценкой, полученной с применением связи \(R_{\rm BLR} - L\) (\(\log M_{\rm BH} = 6.2\)). Для RX01354-0043 мы непосредственно измерили \(\sigma_{*}\) с помощью поглощения света звезд (см. Приложение). Это значение хорошо согласуется с \(\sigma_{\rm[SII]}\) и практически точно помещает RXJ01354-0043 на связь массы барионной чёрной дыры и дисперсии скорости \(\sigma_{*}\) (рис. 1). Эти результаты демонстрируют важность измерения сдвига к синему в [OIII], а также исключения объектов с высокими сдвигами из выборки перед установлением соотношения \(M_{\rm BH}-\sigma_{\rm[OIII]}\). Возникает независимый вопрос о том, что может вызывать сдвиги к синему в случае этих выбросов [OIII]. ### Синие выбросы: тенденции и корреляции Феномен незначительного синего сдвига и ширины линий излучения NLR был признан с тех пор, как была разработана спектроскопия AGN, и обычно он связывается с определенным стратификацией NLR в том смысле, что линии высокой ионизации предпочтительно образуются на малых расстояниях от ядра, в то время как линии низкой ионизации образуются предпочтительно на больших радиусах (например, Osterbrock 1991). Присутствие сильного синего сдвига [OIII] порядка нескольких сотен км с\({}^{-1}\) было замечено ранее в прототипической галактике NLS1 IZw1³ (например, Phillips 1976, Véron-Cetty et al. 2004). Галактика также показывает очень синий сдвиг ИК корональных линий (Schinnerer et al. 1998) и синий сдвиг УФ линий высокой ионизации (Laor et al. 1997). [FOOTNOTE:3][ENDFOOTNOTE] - [ССЫЛКА-СНИЗУ:3][КОНЕЦ-ССЫЛКИ-СНИЗУ:3] Несколько последних исследований систематически рассмотрели явление голубых выбросов в больших выборках галактик типа 1 Сейферта (Заманов и др., 2002, Марциани и др., 2003, Аоки и др., 2005, Боросон, 2005, Биань и др., 2005). Согласно этим исследованиям, голубые выбросы имеют высокие отношения Эддингтона и небольшие ширины линии Бальмера в области широкой линии региона. Однако не все объекты с высокими отношениями Эддингтона являются голубыми выбросами. Биань и др. (2005) также сообщили о корреляции между сдвигом в сторону голубого и отношением Эддингтона из 7 их голубых выбросов, тогда как Аоки и др. (2005) не обнаружили такой корреляции для 16 объектов. Часто наблюдается сильная корреляция между сдвигом в сторону голубого в линии [OIII] и шириной этой линии, которая обычно толкуется как доказательство выбросов. Заманов и др. (2002) заметили, что у большинства их голубых выбросов также наблюдаются высокие сдвиги в сторону голубого в CIV1549 (но это явление не является исключительным для голубых выбросов; Сулентик и др., 2007). Аоки и др. (2005) сообщили о тенденции, что у голубых выбросов высокие массы черных дыр (\(>10^{7}\) M\({}_{\odot}\)). Все предыдущие исследования выборок голубых выбросов сфокусировались на спектральной области [OIII]-H\(\beta\) для изучения явления, за исключением Боросона (2005). Хотя Боросон (2005) измерял положения других линий РНЛ для установления системного опорного значения свойств линии [OIII], мы впервые измерили ширины и интенсивности всех оптических линий РНЛ у голубых выбросов для изучения природы голубых выбросов и исследования динамики РНЛ. Для каждой галактики мы обнаружили сильную корреляцию между смещением линии излучения в синюю сторону и ионизационным потенциалом иона, излучающего линию. Совпадение высоких ионизационных потенциалов ионов вопроса также приводит к более высоким критическим плотностям запрещенных переходов линий, наблюдаемых от соответствующих ионов. Следовательно, корреляция между скоростью оттока и ионизационным потенциалом, как правило, подразумевает корреляцию с критической плотностью, и наоборот, возникает вопрос, какая из них является фундаментальной корреляцией: стратификация плотности или стратификация ионизации. Важным исключением из вышеуказанного правила является [OI]6300, у которого нулевой ионизационный потенциал, в то время как его критическая плотность (\(n_{\rm crit}=1.8\,10^{6}\) см\({}^{-3}\)) относительно высока. [OI] обнаруживается в нескольких из наших галактик NLS1, и мы обнаружили, что [OI] следует тенденции ионизационного потенциала, но не критической плотности, что подтверждает, что первоявляющаяся корреляция и является подлежащей (рис. 3)⁴. Мы подтверждаем ранее известную корреляцию между синевым смещением [OIII] и шириной линии. [FOOTNOTE:4][ENDFOOTNOTE] [ССЫЛКА_В_СУБПИСИ:4] Синие выключения встречаются только среди галактик типа NLS1 из нашей выборки (то есть источников с высокими отношениями Эддингтона и малыми ширинами линий Бальмера), но среди популяции NLS1 синие выбросы показывают слабую корреляцию с отношением Эддингтона, хотя они предпочитают избегать низких коэффициентов. Не найдено никакой корреляции скорости выброса с массой черной дыры, абсолютной звездной величиной и шириной широкой компоненты H(\β). Как и в других выборках, количество объектов невелико, и требуются более крупные выборки синих выбросов для подтверждения слабых тенденций. Иногда предлагается, что [OIII] в синих выбросах уширяется ориентационными эффектами в том смысле, что мы смотрим на центральный двигатель с фронтальной стороны и на отток (Заманов и др. 2002, Марциани и др. 2003, Борозон 2005). Если эта сценарий является верным, мы можем использовать синие выбросы в качестве тест-площадок для ориентационно-зависимых моделей галактик NLS1, которые предусматривают возможность узкого H\(\beta\) линии галактик NLS1 из-за эффектов угла обзора. Если БЛР в синих выбросах находится в плоскости и мы смотрим на нее с фронтальной стороны, синие выбросы должны иметь наименьшие ширины H\(\beta\) среди галактик NLS1 (здесь мы временно классифицируем галактики NLS1 независимо от их ширины H\(\beta\), но используем только отношения [OIII]/H\(\beta\) и FeII/H\(\beta\), что все равно делает все наши синие выбросы галактиками NLS1: во всех случаях [OIII]/H\(\beta_{\rm totl}<3\), и FeII/H\(\beta_{\rm totl}>0.5\)). Однако мы не обнаруживаем тенденции к маленьким ширинам широких Вальмеровских линий среди объектов нашей выборки (см. рис. 4). [Sonic: ОIII] линии нескольких объектов по-прежнему проявляют феномен синих крыльев, что указывает на то, что классическая [Sonic: ОIII] эмиссия у синих выбросов отсутствует, и на самом деле мы видим только синее крыло. [Однако иногда наличие сильного синего крыла может имитировать синий выброс, если край линии не спектроскопически разрешен от ядра (например, Гранди 1977, Холт и др. 2003)]. ### Модели узкой линейной области Существуют убедительные доказательства того, что движение облаков NLR сильно подвержено гравитационному потенциалу толстой части (например, Верон 1981, Уиттл и др. 1992, Нельсон и Уиттл 1996; см. предыдущий раздел 4.1). В то же время есть также доказательства радиального движения в NLR, основанные, например, на синих асимметриях профилей [OIII] (например, де Робертис и Остерброк 1984, Вейле 1991, Уиттл 1992, Верон-Сетти и др. 2001), на корреляции синего сдвига крыла с соотношением Эддингтона и другими аргументами (Xu и др. 2007) и на пространственно разрешенных [OIII] сдвигах скорости (например, Шульц 1990, Дас и др. 2005). Существование синих крыльев [OIII] формально может быть одинаково хорошо интерпретировано в терминах притоков или выталкиваний, плюс выборочной затененности. В целом предпочтение отдается интерпретации выталкивания. Относительно теоретических моделей для оттоков, много работы было сосредоточено на магнетоцентробежных ветрах и радиативно-движимых оттоках из области аккреционного диска (см. Königl 2006, Everett 2007, Proga 2007 для обзоров). Эти модели успешно применялись к потокам BAL и спектральным линиям BLR, получили подтверждение в недавних наблюдениях (Young et al. 2007) и недавно были расширены на пространственные масштабы, типичные для очень внутренней области NLR (Proga et al. 2008). Однако мало что известно о формировании или продолжении таких ветров на гораздо больших пространственных масштабах, порядка 100 пк - кпк, характерных для NLRs. Механизмы, предлагаемые быть значимыми в NLR (и CLR), включают давление излучения на газ (Binette et al. 1997, Das et al. 2007) и на пылевые зерна, находящиеся в облаках (Binette 1998, Dopita et al. 2002), и увлечение облаков NLR горячими ветрами (Krolik & Vrtilek 1984, Schiano 1986, Mathews & Veilleux 1989, Smith 1993, Everett & Murray 2007). Непосредственное наблюдение показало наличие узконаправленных оттоков радиоплазмы в виде струй и их локальное взаимодействие с облаками NLR (например, Falcke et al. 1998). Пространственно разрешенная изображающая спектроскопия близлежащих AGN привела к нескольким хорошим примерам пространственных совпадений между радиоструями и смещением линии (например, Riffel et al. 2006, Morganti et al. 2007), в то время как в других случаях взаимодействие струи с облаками очень слабое и не оказывает существенного влияния на местное значение скорости NLR (например, Cecil et al. 2002, Das et al. 2005). В некоторых случаях отсутствуют струи, но линии испускания все равно смещены в синюю сторону (Barbosa et al. 2008, в печати). В AGN с выраженной звездообразной активностью ветра также могут быть вызваны звездообразной активностью (например, Rupke et al. 2005). Относительно галактик NLS1, высокое отношение Эддингтона делает очень вероятным наличие _ветров_, приводимых излучением (на масштабах аккреционного диска). Меньше известна и понимается эффективность запуска _струй_ при условиях высокой аккреции. Опять же, эти механизмы относятся к самому внутреннему региону АГН, а не к более крупным масштабам. Синие выбросы со своими экстремальными смещениями скорости ставят особо жесткие ограничения на модели выталкивания АГН на большие масштабы, то есть на масштабы NLR. Мы обсуждаем несколько моделей NLR для синих выбросов по очереди. #### 4.3.1 Компактный НЛР ? Zamanov и др. (2002) и Marziani и др. (2003) предположили, что синие выбросы обладают очень компактным NLR, возможно, это результат молодости этих галактик NLS1, которые еще не развили полноценный NLR. Их идея была основана на предположении, что синие выбросы будут иметь только [OIII] излучение и не будут обладать другими узкими линиями излучения. Однако, у нас действительно есть классический NLR с точки зрения наличия низкоионизационных линий. Кроме того, факт того, что ширина линий [SII] ставит синие выбросы на одинаковое \(M_{\rm BH}-\sigma\) отношение с BLS1 и обычными галактиками, крепко указывает на то, что их внешний NLR является спокойным классическим NLR, подобным другим галактикам BLS1 и NLS1. #### 4.3.2 Двухкомпонентный NLR Сильное сдвигание в синюю сторону, которое мы обнаруживаем в компоненте с высокой ионизацией, поднимает возможность того, что мы видим две независимые компоненты: классическую NLR и независимую компоненту оттока, которая может быть вызвана вихрем диска, струей из тора или в форме слабоионизированного теплого поглотителя. Однако, данная интерпретация весьма маловероятна, поскольку несдвинутый в красную сторону контрпарт [OIII] к линиям слабой ионизации, как ожидалось от _внутренней части_ классической NLR, слаб или отсутствует. Этот факт почти неизбежно приводит нас к третьей и четвертой возможности. #### 4.3.3 Классический линейный регрессор НЛР, модифицированный на малых радиусах Тот факт, что мы не обнаруживаем классическую внутреннюю NLR в форме второго, несмещенного в красную сторону излучения [OIII] компонента, указывает на то, что процессы непосредственно модифицируют / нарушают, по крайней мере, внутреннюю NLR; возможно, в форме взаимодействия радио-струи - облако. Однако сильная зависимость смещения скорости эмиссионной линии от ионизационного потенциала, которую мы обнаруживаем (рис. 3), указывает на то, что мы наблюдаем высоко стратифицированную, фотоионизированную среду, а не локальное взаимодействие из-за ударов и локально нарушенных скоростных полей. #### 4.3.4 Облака NLR, захваченные ветром Самым прямолинейным феноменологическим решением является такое, в котором самые облака CLR и NLR следуют замедленному оттоку. Для этого сценария требуется эффективный механизм ускорения, а возможно, эффективный механизм замедления. Одна из возможностей - это прямое ускорение облаков NLR под действием радиационного давления на газ или пыль; другой - присутствие горячего ветра, который включает в себя облака NLR (см. раздел 4.4). Если ветер формирует замедляющий отток, то увлеченные облака CLR/внутреннего NLR будут иметь самые высокие скорости оттока соответственно, которые будут уменьшаться в зависимости от расстояния до ядра и не затронут внешнюю, низкоионизационную часть NLR. Заманов и др. (2002) сообщили о связи смещения синего края [OIII] с широкой линией CIV. Может ли тот же ветер устоять от диска до высокоионизационной BLR [но не затронув основную часть BLR; раздувая перпендикулярно?], а затем к CLR и внутреннему NLR? На этом изображении NLR галактик BLS1, NLS1 и синих выбросов могут быть внутренне сходными, и движение облаков NLR обычно определяется гравитационным потенциалом бугра. Какие регионы линий излучения будут участвовать в оттоке, будет зависеть от эффективности/рабочего расстояния ветра. Он может присутствовать во всех AGN, но обычно оказывает влияние только на CLR (в AGN с синим смещением железных венчательных линий, но спокойными NLR) или выравнивается даже до достижения CLR. ### Механизмы ускорения и дополнения облаков В то время как феноменологически успешным является вопрос о происхождении ветра/оттока, с другой стороны возникает вопрос о механизме включения и стабильности облака против разрушительных нестабильностей (Mathews & Veilleux 1989, Schiano et al. 1995). Мы обсуждаем несколько возможностей по очереди. Ускорение облака с помощью давления излучения, действующего на пылевые зерна. Действие давления излучения на пылевые зерна, встроенные в газовые облака, является эффективным способом ускорения облаков (например, Binette 1998, Dopita et al. 2002, Fabian et al. 2006). В случае с голубыми выбросами, этот механизм, вероятно, не работает, поскольку мы не ожидаем наличия пыли в высокоионизационной границе линейной области вещества (мы предполагаем здесь, что высокоионизационная часть границы линейной области участвует в оттоке, мотивируясь результатами работы Zamanov et al. (2002), описанной в разделе 4.3.4). В CLR могут присутствовать некоторые пыли (даже небольшая примесь пыли все равно приводит к эффективному излучательному ускорению и обычно все еще прогнозируют достаточно сильные газофазные железные линии; Binette 1998). Визуально наблюдаемые пылеобразные NLR могут присутствовать в отдельных голубых выбросах (например, RXJ0135\(-\)0043), однако большинство из них имеют очень голубую оптическую непрерывность, что говорит против присутствия избытка пылинок вдоль луча наблюдения. Эти аргументы делают сценарий ускорения облаков с помощью давления излучения на пылевые зерна маловероятным. Облачное энтропийное проявление в коллимированных радиоплазменных потоках Известно, что исходящий радиоплазменный поток в виде струй присутствует и охватывает большие расстояния от ядра активной галактической ядра, поэтому он вероятно сказывается на нескольких областях излучения линий на своем пути. Явление облачного энтропия проявление в радиоплазме наблюдалось и изучалось непосредственно в областях звездообразования (Острикер и др., 2001; Стойимирович и др., 2006). Взаимодействие струи с облаком может привести к различным явлениям, включая энтропия облака, отклонение и распад струи, а также разрушение облака (например, Сакстон и др., 2005; Краузе, 2007 и ссылки на них). Здесь интерес представляет энтропия (Бландфорд и Кёнингл, 1979; Шиано и др., 1995; Федоренко и др., 1996). Одной из ключевых проблем является устойчивость облака в отношении различных нестабильностей. Федоренко и др. (1996) предложили концепцию магнитного окова НЛР, которая может позволить энтропии облака в радиоструях. Независимо от теоретических соображений, возникает вопрос о том, обладают ли все синие выбросы нашей выборки мощными радио-джетами. Очень мало известно о радио-свойствах галактик NLS1. В среднем они обычно менее радио-громкие, чем галактики BLS1 (Zhou et al. 2006, Komossa et al. 2006), и имеют некоторые сходства с источниками радиового излучения компактного крутого спектра (Komossa et al. 2006). Четыре из синих выбросов нашей выборки имеют обнаружения радио с помощью FIRST. Они обозначают радиомощность \(P_{\rm 1.4}\)= 10\({}^{22}\)–8 10\({}^{23}\) W Hz\({}^{-1}\) (Табл. 1) при 1.4 ГГц, что сходно с теми АГН, которые Нельсон и Уиттл (1996) отмечают как отклоняющиеся от соотношения \(M_{\rm BH}-\sigma_{*}\). У нас нет информации о радио-морфологии синих выбросов. Источники безразмерные в FIRST за исключением одного замечательного случая: радиоизлучение RXJ0135\(-\)0043 распространяется на расстояние около 10 кпк (или дважды; см. Приложение). Необходимо провести пространственно-разрешенные радионаблюдения источников для поиска наличия джетов и более детального изучения радио-свойств. Варианты моделей термального ветра изучались с целью объяснения кинематики ионизированных поглотителей (Chelouche & Netzer 2005) и NLR. Изотермические модели ветра Паркера Эверетта и Мюррея (2007), изначально рассчитанные для моделирования пространственно разрешенных градиентов скорости NLR NGC 4151 (Das et al. 2005), в целом имели бы правильные свойства для объяснения наших средних выделяющихся синих скоростей сдвига и радиальных изменений скорости. Диапазон значений плотности облаков NLR привел бы к распространению скоростей облаков (см. уравнение (10) Эверетта и Мюррея 2007), тем самым, возможно, объясняя наблюдаемое расширение линии. Однако, как показали также Эверетт и Мюррей (2007), реалистические модели, включающие фотоионизационное нагревание, имеют градиенты температуры, и адиабатическое охлаждение слишком быстро замедляет ветра. Для поддержания изотермичности ветра требуется дополнительный нагрев источника неизвестной природы. Модели Даса и др. (2007), основанные на радиационном ускорении облаков NLR, предполагали, что облака NLR не замедляются достаточно быстро для объяснения градиентов скорости NLR NGC 1068, наблюдаемых с помощью HST; модели работают после введения сил сопротивления от окружающей среды. Детальное моделирование данных, представленных в настоящей статье, вероятно, включало бы несколько из приведенных выше компонентов модели. Однако такое моделирование выходит за рамки данной работы. Высокие соотношения Эддингтона и эффекты ориентацииОбщим для синих выбросов является их высокое соотношение Эддингтона. Может ли высокое \(L/L_{\rm Edd}\) быть механизмом привода ветров? Однако для объяснения того, почему не все ЯАС с высоким \(L/L_{\rm Edd}\) являются синими выбросами, все еще требуются дополнительные эффекты ориентации (как обсуждалось также Марциани и др., 2003, Боросон 2005). Более положенное к горизонту расположение позволило бы нам лучше рассмотреть поток в синих выбросах, тем самым усиливая стратификацию, расширение и эффект сдвига в синюю область. ### Ссылки с (компактными) радиоисточниками и слияния Интересно отметить сходства между явлением синих выдающихся объектов в галактиках NLS1 и в радио-галактиках (см. также Holt et al. 2006). Несколько радио-галактик показывают подобное явление высоких смещений ядерной [OIII] линии к синему цвету и широкой линии (например, Tadhunter et al. 2001, Marziani et al. 2003, Holt et al. 2006, Stockton et al. 2007; см. также Gupta et al. 2005 для связанного явления в УФ). Взаимодействие струи с облаками в (внутреннем) NLR является предпочтительной интерпретацией для большинства этих источников. Эти объекты могут представлять ранние стадии эволюции радио-источников (Tadhunter et al. 2001). Радио-галактики с синими выдающимися объектами в [OIII] обычно являются компактными источниками с плоским спектром, поглощаются и яркие в инфракрасном диапазоне. У некоторых (например, PKS1549\(-\)79 and PKS0736+01) есть доказательства того, что мы имеем почти прямой вид (Tadhunter et al. 2001, Marziani et al. 2003). Как указано ранее, сильная стратификация, которую мы видим в синих выдающихся объектах NLS1, говорит против локальных взаимодействий струи с облаками в тех галактиках, но согласуется с облаками NLR, втянутыми в выбрасывающуюся радио-плазму. Синие выбросы среди радиогалактик свидетельствуют о недавних слияниях. Что касается общих сведений о галактиках NLS1, нет доказательств того, что большинство из них подверглись недавним слияниям или обладают избытком спутниковых галактик (Krongold et al., 2001, Ryan et al., 2007). О малоизвестных галактиках-хостах нашей выборки синих выбросов известно очень мало. Однако IRAS11598-0112 действительно представляет собой слияние с ярко выраженными приливными хвостами (Veilleux et al., 2002), являющимися ультраяркими в инфракрасном диапазоне. Изучение изображений SDSS других галактик нашей выборки не демонстрирует ярко нарушенные изображения галактик, указывающие на текущие слияния, но это требует подтверждения более глубокими изображениями. Одна галактика, RXJ0135-0043, демонстрирует признаки отцентрированного ядра. Этот эффект может быть вызван взаимодействием, быть имитированным пылью или иметь другое происхождение. ### Отдача черных дыр? Недавние симуляции слияния черных дыр предсказывают скорости отдачи черных дыр из-за излучения гравитационных волн, достигающие нескольких тысяч км/c (например, Campanelli et al. 2007; обзор Pretorius 2007). Возможно, высокие относительные скорости выхода из областей испускания AGN по отношению к галактике-хозяйке могут возникнуть, если отталкивающаяся черная дыра сохраняет свою область излучения BLR и внутреннюю область NLR (Bonning et al. 2007). Применительно к голубым выбросам, если бы они содержали отталкивающиеся BH, их вся область BLR (а также высокоионизационная область NLR) должна была бы показывать высокие синие сдвиги, в то время как "остаточная" NLR все еще должна была бы проявляться в линиях низкой ионизации. В таком случае, мы ожидаем, что широкая составляющая линий Бальмера будет иметь наибольшие синие сдвиги среди всех линий испускания, однако это не наблюдается. Сдвиги в широкой H\(\beta\) меньше, чем в [OIII]. ### Дальнейшая работа База данных SDSS хорошо подходит для систематического поиска более голубых выбросов. Чжоу и др. (2006) упоминают в обходе о наличии нескольких экстремальных среди своей выборки галактик NLS1, но не обсуждают их более подробно. Пространственно-распределенная оптическая спектроскопия позволит нам непосредственно измерять ширину линий, скорости оттока и т.д. в зависимости от расстояния до ядра⁵. Спектроскопия в ИК и УФ диапазонах покажет, сохраняются ли тенденции (корреляция с ионизационным потенциалом) в ИК коронных линиях и высокоионизационных УФ широких линиях. Рентгеновские измерения голубых выбросов будут полезны для поиска признаков высокоскоростных ионизированных оттоков и для определения, выделяются ли голубые выбросы в пространстве корреляции АГН при добавлении их рентгеновских свойств (крутизна рентгеновского спектра, изменчивость) к анализу корреляций. (Высокоразрешающие) радионаблюдения всех галактик позволят провести дальнейшее сравнение голубых выбросов в радиогалактиках и галактиках NLS1 и установить, присутствуют ли радиолучи в голубых выбросах NLS1. Радионаблюдения имеют потенциал подтвердить гипотезу о полюсном расположении голубых выбросов, если будет обнаружено релятивистское направленное излучение. Изображения с помощью HST позволят определить, есть ли признаки недавних слияний в галактиках-хозяевах голубых выбросов. В частности, симуляции слияния галактик прогнозируют сильные оттоки в финальной фазе слияния (например, Спрингел и др. 2005). Изображения позволят нам проверить, находятся ли голубые выбросы в такой фазе. [FOOTNOTE:5][ENDFOOTNOTE] (Примечание 5) Если прямолинейная интерпретация синих аномалий верна, они также являются полезными тестовыми стендами для вопроса, связанного с тем, насколько ширина широкой линии H\(\beta\) систематически зависит от ориентации. Увеличение размера выборки позволит нам более строго проверить, имеет ли широкая компонента H\(\beta\) систематически меньшую ширину у синих аномалий. Если это так, это бы означало, что облака BLR расположены в плоскости, и мы систематически недооцениваем массы ЧДР в этих объектах, а также, возможно, в галактиках NLS1 в целом. Если, напротив, их BLR сферическая, мы бы не наблюдали систематически узкую линию H\(\beta\) в объектах, видимых с прямолинейной ориентацией, и не стали бы беспокоиться о правильности оценок масс ЧДР. Наши предварительные результаты указывают на то, что последнее является верным. На теоретической стороне возникает вопрос о том, какие ветры могут действовать на большие расстояния, охватывающие область высокой ионизации BLR, CLR и существенную часть NLR, прогнозировать наблюдаемый градиент в скорости облаков (\(\sim\)1000 км с\(^{-1}\) для облаков с высокой ионизацией эмиссионной линии близко к ядру и несколько сотен км с\(^{-1}\) дальше на типичных масштабах NLR, в то время как внешняя NLR в основном не повреждается) и обеспечивать долговечность эмиссионных линий облаков. ## 5. Резюме и заключение При аномально высоком смещении скорости в синем [OIII] линия выделения проявляются сильнее или полностью доминируют вторичные влияния на кинематику NLR. Изучение таких объектов имеет большое значение для (1) анализа полезности и ограничений ширины [OIII] как прокси для дисперсии скорости звезд; (2) понимания происхождения и динамики NLR; (3) исследования механизмов управления выбросами AGN на больших масштабах; и (4) исследования возможных связей с результатами симуляций слияний, которые предсказывают, что значительная доля ISM слияния должна быть выброшена. Мы систематически изучили оптические свойства таких AGN с высоким смещением в синем [OIII], отклоняющихся от соотношения \(M_{\rm BH}-\sigma_{\rm[OIII]}\) для галактик BLS1 и NLS1, и получили следующие результаты: \(\bullet\) Все они имеют высокие отношения Эддингтона (\(L/L_{\rm{edd}}\)=0.5–1.5) и узкие бальмеровские линии БЛР (FWHM(H\(\beta_{\rm b}\))=1200–1800 км с\({}^{-1}\)), что делает их галактиками NLS1. Доля синих выбросов среди нашей выборки NLS1 составляет 16% (\(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}150\) км с\({}^{-1}\)), и 5% при наивысших скоростях выталкивания (\(v_{\rm[OIII]}\mathrel{\hbox{\hbox to 0.0pt{\lower 2.365pt\hbox{$\sim$}} \kern-3.0pt\raise 1.72pt\hbox{$>$}}}250\) км с\({}^{-1}\)). Хотя синие выбросы действительно усиливают корреляции, которые наблюдаются среди всей популяции BLS1-NLS1, мы не обнаруживаем сильных корреляций скорости выталкивания [OIII] с отношением Эддингтона внутри этой самой группы синих выбросов; возможно, из-за малого размера выборки. \(\bullet\) Мы обнаруживаем сильную корреляцию между смещением линии испускания и ионизационным потенциалом, и подтверждаем сильную корреляцию между смещением [OIII] и шириной линии [OIII]. Присутствие классического камеры неактивного АВП "внешнего" обозначается существованием низкоионизационных линий, ширинами линий [SII], которые помещают синие выбросы на той же связи \(M_{\rm BH}-\sigma_{\rm[SII]}\) , что и другие галактики тира BLS1 и NLS1, и по средним плотностям АВП, похожим на другие галактики NLS1. С другой стороны, ожидаемая нулевая синева [OIII] испускания из неактивного АВП "внутреннего" слабая или отсутствует. \(\bullet\) Все эти наблюдения вместе ставят жесткие ограничения на модели: Мы отдаем предпочтение сценарию, в котором облака NLR голубых выбросов захватываются в замедляющийся ветер. Похожие, менее мощные ветры могут присутствовать у всех AGN, но обычно они затрагивают только CLR (в AGN с синеватыми железными корональными линиями, но спокойными NLR), либо они останавливаются еще до достижения CLR, затрагивая только высокоионизационную BLR. \(\bullet\) Механизм, который приводит к ускорению и замедлению ветра, на данный момент является предметом спекуляций, но может быть связан с высокими значениями отношений Эддингтона галактик. Дополнительные ориентационные эффекты (близкие к полюсу взгляды), ранее рассматриваемые для объяснения корреляции смещения [OIII] к синей стороне с шириной линии синих выбросов, также могут объяснить обнаруженную нами сильную ионизационную стратификацию. \(\bullet\) Два голубых аномальных значения имеют независимые измерения массы BH / скорости рассеяния звезд и находятся на или близко к соотношению \(M_{\rm BH}-\sigma\) неактивных галактик. Это, вместе с тем, что ширина широкой H\(\beta\) не коррелирует с [OIII] скорости истечения, указывает на то, что если голубые аномалии действительно видны более к нас, это обстоятельство не сильно отражается на ширине их H\(\beta\), что говорит о том, что геометрия их BLR ближе к сферической, чем к плоской. \(\bullet\) Самым замечательным из синих аномалий является галактика RXJ01354\(-\)0043. В отличие от других галактик NLS1, ее радиоизлучение распространено и, возможно, двойное, оптические линии Бальмера в ней имеют двенадцать пиков, а оптический спектр демонстрирует сильные поглощающие линии от галактики-хозяина. Связь между синими аномалиями в галактиках NLS1 и (компактными) радиогалактиками требует дальнейшего исследования. ## 6. Приложение: Примечания по отдельным объектам В SDSS-NLS1 образцах Уильямса и др. (2002) и Андерсона и др. (2003) включены несколько источников. Высокие сдвиги в синюю область спектра [OIII] для SDSSJ115533.50+010730.4 и RXJ01354\(-\)0043 были описаны Биан и др. (2005). Боросон (2005) измерил сдвиги в синюю область спектра [OIII] для NGC450#86, RXJ01354\(-\)0043, PG1244+026 и SDSS17184+5734. Здесь мы предоставляем краткое описание многоволновых свойств синих выбросов, собранных из литературы, и даем комментарии на основе нашего оптического спектрального анализа. Галактики указаны в порядке убывания сдвига [OIII] в синюю область спектра. SBS0919+515 Этот АГН известен как источник рентгеновского излучения, впервые обнаруженный с помощью обсерватории Эйнштейна (Чанан и др., 1981), большую часть исследований которого проведено в рентгеновском диапазоне (например, Боллер и др., 1996, Воэн и др., 2001), и оптически был определен как галактика NLS1 Стивенсом (1989). Он показывает наивысший сдвиг в сторону синего конца спектра [OIII] из нашей выборки (\(v_{\rm[OIII]}=430\) км с\({}^{-1}\)). SDSSJ115533.50+010730.4Этот АГН был обнаружен в рентгеновском диапазоне во время обзора всего неба ROSAT (Voges et al. 1999) и впервые был классифицирован как галактика NLS1 Уильямсом и др. (2002). Он имеет второй по величине сдвиг скорости [OIII] в нашей выборке (\(v_{\rm[OIII]}=330\) км с\({}^{-1}\)), сильно синеватую [NeV] и слабую эмиссию корональных линий [FeX] со сдвигом в синюю сторону, соответствующим \(v_{\rm[FeX]}\approx 1000\) км с\({}^{-1}\), одни из самых больших сдвигов в синюю сторону, когда-либо сообщенные для корональных линий. RXJ01354\(-\)0043 (SDSSJ013521.68\(-\)004402.2) Этот АГН был обнаружен в рентгеновском и радио диапазоне (Brinkmann et al. 2000, Wadadekar 2004) и был оптически идентифицирован как галактика NLS1 авторами Williams et al. (2002). Он отличается несколькими особенностями. Мы обнаружили, что его оптический спектр, по-видимому, контролируется галактикой-хозяином. Обнаружены сильные поглощающие линии из высших балмеровских линий, Ca H&K и NaID (Рис. 5). Оптическое непрерывное излучение АГН либо является внутренне слабым, либо поглощено (что требовало бы особого геометрии поглотителя, учитывая наличие широких балмеровских линий). RXJ01354\(-\)0043 обнаружен с помощью GALEX⁶ и имеет красные ультрафиолетовые цвета. У его узких балмеровских линий двойной пик, с разделением порядка \(\sim\)580 км с\({}^{-1}\), или они подвержены остаточным, исключительно сильным и красносдвинутым, особенностям галактики-хозяина, что маловероятно, учитывая силу H\(\alpha\). Разложение линий, показанное на Рис. 5, предполагает одинаковую ширину узкого ядра H\(\beta\) и двух линий [NII], фиксированную ширину [SII] и также предполагает фиксированное отношение линий [NII]. Оставшийся профиль моделировался с помощью двух гауссовых кривых с свободными параметрами и может быть хорошо аппроксимирован широким компонентом плюс вторым, красносдвинутым относительно узким компонентом. RXJ01354\(-\)0043 был обнаружен с помощью FIRST с радио потоком 2 милиджи и есть доказательства наличия расширенного радиоизлучения (Becker et al. 1997⁷), соответствующего масштабу порядка \(\sim\)10 кпк. Это необычно, потому что известно немного NLS1 галактик с широко распространенным радиоизлучением (Ulvestad et al 1995, Komossa et al. 2006, Yuan et al. 2008). Изучая вырез изображения FIRST, источник кажется двойным. Среди линий излучения только балмеровские линии оказываются двойными по пикам. RXJ01354\(-\)0043 - первый синий выброс, показывающий это явление. Объяснения включают взаимодействие клуба и облака, биполярный отток или, за пределами, наблюдаемая сильная балмеровская поглощающая линия (что редко встречается из-за недостаточной оселенности уровня; Hall 2007, Lu et al. in prep.). Мы использовали поглощающие линии звезд от галактики-хозяина для измерения \(\sigma_{*}\). Мы получаем \(\sigma_{*}=82\) км с\({}^{-1}\), что хорошо согласуется с измерением на основе [SII], \(\sigma_{\rm[SII]}=106\) км с\({}^{-1}\), и располагает RXJ01354\(-\)0043 (практически идеально) на связи \(M_{\rm BH}-\sigma_{*}\) неактивных галактик (Рис. 1). [FOOTNOTE:6][ENDFOOTNOTE] [ССЫЛКА_В_СНОСКЕ:6][КОНЕЦ_ССЫЛКИ_В_СНОСКЕ:6] [ОПИСАНИЕ:7][КОНЕЦ ОПИСАНИЯ] NGC450#86 Идентифицирована как галактика NLS1 Уильямсом и др. (2002) и обнаружена в рентгеновском диапазоне в ходе всескайского обследования ROSAT (Вогес и др. 1999). SDSSJ032606.75+011429.9A - в основном неизвестная галактика с оптическим спектром NLS1 (Уильямс и др., 2002). Отсутствие обнаружения радио или рентгеновского излучения было сообщено. IRAS 11598\(-\)0112 Эта галактика является сверхсветимой в инфракрасном диапазоне (Murphy et al. 1996, Kim & Sanders 1998) с одним ядром и заметными приливными хвостами (Veilleux et al. 2002). Ее оптический спектр соответствует спектру галактики NLS1 (Moran et al. 1996). Она почти радиоактивна с 1,4 ГГц радиоиндексом \(R\approx 5\) (Komossa et al. 2006) и была впервые обнаружена в рентгеновском диапазоне с помощью ROSAT (Voges et al. 1999). Излучение FeII в ее оптическом спектре не хорошо описывается нашим шаблоном FeII. В частности, "красные" и "синие" комплексы FeII не совпадают хорошо, и кажется, что красное смещение источника отличается от красного смещения FeII. Сильное излучение неизвестной природы остается на более низкой частоте [OIII]. Формально, мы можем описать его с помощью дополнительного компонента [OIII], широкого (FWHM([OIII])=1800 km s\({}^{-1}\)) и сильно синего смещения (\(v\)=1300 km s\({}^{-1}\)). Если это реально, это может представлять собой экстремальное синее крыло, или может указывать на наличие дополнительного вспышек звезд/компонента, вызванного ударом. Структуру нужно подтвердить независимой спектроскопией. Обнаружен с помощью ROSAT (Brinkmann et al. 1999) и оптически идентифицирован как NLS1 Вильямсом и др. (2002). PG1244+026 Этот активный ядро галактики (AGN) (Green et al., 1986) является известным источником рентгеновского, ультрафиолетового, инфракрасного и радиоизлучения (например, Elvis et al., 1986, Kellerman et al., 1989, Sanders et al., 1989, Fiore et al., 1998, Ballantyne et al., 2001, Jimènez-Bailòn et al., 2005) c оптическим спектром NLS1 (Miller et al., 1992, Veron-Cetty et al., 2001). Он слабо излучает в радиодиапазоне с радиоиндексом \(R=0.5\) при 5 ГГц (Kellerman et al., 1989). Хаяшида (2000) и Черни et al. (2001) определили его массу черной дыры на основе изменчивости рентгеновского излучения (спектр плотности мощности). Черни et al. (2001) сообщают, что \(\log M_{\text{{BH}}}=5.9\), что согласуется с нашим значением \(\log M_{\text{{BH}}}=6.2\), полученным с использованием соотношения Каспи et al. (2005). Мы обнаружили в его оптическом спектре излучение [FeX] со скоростью оттока 640 км/с. RXJ09132+3658 Обнаружено в рентгеновском диапазоне с помощью ROSAT (Voges et al. 1999, Brinkmann et al. 2000) и в радиодиапазоне в ходе FIRST-опроса (Becker et al. 1997) и определено как галактика NLS1 Xu et al. (1999). DX признательно признаёт финансовую поддержку Китайского национального фонда науки (NSFC) в рамках гранта NSFC-10503005, а также поддержку от MPG/MPE. HZ выражает благодарность Александру фон Гумбольдту, NSFC (грант NSF-10533050) и программе 973 (No. 2007CB815405) за поддержку. LB признателен гранту CONACyT J-50296. Мы благодарим нашего рецензента за его/ее комментарии и предложения, а также членов новой группы "Физика галактических ядер" института MPE и J. Сулентика, D. Прогу и D. Мерритта за обсуждения. В ходе исследования использовались база данных SDSS и база данных NASA/IPAC экстрагалактических объектов (NED), эксплуатируемая Лабораторией реактивного двигателя Калифорнийского технологического института на основании контракта с Национальным управлением аэронавтики и космонавтики. Финансирование SDSS и SDSS II предоставлено Альфредом П. Слоунским фондом, участвующими учреждениями, Национальным фондом науки, Министерством энергетики США, Национальным управлением аэронавтики и космонавтики, Японской монбукагакусё, Макс-Планк обществом и Советом по финансированию высшего образования Англии. SDSS управляется Консорциумом астрофизических исследований для участвующих учреждений. Участвующие учреждения - Американский музей естествознания, Астрофизический институт Потсдама, Университет Базеля, Университет Кембриджа, Университет Кейс Вестерн Резерв, Университет Чикаго, Университет Дрексель, Ферми-Лаборатория, Институт продвинутых исследований, Группа участия Японии, Университет Джонса Хопкинса, Совместный институт ядерной астрофизики, Институт Кавли по астрофизике частиц и космологии, Корейская научная группа, Китайская академия наук (LAMOST), Лос-Аламосская национальная лаборатория, Макс-Планк институт астрономии (MPIA), Макс-Планк институт астрофизики (MPA), Университет Нью-Мексико, Университет Огайо, Университет Питтсбурга, Университет Портсмута, Принстонский университет, Юридическое обсерваторное управление США и Университет Вашингтона. ## Ссылки * (Abazajian et al. 05) Abazajian, K., и др. 2005, AJ, 129, 1755 * (Anderson et al) Anderson, S.F., и др. 2003, AJ, 126, 2209 * (Aoki et al. 2006) Aoki, K., Kawaguchi, T., & Ohta, K. 2005, ApJ, 618, 601 * (Ballantyne et al. 2001) Ballantyne, D.R., Iwasawa, K., & Fabian, A.C. 2001, MNRAS, 323, 506 * (Barth et al. 05) Barth, A.J., Greene, J.E., & Ho, L.C. 2005, ApJ, 619, L151 * (Becker et al. 1997) Becker, R.H., Helfand, D.J., White, R.L., Gregg, M.D., & Laurent-Muehleisen, S.A. 1997, ApJ, 475, 479 * (Bennert et al. 2006) Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006, A&A, 456, 953 * (Bian et al.) Bian, W., & Zhao, Y. 2004, MNRAS, 347, 607 * (Bian et al.) Bian, W., Yuan, Q., & Zhao, Y. 2005, MNRAS, 364, 187 * (Binette 1998) Binette, L. 1998, MNRAS, 294, L47 * (Binette et al. 1997) Binette, L., Wilson, A.S., Raga, A., Storchi-Bergmann, T., 1997, A&A, 327, 909 * (Blandford and Kenigl 1979) Blandford, R., & Königl, A. 1979, ApL, 20, 15 * (Boller et al. 1996) Boller, T., Brandt, W.N., & Fink, H., 1996, A&A, 305, 53 * (Bonning et al. 2007) Bonning, E.W., Shields, G.A., & Salviander, S. 2007, ApJ, 666, L13 * (Boroson 2002) Boroson, T.A. 2002, ApJ, 565, 78 * (Boroson 2003) Boroson, T.A. 2003, ApJ, 585, 647 * (Boroson 2005) Boroson, T.A. 2005, ApJ, 130, 381 * (Botte et al. 04) Botte, V., Ciroi, S., Rafanelli, P., & Di Mille, F. 2004, AJ, 127, 3168 * (Botte et al. 05) Botte, V., Ciroi, S., Di Mille, F., Rafanelli, P., & Romano, A., 2005, MNRAS, 356, 789 * (Brinkmann et al. 1999) Brinkmann, W., и др. 1999, A&AS, 134, 221 * (Brinkmann et al. 2000) Brinkmann, W., и др. 2000, A&A, 356, 445 * (Campanelli et al. 2007) Campanelli, M., Lousto, C.O., Zlochower, Y., & Merritt, D. 2007, PhRvL, 98, 1102 * (Cecil et al. 2002) Cecil, G., и др. 2002, ApJ, 585, 627 * (Chanan et al..., MNRAS, 242, 721 * (Tremaine et al. 2002) Tremaine, S., и др. 2002, ApJ, 574, 740 * (Ulvestadt et al. 1995) Ulvestad, J.S., Antonucci, R.R.J., & Goodrich, R.W. 1995, AJ, 109, 81 * (Vaughan et al. 2001) Vaughan, S., Edelson, R., Warwick, R.S., Malkan, M.A., & Goad, M.R. 2001, MNRAS, 327, 673 * (Veilleux 1991) Veilleux, S. 1991, ApJ, 369, 331 * (Veilleux et al. 2002) Veilleux, S., Kim, D.-C., & Sanders, D.B. 2002, ApJS, 143, 315 * (Veilleux et al. 2005) Veilleux, S., Cecil G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 * (Veron 1981) Véron, M.P. 1981, A&A, 100, 12 * (Veron-Cetty et al.)Véron-Cetty, M.P., Véron, P., & Goncalves, A.C. 2001, A&A, 372, 730 * (Veron-catalogue 2003) Véron-Cetty, M.P., & Véron, P. 2003, A&A, 412, 399 * (Veron-Cetty et al.) Véron-Cetty, M.P., Joly, M., & Véron, P. 2004, A&A, 417, 515 * (Voges et al. 1999) Voges, W., и др. 1999, A&A, 349, 389 * (Wadadekar 2004) Wadadekar, Y. 2004, A&A, 416, 35 * (Wandel 2002) Wandel, A. 2002, ApJ, 565, 762 * (Wang and Lu 01) Wang T., & Lu Y. 2001, A&A, 377, 52 * (Watson et al.07) Watson L., Mathur S., & Grupe D. 2007, AJ, 133, 2435 * (Whittle 1992) Whittle, M. 1992, ApJ, 387, 109 * (Williams et al) Williams, R.J., Pogge, R.W., & Mathur, S. 2002, AJ, 124, 3042 * (Wyithe and Loeb 2003) Wyithe, J.S.B., & Loeb. A. 2003, ApJ, 595, 614 * (Xu et al. 1999) Xu, D., Wei, J.Y., & Hu, J.Y. 1999, ApJ, 517, 622 * (Xu et al. 2007a) Xu, D., Komossa, S., Zhou, H., Wang, T., & Wei, J. 2007, ApJ, 670, 60 * (Xu et al. 2008) Xu, D., и др. 2008, AJ, to be submitted * (Young et al. 2007) Young, S., Axon, D.J., Robinson, A., Hough, J.H., & Smith, J.E. 2007, Nat, 450, 74 * (Yuan et al. 2008) Yuan, W., и др. 2008, ApJ, submitted * (Zamanov et al. 2004) Zamanov, R., и др. 2002, ApJ, 576, L9 * (Zhou et al. 06) Zhou, H.-Y., и др. 2006, ApJS, 166, 128 [TABLE:S6.T1][ENDTABLE] [FIGURE:S6.F1][ENDFIGURE] [ФИГУРА:S6.F2][КОНЕЦФИГУРЫ] [FIGURE:S6.F3][ENDFIGURE] (Ошибка: неверный формат ввода. Пожалуйста, укажите правильный формат.) [FIGURE:S6.F4][ENDFIGURE] [FIGURE:S6.F5][ENDFIGURE] - [РИСУНОК:S6.F5][КОНЕЦ РИСУНКА] Переведите контекст из английского на русский. Сохраните форматирование уравнений.

# New analytic models of ”traversable”  wormholes ###### Abstract The analytic solution of the general relativity equations for spherically symmetric wormholes are given. We investigate the special case of a ”traversable”  wormhole i.e., one allowing the signal to pass through it. The energy-momentum tensor of wormhole matter is represented as a superposition of a spherically symmetric magnetic field and dust matter with negative matter density. The dynamics of the model are investigated. We discuss both the solution of the equation with a \(\Lambda\)-term and without it. Superposing enough dust matter, a magnetic field, and a \(\Lambda\)-term can produce a static solution, which turns out to be a spherical Multiverse model with an infinite number of wormholes connected spherical universes. Corresponding solution can be static and dynamic. Alexander Shatskiy\({}^{1}\), I.D. Novikov\({}^{1,2,3}\), N.S. Kardashev\({}^{1}\) \({}^{1}\)Astro Space Center, Lebedev Physical Institute, Moscow, Russia, [email protected] \({}^{2}\)Niels Bohr Institute, Blegdamsvej 17, DK-2100 Copenhagen, Denmark \({}^{3}\)Kurchatov Institute, Moscow, Russia ## 1 Introduction A wormhole (WH) [1]-[19]) is a hypothetical object described by a nonsingular solution of the Einstein equations with two large (or infinite) space-time regions connected by a throat. The two large space-time regions can be located in one universe or belong to different universes in the Multiverse model (see [18]). In the last case, ”traversable”  WHs afford a unique opportunity to explore other universes. In the present paper, we analytically study the dynamics of a spherical model of a non-equilibrium WH filled with matter. This matter consists of a magnetic field and dust with negative mass density. The obtained solution therefore generalizes the Tolman solution [20] for a model with a spherically symmetric electromagnetic field. As we see below, this generalization leads to essentially new and important solutions. We use the method of calculations of physical quantities in the frame comoving with dust. As the initial model for a WH, we use a static model in which gravitational accelerations are everywhere identically zero. Hence, the effective masses of both WH mouths vanish, although the geometry of three-dimensional space is certainly non-Euclidean. Such a model is considered in [19] and [17], where all matter is represented by a gravitating scalar field. We change the scalar field into a superposition of an electro- magnetic field and dust matter with negative energy density, which turns out to be a methodologically important development and generalization of these models. This allows us to apply methods of Tolman’s problem to calculate the model (see [20], [21], [22]); these methods were generalized and further developed by Shatskiy (see [23] and [24]). To further generalize and develop this method, we introduce the cosmological \(\Lambda\)-term into the model. This allows obtaining a principally new solution (see Section 6) for a static spherical model of the Multiverse. This model includes a infinite number of spherical worlds connected by throats. To our knowledge, this is the first analytic model of this type. In the obtained solution, the Multiverse can have its total energy density positive everywhere in space. In addition, this solution can be generalized by the same method to the case of a dynamic model shifted from equilibrium by an excess (or shortage) of dust or by the \(\Lambda\)-term. Some methodological details see in [25] ## 2 Einstein equations We use the Armendariz-Picon static spherically symmetric solution of the Einstein equations [17] for the description of the unperturb WH model¹: [FOOTNOTE:1][ENDFOOTNOTE] \[ds^{2}=dt^{2}-dR^{2}-r^{2}(d\theta^{2}+\sin^{2}\theta\,d\varphi^{2})\,,\quad r ^{2}(R)=q^{2}+R^{2}\,.\] (1) The minimum allowed radius of this WH is \({r_{{}_{0}}=q}\) (the radius of the throat²). [FOOTNOTE:2][ENDFOOTNOTE] Usually, this solution is related to the energy-momentum tensor of a scalar field (see [19], [17]). In the present paper, we suggest another interpretation of this solution related to a different representation of the energy-momentum tensor. This new interpretation of solution (1) can correspond to the energy-momentum tensor represented as \[T^{n}_{k}=\left(\begin{tabular}[]{c c c c}$-\frac{q^{2}}{8\pi r^{4}}$&0&0&0\\ 0&$+\frac{q^{2}}{8\pi r^{4}}$&0&0\\ 0&0&$-\frac{q^{2}}{8\pi r^{4}}$&0\\ 0&0&0&$-\frac{q^{2}}{8\pi r^{4}}$\\ \end{tabular}\right)=\left(\begin{tabular}[]{c c c c}$+\frac{q^{2}}{8\pi r^{4} }$&0&0&0\\ 0&$+\frac{q^{2}}{8\pi r^{4}}$&0&0\\ 0&0&$-\frac{q^{2}}{8\pi r^{4}}$&0\\ 0&0&0&$-\frac{q^{2}}{8\pi r^{4}}$\\ \end{tabular}\right)+\left(\begin{tabular}[]{c c c c}$-\frac{q^{2}}{4\pi r^{4} }$&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{tabular}\right)\] (2) The first term in the right-hand side corresponds to the energy-momentum tensor of a static magnetic field with the effective magnetic charge \(q\) and the second term describes dust matter with the negative energy density \[\varepsilon_{d}=-\frac{q^{2}}{4\pi r^{4}}\] (3) This possible representation of the tensor \({T^{n}_{k}}\) is different from its equivalent representation as the energy-momentum tensor of a scalar field adopted in previous papers [17]-[28]. An excess (or shortage) of dust (relative to \({\varepsilon_{d}}\)) is not in equilibrium and initiates motion. Because dust layers are relatively independent, it is possible to integrate the equations of motion for dust in a way similar to the solution of Tolman’s problem [20]. In essence, it is the same as Tolman’s problem in a centrally symmetric and static electric (or magnetic) field for uncharged dust. We seek the metric tensor of the solution in the form³: [FOOTNOTE:3][ENDFOOTNOTE] \[ds^{2}=dt^{2}-e^{\lambda}dR^{2}-r^{2}(d\theta^{2}+\sin^{2}\theta\,d\varphi^{2}),\] (4) where \(r^{2}\) and \(e^{\lambda}\) are functions of both \(R\) and \(t\). Below, we justify this choice of the metric. We consider the problem in the presence of a \(\Lambda\)-term. The Einstein equations corresponding to metric (4) can be written as⁴: [FOOTNOTE:4][ENDFOOTNOTE] \[8\pi T_{t}^{t}=8\pi\varepsilon+q^{2}/r^{4}+\Lambda=-e^{-\lambda} \left(2rr_{,_{RR}}+r^{2}_{,_{R}}-rr_{,_{R}}\lambda_{,_{R}}\right)/r^{2}+\left( rr_{,_{t}}\lambda_{,_{t}}+r^{2}_{,_{t}}\right)/r^{2}+1/r^{2}\,,\] (5) \[8\pi T_{R}^{R}=q^{2}/r^{4}+\Lambda=\left(2rr_{,_{tt}}+r^{2}_{,_{ t}}\right)/r^{2}-e^{-\lambda}r^{2}_{,_{R}}/r^{2}+1/r^{2}\,,\] (6) \[8\pi T^{R}_{t}=0=e^{-\lambda}\left(2r_{,_{Rt}}-r_{,_{R}}\lambda_ {,_{t}}\right)/r\,,\] (7) \[8\pi T^{\theta}_{\theta}=8\pi T^{\varphi}_{\varphi}=-q^{2}/r^{4} +\Lambda=-\left\{e^{-\lambda}\left[2r_{,_{RR}}-r_{,_{R}}\lambda_{,_{R}}\right] -2r_{,_{tt}}-r\lambda_{,_{tt}}-r\lambda_{,_{t}}^{2}/2-r_{,_{t}}\lambda_{,_{t}} \right\}/(2r)\,.\] (8) **Thus, the energy-momentum tensor includes three types of matter: a centrally symmetric magnetic field, a cosmological \(\Lambda\)-term, and dust matter with the density⁵\(\varepsilon\).** [FOOTNOTE:5][ENDFOOTNOTE] ## 3 Solution and the Initial Conditions Equation (7) can be integrated with respect to time: \[e^{-\lambda}r^{2}_{,_{R}}=F_{1}(R)\,.\] (9) At the throat, the condition \({r_{,_{R}}=0}\) must be satisfied, and therefore \[F_{1}(0)=0\,.\] (10) By substituting (9) in Eqn (6), we obtain \[\frac{q^{2}}{r^{2}}+\Lambda r^{2}=\left(rr^{2}_{,_{t}}\right)_{,t}/r_{,_{t}}-F _{1}+1\,.\] (11) Integrating this equation with respect to time yields \[\frac{q^{2}}{r}-\Lambda r^{3}/3+rr^{2}_{,_{t}}+(1-F_{1})r=F_{2}(R)\,.\] (12) The functions \({F_{1}(R)}\) and \({F_{2}(R)}\) determine the initial conditions for the velocity and dust density distributions. With \({\lambda_{,_{t}}}\) and \({\lambda_{,_{tt}}}\) expressed from Eqn (7), Eqn (8) can be rewritten as \[\left[q^{2}/r^{2}+\Lambda r^{2}+e^{-\lambda}r_{,_{R}}^{2}-r_{,_{t}}^{2}-2rr_{, _{tt}}\right]_{,_{R}}=0\,.\] (13) When Eqn (6) is satisfied, integrating Eqn (13) yields an identity. **This identity is the consequence of setting the time component of metric (4) to unity, which justifies this choice of the metric.** It is worth noting from the methodological standpoint that this form of the metric for dust is obvious because dust is pressureless and hence the comoving frame is simultaneously a synchronous one. But this is not so obvious when a spherically symmetric electromagnetic field is added, and the obtained identity is a consequence of the absence of interaction between uncharged dust and the electromagnetic field. Moreover, the Lorentz transformation along the magnetic field lines does not change this field, which justifies the use of the dust comoving reference frame. For motion in this frame (along the field), the electromagnetic field remains invariant. If the metric could not be represented in form (4), further calculations would be impossible. It is this non-obvious fact that allowed us to successfully develop our method and to obtain all important results. Multiplying Eqn (5) by \({r^{2}r_{,_{R}}}\) and expressing \({\lambda_{,_{t}}}\) from Eqn (7), we obtain \[8\pi\varepsilon r^{2}r_{,_{R}}+\left[\Lambda r^{3}/3-q^{2}/r-r(1-F_{1})-rr_{,_ {t}}^{2}\right]_{,_{R}}=0\,.\] (14) Integrating this with respect to \(R\) from \(0\) to \(R\) with account for (10) yields \[\int\limits_{0}^{R}8\pi\varepsilon r^{2}r_{,_{R}}\,dR-q^{2}/r+\Lambda r^{3}/3- r(1-F_{1})-rr_{,_{t}}^{2}=-q^{2}/r_{{}_{0}}+\Lambda r_{{}_{0}}^{3}/3-r_{{}_{0} }-r_{{}_{0}}r_{{}_{0},_{t}}^{2}\,.\] (15) Here, we took into account that the function \({r(R=0)=r_{{}_{0}}(t)}\) can be time-dependent. Expressing \({rr_{,_{t}}^{2}}\) from (12) and substituting it in (15), we obtain \[\int\limits_{0}^{R}8\pi\varepsilon r^{2}r_{,_{R}}\,dR=F_{2}(R)-q^{2}/r_{{}_{0} }-r_{{}_{0}}+\Lambda r_{{}_{0}}^{3}/3-r_{{}_{0}}r_{{}_{0},_{t}}^{2}\,.\] (16) The derivative of this expression with respect to \(R\) yields one more integral of motion (which expresses mass conservation in the comoving volume): \[8\pi\varepsilon r^{2}r_{,_{R}}=\frac{dF_{2}}{dR}\,.\] (17) The Bianchi identities⁶: [FOOTNOTE:6][ENDFOOTNOTE] \[T^{n}_{k;n}=\frac{1}{\sqrt{-g}}\,\frac{\partial(T^{n}_{k}\sqrt{-g})}{\partial x ^{n}}-\frac{T^{nl}}{2}\,\frac{\partial g_{nl}}{\partial x^{k}}=0\] (18) are contained in the Einstein equations, their components \({k=t,\theta,\varphi}\) vanish identically, and the component \({k=R}\) yields the result in (17), which is an analogue of the integral for the pure-dust solution (see [31], \(\lx@sectionsign\)103) in the theory of the evolution of a dust cloud. The explicit form of the function \({e^{\lambda}(R,t)=r_{,_{R}}^{2}/F_{1}}\) and an implicit form of the function \({r^{2}(R,t)}\) are obtained in Section 4. **Below, we use the index ”i”  to denote all quantities at the initial instant \({t=0}\).** The velocity distribution is set to zero initially: \[\left.r_{,_{t}}^{2}\right|_{(t=0)}=0\] (19) A nonzero initial velocity is considered in Appendix A. We note that in all cases, the choice of initial conditions is not arbitrary and must satisfy constraints imposed by (5) and (7). These equations do not contain second time derivatives and, as is well known (see [27]), under the condition that \({t={\rm\,const}}\) at the initial cross section, they are automatically satisfied for all values \(t\) by virtue of the other Einstein equations. We choose the initial coordinate scale of \(R\) in (4) such that \[r_{i}=\sqrt{q^{2}+R^{2}}\,,\qquad\varepsilon_{di}\equiv\varepsilon_{d}(r_{i})= -\frac{q^{2}}{4\pi r_{i}^{4}}\,.\] (20) where \({r_{i}(R)}\) coincides with (1) and Eqn (10) is automatically satisfied. We set \[s(r_{i})\equiv\frac{1}{r_{i}}\int\limits_{0}^{R}8\pi(\varepsilon_{i}- \varepsilon_{di})r_{i}^{2}r_{i,_{R}}\,dR=\frac{1}{r_{i}}\int\limits_{q}^{r_{i} }8\pi\varepsilon_{i}r_{i}^{2}\,dr_{i}+2\frac{q}{r_{i}}\left(1-\frac{q}{r_{i}}\right)\] (21) The quantity \(s\) has the meaning of the doubled Newtonian potential of dust matter excessive relative to \(\varepsilon_{d}\) [see (20)]. The relation of this potential to the functions \(F_{1}\) and \(F_{2}\) follows from (15) and (16) at the initial instant: \[F_{1}=1-s-\frac{q^{2}}{r_{i}^{2}}-\frac{\Lambda}{3}\left(r_{i}^{2}-q^{3}/r_{i} \right)\,,\] (22) \[F_{2}=r_{i}\left(s+2\frac{q^{2}}{r_{i}^{2}}-\frac{\Lambda q^{3}}{3r_{i}}\right )\,.\] (23) Equation (9) implies that \({F_{1}\geq 0}\). According to (22), this imposes constraints on the distribution \({s(R)}\). From Eqn (6), we can find \({r_{,_{tt}}}\) at the initial instant: \[\makebox{at }t=0\,:\quad r_{,_{tt}}=-\frac{s}{2r_{i}}+\frac{\Lambda r_{i}}{3}+ \frac{\Lambda q^{3}}{6r_{i}^{2}}\] (24) Equation (24) shows that for \({\Lambda=0}\), the dynamics are absent in the region were \({s=0}\) (at least up to the instant of intersection of the dust layers, when the model considered becomes inapplicable). ## 4 Solution without the \(\Lambda\)-term We consider the case \({\Lambda=0}\) in more detail. For \({\Lambda=0}\), it follows from Eqn (24) that **the WH throat size remains constant \({[r_{{}_{0}}(t)=q]}\) in the whole region of the allowed values of \(R\) and \(t\) for the sought solution, until matter starts flowing through the throat. In addition, expression (24) implies that the dynamics of matter in a WH depend only on the internal layers of matter (with smaller values of r) and are independent of the external layers. Therefore, matter on one side of the throat does not influence matter on the opposite side (unless there is matter flowing through the throat or layer intersection occurs).** It can be verified directly from (24) that at the initial instant, the acceleration \({r_{,_{tt}}}\) is negative for \({s>0}\). Hence, the excessive mass of dust is to collapse. We introduce the definition of the apparent horizon. [FIGURE:S4.F1][ENDFIGURE] **The criterion of the absence of a apparent horizon during the collapse is given by** \[V<1\] (25) for the dust velocity [see also [23],[29],[30],[24] and (12)], where the dust velocity \(V\) is determined as \[V^{2}\equiv r_{,_{t}}^{2}e^{\lambda}/r_{,_{R}}^{2}=r_{,_{t}}^{2}/F_{1}=\frac{( s+2q^{2}/r_{i}^{2})r_{i}/r-s-q^{2}/r_{i}^{2}-q^{2}/r^{2}}{1-s-q^{2}/r_{i}^{2}}\] (26) For \({q=0}\), this result coincides with the solution for collapsing dust (see [23]). To avoid a \({0/0}\) ambiguity for the function \(V^{2}\) at the throat at the initial instant \({(F_{1}[r_{i}\to r_{{}_{0}}]\to 0)}\), it is necessary to ensure a more rapid convergence to zero of the function \({r_{,_{t}}^{2}(t=0,r_{i}\to r_{{}_{0}})}\) than the function \({F_{1}(r_{i}\to r_{{}_{0}})}\) (see Appendix A). [FIGURE:S4.F2][ENDFIGURE] The law of motion of a dust layer can be found from (12): \[t=\int\limits_{r_{i}}^{r}\frac{-r\,dr}{\sqrt{(F_{1}-1)r^{2}+F_{2}r-q^{2}}}= \int\limits_{r_{i}}^{r}\frac{-r\,dr}{r_{i}\sqrt{(1-r/r_{i})[(s+q^{2}/r_{i}^{2} )r/r_{i}-q^{2}/r_{i}^{2}]}}\] (27) This quadrature can be elementarily integrated: \[t=r_{i}\frac{\sqrt{(1-r/r_{i})[(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}]}}{s +q^{2}/r_{i}^{2}}+r_{i}\frac{s+2q^{2}/r_{i}^{2}}{2(s+q^{2}/r_{i}^{2})^{3/2}} \cdot\arccos\left[1-\frac{2(s+q^{2}/r_{i}^{2})(1-r/r_{i})}{s}\right]\] (28) or in another form, \[t=r_{i}\left[\frac{\sqrt{(1-r/r_{i})[(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2 }]}}{s+q^{2}/r_{i}^{2}}+\frac{s+2q^{2}/r_{i}^{2}}{(s+q^{2}/r_{i}^{2})^{3/2}} \cdot{\rm\,arctg}\sqrt{\frac{(s+q^{2}/r_{i}^{2})(1-r/r_{i})}{(s+q^{2}/r_{i}^{2 })r/r_{i}-q^{2}/r_{i}^{2}}}\right]\] (29) **Hence, the motion of dust layers depends on the excessive potential \(s\) and the initial distance from the WH throat: \(r_{i}/q\).** However, this model is physically correct only until a possible intersection of dust layers. This is because after the intersection, an incoming energy flux appears in the matter-comoving frame (from the intersected matter layers), which has not been taken into account in the energy-momentum tensor. The intersection of adjacent matter layers corresponds to an infinite energy density. This corresponds to the condition \({r_{,_{R}}=0}\) (or \({\frac{dr}{dr_{i}}=0}\)) [see (20)]. Differentiation of (29) with respect to \({r_{i}}\) allows explicitly determining the function \({\frac{dr}{dr_{i}}(r,s,q)}\). Differentiation of the left-hand side of (29) yields zero. We let a prime denote the derivative with respect to \(r_{i}\), express all distances in the units of units \(r_{i}\), and omit intermediate bulky calculations; the final expression for this function is given by \[r^{\prime}=1+\frac{(1-r)\left[s(s^{\prime}-2q^{2})(2q^{2}-r\{s+q ^{2}\})-q^{2}(s+2q^{2})(2s^{\prime}+s)\right]}{2rs(s+q^{2})^{2}}+\] \[+\frac{\left[2s(s+q^{2})+(2q^{2}-s^{\prime})(s+4q^{2})\right] \sqrt{(1-r)[(s+q^{2})r-q^{2}]}}{2r(s+q^{2})^{5/2}}\cdot{\rm\,arctg}\sqrt{\frac {(s+q^{2})(1-r)}{(s+q^{2})r-q^{2}}}\] (30) It is impossible to use this formula to determine the instant of intersection of nonadjacent layers because the intersection with nonadjacent layers does not lead to any irregularities for dust. Clearly, the intersection of nonadjacent layers occurs after the intersection of adjacent ones and cannot propagate with a superluminal velocity. Therefore, after constructing diagrams \(t(r_{i})\) for light cones and the curve corresponding to the intersection of adjacent layers \({(r^{\prime}=0)}\), we can determine regions that are definitely free from layer intersection (see the Figure 1 or 2). Using formula (26), we can reach several important conclusions. **1. The formation of a horizon is possible only for a sufficiently large parameter \(s\):** \[s>2\frac{q}{r_{i}}\left(1-\frac{q}{r_{i}}\right)\] (31) **After the appearance of a horizon, the WH becomes ”non-traversable”.** However, dust layers can already start intersecting before the horizon is reached. **2. Values of the function \({t(r,r_{i})}\) are bounded by the maximum time \(t_{stop}\) (from the beginning of motion until the stop).** In (28), this time corresponds to the argument of \({\bf\arccos}\) being minus unity (or to the zero value of the square root expression in the same formula): \[t_{stop}=\frac{\pi r_{i}(s+2q^{2}/r_{i}^{2})}{2(s+q^{2}/r_{i}^{2})^{3/2}}\] (32) The time \(t_{stop}\) corresponds to the deviation \({\Delta r\approx sr_{i}^{3}/q^{2}}\) from the initial position. **For small deviations (corresponding to small values of \(s\)), harmonic oscillations with the period \({T=2t_{stop}\approx 2\pi r_{i}^{2}/q}\) occur** (see Appendix B). **3. The existence of the second (smaller) root of the equation \({V^{2}(r)=1}\) implies the appearance of the second (inner) horizon in the system (see the Figures 1 and 2).** 4. For parameter \({s=2q(1-q/r_{i})/r_{i}}\) (or \({\varepsilon=0}\)) the scalar \({\bf g^{ik}\,r_{;i}r_{;k}=(1-q/r)^{2}}\) (scalar equal to the scalar of the extremal Reisner-Nordstrem solution). Therefore: **if the energy density tends to zero — the solution (29) tends to the extremal Reisner-Nordstrem solution of black hole (in the comoving, free-falling frame).** ## 5 Solution for \(s=0\) with the \(\Lambda\)-term We consider the case where \(s=0\). Eqn (6) with (9) and (22) then becomes \[2rr_{,_{tt}}=\Lambda r^{2}+q^{2}\left(\frac{1}{r^{2}}-\frac{1}{r_{i}^{2}} \right)-\frac{\Lambda}{3}\left(r_{i}^{2}-q^{3}/r_{i}\right)-r^{2}_{,_{t}}\,,\] (33) and Eqn (12) takes the form \[r^{2}_{,_{t}}=(r-r_{i})\left[-\frac{q^{2}}{r^{2}r_{i}^{2}}(r-r_{i})+\frac{ \Lambda}{3}\left(r+r_{i}+\frac{q^{3}}{rr_{i}}\right)\right]\,.\] (34) These two equations imply that at \(s=0\), matter starts expanding from the rest state (see 19): inflation due to the \(\Lambda\)-term). **If the dimensionless parameter** \[a\equiv\Lambda q^{2}\] (35) **exceeds some critical value \({a_{cr}}\), the inflation continues unlimitedly in the entire volume \({(q\leq r_{i}\leq r<\infty)}\) until an outer horizon forms, \({V^{2}(r)=1}\).** The value \({a_{cr}}\) is found from the condition of the maximum of the expression for the parameter \(a\), which is obtained by equating the second factor (in square brackets) in Eqn (34) to zero: \[a_{cr}=MAX\left[\frac{3\tilde{q}^{4}(1-\tilde{r})\tilde{r}^{2}}{1+\tilde{r}+ \tilde{r}^{2}\tilde{q}^{3}}\right]\approx 0.22\,,\quad\tilde{r}\equiv r_{i}/r \,,\quad\tilde{q}\equiv q/r_{i}\,.\] (36) **For \({a<a_{cr}}\), a region appears where the inflation stops.** This region starts emerging at the throat and extends toward larger values of \(r_{i}\) as the parameter \(a\) decreases. **As \({r/r_{i}\to\infty}\), the inflation occurs exponentially: \({r\propto\exp(t\sqrt{\Lambda/3})}\).** The function \(r^{\prime}\) can be expressed in quadratures (see Appendix C): \[r^{\prime}=1+\sqrt{r-r_{i}}\exp\left(-\int\limits_{r_{i}}^{r}P_{ 2}(x)\,dx\right)\cdot\int\limits_{r_{i}}^{r}\frac{Q_{2}(r)-P_{2}(r)}{\sqrt{r-r _{i}}}\exp\left(\int\limits_{r_{i}}^{r}P_{2}(x)\,dx\right)\,dr\,,\] \[P_{2}=\frac{\frac{r_{i}^{2}}{2r^{2}}-\frac{r_{i}^{2}(r-r_{i})}{r ^{3}}-\frac{a}{2}\left(1-\frac{q^{3}}{r^{2}r_{i}}\right)}{-\frac{r_{i}^{2}(r-r _{i})}{r^{2}}+a\left(r+r_{i}+\frac{q^{3}}{rr_{i}}\right)}\,,\quad Q_{2}-P_{2}= \frac{a+(r+r_{i})\left(\frac{r_{i}(r-r_{i})}{r^{3}}-\frac{aq^{3}}{2r^{2}r_{i}^ {2}}\right)}{-\frac{r_{i}^{2}(r-r_{i})}{r^{2}}+a\left(r+r_{i}+\frac{q^{3}}{rr_ {i}}\right)}\,.\] (37) Using this equation, we can find regions where the inflation occurs without dust layer intersections. ## 6 Model of the Multiverse Dust with the positive \(s\) initially accelerates toward the center (without the \(\Lambda\)-term). The \(\Lambda\)-term without excessive dust leads to the original inflationary solution [see (24)]. At the WH throat, the potential \(s=0\), and the \(\Lambda\)-term at the throat provides nonzero matter acceleration. This contribution cannot be compensated at or near the throat [see (6)], where \({r_{,_{t}}=r_{,_{tt}}=0}\) and \({r=q}\). Hence, there is no static solution for a WH with the throat radius \({r_{{}_{0}}=q}\) and the \(\Lambda\)-term. Nevertheless, a static solution exists for a WH with the \(\Lambda\)-term and \({r_{{}_{0}}\neq q}\). This solution can be easily derived from Eqns (5), (6) and (8) (with \({r_{,_{t}}=0}\) and \({r_{,_{tt}}=0}\)). The metric of a static WH is determined by expression (1), taking into account that \({r^{2}(R)\neq q^{2}+R^{2}}\). From (6), we obtain \({r_{,_{R}}^{2}=1-q^{2}/r^{2}-\Lambda r^{2}}\) and easily find the expression for the throat radius \({r_{{}_{0}}}\), \[\Lambda r_{{}_{0}}^{4}-r_{{}_{0}}^{2}+q^{2}=0\quad\Rightarrow\quad r_{{}_{0}}^ {2}=\frac{1-\sqrt{1-4\Lambda q^{2}}}{2\Lambda}\to q^{2}(1+\Lambda q^{2})\qquad (\makebox{at }\Lambda q^{2}\to 0)\,,\] (38) and the dependence \({r(R)}\): \[r^{2}(R)=\frac{1-\sqrt{1-4\Lambda q^{2}}\cdot\cos(2\sqrt{\Lambda}R)}{2\Lambda}\] (39) The distribution of \(\varepsilon\) for this solution is determined⁷ from (5): [FOOTNOTE:7][ENDFOOTNOTE] \[\varepsilon=\frac{\Lambda}{4\pi}-\frac{q^{2}}{4\pi r^{4}}\] (40) Thus, for the static solution with the \(\Lambda\)-term, the throat radius and dust density are larger than without the \(\Lambda\)-term. The total energy density for the static solution with the \(\Lambda\)-term is \[T^{t}_{t}=\frac{3\Lambda}{8\pi}-\frac{q^{2}}{8\pi r^{4}}\] (41) The condition for the value \({T^{t}_{t}}\) to be nonnegative everywhere in space (for \({r\geq r_{{}_{0}}}\)) has the form \[T^{t}_{t}\geq 0\quad\makebox{at }a=\Lambda q^{2}\geq\frac{3}{16}\] (42) **Therefore, in the presence of the \(\Lambda\)-term, solutions for wormholes with a positive total energy density can be found.** From (39), we can obtain the maximum allowed radius of the static metric with the \(\Lambda\)-term: \[r_{max}^{2}=\frac{1+\sqrt{1-4\Lambda q^{2}}}{2\Lambda}\to\frac{1}{\Lambda} \qquad(\makebox{at }\Lambda q^{2}\to 0)\,.\] (43) Beyond this radius, the Universe starts contracting again until a new throat occurs. **Solution (39) describes a static Multiverse with an infinite number of throats. When there is no charge \({(q=0)}\), this solution becomes a cosmological solution without wormholes, corresponding to a closed isotropic universe** (see §112, [31]). When there is an excess (or shortage) of the dust part of the energy density or the \(\Lambda\)-term relative to (40), the obtained solution for the Multiverse becomes dynamical. Its analytic study is complicated by the need to solve a fourth-order algebraic equation and to calculate a quadrature similar to (37) for the instant of dust layer intersection. ## 7 Conclusion In this paper, we have generalized and developed the method suggested earlier in papers [20], [22] and applied it to new problems in modern cosmology. We found and analyzed analytic solutions of the general relativity equations describing the dynamics of a traversable wormhole. The results obtained are important for the analysis of the general properties of traversable wormholes. We also obtained a solution describing a spherically symmetric model of the Multiverse. We have not analyzed the properties of geodesics that describe the motion of particles and other matter (energy and information) through a wormhole and its vicinity. These problems, which are mostly important for the analysis of the possible observational appearance of such objects, are considered elsewhere (see, e.g., [11]). To conclude, we remark on the term ”Multiverse”. This term is used in physics and cosmology in two different senses. First, this term assumes the possibility of the parallel co- existence of many or even an infinite number of different worlds, possibly emerged from a quantum vacuum (in some sense, in different places at different times). In this paper, this term is used exactly in this sense. Second, this term is sometimes used to denote a sample of different realities in the Everett interpretation of quantum mechanics. The usage of one term for different notions is sometimes confusing. In our opinion, different terms should be used for these concepts. We propose keeping the term ”Multiverse”  for cosmology, and refer to the set of Everett worlds (following the proposal by M.B. Mensky) as the ”Alterverse”, keeping in mind different classical alternatives of the Everett world. ## 8 Acknowledgments We are grateful to the staff of the theoretical astrophysics department of the Lebedev Physical Institute for the discussions. The work is supported by the RFBR grants \({07-02-01128a}\) and \({08-02-00090a}\), grants of scientific schools \({NSh-626.2008.2}\) and \({NSh-2469.2008.2}\), and the program of the Russian Academy of Sciences, ”The Origin and Evolution of Stars and Galaxies 2008”. ## Appendix A Initial conditions with a nonzero velocity At the WH throat, the expression for \(V^{2}\) in (26) involves a \({0/0}\) ambiguity. To resolve this ambiguity, we consider the model with a nonzero initial velocity of matter. We introduce the notation \[1-q/r_{i}\equiv\alpha\,,\quad r_{i}/r-1\equiv\beta\,,\quad\left.r_{,_{t}}^{2} \right|_{(t=0)}\equiv\gamma\,.\] (44) and assume that \({\Lambda=0}\). The expressions for the functions \(F_{1}\) and \(F_{2}\) with \({\gamma\neq 0}\) [see (15) and (12)] are given by \[F_{1}=1-s-q^{2}/r_{i}^{2}+\gamma-\gamma_{{}_{0}}q/r_{i}\,,\quad F_{2}=r_{i} \left[s+2q^{2}/r_{i}^{2}+\gamma_{{}_{0}}q/r_{i}\right]\,.\] (45) With (12) and a nonzero initial velocity, the expression for \(V^{2}\) in (26) takes the form \[V^{2}=\frac{-s-q^{2}/r_{i}^{2}+\gamma-\gamma_{{}_{0}}q/r_{i}+(s+2q^{2}/r_{i}^{ 2}+\gamma_{{}_{0}}q/r_{i})r_{i}/r-q^{2}/r^{2}}{1-s-q^{2}/r_{i}^{2}+\gamma- \gamma_{{}_{0}}q/r_{i}}\] (46) In the vicinity of the WH throat close to the initial instant, the functions \(\alpha\) and \(\beta\) take small values. From (21), in the linear order in \(\alpha\), we have \[s\approx\alpha\kappa\,,\quad\kappa=8\pi r_{i}^{2}(\varepsilon_{i}-\varepsilon_ {d})\approx 8\pi\varepsilon_{{}_{0}}q^{2}+2<2\,.\] We consider Eqn (46) in the linear order in \(\alpha\) and \(\beta\). After all transformations, we finally obtain \[V^{2}\approx\frac{\gamma+\gamma_{{}_{0}}\beta}{\gamma-\gamma_{{}_{0}}(1-\alpha )+\alpha(2-\kappa)}\to\frac{\gamma_{{}_{0}}(1+\beta)}{\alpha(\gamma_{{}_{0}}+2 -\kappa)}\makebox{ at }\gamma\to\gamma_{{}_{0}}\,.\] (47) It follows that the condition for \(V^{2}\) to be nonsingular at the throat is that \({\gamma_{{}_{0}}=0}\). Then \[V^{2}\approx\frac{\gamma}{\gamma+\alpha(2-\kappa)}\] (48) Expression (48) for \(V^{2}\) is regular and has no ambiguities if the function \(\gamma\) tends to zero at the throat faster than the function \(\alpha\). In this case, the rate of change of the radius \(r\) vanishes at the throat (as must be the case by the definition of the throat). In the linear order in \(\beta\), the function \(V^{2}\) is time-independent near the throat. ## Appendix B Study of intersections of adjacent layers We consider the model without the \(\Lambda\)-term for \(s>0\). In this case, the excessive matter collapses, i.e., \({r\leq r_{i}}\). **Lemma. There always exists a nonzero time interval \({[0,t]}\) inside which no intersections of adjacent layers occur.** Equation (30) implies that this is obvious for a nonzero potential \({s}\). The only point at which this statement must be proved is the point corresponding to \({s=0}\). We study the asymptotic regime \({s\to 0}\) in more detail: \[s<<q^{2}/r_{i}^{2}\leq 1\] (49) From the allowed range of the radius (until the stopping point) \({r\geq q^{2}/(sr_{i}+q^{2}/r_{i})}\), we deduce \[1-\frac{r}{r_{i}}\leq\frac{s}{s+q^{2}/r_{i}^{2}}\leq\frac{s}{q^{2}/r_{i}^{2}}<<1\] (50) Because the last term in (30) contains no \(s\) in the denominator, it can be neglected compared to the previous term. This can be proved in more detail by considering the there exhaustive options for the ratio of the numerator and denominator in the square root expression of the \({\bf\arctan}\): 1. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})<<(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) 2. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})\sim(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) 3. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})>>(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) Keeping the leading terms, we obtain the asymptotic form of Eqn (30): \[r^{\prime}\to 1+\frac{(1-r/r_{i})[-q^{2}\cdot 2q^{2}\cdot 2r_{i}s^{\prime}]}{2 sq^{4}}=1-2r_{i}s^{\prime}(1-r/r_{i})/s\] (51) In a similar way, the first term in the right-hand side of expression (28) can be neglected (compared to the second term), and hence asymptotically with respect to time, we have \[\cos\left(\frac{tq}{r_{i}^{2}}\right)\to 1-\frac{2q^{2}}{sr_{i}^{2}}(1-r/r_{i} )\quad\Longrightarrow\quad r\to r_{i}+\frac{sr_{i}^{3}}{2q^{2}}\left[\cos\left (\frac{tq}{r_{i}^{2}}\right)-1\right]\] (52) Comparing Eqns (51) and (52), we obtain the sought asymptotic form as \({s\to 0}\): \[r^{\prime}\to 1-\frac{2r_{i}^{3}s^{\prime}}{q^{2}}\sin^{2}\left(\frac{tq}{2r_{ i}^{2}}\right).\] (53) This proves the lemma. In addition, Eqn (52) implies harmonic dynamics (oscillations) for \({s\to 0}\) and \({2r_{i}^{3}s^{\prime}/q^{2}<1}\). ## Appendix C Quadrature for \(r^{\prime}\) in the solution with the \(\Lambda\)-term We differentiate \(r_{,_{t}}^{2}\) with respect to \(r_{i}\): \[\frac{dr_{,_{t}}^{2}}{dr_{i}}=2r_{,_{t}}r^{\prime}_{,_{t}}=2r_{,_{t}}^{2}\frac {dr^{\prime}}{dr}\quad\Rightarrow\quad\frac{dr^{\prime}}{dr}=\frac{1}{2r_{,_{t }}^{2}}\cdot\frac{dr_{,_{t}}^{2}}{dr_{i}}\] (54) Substituting Eqn (34) in (54) and differentiating it with respect to \(r_{i}\), we obtain the following equation for the function \({y(r)\equiv r^{\prime}}\): \[\frac{dy}{dr}+P(r)y=Q(r)\,,\] (55) Here, the functions \({P(r)\equiv P_{1}(r)+P_{2}(r)}\) and \({Q(r)\equiv Q_{1}(r)+Q_{2}(r)}\) are given by (for convenience, \(r_{i}\) is set to unity below): \[P_{1}=\frac{-1}{2(r-1)}\,,\quad P_{2}=\frac{1/(2r^{2})-(r-1)/r^{ 3}-(a/2)(1-q^{3}/r^{2})}{(1-r)/r^{2}+a(1+r+q^{3}/r)}\,,\] \[Q_{1}=\frac{-1}{2(r-1)}\,,\quad Q_{2}=\frac{1/(2r^{2})+(r-1)/r^{ 2}+(a/2)(1-q^{3}/r)}{(1-r)/r^{2}+a(1+r+q^{3}/r)}\,.\] (56) Equation (55) has a standard solution, \[y(r)=\exp\left[-\int\limits_{r_{1}}^{r}P(x)\,dx\right]\cdot\left\{\int\limits_ {r_{2}}^{r}Q(r)\cdot\exp\left[+\int\limits_{r_{1}}^{r}P(x)\,dx\right]\,dr+C_{1 }\right\}\] (57) The constants \(C_{1}\), \(r_{1}\) and \(r_{2}\) are determined by the initial conditions. The exponential can be rewritten as (the first term with \(P_{1}\) is integrated): \[\exp\left[\int\limits_{r_{1}}^{r}P(x)\,dx\right]=\frac{C_{2}}{\sqrt{r-1}}\cdot \exp\left[\int\limits_{1}^{r}P_{2}(x)\,dx\right]\] (58) After that, the part of integral (57) corresponding to \(Q_{1}\) can also be integrated (by parts), with the result \[y(r)=\sqrt{r-1}\cdot\exp\left[-\int\limits_{1}^{r}P_{2}(x)\,dx \right]\cdot\left\{\frac{1}{\sqrt{r-1}}\cdot\exp\left[+\int\limits_{1}^{r}P_{2 }(x)\,dx\right]\right|_{r_{2}}^{r}-\] \[\left.-\int\limits_{r_{2}}^{r}\frac{P_{2}(r)}{\sqrt{r-1}}\cdot \exp\left[+\int\limits_{1}^{r}P_{2}(x)\,dx\right]\,dr+\int\limits_{r_{2}}^{r} \frac{Q_{2}(r)}{\sqrt{r-1}}\cdot\exp\left[+\int\limits_{1}^{r}P_{2}(x)\,dx \right]\,dr+C_{1}\right\}\] (59) We can then redefine the lower integration limit and determine the constant \(C_{1}\) from the initial conditions. The final expression for the function \({y(r)=r^{\prime}}\) is given in (37). ## References * [1] S.W. Hawking, _Black Holes and the Structure of the Universe_, Eds. by C. Teitelboim and J. Zanelli (World Sci., Singapore, 2000), p.23. * [2] F.S. Lobo, Phys.Rev., **D71**, 084011, (2005) * [3] H. Shinkai, S.A. Hayward, Phys.Rev., **D66**, 044005, (2002) * [4] M.S. Morris, K.S. Thome, Am. J. Phys., **56**, 395, (1988) * [5] Novikov I.D., Zh. Eksp. Teor. Fiz., **95**, 769, (1989) [Sov. Phys. JETP 68 439 (1989)] * [6] I.D. Novikov, Phys.Rev. **D45**, 1989, (1992) * [7] S.W. Hawking, Phys.Rev., **D46**, 603, (1992) * [8] M. Visser, _Lorentzian Wormholes: from Einstein to Hawking_, (Woodbury, NY: AIP, 1995) * [9] Shatskii A., Astron. Zh., **81**, 579, (2004) [Astron. Rep. 48 525 (2004)] * [10] Shatskii A., Astron. Zh., **84**, 99, (2007) [Astron. Rep. 51 81 (2007)] * [11] Kardashev N.S., Novikov I.D., Shatskii A., Astron. Zh., **83**, 675, (2006) [Astron. Rep. 50 601 (2006)] * [12] N.S. Kardashev, I.D. Novikov, A. Shatskiy, Int. J. Mod. Phys **D16**, 909, (2007) * [13] Novikov I.D., Kardashev N.S., Shatskii A., Usp. Fiz. Nauk, **177**, 1017, (2007) [Phys. Usp. 50 965 (2007)] * [14] Cherepashchuk A.M., Vestn. Mosk. Gos. Univ., Ser. 3, Fiz. Astron. **(2)**, 62, (2005) [Moscow Univ. Phys. Bull. 60 (2) 74 (2005)] * [15] Bronnikov K.A, Starobinsky A.A., Pis’ma Zh. Eksp. Teor. Fiz., **85**, 3, (2007) [JETP Lett. 85 1 (2007)]; gr-qc/0612032 * [16] V.P. Frolov, I.D. Novikov, _Black Hole Physics. Basic Concepts and New Developments_, Kluver AP, (1998) * [17] Armendariz-Picon C., gr-qc/0201027, (2002) * [18] B. Carr, editor, _Universe or Multiverse?_, Cambridge Univ. Press, (2007) * [19] H.G. Ellis, J. Math. Phys., **14**, 104, (1973) * [20] R.C. Tolman, Proc. Nat. Acad. Sci. US, **20**, 169, (1934) * [21] J.R. Oppenheimer, H. Snyder, Phys. Rev., **56**, 455, (1939) * [22] R. Saibal, D. Basanti, R. Farook, et al., Int. J. Mod. Phys, **D16**, No11, pp.1745-1759, (2007) * [23] Shatskii A., Andreev A.Yu., Zh. Eksp. Teor. Fiz., **116**, 353, (1999) [JETP 89 189 [1999)] * [24] Shatskii A., Zh. Eksp. Teor. Fiz., **131**, 851, (2007) [JETP 104 743 (2007)] * [25] Shatskiy A., Novikov I.D., Kardashev N.S., Physics-Uspekhi, **51**, (5) pp. 457-464, (2008) * [26] I. Fisher, _Scalar mesostatic field with regard for gravitational effects_, Zhurnal Experimental’noj Teoreticheskoj, **18**, 636, (1948) * [27] A. Janis, E. Newman, J. Winicour, _Reality of the Schwarzschild Singularity_, Phys. Rev. Lett., **20**, 878, (1968) * [28] M. Wyman, _Static spherically symmetric scalar fields in general relativity_, Phys. Rev. **D24**, 839, (1981) * [29] Novikov I.D., Vestnik Mosk. Gos. Univ., Ser. 3, Fiz. Astron., **6**, p.61, (1962) * [30] Zel’dovich Ya.B., Novikov I.D., _Relyativistskaya Astrofizika_, Moscow: Nauka, (1967) [Translated into English: Relativistic Astrophysics Vol. 1 Stars and Relativity (Chicago: Univ. of Chicago Press, 1971)] * [31] Landau L.D., Lifshitz E.M., Teoriya Polya, _The Classical Theory of Fields_, Moscow: Nauka, (1988) [Translated into English (Oxford: Pergamon Press, 1983)]

# Новые аналитические модели "проходимых" червей ###### Аннотация Даны аналитические решения уравнений общей теории относительности для сферически симметричных червоточин. Мы исследуем особый случай "проходимой" червоточины, то есть такой, через которую сигнал может проходить. Тензор энергии-импульса вещества червоточины представлен как суперпозиция сферически симметричного магнитного поля и пылевого вещества с отрицательной плотностью материи. Исследуются динамика модели. Обсуждается как решение уравнения с термином \(\Lambda\), так и без него. Путем достаточной суперпозиции пылевого вещества, магнитного поля и термина \(\Lambda\) можно получить статическое решение, которое оказывается сферической моделью Мультивселенной с бесконечным количеством червоточин, соединяющих сферические вселенные. Соответствующее решение может быть статическим и динамическим. Александр Шатский\(^{1}\), И.Д. Новиков\(^{1,2,3}\), Н.С. Кардашёв\(^{1}\) \({}^{1}\)Астрономический космический центр, Физический институт им. Лебедева, Москва, Россия, [email protected] \({}^{2}\)Институт Нильса Бора, Blеdгамсвед 17, DK-2100 Копенгаген, Дания \({}^{3}\)Курчатовский институт, Москва, Россия ## 1 Введение Червоточина (ЧТ) [1]-[19]) - гипотетический объект, описываемый недиссонантным решением уравнений Эйнштейна, имеющим два больших (или бесконечных) пространственно-временных региона, соединенных горлом. Два больших пространственно-временных региона могут находиться в одной вселенной или принадлежать разным вселенным в модели Мультвселенной (см. [18]). В последнем случае "проходимые" ЧТ предоставляют уникальную возможность исследовать другие вселенные. В данной статье мы аналитически изучаем динамику сферической модели неэквилибриальной ЧГ, заполненной веществом. Это вещество состоит из магнитного поля и пыли с отрицательной плотностью массы. Полученное решение обобщает решение Толмана [20] для модели с сферически симметричным электромагнитным полем. Как мы увидим далее, эта обобщенная модель приводит к существенно новым и важным решениям. Мы использовали метод расчета физических величин в системе, передвигающейся вместе с пылью. В качестве исходной модели для черных дыр мы используем статическую модель, в которой гравитационные ускорения везде одинаково равны нулю. Таким образом, эффективные массы обоих рот черных дыр обращаются в ноль, хотя геометрия трехмерного пространства явно неевклидова. Такая модель рассматривается в [19] и [17], где вся материя представлена гравитирующим скалярным полем. Мы изменяем скалярное поле в суперпозицию электромагнитного поля и пыли с отрицательной энергетической плотностью, что оказывается методологически важным развитием и обобщением этих моделей. Это позволяет нам применять методы проблемы Толмена для расчета модели (см. [20], [21], [22]); эти методы были обобщены и дальше развиты Шатский (см. [23] и [24]). Для дальнейшей обобщения и развития этого метода, мы вводим космологический термин \(\Lambda\) в модель. Это позволяет получить принципиально новое решение (см. Раздел 6) для статической сферической модели Мультивселенной. Эта модель включает бесконечное количество сферических миров, соединенных горлами. На нашем сведении, это первая аналитическая модель такого типа. В полученном решении Мультимир может иметь положительную плотность энергии везде в пространстве. Кроме того, это решение может быть обобщено с использованием того же метода на случай динамической модели, сдвинутой из равновесия избытком (или нехваткой) пыли или через \(\Lambda\)-термин. Некоторые методологические детали можно найти в [25]. ## 2 уравнения Эйнштейна Мы используем статическое сферически-симметрическое решение уравнений Эйнштейна Армендариз-Пикона [17] для описания непертурбированной модели WH¹. [FOOTNOTE:1] Переведено с сохранением формул: \[\ ds^{2}=dt^{2}-dR^{2}-r^{2}(d\theta^{2}+\sin^{2}\theta\,d\varphi^{2})\,,\quad r ^{2}(R)=q^{2}+R^{2}\,. \] (1) Минимально допустимый радиус этой черной дыры составляет \({r_{{}_{0}}=q}\) (радиус глотки²). [FOOTNOTE:2][ENDFOOTNOTE] Обычно эта решение связано с тензором энергии-импульса скалярного поля (см. [19], [17]). В данной статье мы предлагаем другую интерпретацию этого решения, связанную с другим представлением тензора энергии-импульса. Эта новая интерпретация решения (1) может соответствовать тензору энергии-импульса, представленному как \[T^{n}_{k}=\left(\begin{tabular}[]{c c c c}$-\frac{q^{2}}{8\pi r^{4}}$&0&0&0\\ 0&$+\frac{q^{2}}{8\pi r^{4}}$&0&0\\ 0&0&$-\frac{q^{2}}{8\pi r^{4}}$&0\\ 0&0&0&$-\frac{q^{2}}{8\pi r^{4}}$\\ \end{tabular}\right)=\left(\begin{tabular}[]{c c c c}$+\frac{q^{2}}{8\pi r^{4} }$&0&0&0\\ 0&$+\frac{q^{2}}{8\pi r^{4}}$&0&0\\ 0&0&$-\frac{q^{2}}{8\pi r^{4}}$&0\\ 0&0&0&$-\frac{q^{2}}{8\pi r^{4}}$\\ \end{tabular}\right)+\left(\begin{tabular}[]{c c c c}$-\frac{q^{2}}{4\pi r^{4} }$&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{tabular}\right)\] (2) Первое слагаемое в правой части соответствует тензору энергии-импульса статического магнитного поля с эффективным магнитным зарядом \(q\), а второе слагаемое описывает пылевое вещество с отрицательной плотностью энергии. \[\varepsilon_{d}=-\frac{q^{2}}{4\pi r^{4}}\] (3) \[\varepsilon_{d}=-\frac{q^{2}}{4\pi r^{4}}\] (3) Это возможное представление тензора \({T^{n}_{k}}\) отличается от его эквивалентного представления в виде тензора энергии-импульса скалярного поля, принятого в предыдущих статьях [17]-[28]. Избыток (или дефицит) пыли (относительно \({\varepsilon_{d}}\)) не находится в равновесии и инициирует движение. Поскольку слои пыли относительно независимы, можно проинтегрировать уравнения движения для пыли аналогично решению проблемы Толмена [20]. По сути, это то же самое, что и проблема Толмена в центрально-симметричном и статическом электрическом (или магнитном) поле для нейтральной пыли. Мы ищем метрический тензор решения в форме³: [FOOTNOTE:3][ENDFOOTNOTE] перевести разметку с английского на русский. Сохранить формулы: \[ds^{2}=dt^{2}-e^{\lambda}dR^{2}-r^{2}(d\theta^{2}+\sin^{2}\theta\,d\varphi^{2}),\] (4) can be translated to Russian as: \[ ds^{2} = dt^{2} - e^{\lambda}dR^{2} - r^{2}(d\theta^{2}+\sin^{2}\theta\,d\varphi^{2}),\] (4) где \(r^{2}\) и \(e^{\lambda}\) являются функциями как \(R\), так и \(t\). Ниже мы обосновываем это выбор метрики. Мы рассматриваем проблему в присутствии терма \(\Lambda\). Уравнения Эйнштейна, соответствующие метрике (4), могут быть записаны таким образом⁴: [FOOTNOTE:4][ENDFOOTNOTE] - [СНОСКА:4][КОНЕЦ_СНОСКА] \[ 8\pi T_{t}^{t}=8\pi\varepsilon+q^{2}/r^{4}+\Lambda=-e^{-\lambda} \left(2rr_{,_{RR}}+r^{2}_{,_{R}}-rr_{,_{R}}\lambda_{,_{R}}\right)/r^{2}+\left( rr_{,_{t}}\lambda_{,_{t}}+r^{2}_{,_{t}}\right)/r^{2}+1/r^{2}\,,\] (5) \[ 8\pi T_{R}^{R}=q^{2}/r^{4}+\Lambda=\left(2rr_{,_{tt}}+r^{2}_{,_{ t}}\right)/r^{2}-e^{-\lambda}r^{2}_{,_{R}}/r^{2}+1/r^{2}\,,\] (6) \[ 8\pi T^{R}_{t}=0=e^{-\lambda}\left(2r_{,_{Rt}}-r_{,_{R}}\lambda_ {,_{t}}\right)/r\,,\] (7) \[ 8\pi T^{\theta}_{\theta}=8\pi T^{\varphi}_{\varphi}=-q^{2}/r^{4} +\Lambda=-\left\{e^{-\lambda}\left[2r_{,_{RR}}-r_{,_{R}}\lambda_{,_{R}}\right] -2r_{,_{tt}}-r\lambda_{,_{tt}}-r\lambda_{,_{t}}^{2}/2-r_{,_{t}}\lambda_{,_{t}} \right\}/(2r)\,.\] (8) **Таким образом, энергетико-импульсный тензор включает три типа вещества: центрально-симметричное магнитное поле, космологический термин \(\Lambda\) и пылевидное вещество с плотностью⁵ \(\varepsilon\).** [FOOTNOTE:5][ENDFOOTNOTE] - [СНОСКА:5][КОНЕЦ СНОСКИ] ## 3 Решение и начальные условия Уравнение (7) может быть интегрировано относительно времени: \[\exp^{-\lambda}r^{2}_{,{R}}=F_{1}(R)\,.\] (9) На горле должно выполняться условие \({r_{,_{R}}=0}\), и поэтому \[F_{1}(0)=0\,.\] (10) \[F_{1}(0)=0\,.\] (10) Подставив (9) в уравнение (6), мы получаем \[\frac{q^{2}}{r^{2}}+\Lambda r^{2}=\left(rr^{2}_{,_{t}}\right)_{,t}/r_{,_{t}}-F _{1}+1\,.\] (11) 11) \[\frac{q^{2}}{r^{2}}+\Lambda r^{2}=\left(rr^{2}_{,_{t}}\right)_{,t}/r_{,_{t}}-F _{1}+1\,.\] Интегрируя это уравнение по времени, получим: \[\frac{q^{2}}{r}-\Lambda r^{3}/3+rr^{2}_{,_{t}}+(1-F_{1})r=F_{2}(R)\,.\] (12) \[\frac{q^{2}}{r}-\frac{\Lambda r^{3}}{3}+rr^{2}_{,_{t}}+(1-F_{1})r=F_{2}(R)\,.\] (12) Функции \({F_{1}(R)}\) и \({F_{2}(R)}\) определяют начальные условия для распределения скорости и плотности пыли. С выражением \({\lambda_{,_{t}}}\) и \({\lambda_{,_{tt}}}\) из равенства (7), уравнение (8) может быть переписано как \[\left[q^{2}/r^{2}+\Lambda r^{2}+e^{-\lambda}r_{,_{R}}^{2}-r_{,_{t}}^{2}-2rr_{, _{tt}}\right]_{,_{R}}=0\,.\] (13) \[\left[q^{2}/r^{2}+\Lambda r^{2}+e^{-\lambda}r_{,_{R}}^{2}-r_{,_{t}}^{2}-2rr_{, _{tt}}\right]_{,_{R}}=0\,.\] (13) Когда уравнение (6) удовлетворено, интегрирование уравнения (13) приводит к тождеству. **Это тождество является следствием установки компоненты времени в метрике (4) равной единице, что обосновывает этот выбор метрики.** С методологической точки зрения следует отметить, что эта форма метрики для пыли является очевидной, поскольку пыль не имеет давления, и, следовательно, наблюдательная система соприкасающегося пространства является синхронной. Однако это не так очевидно, когда вводится сферически симметричное электромагнитное поле, и полученная идентичность является следствием отсутствия взаимодействия между беззарядной пылью и электромагнитным полем. Более того, Лоренцево преобразование вдоль магнитных силовых линий не изменяет это поле, что обосновывает использование системы отсчета, связанной с движущейся пылью. Для движения в этой системе отсчета (вдоль поля) электромагнитное поле остается неизменным. Если бы метрика не могла быть представлена в форме (4), дальнейшие расчеты были бы невозможны. Именно это неочевидное обстоятельство позволило нам успешно разработать наш метод и получить все важные результаты. Умножая уравнение (5) на \({r^{2}r_{,_{R}}}\) и выражая \({\lambda_{,_{t}}}\) из уравнения (7), получаем \[8\pi\varepsilon r^{2}r_{,_{R}}+\left[\frac{\Lambda r^{3}}{3}-\frac{q^{2}}{r}-r(1-F_{1})-rr_{,_ {t}}^{2}\right]_{,_{R}}=0\,.\] (14) Интегрируя это по \(R\) от \(0\) до \(R\), с учетом (10), получаем \[ \int\limits_{0}^{R}8\pi\varepsilon r^{2}r_{,_{R}}\,dR-q^{2}/r+\Lambda r^{3}/3- r(1-F_{1})-rr_{,_{t}}^{2}=-q^{2}/r_{{}_{0}}+\Lambda r_{{}_{0}}^{3}/3-r_{{}_{0} }-r_{{}_{0}}r_{{}_{0},_{t}}^{2}\,. \] (15) Здесь мы учли, что функция \({r(R=0)=r_{{}_{0}}(t)}\) может зависеть от времени. Выражая \({rr_{,_{t}}^{2}}\) из (12) и подставляя его в (15), получаем \[\int\limits_{0}^{R}8\pi\varepsilon r^{2}r_{,_{R}}\,dR=F_{2}(R)-q^{2}/r_{{}_{0} }-r_{{}_{0}}+\Lambda r_{{}_{0}}^{3}/3-r_{{}_{0}}r_{{}_{0},_{t}}^{2}\,.\] (16) \[\int\limits_{0}^{R}8\pi\varepsilon r^{2}r_{,_{R}}\,dR=F_{2}(R)-q^{2}/r_{{}_{0} }-r_{{}_{0}}+\Lambda r_{{}_{0}}^{3}/3-r_{{}_{0}}r_{{}_{0},_{t}}^{2}\,.\] (16) Производная данного выражения по отношению к \(R\) дает еще один интеграл движения (который выражает сохранение массы в соприкасающемся объеме): \[8\pi\varepsilon r^{2}r_{,_{R}}=\frac{dF_{2}}{dR}\,,\] (17) Идентичности Бьянки⁶: [ССЫЛКА:6][КОНЕЦ_ССЫЛКИ] \[ T^{n}_{k;n}=\frac{1}{\sqrt{-g}}\,\frac{\partial(T^{n}_{k}\sqrt{-g})}{\partial x^{n}}-\frac{T^{nl}}{2}\,\frac{\partial g_{nl}}{\partial x^{k}}=0 \quad (18) \] содержатся в уравнениях Эйнштейна, их компоненты \({k=t, \theta, \varphi}\) равны нулю тождественно, и компонента \({k=R}\) дает результат в (17), который является аналогом интеграла для решения чисто пылевого решения (см. [31], \(\lx@sectionsign\)103) в теории эволюции облака пыли. Явный вид функции \({e^{\lambda}(R, t) = r_{,_{R}}^{2}/F_{1}}\) и неявный вид функции \({r^{2}(R, t)}\) получены в разделе 4. **Ниже мы используем индекс "i" для обозначения всех величин в начальный момент времени \({t=0}\).** Распределение скорости изначально установлено равным нулю. \[\left.r_{,_{t}}^{2}\right|_{(t=0)}=0\] (19) \[\left. r_{,_{t}}^{2}\right|_{(t=0)}=0 \] (19) В Приложении A рассматривается ненулевая начальная скорость. Мы отмечаем, что во всех случаях выбор начальных условий не является произвольным и должен удовлетворять ограничениям, наложенным (5) и (7). Эти уравнения не содержат вторых производных по времени и, как известно (см. [27]), при условии, что \({t={\rm\,const}}\) на начальном сечении, они автоматически удовлетворяются для всех значений \(t\) в силу других уравнений Эйнштейна. Мы выбираем начальный масштаб координат \(R\) в (4) таким образом, что \[r_{i}=\sqrt{q^{2}+R^{2}}\,,\qquad\varepsilon_{di}\equiv\varepsilon_{d}(r_{i})= -\frac{q^{2}}{4\pi r_{i}^{4}}\,.\] (20) \[r_{i}=\sqrt{q^{2}+R^{2}}\,,\qquad\varepsilon_{di}\equiv\varepsilon_{d}(r_{i})= -\frac{q^{2}}{4\pi r_{i}^{4}}\,.\] (20) где \({r_{i}(R)}\) совпадает с (1) и уравнение (10) автоматически удовлетворяется. Мы устанавливаем \[s(r_{i})\equiv\frac{1}{r_{i}}\int\limits_{0}^{R}8\pi(\varepsilon_{i}- \varepsilon_{di})r_{i}^{2}r_{i,_{R}}\,dR=\frac{1}{r_{i}}\int\limits_{q}^{r_{i} }8\pi\varepsilon_{i}r_{i}^{2}\,dr_{i}+2\frac{q}{r_{i}}\left(1-\frac{q}{r_{i}}\right)\] (21) \[s(r_{i})\equiv\frac{1}{r_{i}}\int\limits_{0}^{R}8\pi(\varepsilon_{i}- \varepsilon_{di})r_{i}^{2}r_{i,_{R}}\,dR=\frac{1}{r_{i}}\int\limits_{q}^{r_{i} }8\pi\varepsilon_{i}r_{i}^{2}\,dr_{i}+2\frac{q}{r_{i}}\left(1-\frac{q}{r_{i}}\right)\] (21) Количество \(s\) имеет значение удвоенного ньютоновского потенциала избыточной пылевой материи относительно \(\varepsilon_{d}\) [см. (20)]. Связь этого потенциала с функциями \(F_{1}\) и \(F_{2}\) следует из (15) и (16) в начальный момент времени: \[F_{1}=1-s-\frac{q^{2}}{r_{i}^{2}}-\frac{\Lambda}{3}\left(r_{i}^{2}-q^{3}/r_{i} \right)\,,\] (22) \[F_{1}=1-s-\frac{q^{2}}{r_{i}^{2}}-\frac{\Lambda}{3}\left(r_{i}^{2}-\frac{q^{3}}{r_{i}} \right)\,,\] (22) \[\begin{equation} F_{2}=r_{i}\left(s+2\frac{q^{2}}{r_{i}^{2}}-\frac{\Lambda q^{3}}{3r_{i}}\right ) \end{equation}\] (23) Уравнение (9) подразумевает, что \({F_{1}\geq 0}\). Согласно (22), это накладывает ограничения на распределение \({s(R)}\). Из уравнения (6) мы можем найти \({r_{,_{tt}}}\) в начальный момент: \[ \text{при } t=0\,:\quad r_{,_{tt}}=-\frac{s}{2r_{i}}+\frac{\Lambda r_{i}}{3}+ \frac{\Lambda q^{3}}{6r_{i}^{2}} \] (24) Уравнение (24) показывает, что при \({\Lambda=0}\) динамика отсутствует в области, где \({s=0}\) (по крайней мере до момента пересечения пылевых слоев, когда рассматриваемая модель становится неприменимой). ## 4 Решение без терма \(\Lambda\) Мы рассмотрим случай \({\Lambda=0}\) более подробно. For \({\Lambda=0}\), it follows from Eqn (24) that the WH throat size remains constant \({[r_{{}_{0}}(t)=q]}\) in the whole region of the allowed values of \(R\) and \(t\) for the sought solution, until matter starts flowing through the throat. In addition, expression (24) implies that the dynamics of matter in a WH depend only on the internal layers of matter (with smaller values of r) and are independent of the external layers. Therefore, matter on one side of the throat does not influence matter on the opposite side (unless there is matter flowing through the throat or layer intersection occurs). Для \({\Lambda=0}\) из уравнения (24) следует, что размер горла червоточины остается постоянным \({[r_{{}_{0}}(t)=q]}\) во всем промежутке допустимых значений \(R\) и \(t\) для искомого решения, пока через горло не начинает протекать материя. Кроме того, выражение (24) подразумевает, что динамика материи в червоточине зависит только от внутренних слоев материи (с меньшими значениями r) и не зависит от внешних слоев. Поэтому материя с одной стороны горла не оказывает влияния на материю с противоположной стороны (за исключением случаев, когда через горло протекает материя или происходит пересечение слоев). Это можно проверить непосредственно по формуле (24), что в начальный момент времени ускорение \({r_{,_{tt}}}\) является отрицательным при \({s>0}\). Следовательно, избыточная масса пыли должна коллапсировать. Мы вводим определение видимого горизонта. [ФИГУРА: S4.F1] [КОНЕЦФИГУРЫ] **Критерий отсутствия явного горизонта при коллапсе задается следующим образом:** \[V<1\] (25) \[V<1\] (25) для скорости пыли [см. также [23],[29],[30],[24] и (12)], где скорость пыли \(V\) определяется как \[V^{2}\equiv r_{,_{t}}^{2}e^{\lambda}/r_{,_{R}}^{2}=r_{,_{t}}^{2}/F_{1}=\frac{( s+2q^{2}/r_{i}^{2})r_{i}/r-s-q^{2}/r_{i}^{2}-q^{2}/r^{2}}{1-s-q^{2}/r_{i}^{2}}\] (26) \[\[V^{2}\equiv r_{,_{t}}^{2}e^{\lambda}/r_{,_{R}}^{2}=r_{,_{t}}^{2}/F_{1}=\frac{( s+2q^{2}/r_{i}^{2})r_{i}/r-s-q^{2}/r_{i}^{2}-q^{2}/r^{2}}{1-s-q^{2}/r_{i}^{2}}\]\] (26) Для \({q=0}\), этот результат совпадает с решением для коллапсирующей пыли (см. [23]). Чтобы избежать неопределенности \({0/0}\) для функции \(V^{2}\) в узком месте в начальный момент времени \({(F_{1}[r_{i}\to r_{{}_{0}}]\to 0)}\), необходимо обеспечить более быструю сходимость к нулю функции \({r_{,_{t}}^{2}(t=0,r_{i}\to r_{{}_{0}})}\) по сравнению с функцией \({F_{1}(r_{i}\to r_{{}_{0}})}\) (см. Приложение A). [FIGURE:S4.F2][ENDFIGURE] Закон движения слоя пыли может быть найден из (12): \[t=\int\limits_{r_{i}}^{r}\frac{-r\,dr}{\sqrt{(F_{1}-1)r^{2}+F_{2}r-q^{2}}}= \int\limits_{r_{i}}^{r}\frac{-r\,dr}{r_{i}\sqrt{(1-r/r_{i})[(s+q^{2}/r_{i}^{2} )r/r_{i}-q^{2}/r_{i}^{2}]}}\] (27) \[т=\int\limits_{r_{и}}^{р}\frac{-р\,др}{\sqrt{(F_{1}-1)р^{2}+F_{2}р-q^{2}}}= \int\limits_{r_{и}}^{р}\frac{-р\,др}{r_{и}\sqrt{(1-р/r_{и})[(s+q^{2}/r_{и}^{2} )р/r_{и}-q^{2}/r_{и}^{2}]}}\] (27) Эта квадратура может быть интегрирована элементарно: \[t=r_{i}\frac{\sqrt{(1-r/r_{i})[(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}]}}{s +q^{2}/r_{i}^{2}}+r_{i}\frac{s+2q^{2}/r_{i}^{2}}{2(s+q^{2}/r_{i}^{2})^{3/2}} \cdot\arccos\left[1-\frac{2(s+q^{2}/r_{i}^{2})(1-r/r_{i})}{s}\right]\] (28) или в другой форме \[t=r_{i}\left[\frac{\sqrt{(1-r/r_{i})[(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2 }]}}{s+q^{2}/r_{i}^{2}}+\frac{s+2q^{2}/r_{i}^{2}}{(s+q^{2}/r_{i}^{2})^{3/2}} \cdot{\rm\,arctg}\sqrt{\frac{(s+q^{2}/r_{i}^{2})(1-r/r_{i})}{(s+q^{2}/r_{i}^{2 })r/r_{i}-q^{2}/r_{i}^{2}}}\right]\] (29) Таким образом, движение слоев пыли зависит от избыточного потенциала \(s\) и начального расстояния от глотки черной дыры: \(r_{i}/q\). Однако эту модель можно считать физически правильной только до возможного пересечения слоев пыли. Это связано с тем, что после пересечения в материальной системе появляется входящий поток энергии (из пересекающихся слоев вещества), который не учитывается в тензоре энергии-импульса. Пересечение смежных слоев вещества соответствует бесконечной плотности энергии. Это соответствует условию \({r_{,_{R}}=0}\) (или \({\frac{dr}{dr_{i}}=0}\)) [см. (20)]. Дифференцирование (29) по отношению к \({r_{i}}\) позволяет явно определить функцию \({\frac{dr}{dr_{i}}(r,s,q)}\). Дифференцирование левой части (29) даёт ноль. Мы обозначим производную по отношению к \(r_{i}\) символом штрих, выразим все расстояния в единицах \(r_{i}\) и опустим промежуточные громоздкие вычисления; окончательное выражение для этой функции представлено \[r^{\prime}=1+\frac{(1-r)\left[s(s^{\prime}-2q^{2})(2q^{2}-r\{s+q ^{2}\})-q^{2}(s+2q^{2})(2s^{\prime}+s)\right]}{2rs(s+q^{2})^{2}}+\] \[+\frac{\left[2s(s+q^{2})+(2q^{2}-s^{\prime})(s+4q^{2})\right] \sqrt{(1-r)[(s+q^{2})r-q^{2}]}}{2r(s+q^{2})^{5/2}}\cdot{\rm\,arctg}\sqrt{\frac {(s+q^{2})(1-r)}{(s+q^{2})r-q^{2}}}\] (30) Невозможно использовать эту формулу для определения момента пересечения непримыкающих слоев, потому что пересечение с непримыкающими слоями не приводит к никаким нерегулярностям для пыли. Очевидно, пересечение непримыкающих слоев происходит после пересечения смежных и не может распространяться со сверхсветовой скоростью. Поэтому, после построения диаграмм \(t(r_{i})\) для световых конусов и кривой, соответствующей пересечению смежных слоев \({(r^{\prime}=0)}\), мы можем определить области, которые определенно не содержат пересечений слоев (см. Рисунок 1 или 2). Используя формулу (26), мы можем сделать несколько важных выводов. **1. Образование горизонта возможно только при достаточно большом параметре \(s\):** \[\(s>2\frac{q}{r_{i}}\left(1-\frac{q}{r_{i}}\right)\) (31)\] **После появления горизонта следует, что Черная Дыра становится "непроходимой".** Однако слои пыли могут уже начать пересекаться, прежде чем горизонт будет достигнут. **2. Значения функции \({t(r,r_{i})}\) ограничены максимальным временем \(t_{stop}\) (от начала движения до остановки).** В (28) это время соответствует аргументу функции \({\bf\arccos}\), равному минус единице (или нулевому значению выражения в квадратном корне в той же формуле): \[t_{stop}=\frac{\pi r_{i}(s+2q^{2}/r_{i}^{2})}{2(s+q^{2}/r_{i}^{2})^{3/2}}\] (32) \[t_{остановка}=\frac{\pi r_{вх}(s+2q^{2}/r_{вх}^{2})}{2(s+q^{2}/r_{вх}^{2})^{3/2}}\] (32) Время \(t_{stop}\) соответствует отклонению \({\Delta r\approx sr_{i}^{3}/q^{2}}\) от начального положения. **Для малых отклонений (соответствующих малым значениям \(s\)), происходят гармонические колебания с периодом \({T=2t_{stop}\approx 2\pi r_{i}^{2}/q}\)** (см. Приложение B). **3. Существование второго (меньшего) корня уравнения \({V^{2}(r)=1}\) означает появление второго (внутреннего) горизонта в системе (см. рисунки 1 и 2).** 4. Для параметра \({s=2q(1-q/r_{i})/r_{i}}\) (или \({\varepsilon=0}\)) скаляр \({\bf g^{ik}\,r_{;i}r_{;k}=(1-q/r)^{2}}\) (скаляр, равный скаляру экстремального решения Райснера-Нордстрёма). Следовательно: **если плотность энергии стремится к нулю - решение (29) стремится к экстремальному решению Райснера-Нордстрёма черной дыры (в сопровождающей, свободно падающей системе отсчёта).** ## 5 Решение для \(s=0\) с \(\Lambda\)-термом Мы рассматриваем случай, когда \(s=0\). Уравнение (6) с (9) и (22) тогда принимает вид \[2rr_{,_{tt}}=\Lambda r^{2}+q^{2}\left(\frac{1}{r^{2}}-\frac{1}{r_{i}^{2}} \right)-\frac{\Lambda}{3}\left(r_{i}^{2}-q^{3}/r_{i}\right)-r^{2}_{,_{t}}\,,\] (33) \[2rr_{,_{tt}}=\Lambda r^{2}+q^{2}\left(\frac{1}{r^{2}}-\frac{1}{r_{i}^{2}} \right)-\frac{\Lambda}{3}\left(r_{i}^{2}-\frac{q^{3}}{r_{i}}\right)-r^{2}_{,_{t}}\,,\] (33) и уравнение (12) принимает вид \[r^{2}_{,_{t}}=(r-r_{i})\left[-\frac{q^{2}}{r^{2}r_{i}^{2}}(r-r_{i})+\frac{ \Lambda}{3}\left(r+r_{i}+\frac{q^{3}}{rr_{i}}\right)\right]\,.\] (34) \[r^{2}_{,_{t}}=(r-r_{i})\left[-\frac{q^{2}}{r^{2}r_{i}^{2}}(r-r_{i})+\frac{ \Lambda}{3}\left(r+r_{i}+\frac{q^{3}}{rr_{i}}\right)\right]\,.\] (34) officially known as the cosmological constant \(s\) is equal to zero, it implies that matter begins expanding from a state of rest (as indicated in equation 19), which is caused by the inflation due to the cosmological constant \(\Lambda\). \[a\equiv\Lambda q^{2}\] (35) \[a\equiv\Lambda q^{2}\] (35) **превышает некоторое критическое значение \({a_{cr}}\), инфляция продолжается неограниченно во всем объеме \({(q\leq r_{i}\leq r<\infty)}\) до образования внешнего горизонта, \({V^{2}(r)=1}\)}.** Значение \({a_{cr}}\) определяется из условия максимума выражения для параметра \(a\), которое получается, приравнивая второй множитель (в квадратных скобках) в уравнении (34) к нулю: \[a_{cr}=MAX\left[\frac{3\tilde{q}^{4}(1-\tilde{r})\tilde{r}^{2}}{1+\tilde{r}+ \tilde{r}^{2}\tilde{q}^{3}}\right]\approx 0.22\,,\quad\tilde{r}\equiv r_{i}/r \,,\quad\tilde{q}\equiv q/r_{i}\,.\] (36) \[a_{cr}=MAX\left[\frac{3\tilde{q}^{4}(1-\tilde{r})\tilde{r}^{2}}{1+\tilde{r}+ \tilde{r}^{2}\tilde{q}^{3}}\right]\approx 0.22\,,\quad\tilde{r}\equiv r_{i}/r \,,\quad\tilde{q}\equiv q/r_{i}\,.\] (36) **Для \({a<a_{cr}}\), появляется регион, где инфляция останавливается.** Этот регион начинает возникать у горла и расширяется в сторону больших значений \(r_{i}\) при уменьшении параметра \(a\). **При \({r/r_{i}\to\infty}\), инфляция происходит экспоненциально: \({r\propto\exp(t\sqrt{\Lambda/3})}\).** Функцию \(r^{\prime}\) можно выразить в квадратурах (см. Приложение C): \[r^{\prime}=1+\sqrt{r-r_{i}}\exp\left(-\int\limits_{r_{i}}^{r}P_{ 2}(x)\,dx\right)\cdot\int\limits_{r_{i}}^{r}\frac{Q_{2}(r)-P_{2}(r)}{\sqrt{r-r _{i}}}\exp\left(\int\limits_{r_{i}}^{r}P_{2}(x)\,dx\right)\,dr\,,\] \[P_{2}=\frac{\frac{r_{i}^{2}}{2r^{2}}-\frac{r_{i}^{2}(r-r_{i})}{r ^{3}}-\frac{a}{2}\left(1-\frac{q^{3}}{r^{2}r_{i}}\right)}{-\frac{r_{i}^{2}(r-r _{i})}{r^{2}}+a\left(r+r_{i}+\frac{q^{3}}{rr_{i}}\right)}\,,\quad Q_{2}-P_{2}= \frac{a+(r+r_{i})\left(\frac{r_{i}(r-r_{i})}{r^{3}}-\frac{aq^{3}}{2r^{2}r_{i}^ {2}}\right)}{-\frac{r_{i}^{2}(r-r_{i})}{r^{2}}+a\left(r+r_{i}+\frac{q^{3}}{rr_ {i}}\right)}\,.\] (37) Используя эту уравнение, мы можем найти области, где происходит инфляция без пересечений пылевого слоя. ## 6 Модель Мультивселенной Пыль с положительным \(s\) изначально ускоряется к центру (без термина \(\Lambda\)). Терм \(\Lambda\) без избыточной пыли приводит к исходному инфляционному решению [см. (24)]. В горловине червоточины потенциал \(s=0\), а терм \(\Lambda\) в горловине обеспечивает ненулевое ускорение материи. Этот вклад не может быть скомпенсирован в или около горловины [см. (6)], где \({r_{,_{t}}=r_{,_{tt}}=0}\) и \({r=q}\). Следовательно, для червоточины с радиусом горловины \({r_{{}_{0}}=q}\) и термом \(\Lambda\) не существует статического решения. Тем не менее, статическое решение существует для WH с термином \(\Lambda\) и \({r_{{}_{0}}\neq q}\). Это решение легко вывести из уравнений (5), (6) и (8) (с \({r_{,_{t}}=0}\) и \({r_{,_{tt}}=0}\)). Метрика статического БГ определяется выражением (1), с учетом того, что \({r^{2}(R)\neq q^{2}+R^{2}}\). Из (6) получаем \({r_{,_{R}}^{2}=1-q^{2}/r^{2}-\Lambda r^{2}}\) и легко находим выражение для радиуса глотки \({r_{{}_{0}}}\), \[\Lambda r_{{}_{0}}^{4}-r_{{}_{0}}^{2}+q^{2}=0\quad\Rightarrow\quad r_{{}_{0}}^ {2}=\frac{1-\sqrt{1-4\Lambda q^{2}}}{2\Lambda}\to q^{2}(1+\Lambda q^{2})\qquad (\text{at }\Lambda q^{2}\to 0)\,,\] (38) и зависимость \({r(R)}\): \[r^{2}(R)=\frac{1-\sqrt{1-4\Lambda q^{2}}\cdot\cos(2\sqrt{\Lambda}R)}{2\Lambda}\] (39) Распределение \(\varepsilon\) для этого решения определяется⁷ из уравнения (5): [FOOTNOTE:7][ENDFOOTNOTE] - [СНОСКА:7][КОНЕЦСНОСКИ] \[\varepsilon=\frac{\Lambda}{4\pi}-\frac{q^{2}}{4\pi r^{4}}\] (40) Таким образом, для статического решения с термином \(\Lambda\), радиус горла и плотность пыли больше, чем без термина \(\Lambda\). Общая плотность энергии для статического решения с термом \(\Lambda\) равна \[T^{t}_{t}=\frac{3\Lambda}{8\pi}-\frac{q^{2}}{8\pi r^{4}}\] (41) (41) \[T^{t}_{t}=\frac{3\Lambda}{8\pi}-\frac{q^{2}}{8\pi r^{4}}\] Условие того, что значение \({T^{t}_{t}}\) будет неотрицательным везде в пространстве (для \({r\geq r_{{}_{0}}}\)), имеет вид \[\[T^{t}_{t}\geq 0\quad\makebox{at }a=\Lambda q^{2}\geq\frac{3}{16}\] (42)\] => \[T^{t}_{t}\geq 0\quad\makebox{при }a=\Lambda q^{2}\geq\frac{3}{16}\] (42)\] **Следовательно, в присутствии термина \(\Lambda\), можно найти решения червоточин с положительной общей плотностью энергии.** Из (39) мы можем получить максимально допустимый радиус статической метрики с термом \(\Lambda\): \[r_{\text{max}}^{2}=\frac{1+\sqrt{1-4\Lambda q^{2}}}{2\Lambda}\to\frac{1}{\Lambda} \qquad(\text{при }\Lambda q^{2}\to 0)\,.\] (43) После этого радиуса Вселенная начинает сжиматься снова, пока не произойдёт новое горло. **Решение (39) описывает статический Мультивселенную с бесконечным числом горловин. Когда нет заряда \({(q=0)}\), это решение становится космологическим решением без червоточин, соответствующим закрытой изотропной Вселенной** (см. §112, [31]). Когда имеется избыток (или дефицит) энергетической плотности пыли или термина Лямбда относительно (40), полученное решение для Мультивселенной становится динамическим. Его аналитическое исследование осложнено необходимостью решения алгебраического уравнения четвёртого порядка и вычисления квадратуры, аналогичной (37), для момента пересечения пылевого слоя. ## 7 Заключение В данной статье мы обобщили и развили ранее предложенный метод из работ [20], [22] и применили его к новым проблемам в современной космологии. Мы нашли и проанализировали аналитические решения уравнений общей теории относительности, описывающих динамику проходимого червоточины. Полученные результаты важны для анализа общих свойств проходимых червоточин. Мы также получили решение, описывающее сферически-симметричную модель Мультивселенной. Мы не анализировали свойства геодезических, описывающих движение частиц и других веществ (энергии и информации) через червоточину и ее окрестности. Эти проблемы, которые в основном важны для анализа возможного наблюдаемого вида подобных объектов, рассматриваются в другом месте (см., например, [11]). Чтобы заключить, мы замечаем о термине "Многомерная Вселенная". Этот термин используется в физике и космологии в двух разных смыслах. Во-первых, этот термин предполагает возможность параллельного существования множества или даже бесконечного количества различных миров, возможно возникших из квантового вакуума (в некотором смысле, в разных местах и в разное время). В данной статье этот термин используется именно в этом смысле. Во-вторых, этот термин иногда используется для обозначения выборки различных реальностей в интерпретации Эверетта квантовой механики. Использование одного термина для разных понятий иногда является неоднозначным. По нашему мнению, для этих концепций следует использовать разные термины. Мы предлагаем сохранить термин "Мультивселенная" для космологии и обозначить множество миров Эверетта (следуя предложению М.Б. Менски) как "Альтервселенная", помня о различных классических альтернативах мира Эверетта. ## 8 Благодарности Мы благодарны сотрудникам отдела теоретической астрофизики Физического института имени Лебедева за обсуждения. Работа поддерживается грантами Российского фонда фундаментальных исследований \(07-02-01128a\) и \(08-02-00090a\), грантами научных школ \(NSh-626.2008.2\) и \(NSh-2469.2008.2\), а также программой Российской академии наук "Происхождение и эволюция звезд и галактик 2008". ## Приложение А Начальные условия с ненулевой скоростью У горла ВХ, выражение для \(V^{2}\) в (26) включает неоднозначность \({0/0}\). Чтобы разрешить эту неоднозначность, мы рассматриваем модель с ненулевой начальной скоростью вещества. Вводим обозначения \[1-q/r_{i}\equiv\alpha\,,\quad r_{i}/r-1\equiv\beta\,,\quad\left.r_{,_{t}}^{2} \right|_{(t=0)}\equiv\gamma\,.\] (44) \[1-q/r_{i}\equiv\alpha\,,\quad r_{i}/r-1\equiv\beta\,,\quad\left.r_{,_{t}}^{2} \right|_{(t=0)}\equiv\gamma\,.\] (44) и предположим, что \({\Lambda=0}\). Выражения для функций \(F_{1}\) и \(F_{2}\) с \({\gamma\neq 0}\) [см. (15) и (12)] представлены следующим образом \[ F_{1}=1-s-q^{2}/r_{i}^{2}+\gamma-\gamma_{{}_{0}}q/r_{i}\,,\quad F_{2}=r_{i} \left[s+2q^{2}/r_{i}^{2}+\gamma_{{}_{0}}q/r_{i}\right]\,.\] (45) \] (45) С учетом (12) и ненулевой начальной скорости, выражение для \(V^{2}\) в (26) принимает форму \[ V^{2}=\frac{-s-q^{2}/r_{i}^{2}+\gamma-\gamma_{{}_{0}}q/r_{i}+(s+2q^{2}/r_{i}^{ 2}+\gamma_{{}_{0}}q/r_{i})r_{i}/r-q^{2}/r^{2}}{1-s-q^{2}/r_{i}^{2}+\gamma- \gamma_{{}_{0}}q/r_{i}}\] (46) \] \[ V^{2}=\frac{-с-к^{2}/р_{и}^{2}+\гамма-\гамма_{{}_{0}}к/р_{и}+(с+2к^{2}/р_{и}^{ 2}+\гамма_{{}_{0}}к/р_{и})р_{и}/р-к^{2}/р^{2}}{1-с-к^{2}/р_{и}^{2}+\гамма- \гамма_{{}_{0}}к/р_{и}}\] (46) Вблизи горла вблизи начального мгновения, функции \(\alpha\) и \(\beta\) принимают малые значения. Из (21), в линейном порядке по \(\alpha\) имеем: \[s\approx\alpha\kappa\,,\quad\kappa=8\pi r_{i}^{2}(\varepsilon_{i}-\varepsilon_{d})\approx 8\pi\varepsilon_{{}_{0}}q^{2}+2<2\,.\] \[s \approx \alpha\kappa\,,\quad\kappa=8\pi r_{i}^{2}(\varepsilon_{i}-\varepsilon_{d})\approx 8\pi\varepsilon_{{}_{0}}q^{2}+2<2\,.\] Мы рассматриваем уравнение (46) в линейном порядке по \(\alpha\) и \(\beta\). После всех преобразований мы в конечном итоге получаем \[V^{2}\approx\frac{\gamma+\gamma_{{}_{0}}\beta}{\gamma-\gamma_{{}_{0}}(1-\alpha )+\alpha(2-\kappa)}\to\frac{\gamma_{{}_{0}}(1+\beta)}{\alpha(\gamma_{{}_{0}}+2 -\kappa)}\text{ при }\gamma\to\gamma_{{}_{0}}\,(47)\] Из этого следует, что условие невырожденности \(V^{2}\) при горловине равно \({\gamma_{{}_{0}}=0}\). Затем \[V^{2}\approx\frac{\gamma}{\gamma+\alpha(2-\kappa)}\] (48) \[V^{2}\approx\frac{\gamma}{\gamma+\alpha(2-\kappa)}\] (48) Выражение (48) для \(V^{2}\) является регулярным и не имеет неоднозначностей, если функция \(\gamma\) стремится к нулю в горле быстрее, чем функция \(\alpha\). В этом случае скорость изменения радиуса \(r\) обращается в ноль в горле (как должно быть по определению горла). В линейном порядке по \(\beta\) функция \(V^{2}\) является неизменной во времени около горла. ## Приложение Б Исследование пересечений смежных слоев Мы рассматриваем модель без терма \(\Lambda\) для \(s>0\). В этом случае избыточное вещество коллапсирует, то есть \({r\leq r_{i}}\). **Лемма. Всегда существует ненулевой временной интервал \(\{0,t\}\), внутри которого нет пересечений смежных слоев.** Уравнение (30) подразумевает, что это очевидно для ненулевого потенциала \({s}\). Единственная точка, в которой это утверждение должно быть доказано, - точка, соответствующая \({s=0}\). Мы более подробно изучаем асимптотический режим \({s\to 0}\): \[s << \frac{q^{2}}{r_{i}^{2}} \leq 1\] (49) Из допустимого диапазона радиусов (до точки остановки) \({r\geq q^{2}/(sr_{i}+q^{2}/r_{i})}\), мы делаем вывод \[1-\frac{r}{r_{i}}\leq\frac{s}{s+q^{2}/r_{i}^{2}}\leq\frac{s}{q^{2}/r_{i}^{2}}<<1\] (50) \[1-\frac{r}{r_{i}}\leq\frac{s}{s+q^{2}/r_{i}^{2}}\leq\frac{s}{q^{2}/r_{i}^{2}}<<1\] (50) Поскольку последний член в (30) не содержит \(s\) в знаменателе, его можно пренебречь по сравнению с предыдущим членом. Это можно доказать более подробно, рассмотрев общий случай для отношения числителя и знаменателя в выражении квадратного корня для \({\bf\arctan}\): 1. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})<<(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) \( {(s+q^{2}/r_{i}^{2})(1-r/r_{i})<<(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) 2. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})\sim(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) 2. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})\approx(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) 3. \({(s+q^{2}/r_{i}^{2})(1-r/r_{i})>>(s+q^{2}/r_{i}^{2})r/r_{i}-q^{2}/r_{i}^{2}}\) 3. \({(s+\frac{q^{2}}{{r_{i}}^{2}})(1-\frac{r}{{r_{i}}})>>(s+\frac{q^{2}}{{r_{i}}^{2}})\frac{r}{{r_{i}}}-\frac{q^{2}}{{r_{i}}^{2}}}\) Сохраняя ведущие члены, мы получаем асимптотическую форму уравнения (30): \[ r^{\prime}\to 1+\frac{(1-r/r_{i})[-q^{2}\cdot 2q^{2}\cdot 2r_{i}s^{\prime}]}{2 sq^{4}}=1-2r_{i}s^{\prime}(1-r/r_{i})/s \quad (51) \] В аналогичном случае первый член в правой части выражения (28) может быть пренебрежен (по сравнению со вторым членом), и следовательно, асимптотически по отношению к времени мы имеем \[\cos\left(\frac{tq}{r_{i}^{2}}\right)\to 1-\frac{2q^{2}}{sr_{i}^{2}}(1-r/r_{i} )\quad\Longrightarrow\quad r\to r_{i}+\frac{sr_{i}^{3}}{2q^{2}}\left[\cos\left (\frac{tq}{r_{i}^{2}}\right)-1\right]\] (52) \[\cos\left(\frac{tq}{r_{i}^{2}}\right)\to 1-\frac{2q^{2}}{sr_{i}^{2}}(1-r/r_{i} )\quad\Longrightarrow\quad r\to r_{i}+\frac{sr_{i}^{3}}{2q^{2}}\left[\cos\left (\frac{tq}{r_{i}^{2}}\right)-1\right]\] (52) Сравнивая уравнения (51) и (52), мы получаем искомую асимптотическую форму при \({s\to 0}\): \[r^{\prime}\to 1-\frac{2r_{i}^{3}s^{\prime}}{q^{2}}\sin^{2}\left(\frac{tq}{2r_{ i}^{2}}\right).\] (53) is translated to: \[r^{\prime}\to 1-\frac{2r_{i}^{3}s^{\prime}}{q^{2}}\sin^{2}\left(\frac{tq}{2r_{ i}^{2}}\right).\] (53) Это доказывает лемму. Кроме того, уравнение (52) подразумевает гармоническую динамику (колебания) для \({s\to 0}\) и \({2r_{i}^{3}s^{\prime}/q^{2}<1}\). ## Приложение C Квадратура для \(r^{\prime}\) в решении с \(\Lambda\)-термом Мы дифференцируем \(r_{,_{t}}^{2}\) по отношению к \(r_{i}\): \[\frac{dr_{{,_{t}}}^{2}}{dr_{i}}=2r_{{,_{t}}}r^{{\prime}}_{{,_{t}}}=2r_{{,_{t}}}^{2}\frac{dr^{{\prime}}}{dr}\quad\Rightarrow\quad\frac{dr^{{\prime}}}{dr}=\frac{1}{2r_{{,_{t}}}^{2}}\cdot\frac{dr_{{,_{t}}}^{2}}{dr_{i}}\] (54) Подставляя уравнение (34) в (54) и дифференцируя его по отношению к \(r_{i}\), мы получим следующее уравнение для функции \({y(r)\equiv r^{\prime}}\): \[\frac{dy}{dr}+P(r)y=Q(r)\,,\] (55) \[\frac{dу}{др}+P(r)y=Q(r)\,,\] (55) Здесь функции \({ P(r)\equiv P_{1}(r)+P_{2}(r) }\) и \({ Q(r)\equiv Q_{1}(r)+Q_{2}(r) }\) заданы следующим образом (для удобства, ниже предполагается, что \(r_{i}\) равно единице): \[P_{1}=\frac{-1}{2(r-1)}\,,\quad P_{2}=\frac{1/(2r^{2})-(r-1)/r^{ 3}-(a/2)(1-q^{3}/r^{2})}{(1-r)/r^{2}+a(1+r+q^{3}/r)}\,,\] \[Q_{1}=\frac{-1}{2(r-1)}\,,\quad Q_{2}=\frac{1/(2r^{2})+(r-1)/r^{ 2}+(a/2)(1-q^{3}/r)}{(1-r)/r^{2}+a(1+r+q^{3}/r)}\,.\] (56) Уравнение (55) имеет стандартное решение. \[y(r)=\exp\left[-\int\limits_{r_{1}}^{r}P(x)\,dx\right]\cdot\left\{\int\limits_ {r_{2}}^{r}Q(r)\cdot\exp\left[+\int\limits_{r_{1}}^{r}P(x)\,dx\right]\,dr+C_{1 }\right\}\] (57) Константы \(C_{1}\), \(r_{1}\) и \(r_{2}\) определяются начальными условиями. Экспонента может быть переписана следующим образом (первый член с \(P_{1}\) интегрируется): \[\exp\left[\int\limits_{r_{1}}^{r}P(x)\,dx\right]=\frac{C_{2}}{\sqrt{r-1}}\cdot \exp\left[\int\limits_{1}^{r}P_{2}(x)\,dx\right]\] (58) \[\exp\left[\int\limits_{r_{1}}^{r}P(x)\,dx\right]=\frac{C_{2}}{\sqrt{r-1}}\cdot \exp\left[\int\limits_{1}^{r}P_{2}(x)\,dx\right]\] (58) После этого, часть интеграла (57), соответствующая \(Q_1\), также может быть проинтегрирована (методом интегрирования по частям), с результатом \[y(r)=\sqrt{r-1}\cdot\exp\left[-\int\limits_{1}^{r}P_{2}(x)\,dx \right]\cdot\left\{\frac{1}{\sqrt{r-1}}\cdot\exp\left[+\int\limits_{1}^{r}P_{2 }(x)\,dx\right]\right|_{r_{2}}^{r}-\] \[\left.-\int\limits_{r_{2}}^{r}\frac{P_{2}(r)}{\sqrt{r-1}}\cdot \exp\left[+\int\limits_{1}^{r}P_{2}(x)\,dx\right]\,dr+\int\limits_{r_{2}}^{r} \frac{Q_{2}(r)}{\sqrt{r-1}}\cdot\exp\left[+\int\limits_{1}^{r}P_{2}(x)\,dx \right]\,dr+C_{1}\right\}\] (59) Затем мы можем переопределить нижний предел интегрирования и определить константу \(C_{1}\) из начальных условий. Конечное выражение для функции \({y(r)=r^{\prime}}\) представлено в уравнении (37). ## Ссылки * [1] С.В. Хокинг, _Черные дыры и структура Вселенной_, ред. К. Тейтелбоим и Дж. Занелли (World Sci., Сингапур, 2000), стр.23. * [2] Ф.С. Лобо, Phys.Rev., **D71**, 084011, (2005) * [3] Х. Шинкай, С.А. Хэйуорд, Phys.Rev., **D66**, 044005, (2002) * [4] М.С. Моррис, К.С. Том, Am. J. Phys., **56**, 395, (1988) * [5] Новиков И.Д., Ж. Эксп. Теор. Физ., **95**, 769, (1989) [Сов. Физ. ЖЭТФ 68 439 (1989)] * [6] И.Д. Новиков, Phys.Rev. **D45**, 1989, (1992) * [7] С.В. Хокинг, Phys.Rev., **D46**, 603, (1992) * [8] М. Виссер, _Лорентцевы червоточины: от Эйнштейна до Хокинга_, (Woodbury, NY: AIP, 1995) * [9] Шатский А., Астрон. Ж., **81**, 579, (2004) [Астрон. Репорт. 48 525 (2004)] * [10] Шатский А., Астрон. Ж., **84**, 99, (2007) [Астрон. Репорт. 51 81 (2007)] * [11] Кардашев Н.С., Новиков И.Д., Шатский А., Астрон. Ж., **83**, 675, (2006) [Астрон. Репорт. 50 601 (2006)] * [12] Н.С. Кардашев, И.Д. Новиков, А. Шатский, Int. J. Mod. Phys **D16**, 909, (2007) * [13] И.Д. Новиков, Н.С. Кардашев, Шатский А., Усп. Физ. Наук, **177**, 1017, (2007) [Физ. Усп. 50 965 (2007)] * [14] Черепащук А.М., Вестн. Моск. Гос. Ун-та, Сер. 3, Физ. Астрон. **(2)**, 62, (2005) [Моск. Ун-т Физ. Вестн. 60 (2) 74 (2005)] * [15] Бронников К.А, Старобинский А.А., Письма Ж. Эксп. Теор. Физ., **85**, 3, (2007) [JETP Lett. 85 1 (2007)]; gr-qc/0612032 * [16] В.П. Фролов, И.Д. Новиков, _Физика черных дыр. Основные концепции и новые разработки_, Kluver AP, (1998) * [17] А. Армендарис-Пикон, gr-qc/0201027, (2002) * [18] Б. Карр, редактор, _Вселенная или Мультивселенная?_, Cambridge Univ. Press, (2007) * [19] Х.Г.Эллис, J. Math. Phys., **14**, 104, (1973) * [20] Р. С. Толман, Proc. Nat. Acad. Sci. US, **20**, 169, (1934) * [21] Дж. Р. Оппенгеймер, Г. Снайдер, Phys. Rev., **56**, 455, (1939) * [22] Р. Сайбал, Д. Басанти, Р. Фарук и др., Int. J. Mod. Phys, **D16**, No11, стр.1745-1759, (2007) * [23] Шатский А., Андреев А.Ю., Ж. Эксп. Теор. Физ., **116**, 353, (1999) [JETP 89 189 [1999)] * [24] Шатский А., Ж. Эксп. Теор. Физ., **131**, 851, (2007) [JETP 104 743 (2007)] * [25] Шатский А., Новиков И.Д., Кардашев Н.С., Письма в Журнал экспериментальной и теоретической физики, **51**, (5) стр. 457-464, (2008) * [26] И. Фишер, _Скалярное мезостатическое поле с учетом гравитационных эффектов_, Журнал Экспериментальной Теоретической, **18**, 636, (1948) * [27] А. Янис, Э. Ньюман, Дж. Виникур, _Реальность Свартцильда Сингулярности_, Phys. Rev. Lett., **20**, 878, (1968) * [28] М. Вайман, _Статические сферически симметричные скалярные поля в общей теории относительности_, Phys. Rev. **D24**, 839, (1981) * [29] Новиков И.Д., Вестник Моск. Гос. Ун-та, Сер. 3, Физ. Астрон., **6**, стр.61, (1962) * [30] Зельдович Я.Б., Новиков И.Д., _Релятивистская Астрофизика_, Москва: Наука, (1967) [Перевод на английский: Relativistic Astrophysics Vol. 1 Stars and Relativity (Чикаго: Университет Чикаго Пресс, 1971)] * [31] Ландау Л.Д., Лифшиц Е.М., Теория Поля, _Классическая теория полей_, Москва: Наука, (1988) [Перевод на английский (Оксфорд: Издательство Пергамон, 1983)] Переведите маркдаун с английского на русский. Сохраните формулы : ``` Это *курсив* и это **жирный**. # Заголовок 1 ## Заголовок 2 ### Заголовок 3 - список - элемент 1. Нумерованный 2. список 3. элементов [ссылка](https://www.example.com)  `встроенный код` ``` блочный код ``` > Цитата Горизонтальная линия: --- Таблица: | Заголовок 1 | Заголовок 2 | | --- | --- | | Содержимое 1 | Содержимое 2 | Формула: $F = ma$ Формула в отдельной строке: $$ F = ma $$ ```

# Properties of Black Hole Radiation from Tunnelling Timothy Clifton _Department of Astrophysics, University of Oxford, Oxford OX1 3RH, UK_ e-mail: [email protected] (February 11, 2024) ###### Abstract We consider the space-time associated with the evaporation of a black hole by quantum mechanical tunnelling events. It is shown that the surface through which tunnelling occurs is distinct from the global event horizon, and that this has consequences for the radiation reaching future null infinity. A spherical collapse process is modelled, and the radiation expected to be observed at future null infinity is calculated. It is shown that external observers witness an evaporation process that begins as the tunnelling surface is exposed, and ends as the collapsing object passes behind its event horizon. The sensitivity of emitted radiation to the collapse process is illustrated. ## 1 Introduction A common interpretation of Hawking radiation [1] is that of virtual particles tunnelling through the horizon. In this picture a virtual pair is nucleated just inside (or just outside) the horizon. A quantum mechanical event then transports the positive energy particle from inside the horizon to the outside (or the negative energy particle from outside to inside). The result is a real particle materialising outside the black hole, and the mass of the hole being reduced. This long considered heuristic explanation of Hawking radiation was recently given a solid basis by Parikh and Wilczek [2]. The calculation they performed took into account the changing geometry of the space-time as the tunnelling events occur, and provides a natural time coordinate with which to parameterise the mass loss of the hole, as well as giving the location of the origin of radiation. Interestingly, it was shown that the spectrum of emitted radiation is not a precise black-body, as had previously been shown in [3], although it was not made clear how this could be linked to the collapse process that formed the hole. Here we consider a collapse process leading to the formation and subsequent evaporation of a black hole. We model this as a collapsing spherical shell of matter. Once formed, the hole is assumed to decrease in mass by the tunnelling process described above. The resulting geometry (as previously considered by Brown and Lindesay [4, 5, 6]) exhibits a global event horizon that is displaced from the origin of the radiation. The energy-momentum of the escaping radiation is then calculated. It is found, as expected, that an asymptotic observer watching the collapse witnesses an increase in the flux of radiation as he/she is exposed to the surface through which tunnelling occurs. This appears to the external observer as if radiation is being emitted before the collapsing object passes its own event horizon. The flux of radiation then continues to increase until the event horizon is reached. Similar results, by an alternative method, have been found in [7]. It is of interest to determine the sensitivity of the emitted radiation to the collapse process that forms the black hole. As is well known, all information about the collapse is removed in the limit that the event horizon is approached. Only the early radiation is sensitive to it [8]. In the case of a static black hole it is unclear exactly what is meant by ‘early’ (i.e. if this means a short time before the end of evaporation, or in the remote past). In the present case we have both a beginning and an end to the evaporation process: when the tunnelling surface is exposed and when the black hole evaporates completely. This allows an investigation of whether the radiation emitted between these times can contain any information about the structure that collapsed to form the hole. That the tunnelling surface is known to be separate from the global event horizon indicates that this may be the case, as the modes that are infinitely suppressed as the horizon is approached can then be non-zero. In section 2 we consider the geometry of the system. The mass of the hole is made to decrease as a function of the time coordinate used in the tunnelling calculation [2] (the proper time of a freely falling observer). The resulting line-element is then transformed into double null coordinates, as in [5]. In section 3 we discuss the separation of the global event horizon from the surface \(r=2m\). The tunnelling calculation suggests that the outgoing radiation is emitted from \(r=2m\), and not the global horizon. This is in good agreement with the results of [16, 17, 18]. Section 4 contains a calculation of the renormalised vacuum expectation value of the energy-momentum tensor in the two dimensional analogue of this space-time, as prescribed by the point splitting method of Davies and Fulling [9]. The corresponding energy-momentum tensor in the Vaidya space-time has been considered in [10, 11]. In section 5 we use the results of the previous calculations to consider the radiation measured by an external observer watching a spherical collapse, and show the extent to which this radiation is effected by the process that formed the hole. A discussion is provided in section 6. ## 2 Geometry of the system A natural choice for the parameterisation of tunnelling events through the horizon is the proper time of a radially in-falling observer. This is given by the Panlevé time [12], or river time, \(t\), used by Parikh and Wilczek in their calculation of the rate of these events [2]. For a black hole geometry with constant mass, this time coordinate is related to the more usual Schwarzschild time, \(t_{S}\), by \[t=t_{S}+2\sqrt{2mr}+2m\ln\frac{\sqrt{r}-\sqrt{2m}}{\sqrt{r}+\sqrt{2m}}.\] (1) The Schwarzschild metric can then be written as \[ds^{2}=\left(1-\frac{2m}{r}\right)dt^{2}-2\sqrt{\frac{2m}{r}}dtdr-dr^{2}-r^{2} d\Omega^{2}.\] (2) When considering events occurring at \(r=r_{2m}\equiv 2m\) this coordinate system has a number of advantages over Schwarzschild coordinates. Firstly, surfaces of constant \(t\) cross the surface \(r=r_{2m}\), allowing events along \(r_{2m}\) to be assigned a time at which they occur. Secondly, as mentioned above, \(t\) corresponds to the proper time of a freely falling observer along a radial geodesic parameterised by \(\dot{r}=-\sqrt{2m/r}\) (over-dots denote differentiation with respect to \(t\) throughout). Furthermore, surfaces of constant \(t\) are simply Euclidean 3-spaces. To account for the reduction in mass of the hole due to tunnelling we now parameterise \(m\) as \(m(t)\). (If one were to attempt such a parameterisation in terms of \(t_{S}\) then a curvature singularity would appear at \(r_{2m}\)). This time-dependent Panlevé geometry is the one considered by Brown and Lindesay in [4, 5, 6]. We consider it to be the continuum limit of the near horizon geometry that results from many small, discrete tunnelling events. For simplicity we consider radiated particles to be s-waves, so that by Birkhoff’s theorem their effects on the geometry of the hole can be neglected, other than by reducing the value of \(m\). This geometry is similar to the Vaidya metric, but here the mass, \(m\), is made a function of the Panlevé time, \(t\), used in the tunneling calculation, instead of the advanced time, \(v_{s}=t_{s}+r\). This geometry allows the mass loss due to tunneling to be taken into account straightforwardly, as well as allowing the metric to be cast in double null co-ordinates in a simple way. Consider the retarded and advanced null coordinates [5] \[du =A\left(1-\sqrt{\frac{2m}{r}}\right)dt-Adr\] (3) \[dv =B\left(1+\sqrt{\frac{2m}{r}}\right)dt+Bdr,\] (4) where \(A=A(t,r)\) and \(B=B(t,r)\) must satisfy the integrability conditions \[\frac{\partial}{\partial r}\left(\left(1-\sqrt{\frac{2m}{r}} \right)A\right)+\frac{\partial A}{\partial t} =0\] (5) \[\frac{\partial}{\partial r}\left(\left(1+\sqrt{\frac{2m}{r}} \right)B\right)-\frac{\partial B}{\partial t} =0.\] (6) If \(m=\)constant then these equations have the simple solutions \(A=1/(1-\sqrt{2m/r})\) and \(B=1/(1+\sqrt{2m/r})\), corresponding to the Schwarzschild solution in null coordinates. If \(m=m(t)\) then for a slowly evaporating black hole we can approximate \(m\) by an expansion about some early moment, \(t_{0}\), so that \(m(t)\simeq m(t_{0})+\dot{m}(t_{0})t\). To this order of approximation equations (5) and (6) have the solutions \[A =\prod_{i}\left(x_{i}-\sqrt{\frac{2m}{r}}\right)^{\frac{x_{i}}{2- 3x_{i}}}\] (7) \[B =\prod_{i}\left(y_{i}+\sqrt{\frac{2m}{r}}\right)^{\frac{y_{i}}{2- 3y_{i}}}\] (8) where \(x_{i}\) are the roots of \(2\dot{m}-x^{2}+x^{3}=0\), and \(y_{i}\) are the roots of \(2\dot{m}+y^{2}-y^{3}=0\). In terms of the new coordinates, defined by (3) and (4), the line-element (2) then takes the form \[ds^{2}=\frac{dudv}{AB}-r^{2}d\Omega^{2},\] (9) where \(A\) and \(B\) are given by (7) and (8). This geometry will be used to describe the region outside a shell of matter that collapses to form a radiating black hole. Inside, the geometry will be taken to be Minkowski space covered by the retarded and advanced null coordinates, \(U=T-r\) and \(V=T+r\), such that \(ds^{2}=dUdV-r^{2}d\Omega^{2}\). The two sets of null coordinates in the two regions can then be related at the boundary between them by the transformations \(\alpha(u)=U\) and \(\beta(V)=v\). If this boundary is at a radial distance \(r=R(t)\), then these functions are given by the differential relations \[\alpha^{\prime} =\frac{dU}{du}=\frac{\sqrt{1-\frac{2m}{R}-2\sqrt{\frac{2m}{R}} \dot{R}}-\dot{R}}{A\left(1-\sqrt{\frac{2m}{R}}-\dot{R}\right)}\] (10) \[\beta^{\prime} =\frac{dv}{dV}=\frac{B\left(1+\sqrt{\frac{2m}{R}}+\dot{R}\right)} {\sqrt{1-\frac{2m}{R}-2\sqrt{\frac{2m}{R}}\dot{R}}+\dot{R}}.\] (11) ## 3 Tunnelling and the horizon An important feature of the geometry (2) is that the global event horizon (the boundary of the past of future null infinity) is _not_ at \(r=2m\). It is displaced by a small amount¹[4, 5, 6]. As the global event horizon is a null surface it is described by the outgoing null geodesics [FOOTNOTE:1][ENDFOOTNOTE] \[\dot{r}_{H}=1-\sqrt{\frac{r_{2m}}{r_{H}}},\] (12) so that \(r_{H}=r_{2m}\) only when \(\dot{r}_{H}\to 0\), the limit where the black hole is not evaporating. For an evaporating hole we have \(\dot{r}_{H}<0\), and so \(r_{H}<r_{2m}\). Under the approximation \(m(t)=m(t_{0})+\dot{m}(t_{0})t\) the location of \(r_{H}\) can then be seen to be given by the positive real solution of \[2\dot{m}-\frac{r_{2m}}{r_{H}}+\left(\frac{r_{2m}}{r_{H}}\right)^{3/2}=0.\] (13) This is exactly the point at which \(A\) becomes singular, as can be seen from (7). The Penrose diagram for this geometry (see [5] for details) is shown in figure 1, where the global horizon at \(r_{H}\) is represented by a dashed line and the surface \(r=2m\) is given by a dotted line. The thick solid line represents the trajectory of the shell, \(R(t)\). [FIGURE:S3.F1][ENDFIGURE] The question now arises, through which surface are the radiated particles tunnelling: \(r=r_{2m}\) or \(r=r_{H}\)? To answer this let us consider the rate of tunnelling \(\Gamma\sim\exp\{-2\text{Im S}\}\), where S is the action along the classically forbidden trajectory. Using Hamilton’s equation, \(\dot{r}=dH/dp_{r}|_{r}\), Parikh and Wilczek [2] find the exponent of this rate to be \[-2\text{Im S}=-2\text{Im}\int_{r_{in}}^{r_{out}}p_{r}dr=-2\text{Im}\int_{r_{in }}^{r_{out}}\int_{0}^{p_{r}}dp_{r}^{\prime}dr=-2\text{Im}\int\int\frac{dr}{ \dot{r}}dH.\] (14) Here \(p_{r}\) is the radial momentum of the particle that is tunnelling from \(r_{in}\) to \(r_{out}\). The particles trajectory \(\dot{r}\) is then given by the null geodesics of (2) with \(m\) replaced by \(m-\omega\), where \(\omega\) is the energy of the particle. They then swap the order of integration and obtain \[-2\text{Im S}=-2\text{Im}\int_{0}^{\omega}\int_{r_{in}}^{r_{out}}\frac{dr}{1- \sqrt{\frac{2(m-\omega^{\prime})}{r}}}(-d\omega^{\prime})=-8\pi\omega\left(m- \frac{\omega}{2}\right)\] (15) where the final expression is given provided \(r_{in}>r_{out}\). It is then noted that if they had instead kept the original order of integration they would have found \[-2\text{Im S}=-2\text{Im}\int_{r_{in}}^{r_{out}}\int_{m}^{m-\omega}\frac{dm^{ \prime}}{1-\sqrt{\frac{2m^{\prime}}{r}}}dr=2\pi\int_{r_{in}}^{r_{out}}rdr.\] (16) If \(r_{out}=r_{in}-2\omega\), the value of \(r_{in}\) is then \(2m\). This shows that the tunnelling events occur through the surface \(r_{2m}\), where the action obtains an imaginary part. This is distinct from the global event horizon at \(r=r_{H}\). For further details the reader is referred to the original text [2], and for criticisms and discussion to [13]. This result has also be generalised to other cases [14]. The idea that radiation should be emitted from a surface outside the horizon is not new: It has been considered by Visser [16], di Criscienzo _et al_[17], and Nielsen [18], as well by Susskind, Thorlacius and Uglum [19] in the form of a ‘stretched horizon’. The stretched horizon was envisaged as a place where information about the micro-physical structure of objects falling into a black hole could be stored, and subsequently encoded in outgoing radiation. In the present study, as in [16, 17, 18], this surface is the place where an outgoing particle trajectory is classically forbidden. Such a surface is a physically meaningful concept at finite times, unlike the surface \(r=r_{H}\) which requires a knowledge of the global structure of space-time in order to be defined. ## 4 The energy-momentum of radiation We will now compute the vacuum expectation value of the energy-momentum tensor of a massless conformal scalar field in the vicinity of the surface \(r_{2m}\), outside of a collapsing shell of matter. This calculation will be in two dimensions and will follow the study of Davies [8], which was performed with \(m=\)constant. The regularisation method employed will be the point splitting method of Davies and Fulling [9]. In this method the product of field operators in the energy-momentum tensor are evaluated as functions of two points along a geodesic. The points are then brought together, and the divergent terms covariantly subtracted. The result is a non-divergent and covariant, renormalised vacuum expectation value for the energy-momentum tensor. Although the two dimensional case has proved a useful tool in understanding semi-classical radiation, one should keep in mind that it may not be exactly analogous to the corresponding case in four dimensions [20]. This method has been previously applied to dynamical black hole space-times in [10, 11]. Following [21] we introduce a new system of null coordinates, \(\bar{u}\) and \(\bar{v}\), that cover the space-time both inside and outside the shell of radius \(R(t)\). The metric is then given by \[ds^{2}=C(\bar{u},\bar{v})d\bar{u}d\bar{v}\] (17) where \[C(\bar{u},\bar{v})= \frac{dU}{d\bar{u}}\frac{dV}{d\bar{v}}\qquad r<R(t)\] \[= \frac{1}{AB}\frac{du}{d\bar{u}}\frac{dv}{d\bar{v}}\qquad r>R(t).\] As this metric is conformally flat, the solutions of the scalar wave equation are the solutions of \(\phi_{,\bar{u}\bar{v}}=0\), which are simply \(e^{-i\omega\bar{v}}\) and \(e^{-i\omega\bar{u}}\). The choice \(\bar{v}=v\) ensures these fields can be made to correspond with their usual form in Minkowski space at past null infinity. Furthermore, choosing \(\bar{u}=\beta(U)\) means that outgoing waves \(e^{-i\omega\bar{u}}\) can be matched to incoming waves \(e^{-i\omega v}\) at \(r=0\), allowing a simple correspondence as they pass through the centre of the shell. The point splitting procedure of [9] now yields the renormalised energy-momentum tensor for a massless conformal field in the geometry (17) as \[T_{\bar{\mu}\bar{\nu}}=\theta_{\bar{\mu}\bar{\nu}}+\frac{R}{48\pi}g_{\bar{\mu} \bar{\nu}}\] (18) where \(\theta_{\bar{u}\bar{u}}=-F_{\bar{u}}(C)\), \(\theta_{\bar{v}\bar{v}}=-F_{\bar{v}}(C)\), \(\theta_{\bar{u}\bar{v}}=\theta_{\bar{v}\bar{u}}=0\) and \(F_{x}(y)=(12\pi)^{-1}y^{1/2}(y^{-1/2})_{,xx}\). The components of this tensor can be evaluated using the relations specified above between the three coordinate systems. Inside the shell the non-zero components are, in \(U\) and \(V\) coordinates, \[T_{UU} =F_{U}(\beta^{\prime}(U))\] (19) \[T_{VV} =F_{V}(\beta^{\prime}(V)),\] (20) whilst outside the shell we have, in \(u\) and \(v\) coordinates, \[T_{uu} =\frac{1}{3A^{2}}F_{r}\left(e^{-3\sqrt{\frac{2m}{r}}}\right)+ \frac{1}{A^{2}}F_{r}(A)+\sqrt{\frac{2m}{r}}\frac{\dot{m}}{192\pi rmA^{2}}+{ \alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))+F_{u}(\alpha^{\prime}(u))\] (21) \[T_{vv} =\frac{1}{3B^{2}}F_{r}\left(e^{3\sqrt{\frac{2m}{r}}}\right)+\frac {1}{B^{2}}F_{r}(B)+\sqrt{\frac{2m}{r}}\frac{\dot{m}}{192\pi rmB^{2}}\] (22) \[T_{uv} =T_{vu}=-\frac{1}{192\pi rAB}\left(\frac{8m}{r^{2}}+\sqrt{\frac{2 m}{r}}\frac{\dot{m}}{{m}}\right),\] (23) where \(A\), \(B\), \(\alpha^{\prime}\) and \(\beta^{\prime}\) are given by (7), (8), (10) and (11). The expressions (19)-(23) now give the required form of the energy-momentum tensor for a scalar field in the presence of a collapsing shell of matter, and will be used below to investigate the energy density of radiation measured by observers watching the collapse. ## 5 Measurements made by asymptotic observers ### \(\mathbf{m=\text{constant}}\) Let us briefly review the static limit, \(m\rightarrow\text{constant}\), so that \(A\to 1/(1-\sqrt{2m/r})\), \(B\to 1/(1+\sqrt{2m/r})\) and the results of [8] are retrieved. In this case the third terms in (21) and (22), and the second term in (23), are zero everywhere. The first two terms in each of (21) and (22) are identical, and, along with the first term of (23), represent an energy density in the vicinity of the black hole due to the curvature of Schwarzschild space-time. This energy density vanishes in the limit \(r\rightarrow\infty\), and does not contribute to the Hawking radiation measured by asymptotic observers. The remaining two terms of (21) are functions of the retarded time coordinates only, and can therefore give a non-zero energy density at future null infinity. The last of these terms, \(F_{u}(\alpha^{\prime}(u))\), is a function of \(R(t)\) for finite \(u\). As \(u\rightarrow\infty\), however, it approaches \(1/768\pi m^{2}\) and so corresponds to the Hawking term. The penultimate term in (21), \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\), matches the mode inside the shell, given by equations (19) and (20), which is initially in-going, then passes through the centre at \(r=0\) before becoming an outgoing ray that passes back out through the shell and on to future null infinity. This term is sensitive to the form of \(R(t)\), and its pre-factor of \({\alpha^{\prime}}^{2}\), due to the transformation from \(U\) to \(u\), is non-zero for finite \(u\). As \(u\rightarrow\infty\), however, \(\alpha^{\prime}\to 0\) so that the contribution of this term vanishes in that limit. When \(m=\text{constant}\) the only relevant non-zero term as \(u\rightarrow\infty\) is therefore the Hawking one, which is a constant, independent of the process that formed the black hole (i.e. independent of \(R(t)\)). For finite \(u\) this is not the case, and the flux of radiation reaching future null infinity is sensitive to the collapse process. Whether this corresponds to any useful information reaching the asymptotic observer is unclear, as in this case surfaces of finite \(u\) can be removed to the distant past by the stacking of surfaces of constant \(u\) against the event horizon. We will now investigate the case in which \(\dot{m}\neq 0\). As discussed above the source of the radiation in this case is expected to be the surface \(r=r_{2m}\), which is displaced from the global event horizon at \(r_{H}\). ### \(\mathbf{m\neq\text{constant}}\) It can be seen that when \(\dot{m}\neq 0\) the first two terms of (21) and (22), and the first term of (23), are still independent of the collapse process. Their forms are modified from the \(\dot{m}=0\) case, as the two functions \(A\) and \(B\) are now given by (7) and (8), but they still approach zero as \(r\rightarrow\infty\). When \(\dot{m}\neq 0\) we now have three new terms: The third terms in (21) and (22), and the second term in (23). These terms also vanish as \(r\rightarrow\infty\), and so do not contribute to any flux at future null infinity². [FOOTNOTE:2][ENDFOOTNOTE] The only non-zero components of the energy-momentum tensor, as \(r\rightarrow\infty\), are therefore \[T_{uu}\rightarrow{\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))+F_{u}(\alpha ^{\prime}(u)).\] These are the same two terms that contribute to the asymptotic flux in the \(\dot{m}=0\) case, but now the \(\alpha\) and \(\beta\) terms, as well as the coordinate transformations between \(u\), \(U\) and \(t\), are modified by the non-constant \(m(t)\). Substituting (7), (8), (10) and (11) into the expression above, together with the relevant transformations from \(u\) and \(U\) to \(t\), allows these two terms to be evaluated as functions of \(t\). Due to the complicated form of the resulting expressions we choose not to show them explicitly here, but rather to present them as plots. This will demonstrate how the present case differs from the \(m=\text{constant}\) case, which we will display in parallel for comparison. For illustrative purposes let us consider \(m=1-0.01t\) and \(R=2-0.6t\), so that \(R=r_{2m}\) at \(t=0\). The trajectories of \(R\), \(r_{2m}\) and \(r_{H}\) are then shown in figure 2 as the solid line, the dotted line and the dashed line, respectively. Before \(t=0\) the shell is outside of both \(r_{2m}\) and \(r_{H}\). Between \(t=0\) and \(t\simeq 0.13\) the shell is between \(r_{2m}\) and \(r_{H}\), and after \(t\simeq 0.13\) the shell is inside the global horizon. We will refer to this choice of parameters as “hole 1”. [FIGURE:S5.F2][ENDFIGURE] \(F_{u}(\alpha^{\prime}(u))\) for hole 1 can be readily calculated and is shown in figure 3(a) as a function of \(t\) along the trajectory \(R(t)\). Similarly, \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) is shown in figure 3(b). These plots have been normalised so that \(F_{u}(\alpha^{\prime}(u))=1\) when \(R=r_{H}\), the moment the shell crosses the global event horizon. For comparison we also show in figures 3(a) and 3(b) the results that would have been obtained for a black hole evaporating at half the rate (“hole 2”, the dotted lines) and a black hole with constant mass (“hole 3”, the dashed lines). In both of these cases the trajectory of the in-falling shell is kept the same as for hole 1, and both have been chosen so that the \(r_{H}\) of all three holes are equal at the moment \(R=r_{H}\). [FIGURE:S5.F3][ENDFIGURE] It can be seen from figure 3 that the value of \(F_{u}(\alpha^{\prime}(u))\) for hole 3 is approximately constant over the time scale being considered, at the Hawking rate of \(1/768\pi m^{2}\). For holes 1 and 2 \(F_{u}(\alpha^{\prime}(u))\) can be seen to be a slowly increasing function of \(t\), that becomes rapidly increasing as \(R\to r_{H}\). The value of \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) can be seen to approach zero for all three holes as \(R\to r_{H}\), as expected. This is due to \({\alpha^{\prime}}(u)\to 0\) in this limit. Let us now consider what the observer at infinity measures. To find this we must transform the plots above from \(t\) to \(t_{\infty}\), the proper time of an asymptotic observer, by \[dt_{\infty}=\left[A(t)\left(1-\sqrt{\frac{2m(t)}{R(t)}}-\dot{R}(t)\right) \right]dt.\] (24) This expression relates the two time coordinates via the retarded time \(u\). The two terms \(F_{u}(\alpha^{\prime}(u))\) and \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) are now given as function of \(t_{\infty}\) in figures 4(a) and 4(b). These plots are normalised by the value of \(F_{u}(\alpha^{\prime}(u))\) for hole 1 at \(R=r_{H}\), and the new time coordinate for holes 1 and 2 have been chosen so that \(t_{\infty}=0\) when the asymptotic observer sees \(R=r_{2m}\). (This is not possible in the static case as the surface \(r_{2m}\) is degenerate with \(r_{H}\)). Units have been chosen so that \(t_{\infty}=1\) when the asymptotic observer sees \(R=r_{H}\), in each case. [FIGURE:S5.F4][ENDFIGURE] These plots are the same as those of figure 3, but they have been stretched near \(R=r_{H}\) and squashed near \(R=r_{2m}\), giving them a considerably different appearance. The stretching involved increases as the rate of evaporation decreases, diverging in the limit of a static hole. Hence the lines corresponding to hole 3 are now straight, and equal to zero in the case of figure 4(b). The observer at infinity watching holes 1 and 2 sees an energy density in the mode \(F_{u}(\alpha^{\prime}(u))\) that rises as the shell is seen to pass \(r_{2m}\), and subsequently increases at a steady rate. This is due to the surfaces of constant \(u\) stacking up against the global horizon, and stretching out the spikes seen in figure 3(a). That the radiation increases as the shell crosses \(r_{2m}\) is in support of the conjecture that the radiation is originating from this surface, as found directly in the tunnelling calculation. Figure 4(b) shows that for holes 1 and 2 the contribution from \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\), as witnessed by the asymptotic observer, becomes exponentially small soon after the shell crosses \(r_{2m}\). Again, this is due to the stacking of surfaces of constant \(u\) against the global horizon, and the resulting stretching of figure 3(b). In the vicinity of \(R=r_{2m}\), however, while this component is small, it is still non-zero. This is of interest as \(F_{U}(\beta^{\prime}(U))\) is known to be sensitive to the collapse process that formed the hole [8]. To consider the degree to which the outgoing radiation is sensitive to the collapse process, let us now perturb the in-falling trajectory of the shell by a small amount, so that \(R=3\times 10^{-5}\cos(10^{2}t)+2-0.6t\). This is a small enough perturbation that the plot of the trajectory of the in-falling shell is indistinguishable from figure 2. However, the effects on \(F_{u}(\alpha^{\prime}(u))\) and \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) are not negligible, and are shown in figure 5. The same scalings and origin have been chosen as above. Perturbations to the infall trajectory could result from imperfections in spherical symmetry, internal stresses, or interactions of the shell with other objects. Here we simply wish to illustrate the sensitivity of the emitted raditiation to the collapse process, and so add an _ad hoc_ oscillation to the shell’s trajectory. It can be seen such oscillations, although small, have a discernible effect on the outgoing radiation of the holes. Both functions \(F_{u}(\alpha^{\prime}(u))\) and \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) can be seen to oscillate around their unperturbed values, as shown in figure 3. These oscillations are particularly apparent in \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\). [FIGURE:S5.F5][ENDFIGURE] Now let us consider the radiation measured by an asymptotic observer watching the perturbed shell collapse. Any features present in the plots in figure 5 should also be present in the radiation he/she measures, although it will be effected by the stretching and squashing involved in the transformation from \(t\) to \(t_{\infty}\). Using (24) we find that \(F_{u}(\alpha^{\prime}(u))\) and \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) are given as functions of \(t_{\infty}\) as shown in figure 6. For holes 1 and 2, the oscillations that were present in figure 5 are again apparent, but now restricted to be observable only in the vicinity of \(R=r_{2m}\) (due to the stacking of surfaces of constant \(u\) against the global horizon). The infinite stretching in the case of hole 3 is enough to remove the oscillations that were present in figure 5 to the infinite past. [FIGURE:S5.F6][ENDFIGURE] ## 6 Discussion We have considered the case of a black hole that forms from the collapse of a spherical shell, and decays via tunnelling events. In this case the mass parameter of the hole is made a function of the Panlevé time, \(t\), and the surface \(r=2m\) separates from the global event horizon by a small amount. The tunnelling events occur at \(r=2m\), and not at the global event horizon. This displacement has consequences for the emission of Hawking radiation, and for its observation by asymptotic observers watching the collapse. The energy-momentum tensor of a massless conformal scalar field is obtained in the two dimensional analogue of this space-time, and the flux of radiation measured by an asymptotic observer is calculated. The asymptotic observer witnesses radiation that initially increases at about the time he/she sees the collapsing shell cross \(r=2m\), and increases at a steady rate thereafter. This supports the idea that the Hawking radiation is emitted from the vicinity of the surface \(r=2m\)[16, 17, 18], and that after this surface is exposed to asymptotic observers he/she witnesses radiation from a hole that is slowly increasing in temperature. Radiation originating from outside of the global event horizon contains modes that are sensitive to the collapse process [8]. This sensitivity is illustrated by perturbing the collapsing shell with a small oscillation. The effects of this on the modes that escape to future null infinity are clearly visible, and only vanish in the limit that the global horizon is approached. For the static model the infinite stacking of surfaces of constant retarded time against the global horizon removes these modes to the remote past, so that it is unclear whether they have any observational significance. This is not the case in the non-static models. Here the sensitivity of the emitted radiation to the collapse process is clearly visible, but restricted to be observable only at the beginning of the evaporation process. Nevertheless, an observer who measures all of the radiation emitted from the hole may, in principle, be able to extract some information about the collapse process that formed it. There are a number of ways in which this study could be improved. In particular, one could parameterise \(m\) as a function of \(t\) in a more satisfactory way. Here we assumed a function of the form \(m=m_{0}+\dot{m}_{0}t\), in order to get explicit, exact solutions. While this is likely to be valid for the early stages of evaporation (being the first term of a series expansion), it is unlikely to be a good approximation during the late stages. Ideally one would like to find solutions with more general \(m(t)\). A further problem is the behaviour of the model as \(m\to 0\), when the black hole evaporates completely [10, 22]. In this limit (depending on the form of \(m(t)\)) the scalar curvature invariants associated with the space-time (2) may diverge, indicating a singularity³. This shows that a continuum limit for \(m(t)\) is not appropriate at the end point of evaporation, and that a cutoff should be introduced beyond which a more appropriate method is used. [FOOTNOTE:3][ENDFOOTNOTE] **Acknowledgements** I am grateful to Pedro Ferreira and Philip Candelas for helpful discussions, and to Jesus College for support. ## References * [1] S. W. Hawking, Comm. Math. Phys. **43**, 199 (1975). * [2] M. K. Parikh and F. Wilczek, Phys. Rev. Lett. **85**, 5042 (2000). * [3] P. Kraus and F. Wilczek, Nucl. Phys. B **433**, 403 (1995). E. Keski-Vakkuri and P. Kraus, Nucl. Phys. B **491**, 249 (1997). * [4] J. Lindesay, Foundations of Physics **37**, 1181 (2007). * [5] B. A. Brown and J. Lindesay, arXiv:0710.2032 (2007). * [6] B. A. Brown and J. Lindesay, arXiv:0802.1660 (2008). * [7] T. Vachaspati, D. Stojkovic and L. M. Krauss, Phys. Rev. D **76**, 024005 (2007). T. Vachaspati and D. Stojkovic, Phys. Lett. B **663**, 107 (2008). * [8] P. C. W. Davies, Proc. R. Soc. Lond. **351**, 129 (1976). * [9] P. C. W. Davies and S. A. Fulling, Proc. R. Soc. Lond. **348**, 393 (1975). * [10] W. A. Hiscock, Phys. Rev. D **23**, 2813 (1981). * [11] R. Balbinot, Phys. Rev. D **33**, 1611 (1986). * [12] P. Panlevé, C. R. Acad. Sci. (Paris) **173**, 677 (1921). * [13] B. D. Chowdhury, Pramana **70**, 593 (2008). E. T. Akhmedov, V. Akhmedova and D. Singleton, Phys. Lett. B **642**, 124 (2006). E. T. Akhmedov, V. Akhmedova, T. Pilling and D. Singleton, Int. J. Mod. Phys. A **22**, 1705 (2007). V. Akhmedova, T. Pilling and A. de Gill and D. Singleton, arXiv:0804.2289, (2008). T. K. Nakamura, arXiv:0706.2916 (2007). P. Mitra, Phys. Lett. B **648**, 240 (2007). * [14] K. Srinivasan and T. Padmanabhan, Phys. Rev. D **60**, 24007 (1999). S. Hemming and E. Keski-Vakkuri, Phys. Rev. D **64**, 044006 (2001). S. Shankaranarayanan, T. Padmanabhan and K. Srinivasan, Class. Quant. Grav. **19**, 2671 (2002). A. J. M. Medved, Phys. Rev. D **66**, 124009 (2002). E. C. Vagenes, Phys. Lett. B **559**, 65 (2003). T. Padmanabhan, Mod. Phys. Lett. A **19**, 2637 (2004). A. J. M. Medved and E. C. Vagenas, Mod. Phys. Lett. A **20**, 2449 (2005). M. Arzano, A. J. M. Medved and E. C. Vargenas, JHEP **0509**, 037 (2005). Q. Q. Jiang, H. L. Li, S. Z. Yang and D. Y. Chen, Mod. Phys. Lett. A **22**, 891 (2007). * [15] S. A. Haywood, Phys. Rev. Lett. **96**, 031103 (2006). A. B. Nielsen, arXiv:0711.0313 (2007). A. B. Nielsen, arXiv:0804.4435 (2008). * [16] M. Visser, Int. J. Mod. Phys. D **12**, 649 (2003). * [17] R. Di Criscienzo, M. Nadalini, L. Vanzo, S. Zerbini and G. Zoccatelli, arXiv:0707.4425 (2007). * [18] A. B. Nielsen, arXiv:0802.3442 (2008). * [19] L. Susskind, L. Thorlacius and J. Uglum, Phys. Rev. D **48**, 3743 (1993). * [20] V. Frolov, P. Sutton and A. Zelnikov, Phys. Rev. D **61**, 024021 (1999). * [21] P. C. W. Davies, S. A. Fulling and W. G. Unruh, Phys. Rev. D **13**, 2720 (1976). * [22] T. P. Singh and C. Vaz, Phys. Lett. B **481**, 74 (2000).

# Свойства излучения черной дыры от туннелирования Черная дыра является астрономическим объектом, обладающим своеобразным свойством излучения. Оно также известно как "излучение Гоккинга-Хэвкинга". Это излучение происходит из горизонта событий черной дыры. Возникает впечатление, что черная дыра испускает черный тепловой излучатель с постоянной температурой. Это излучение можно объяснить феноменом туннелирования в квантовой механике. Квантовые флуктуации приводят к появлению и регенерации частиц-античастиц вблизи радиуса черной дыры. Одна из частиц поглощается черной дырой, а другая выплывает в открытый мир в качестве излучения. Формула для расчета температуры черной дыры: $$ T = \frac{ħc^3}{8\pi G M} $$ Здесь: - T - температура черной дыры - ħ - постоянная Планка, равная 6.62607015 * 10^(-34) Дж∙с - c - скорость света, приближенно равная 3 * 10^8 м/с - G - гравитационная постоянная, приближенно равная 6.67430 * 10^(-11) м^3∙кг^(-1)∙с^(-2) - M - масса черной дыры Следует отметить, что туннелирование излучения черной дыры имеет важные последствия и является одним из ключевых факторов при изучении черных дыр и их эволюции. Тимоти Клифтон _Отдел астрофизики Университета Оксфорда, Оксфорд OX1 3RH, Великобритания_ e-mail: [email protected] (11 февраля 2024 года) ###### Аннотация Мы рассматриваем пространство-время, связанное с испарением черной дыры через квантово-механические процессы туннелирования. Показано, что поверхность, через которую происходит туннелирование, отличается от глобального горизонта событий, и что это имеет последствия для излучения, достигающего будущего нулевого бесконечности. Моделируется процесс сферического коллапса, и рассчитывается излучение, ожидаемое наблюдать в будущем нулевом бесконечности. Показано, что внешние наблюдатели видят процесс испарения, который начинается, когда поверхность туннелирования обнажается, и заканчивается, когда коллапсирующий объект проходит за свой горизонт событий. Иллюстрируется чувствительность излучения к процессу коллапса. ## 1 Введение Один из общих интерпретаций Хокинговского излучения [1] связан с явлением квантового туннелирования виртуальных частиц через горизонт. В этой модели виртуальная пара образуется непосредственно внутри (или непосредственно снаружи) горизонта событий. Квантовое механическое событие затем переносит частицу с положительной энергией изнутри горизонта наружу (или частицу с отрицательной энергией извне внутрь). В результате реальная частица материализуется вне черной дыры, а масса дыры уменьшается. Это давно рассматриваемое эвристическое объяснение Хокинговского излучения недавно получило прочную основу благодаря работе Париха и Вилчека [2]. Расчет, проведенный ими, принимает во внимание изменение геометрии пространства-времени в процессе туннелирования и предоставляет естественную временную координату, с помощью которой можно параметризовать потерю массы дыры, а также определить местоположение источника излучения. Интересно, что было показано, что спектр излучения не является точным чёрным излучением, как ранее было показано в [3], хотя не было ясно, как это можно связать с процессом коллапса, породившего дыру. Здесь мы рассматриваем процесс коллапса, приводящий к формированию и последующему испарению черной дыры. Мы моделируем это как коллапсирующую сферическую оболочку материи. После образования дыры предполагается, что её масса уменьшается процессом туннелирования, описанным выше. Результирующая геометрия (как ранее рассмотрено Брауном и Линдси [4, 5, 6]) имеет глобальный горизонт событий, отстоящий от точки излучения. Затем вычисляется энергомонентка покидающего излучения. Как и ожидалось, обозреватель, наблюдающий коллапс издалека, видит увеличение потока излучения, так как он подвергается поверхности, через которую происходит туннелирование. Это выглядит для внешнего наблюдателя, как будто излучение испускается до того, как коллапсирующий объект пересекает свой собственный горизонт событий. Поток излучения продолжает увеличиваться до достижения горизонта событий. Аналогичные результаты, полученные альтернативным методом, были найдены в [7]. Это представляет интерес определить чувствительность излучения к процессу коллапса, приводящему к формированию черной дыры. Как известно, в пределе при приближении к горизонту событий вся информация о коллапсе исчезает. Только раннее излучение чувствительно к нему [8]. В случае статической черной дыры неясно, что именно подразумевается под "ранним" (т.е. если это означает короткое время до конца испарения или в отдаленном прошлом). В данном случае у нас есть начало и конец процесса испарения: когда туннельная поверхность становится видимой и когда черная дыра полностью испаряется. Это позволяет исследовать, может ли излучение, излучаемое между этими временами, содержать какую-либо информацию о структуре, которая рухнула, чтобы образовать дыру. Тот факт, что туннельная поверхность известна как отдельная от глобального горизонта событий, указывает на то, что это может быть так, поскольку моды, бесконечно подавляемые при приближении к горизонту, могут быть ненулевыми. В разделе 2 мы рассматриваем геометрию системы. Масса дыры уменьшается как функция временной координаты, используемой в расчете процесса проникновения [2] (собственное время свободно падающего наблюдателя). Полученный линейный элемент затем преобразуется в двойные нулевые координаты, как в [5]. В разделе 3 мы обсуждаем разделение глобального горизонта событий от поверхности \(r=2m\). Расчет процесса проникновения подразумевает, что исходящее излучение испускается из \(r=2m\), а не из глобального горизонта. Это в хорошем согласии с результатами [16, 17, 18]. Раздел 4 содержит расчет ренормированного вакуумного ожидания энергомоментного тензора в двумерном аналоге этого пространства-времени, как предписано точечным методом разделения Дэвиса и Фуллинга [9]. Соответствующий энергомоментный тензор в пространстве-времени Вайди рассматривался в [10, 11]. В разделе 5 мы используем результаты предыдущих расчетов, чтобы рассмотреть излучение, измеряемое внешним наблюдателем, наблюдающим сферический коллапс и показать, насколько это излучение зависит от процесса, который образовал дыру. Обсуждение представлено в разделе 6. ## 2 Геометрия системы Естественным выбором для параметризации процессов туннелирования через горизонт является собственное время радиально падающего наблюдателя. Оно задаётся временем Панлеве [12], или речным временем, \(t\), используемым Парихом и Вильчеком при расчёте скорости таких событий [2]. Для геометрии черной дыры с постоянной массой, эта временная координата связана с более привычным временем Шварцшильда, \(t_{S}\), следующим соотношением: \[ t = t_{S}+2\sqrt{2mr}+2m\ln\frac{\sqrt{r}-\sqrt{2m}}{\sqrt{r}+\sqrt{2m}}. \] (1) Метрика Шварцшильда может быть записана как \[ds^{2}=\left(1-\frac{2m}{r}\right)dt^{2}-2\sqrt{\frac{2m}{r}}dtdr-dr^{2}-r^{2} d\Omega^{2}.\] (2) При рассмотрении событий, происходящих при \(r=r_{2m}\equiv 2m\), эта система координат имеет несколько преимуществ по сравнению с координатами Шварцшильда. Во-первых, поверхности постоянного \(t\) пересекают поверхность \(r=r_{2m}\), что позволяет событиям вдоль \(r_{2m}\) присваивать время, в которое они происходят. Во-вторых, как уже упоминалось выше, \(t\) соответствует собственному времени свободно падающего наблюдателя по радиальной геодезической, параметризованной \(\dot{r}=-\sqrt{2m/r}\) (точечки над переменными обозначают дифференцирование по \(t\)). Кроме того, поверхности постоянного \(t\) являются просто евклидовыми трехмерными пространствами. Чтобы учесть снижение массы отверстия из-за туннелирования, мы теперь параметризуем \(m\) как \(m(t)\). (Если бы мы попытались сделать такую параметризацию в терминах \(t_{S}\), тогда возникло бы сингулярность кривизны при \(r_{2m}\)). Эта зависящая от времени геометрия Панлеве рассматривается Брауном и Линдсеем в [4, 5, 6]. Мы считаем ее непрерывным пределом геометрии ближней горизонта, которая возникает после множества маленьких дискретных туннельных событий. Для простоты мы считаем, что излучаемые частицы - это с-волны, так что, согласно теореме Биркгоффа, их влияние на геометрию отверстия можно пренебречь, за исключением уменьшения значения \(m\). Эта геометрия похожа на метрику Вайды, но здесь масса \(m\) становится функцией времени Панлеве, \(t\), используемого в расчете туннелирования, вместо прогрессивного времени, \(v_{s}=t_{s}+r\). Эта геометрия позволяет учесть потерю массы из-за туннелирования прямолинейно, а также позволяет привести метрику к двухнаправленным координатам простым способом. Рассмотрим задержанные и опереженные нулевые координаты [5] \[\frac{\partial u}{\partial t} =A\left(1-\sqrt{\frac{2m}{r}}\right)-A\frac{\partial r}{\partial t}\] (3) \[\frac{\partial v}{\partial t} =B\left(1+\sqrt{\frac{2m}{r}}\right)+B\frac{\partial r}{\partial t},\] (4) где \(A=A(t,r)\) и \(B=B(t,r)\) должны удовлетворять условиям интегрируемости \[\frac{\partial}{\partial r}\left(\left(1-\sqrt{\frac{2m}{r}} \right)A\right)+\frac{\partial A}{\partial t} =0\] (5) \[\frac{\partial}{\partial r}\left(\left(1+\sqrt{\frac{2m}{r}} \right)B\right)-\frac{\partial B}{\partial t} =0.\] (6) \[\frac{\partial}{\partial r}\left(\left(1-\sqrt{\frac{2m}{r}} \right)A\right)+\frac{\partial A}{\partial t} =0\] (5) \[\frac{\partial}{\partial r}\left(\left(1+\sqrt{\frac{2m}{r}} \right)B\right)-\frac{\partial B}{\partial t} =0.\] (6) Если \(m=\)const, то эти уравнения имеют простые решения \(A=1/(1-\sqrt{2m/r})\) и \(B=1/(1+\sqrt{2m/r})\), соответствующие Шварцшильдовскому решению в нулевых координатах. Если \(m=m(t)\), то для медленно испаряющейся черной дыры мы можем приближенно описать \(m\) разложением в ряд в некоторый начальный момент \(t_{0}\), так что \(m(t)\simeq m(t_{0})+\dot{m}(t_{0})t\). При этом порядке приближения уравнения (5) и (6) имеют следующие решения: \[A =\prod_{i}\left(x_{i}-\sqrt{\frac{2m}{r}}\right)^{\frac{x_{i}}{2- 3x_{i}}}\] (7) \[B =\prod_{i}\left(y_{i}+\sqrt{\frac{2m}{r}}\right)^{\frac{y_{i}}{2- 3y_{i}}}\] (8) \[А =\prod_{i}\left(x_{i}-\sqrt{\frac{2m}{r}}\right)^{\frac{x_{i}}{2- 3x_{i}}}\] (7) \[Б =\prod_{i}\left(y_{i}+\sqrt{\frac{2m}{r}}\right)^{\frac{y_{i}}{2- 3y_{i}}}\] (8) где \(x_{i}\) являются корнями уравнения \(2\dot{m}-x^{2}+x^{3}=0\), а \(y_{i}\) являются корнями уравнения \(2\dot{m}+y^{2}-y^{3}=0\). В терминах новых координат, определенных уравнениями (3) и (4), линейный элемент (2) принимает вид \[ds^{2}=\frac{dudv}{AB}-r^{2}d\Omega^{2},\] (9) \[ds^{2}=\frac{dudv}{AB}-r^{2}d\Omega^{2},\] (9) где \(A\) и \(B\) определяются (7) и (8). Эта геометрия будет использоваться для описания области вне оболочки материи, которая сжимается и образует излучающую черную дыру. Внутри геометрия будет считаться пространством Минковского, покрытым задержанными и опережающими нулевыми координатами, \(U=T-r\) и \(V=T+r\), такими что \(ds^{2}=dUdV-r^{2}d\Omega^{2}\). Две наборы нулевых координат в двух областях могут быть связаны на границе между ними преобразованиями \(\alpha(u)=U\) и \(\beta(V)=v\). Если эта граница находится на радиальном расстоянии \(r=R(t)\), то эти функции определяются дифференциальными соотношениями \[\alpha^{\prime} =\frac{dU}{du}=\frac{\sqrt{1-\frac{2m}{R}-2\sqrt{\frac{2m}{R}} \dot{R}}-\dot{R}}{A\left(1-\sqrt{\frac{2m}{R}}-\dot{R}\right)}\] (10) \[\beta^{\prime} =\frac{dv}{dV}=\frac{B\left(1+\sqrt{\frac{2m}{R}}+\dot{R}\right)} {\sqrt{1-\frac{2m}{R}-2\sqrt{\frac{2m}{R}}\dot{R}}+\dot{R}}.\] (11) ## 3 Пробуждение и горизонт Важной особенностью геометрии (2) является то, что глобальный горизонт событий (граница прошлого будущего нулевой бесконечности) _не_ находится в \(r=2m\). Он смещен на небольшое расстояние¹[4, 5, 6]. Поскольку глобальный горизонт событий является нулевой поверхностью, он описывается исходящими нулевыми геодезическими. [FOOTNOTE:1][ENDFOOTNOTE] переведите разметку с английского на русский. Сохраните формулы: \[\dot{r}_{H}=1-\sqrt{\frac{r_{2m}}{r_{H}}},\] (12) \[\dot{r}_{H}=1-\sqrt{\frac{r_{2m}}{r_{H}}},\] (12) чтобы \(r_{H}=r_{2m}\) только когда \(\dot{r}_{H}\to 0\), предел, где чёрная дыра не испаряется. Для испаряющейся дыры имеем \(\dot{r}_{H}<0\), и поэтому \(r_{H}<r_{2m}\). Приближенно \(m(t)=m(t_{0})+\dot{m}(t_{0})t\) можно видеть, что положение \(r_{H}\) задается положительным действительным решением \[2\dot{m}-\frac{r_{2m}}{r_{H}}+\left(\frac{r_{2m}}{r_{H}}\right)^{3/2}=0.\] (13) В точности здесь \(A\) становится сингулярным, как видно из (7). Диаграмма Пенроуза для этой геометрии (см. [5] для подробностей) показана на рис. 1, где глобальный горизонт при \(r_{H}\) представлен пунктирной линией, а поверхность \(r=2m\) задается пунктирной линией. Толстая сплошная линия представляет собой траекторию оболочки, \(R(t)\). [FIGURE:S3.F1][ENDFIGURE] - [ФИГУРА:S3.F1][КОНЕЦФИГУРЫ] Теперь возникает вопрос, сквозь какую поверхность проникают излучаемые частицы: \(r=r_{2m}\) или \(r=r_{H}\)? Чтобы ответить на этот вопрос, рассмотрим скорость проникновения \(\Gamma\sim\exp\{-2\text{Im S}\}\), где S - действие вдоль классически запрещенной траектории. Используя уравнение Гамильтона, \(\dot{r}=dH/dp_{r}|_{r}\), Парих и Вильчек [2] находят показатель этой скорости \[-2\text{Im S}=-2\text{Re}\int_{r_{in}}^{r_{out}}p_{r}dr=-2\text{Re}\int_{r_{in}}^{r_{out}}\int_{0}^{p_{r}}dp_{r}^{\prime}dr=-2\text{Re}\int\int\frac{dr}{\dot{r}}dH.\] (14) Здесь \(p_{r}\) - это радиальный импульс частицы, проникающей из \(r_{in}\) в \(r_{out}\). Траектория частицы \(\dot{r}\) затем определяется нулевыми геодезическими (2) с заменой \(m\) на \(m-\omega\), где \(\omega\) - энергия частицы. Затем они меняют порядок интегрирования и получают \[-2\text{Im S}=-2\text{Im}\int_{0}^{\omega}\int_{r_{in}}^{r_{out}}\frac{dr}{1- \sqrt{\frac{2(m-\omega^{\prime})}{r}}}(-d\omega^{\prime})=-8\pi\omega\left(m- \frac{\omega}{2}\right)\] (15) \[-2\text{Им S}=-2\text{Им}\int_{0}^{\omega}\int_{r_{in}}^{r_{out}}\frac{dr}{1- \sqrt{\frac{2(m-\omega^{\prime})}{r}}}(-d\omega^{\prime})=-8\pi\omega\left(m- \frac{\omega}{2}\right)\] (15) где окончательное выражение предоставляется при условии \(r_{in}>r_{out}\). Затем отмечают, что если бы они вместо этого сохранили исходный порядок интегрирования, они бы обнаружили \[-2\text{Im S}=-2\text{Im}\int_{r_{in}}^{r_{out}}\int_{m}^{m-\omega}\frac{dm^{ \prime}}{1-\sqrt{\frac{2m^{\prime}}{r}}}dr=2\pi\int_{r_{in}}^{r_{out}}rdr.\] (16) \[-2\text{Im S}=-2\text{Im}\int_{r_{in}}^{r_{out}}\int_{m}^{m-\omega}\frac{dm^{ \prime}}{1-\sqrt{\frac{2m^{\prime}}{r}}}dr=2\pi\int_{r_{in}}^{r_{out}}rdr.\] (16) Если \(r_{out} = r_{in} - 2\omega\), то значение \(r_{in}\) равно \(2m\). Это показывает, что события туннелирования происходят через поверхность \(r_{2m}\), где действие приобретает мнимую часть. Это отличается от глобального горизонта событий при \(r=r_{H}\). Для дополнительных деталей читатель может обратиться к оригинальному тексту [2], а для критики и обсуждения - к [13]. Этот результат также был обобщен на другие случаи [14]. Идея того, что излучение должно быть испущено с поверхности вне горизонта, не нова: ею занимались Виссер [16], ди Крисченцо и др. [17] и Нильсен [18], а также Сасскинд, Торлачиус и Углум [19] в форме "растянутого горизонта". Растянутый горизонт представлял собой место, где информация о микрофизической структуре объектов, попадающих в черную дыру, могла быть сохранена и затем закодирована в исходящем излучении. В данном исследовании, как и в [16, 17, 18], такая поверхность является местом, где классически запрещен траектория исходящей частицы. Такая поверхность является физически значимой концепцией в конечные моменты времени, в отличие от поверхности \(r=r_{H}\), для определения которой требуется знание глобальной структуры пространства-времени. ## 4 Энергия-импульс излучения Теперь мы вычислим вакуумное ожидание тензора энергии-импульса безмассового конформного скалярного поля вблизи поверхности \(r_{2m}\) вне коллапсирующей оболочки вещества. Этот расчёт будет проводиться в двух измерениях и будет следовать исследованию Дэвиса [8], которое было выполнено при \(m=\)константе. Используемым методом регуляризации будет метод разделения точек Дэвиса и Фуллинга [9]. В этом методе произведение операторов поля в тензоре энергии-импульса вычисляется в виде функций двух точек вдоль геодезической. Затем эти точки приближаются друг к другу, и вычитаются сингулярные слагаемые ковариантным образом. В результате получается недивергентное и ковариантное, ренормализованное вакуумное ожидание тензора энергии-импульса. Хотя двумерный случай оказался полезным инструментом в понимании полуклассического излучения, следует помнить, что он может не быть точно аналогичным соответствующему случаю в четырёх измерениях [20]. Этот метод ранее применялся к динамическим пространство-временам чёрных дыр в [10, 11]. Следуя [21], мы вводим новую систему нулевых координат, \(\bar{u}\) и \(\bar{v}\), которые охватывают пространство-время как внутри, так и снаружи оболочки радиусом \(R(t)\). Метрика тогда определяется следующим образом \[ds^{2}=C(\bar{u},\bar{v})d\bar{u}d\bar{v}\] (17) translates to: \[ds^{2}=C(\bar{u},\bar{v})d\bar{u}d\bar{v}\] (17) We use the equation \(y = mx + b\) to represent a straight line, where \(m\) represents the slope of the line and \(b\) represents the y-intercept. \[C(\bar{u},\bar{v})= \frac{dU}{d\bar{u}}\frac{dV}{d\bar{v}}\qquad r<R(t)\] \[= \frac{1}{AB}\frac{du}{d\bar{u}}\frac{dv}{d\bar{v}}\qquad r>R(t).\] \[С(\bar{u},\bar{v})= \frac{dU}{d\bar{u}}\frac{dV}{d\bar{v}}\qquad r<R(t)\] \[= \frac{1}{AB}\frac{du}{d\bar{u}}\frac{dv}{d\bar{v}}\qquad r>R(t).\] Поскольку этот метрический тензор конформно плоский, решения скалярного волнового уравнения являются решениями \(\phi_{,\bar{u}\bar{v}}=0\), которые просто равны \(e^{-i\omega\bar{v}}\) и \(e^{-i\omega\bar{u}}\). Выбор \(\bar{v}=v\) обеспечивает возможность сопоставления этих полей с их обычной формой в пространстве Минковского при прошлом нулевом бесконечности. Более того, выбор \(\bar{u}=\beta(U)\) означает, что исходящие волны \(e^{-i\omega\bar{u}}\) могут быть сопоставлены с входящими волнами \(e^{-i\omega v}\) при \(r=0\), что позволяет простому сопоставлению, когда они проходят через центр оболочки. Процедура разделения точки из [9] теперь приводит к ренормализованному тензору энергии-импульса для массового конформного поля в геометрии (17) в следующем виде \[T_{\bar{\mu}\bar{\nu}}=\theta_{\bar{\mu}\bar{\nu}}+\frac{R}{48\pi}g_{\bar{\mu} \bar{\nu}}\] (18) \[T_{\bar{\mu}\bar{\nu}}=\theta_{\bar{\mu}\bar{\nu}}+\frac{R}{48\pi}g_{\bar{\mu} \bar{\nu}}\] (18) где \(\theta_{\bar{u}\bar{u}}=-F_{\bar{u}}(C)\), \(\theta_{\bar{v}\bar{v}}=-F_{\bar{v}}(C)\), \(\theta_{\bar{u}\bar{v}}=\theta_{\bar{v}\bar{u}}=0\) и \(F_{x}(y)=(12\pi)^{-1}y^{1/2}(y^{-1/2})_{,xx}\). Компоненты этого тензора могут быть вычислены с использованием указанных выше связей между тремя системами координат. Внутри оболочки ненулевые компоненты равны в координатах \(U\) и \(V\) , \[T_{UU} = F_{U}(\beta^{\prime}(U))\] (19) \[T_{VV} = F_{V}(\beta^{\prime}(V)),\] (20) \[T_{UU} =F_{U}(\beta^{\prime}(U))\] (19) \[T_{VV} =F_{V}(\beta^{\prime}(V)),\] (20) в то время как за пределами оболочки у нас имеются в координатах \(u\) и \(v\) \[T_{uu} =\frac{1}{3A^{2}}F_{r}\left(e^{-3\sqrt{\frac{2m}{r}}}\right)+ \frac{1}{A^{2}}F_{r}(A)+\sqrt{\frac{2m}{r}}\frac{\dot{m}}{192\pi rmA^{2}}+{ \alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))+F_{u}(\alpha^{\prime}(u))\] (21) \[T_{vv} =\frac{1}{3B^{2}}F_{r}\left(e^{3\sqrt{\frac{2m}{r}}}\right)+\frac {1}{B^{2}}F_{r}(B)+\sqrt{\frac{2m}{r}}\frac{\dot{m}}{192\pi rmB^{2}}\] (22) \[T_{uv} =T_{vu}=-\frac{1}{192\pi rAB}\left(\frac{8m}{r^{2}}+\sqrt{\frac{2 m}{r}}\frac{\dot{m}}{{m}}\right),\] (23) где \(A\), \(B\), \(\alpha^{\prime}\) и \(\beta^{\prime}\) заданы (7), (8), (10) и (11). Выражения (19)-(23) теперь дают требуемую форму тензора энергии-импульса для скалярного поля в присутствии коллапсирующей оболочки материи и будут использоваться ниже для изучения энергетической плотности излучения, измеренной наблюдателями, наблюдающими коллапс. ## 5 Измерений, выполненных асимптотическими наблюдателями ### \(\mathbf{m=\text{постоянная}}\) Давайте кратко рассмотрим статический предел, где \(m\rightarrow\text{constant}\), так что \(A\to 1/(1-\sqrt{2m/r})\), \(B\to 1/(1+\sqrt{2m/r})\) и восстанавливаются результаты [8]. В этом случае третий член в уравнениях (21) и (22), а также второй член в уравнении (23), обращаются в ноль во всех точках. Первые два члена в каждом из уравнений (21) и (22) и первый член в уравнении (23) представляют плотность энергии в окрестности черной дыры из-за кривизны пространства-времени Шварцшильда. Эта плотность энергии исчезает при \(r\rightarrow\infty\) и не вносит вклад в излучение Хокинга, измеряемое асимптотическими наблюдателями. Два оставшихся члена выражения (21) являются функциями только от отложенных координат времени и поэтому могут давать ненулевую плотность энергии в будущем бесконечности нулевых инфинитивов. Последний из этих членов, \(F_{u}(\alpha^{\prime}(u))\), является функцией \(R(t)\) при конечном \(u\). Однако при \(u\rightarrow\infty\) он стремится к \(1/768\pi m^{2}\) и соответствует члену Хокинга. Предпоследний член в (21), \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\), соответствует режиму внутренней оболочки, заданному уравнениями (19) и (20), который изначально является входящим, затем проходит через центр при \(r=0\) прежде чем стать исходящим лучом, который проходит обратно сквозь оболочку и далее к будущему нулевому бесконечности. Этот член чувствителен к форме \(R(t)\), и его префактор \({\alpha^{\prime}}^{2}\), обусловленный преобразованием от \(U\) к \(u\), не равен нулю при конечном \(u\). Однако при \(u\rightarrow\infty\), \(\alpha^{\prime}\to 0\) и вклад этого члена исчезает в этом пределе. Когда \(m=\text{constant}\), единственный существенный ненулевой член при \(u\rightarrow\infty\), таким образом, является терм Хокинга, который является постоянным и не зависит от процесса, приводящего к формированию черной дыры (т.е. не зависит от \(R(t)\)). Для конечного \(u\) это не так, и поток излучения, достигающий будущего нулевого бесконечности, чувствителен к процессу коллапса. Непонятно, соответствует ли это какой-либо полезной информации для асимптотического наблюдателя, поскольку в этом случае поверхности конечного \(u\) могут быть удалены в далекое прошлое за счет наложения друг на друга поверхностей постоянного \(u\) на горизонт событий. Теперь мы рассмотрим случай, когда \(\dot{m}\neq 0\). Как обсуждалось выше, источником излучения в этом случае ожидается поверхность \(r=r_{2m}\), которая смещена от глобального горизонта событий при \(r_{H}\). ### \(\mathbf{m\neq\text{константа}}\) Можно видеть, что когда \(\dot{m}\neq 0\), первые два слагаемых в (21) и (22), а также первое слагаемое в (23) все еще не зависят от процесса коллапса. Их форма изменяется относительно случая \(\dot{m}=0\), так как две функции \(A\) и \(B\) теперь заданы формулами (7) и (8), но по-прежнему стремятся к нулю при \(r\rightarrow\infty\). Когда \(\dot{m}\neq 0\), у нас появляются еще три новых слагаемых: третье слагаемое в (21) и (22) и второе слагаемое в (23). Эти слагаемые также исчезают при \(r\rightarrow\infty\), поэтому не вносят вклада в поток на будущей нулевой бесконечности². [FOOTNOTE:2][ENDFOOTNOTE] - [СНОСКА:2][КОНЕЦ_СНОСКИ] Единственными ненулевыми компонентами тензора энергии-импульса, при \(r\rightarrow\infty\), являются \[T_{uu}\rightarrow{\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))+F_{u}(\alpha ^{\prime}(u)).\] will be translated to Russian as: \[T_{uu} \rightarrow {\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))+F_{u}(\alpha ^{\prime}(u)).\] Это те же два члена, которые вносят вклад в асимптотический поток в случае \(\dot{m}=0\), но теперь члены \(\alpha\) и \(\beta\), а также преобразования координат между \(u\), \(U\) и \(t\), изменяются из-за не постоянного \(m(t)\). Подстановка (7), (8), (10) и (11) в выражение выше, вместе с соответствующими преобразованиями из \(u\) и \(U\) в \(t\), позволяет эти два члена оценить как функции \(t\). Из-за сложной формы полученных выражений мы выбираем не показывать их явно здесь, а представить их в виде графиков. Это продемонстрирует, как текущий случай отличается от случая \(m=\text{constant}\), которые мы будем отображать параллельно для сравнения. Для иллюстративных целей рассмотрим \(m=1-0.01t\) и \(R=2-0.6t\), так что \(R=r_{2m}\) при \(t=0\). Траектории \(R\), \(r_{2m}\) и \(r_{H}\) показаны на рисунке 2 соответственно сплошной линией, пунктирной линией и штриховой линией. До момента \(t=0\) оболочка находится вне обоих \(r_{2m}\) и \(r_{H}\). Между моментом \(t=0\) и \(t\simeq 0.13\) оболочка находится между \(r_{2m}\) и \(r_{H}\), а после \(t\simeq 0.13\) она находится внутри глобального горизонта. Мы будем называть этот выбор параметров "пустота 1". [ФИГУРА:S5.F2][КОНЕЦФИГУРЫ] \(F_{u}(\alpha^{\prime}(u))\) для отверстия 1 можно легко рассчитать и показано на рисунке 3(a) как функция \(t\) вдоль траектории \(R(t)\). Аналогично, \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) показано на рисунке 3(b). Эти графики были нормализованы таким образом, чтобы \(F_{u}(\alpha^{\prime}(u))=1\) при \(R=r_{H}\), момент пересечения оболочкой глобального горизонта событий. Для сравнения на рисунках 3(a) и 3(b) также показаны результаты, которые были бы получены для испаряющегося черной дыры с половинным темпом ("отверстие 2", пунктирные линии) и черной дыры с постоянной массой ("отверстие 3", штриховые линии). В обоих случаях траектория падающей оболочки остается такой же, как для отверстия 1, и оба были выбраны таким образом, чтобы \(r_{H}\) для всех трех отверстий было одинаковым в момент \(R=r_{H}\). [FIGURE:S5.F3][ENDFIGURE] - [ФИГУРА:S5.F3][КОНЕЦФИГУРЫ] Из рисунка 3 видно, что значение \(F_{u}(\alpha^{\prime}(u))\) для отверстия 3 примерно постоянно на рассматриваемом временном интервале, со скоростью Хокинга \(1/768\pi m^{2}\). Для отверстий 1 и 2 можно видеть, что \(F_{u}(\alpha^{\prime}(u))\) является медленно возрастающей функцией от \(t\), которая быстро возрастает при \(R\to r_{H}\). Значение \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) можно видеть приближается к нулю для всех трех отверстий при \(R\to r_{H}\), что ожидается. Это происходит из-за \({\alpha^{\prime}}(u)\to 0\) в этом пределе. Рассмотрим теперь, что измеряет наблюдатель на бесконечности. Чтобы найти это, мы должны преобразовать графики выше от \(t\) к \(t_{\infty}\), собственному времени асимптотического наблюдателя, с использованием \[dt_{\infty}=\left[A(t)\left(1-\sqrt{\frac{2m(t)}{R(t)}}-\dot{R}(t)\right) \right]dt.\] (24) Это выражение связывает две временные координаты через запаздывающее время \(u\). Два члена \(F_{u}(\alpha^{\prime}(u))\) и \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) теперь представлены в виде функции \(t_{\infty}\) на рисунках 4(a) и 4(b). Эти графики нормируются по значению \(F_{u}(\alpha^{\prime}(u))\) для отверстия 1 при \(R=r_{H}\), и новая временная координата для отверстий 1 и 2 выбрана так, чтобы \(t_{\infty}=0\), когда асимптотический наблюдатель видит \(R=r_{2m}\). (Это не возможно в статическом случае, так как поверхность \(r_{2m}\) является вырожденной с \(r_{H}\)). Единицы выбраны так, чтобы \(t_{\infty}=1\), когда асимптотический наблюдатель видит \(R=r_{H}\) в каждом случае. [FIGURE:S5.F4][ENDFIGURE] - [ФИГУРА:S5.F4][КОНЕЦ ФИГУРЫ] Эти графики идентичны тем, что изображены на рисунке 3, но они растянуты около \(R=r_{H}\) и сжаты около \(R=r_{2m}\), что дает им существенно отличающийся вид. Растяжение увеличивается по мере уменьшения скорости испарения и расходится в пределе статического отверстия. Поэтому линии, соответствующие отверстию 3, теперь являются прямыми и равны нулю в случае рисунка 4(b). Наблюдатель на бесконечности, наблюдающий отверстия 1 и 2, видит плотность энергии в режиме \(F_{u}(\alpha^{\prime}(u))\), которая возрастает, когда оболочка проходит через \(r_{2m}\), а затем увеличивается с постоянной скоростью. Это происходит из-за поверхностей, которые имеют постоянное значение \(u\) и накладываются на глобальный горизонт, растягивая шипы, видимые на рисунке 3(a). Увеличение излучения при пересечении оболочкой \(r_{2m}\) подтверждает предположение о том, что излучение происходит именно с этой поверхности, как было обнаружено в прямом расчете туннелирования. Фигура 4(b) показывает, что для отверстий 1 и 2 вклад от \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\), как наблюдается асимптотическим наблюдателем, становится экспоненциально малым вскоре после того, как оболочка пересекает \(r_{2m}\). Опять же, это связано с укладкой поверхностей, постоянных по \(u\), против глобального горизонта и растяжением рисунка 3(b). Однако вблизи \(R=r_{2m}\), хотя этот компонент мал, он все равно не равен нулю. Это интересно, так как известно, что \(F_{U}(\beta^{\prime}(U))\) чувствителен к процессу коллапса, приводящему к образованию отверстия [8]. Чтобы учесть степень, в которой исходящее излучение чувствительно к процессу коллапса, давайте сейчас незначительно изменим траекторию входящей оболочки на малую величину, так что \(R=3\times 10^{-5}\cos(10^{2}t)+2-0.6t\). Это достаточно незначительное возмущение, так что график траектории входящей оболочки неотличим от рисунка 2. Однако, эффекты на \(F_{u}(\alpha^{\prime}(u))\) и \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) не являются пренебрежимыми и показаны на рисунке 5. Такие возмущения траектории падения могут возникать из-за несовершенства сферической симметрии, внутренних напряжений или взаимодействия оболочки с другими объектами. Здесь мы просто хотим показать чувствительность излучения к процессу коллапса и добавить _ад хок_ осцилляцию к траектории оболочки. Было замечено, что такие осцилляции, хотя и малые, имеют заметное влияние на исходящее излучение черных дыр. Обе функции \(F_{u}(\alpha^{\prime}(u))\) и \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) можно видеть, осциллирующими вокруг своих невозмущенных значений, как показано на рисунке 3. Эти осцилляции особенно заметны в \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\). [ФИГУРА:S5.F5][КОНЕЦФИГУРЫ] Теперь давайте рассмотрим излучение, измеренное асимптотическим наблюдателем, наблюдающим изменение коллапса оболочки. Любые особенности, присутствующие на графиках на рисунке 5, также должны быть присутствовать в излучении, которое он/она измеряет, хотя оно будет подвержено растяжению и сжатию, связанным с преобразованием от \(t\) к \(t_{\infty}\). Используя (24), мы находим, что \(F_{u}(\alpha^{\prime}(u))\) и \({\alpha^{\prime}}^{2}(u)F_{U}(\beta^{\prime}(U))\) заданы как функции от \(t_{\infty}\), как показано на рисунке 6. Для отверстий 1 и 2 колебания, присутствовавшие на рисунке 5, снова являются очевидными, но теперь они ограничены наблюдением только вблизи \(R=r_{2m}\) (из-за наложения поверхностей постоянной \(u\) на глобальный горизонт). Бесконечное растяжение в случае отверстия 3 достаточно, чтобы удалить колебания, присутствовавшие на рисунке 5, в бесконечном прошлом. [РИСУНОК:S5.F6][КОНЕЦРИСУНКА] ## 6 Обсуждение Мы рассмотрели случай черной дыры, которая образуется в результате коллапса сферической оболочки и распадается через туннельные события. В этом случае параметр массы дыры становится функцией времени Панлеве, \(t\), а поверхность \(r=2m\) отделяется от глобального горизонта событий на небольшое расстояние. Туннельные события происходят при \(r=2m\), а не на глобальном горизонте событий. Это смещение оказывает влияние на излучение излучения Хокинга и его наблюдение асимптотическими наблюдателями, наблюдающими коллапс. Тензор энергии-импульса масселфес конформного скалярного поля получается в двумерном аналоге этого пространства-времени, и рассчитывается поток излучения, измеряемый асимптотическим наблюдателем. Асимптотический наблюдатель видит излучение, которое изначально возрастает примерно в момент, когда он видит, что коллапсирующая оболочка пересекает \(r=2m\), а затем увеличивается с постоянной скоростью. Это подтверждает идею того, что излучение Хокинга излучается из окрестности поверхности \(r=2m\) [16, 17, 18], и что после того, как эта поверхность становится доступной для асимптотических наблюдателей, он видит излучение от отверстия, температура которого медленно повышается. Излучение, исходящее извне глобального горизонта событий, содержит моды, чувствительные к процессу коллапса [8]. Эта чувствительность иллюстрируется путем возмущения коллапсирующей оболочки небольшой осцилляцией. Эффекты этого на моды, которые убегают в будущее нулевую бесконечность, ясно видны и исчезают только в пределе приближения к глобальному горизонту. В статической модели бесконечное наложение поверхностей постоянного отсроченного времени от глобального горизонта удаляет эти моды в далекое прошлое, так что неясно, имеют ли они какое-либо наблюдательное значение. Это не относится к нестатическим моделям. Здесь чувствительность излучения к процессу коллапса явно видна, но ограничена наблюдаемостью только в начале процесса испарения. Тем не менее, наблюдатель, который измеряет всё излучение из черной дыры, может в принципе извлечь некоторую информацию о процессе коллапса, который её сформировал. Есть несколько способов, с помощью которых можно улучшить данное исследование. В частности, можно параметризовать \(m\) как функцию от \(t\) более удовлетворительным способом. Здесь мы предполагаем функцию вида \(m=m_{0}+\dot{m}_{0}t\), чтобы получить явные, точные решения. Хотя это, вероятно, будет достоверно для ранних стадий испарения (являясь первым членом рядового разложения), в поздних стадиях это маловероятно будет хорошим приближением. Идеально было бы найти решения с более общей \(m(t)\). Дополнительной проблемой является поведение модели при \(m\to 0\), когда чёрная дыра полностью испаряется [10, 22]. В этом пределе (в зависимости от формы \(m(t)\)) связанные с пространство-временем скалярные кривизны (2) могут расходиться, указывая на сингулярность³. Это показывает, что предельное значение \(m(t)\) не является подходящим для непрерывного предела испарения и что следует ввести ограничение, после которого используется более соответствующий метод. [СНОСКА:3][КОНЕЦСНОСКИ] **Благодарности** Я благодарен Педро Феррейра и Филипу Канделасу за полезные обсуждения, а также Jesus College за поддержку. ## Ссылки * [1] С. У. Хокинг, Comm. Math. Phys. **43**, 199 (1975). * [2] М. К. Парих и Ф. Вилчек, Phys. Rev. Lett. **85**, 5042 (2000). * [3] П. Краус и Ф. Вилчек, Nucl. Phys. B **433**, 403 (1995). Е. Кески-Ваккури и П. Краус, Nucl. Phys. B **491**, 249 (1997). * [4] Дж. Линдси, Foundations of Physics **37**, 1181 (2007). * [5] Б. А. Браун и Дж. Линдси, arXiv:0710.2032 (2007). * [6] Б. А. Браун и Дж. Линдси, arXiv:0802.1660 (2008). * [7] Т. Вачаспати, Д. Стојковић и Л. М. Краус, Phys. Rev. D **76**, 024005 (2007). Т. Вачаспати и Д. Стојковић, Phys. Lett. B **663**, 107 (2008). * [8] П. К. Дейвис, Proc. R. Soc. Lond. **351**, 129 (1976). * [9] П. К. Дейвис и С. А. Фуллинг, Proc. R. Soc. Lond. **348**, 393 (1975). * [10] У. А. Хискок, Phys. Rev. D **23**, 2813 (1981). * [11] Р. Балбинот, Phys. Rev. D **33**, 1611 (1986). * [12] П. Панлеве, C. R. Acad. Sci. (Paris) **173**, 677 (1921). * [13] Б. Д. Чаудхури, Pramana **70**, 593 (2008). Е. Т. Ахмедов, В. Ахмедова и Д. Синглтон, Phys. Lett. B **642**, 124 (2006). Е. Т. Ахмедов, В. Ахмедова, Т. Пилинг и Д. Синглтон, Int. J. Mod. Phys. A **22**, 1705 (2007). В. Ахмедова, Т. Пилинг, А. де Гилл и Д. Синглтон, arXiv:0804.2289, (2008). Т. К. Накамура, arXiv:0706.2916 (2007). П. Митра, Phys. Lett. B **648**, 240 (2007). * [14] К. Сринивасан и Т. Падманабхан, Phys. Rev. D **60**, 24007 (1999). С. Хемминг и Е. Кески-Ваккури, Phys. Rev. D **64**, 044006 (2001). С. Шанкарнараянан, Т. Падманабхан и К. Сринивасан, Class. Quant. Grav. **19**, 2671 (2002). А. Дж. М. Медвед, Phys. Rev. D **66**, 124009 (2002). Е. К. Вагенес, Phys. Lett. B **559**, 65 (2003). Т. Падманабхан, Mod. Phys. Lett. A **19**, 2637 (2004). А. Дж. М. Медвед и Е. К. Вагенес, Mod. Phys. Lett. A **20**, 2449 (2005). М. Арзано, А. Дж. М. Медвед и Е. К. Варганес, JHEP **0509**, 037 (2005). К. К. Джанг, Х. Л. Ли, С. З. Янг и Д. Й. Чен, Mod. Phys. Lett. A **22**, 891 (2007). * [15] С. А. Хэйвуд, Phys. Rev. Lett. **96**, 031103 (2006). А. Б. Нильсен, arXiv:0711.0313 (2007). А. Б. Нильсен, arXiv:0804.4435 (2008). * [16] М. Виссер, Int. J. Mod. Phys. D **12**, 649 (2003). * [17] Р. Ди Крисченцо, М. Надалини, Л. Ванцо, С. Зербини и Г. Зокателли, arXiv:0707.4425 (2007). * [18] А. Б. Нильсен, arXiv:0802.3442 (2008). * [19] Л. Сасскинд, Л. Торлакус и Дж. Углум, Phys. Rev. D **48**, 3743 (1993). * [20] В. Фролов, П. Саттон и А. Зельников, Phys. Rev. D **61**, 024021 (1999). * [21] П. К. Дейвис, С. А. Фуллинг и У. Г. Унрух, Phys. Rev. D **13**, 2720 (1976). * [22] Т. П. Сингх и К. Ваз, Phys. Lett. B **481**, 74 (2000). Переведите markdown с английского на русский. Сохраните формулы:

# The role of the \(\Delta(1232)\)-resonance in covariant baryon chiral perturbation theory J. M. Alarcón PRISMA Cluster of Excellence, Johannes Gutenberg-Universität, Mainz D-55099, Germany Institut für Kernphysik, Johannes Gutenberg-Universität, Mainz D-55099, Germany [email protected] (Day Month Year; Day Month Year) ###### Abstract We stress, on theoretical and phenomenological grounds, the importance of the \(\Delta(1232)\)-resonance in a chiral effective field theory approach applied to the study of \(\pi N\) scattering. We show how its inclusion as a dynamical degree of freedom allow us to obtain reliably valuable information from \(\pi N\) scattering data. keywords: \(\Delta(1232)\) resonance; \(\pi N\) scattering; Baryon chiral perturbation theory; \(\pi N\) sigma term. PACS numbers: 13.75.Gx, 11.30.Rd, 12.39.Fe, 13.85.Dz ## 1 Introduction The role of the \(\Delta(1232)\)-resonance in baryon chiral perturbation theory (BChPT) has been an old and interesting topic since the beginning of the 90’s[1], and its importance is related to the proper formulation of the effective field theory. This is because the \(\Delta(1232)\) couples strongly to the \(\pi N\) system already at low energies, what translates into a strong influence of this resonance in the \(\pi N\) scattering process even at very low energies. This motivates, from the phenomenological point of view, the explicit inclusion of this resonance, since one can expect that it will play an important role as an active degree of freedom in an effective field theory of \(\pi N\) scattering. Through this inclusion, one keeps a proper separation of scales and can extend the range of validity of the perturbative treatment.[2] On the other hand, one can also justify this inclusion invoking large \(N_{c}\) limit arguments since, in the emerging spin-flavor symmetry, nucleons and deltas are part of the same mutliplet.[3] ## 2 Extending BChPT The possible ways to incorporate the \(\Delta(1232)\) in chiral effective field theory (EFT) have been the subject of intensive research. Some crucial questions that one must address are: 1) How to filter the unphysical degrees of freedom introduced by the Rarita-Schwinger (RS) field that represents the \(\Delta\), and 2) how to deal with the new scale \(m_{\Delta}\), i. e., redefine a counting that takes into account the mass splitting \(\delta=m_{\Delta}-m_{N}\). For the results that we will show here, we employed the consistent formulation of chiral Lagrangians[4] in combination with the \(\delta\)-counting.[4, 5] Another issue related to chiral effective field theory with baryons is how to keep explicitly Lorentz invariance in the formulation without breaking the standard chiral counting. Here we employ the extended-on-mass-shell scheme[6] (EOMS), which will be an important ingredient in the correct extraction of the \(\pi N\) scattering observables.[2] This allow us to overcome some problems that the Heavy Baryon (HBChPT) and Infrared Regularization (IR) formulations have in extracting some important information related to \(\pi N\) scattering phenomenology. In the following we will show how the inclusion of the \(\Delta\) in the EOMS renormalized BChPT allow us to exploit the theory to obtain valuable information directly from experimental data. This EOMS renormalized approach is what we call covariant BChPT. ## 3 \(\pi N\) scattering phenomenology In this section we summarize some important results obtained from the inclusion of the \(\Delta\) in covariant BChPT. The crucial improvement achieved by this approach is directly related to the convergence of the chiral series, which translates into an improved description of the physical and the subthreshold regions. Also, we obtained a better convergence in the chiral expansion of the extracted quantities related to \(\pi N\) scattering.[2] Such improved convergence is not observed, however, in the IR formulation[2, 7]. Notice that the lack of convergence in the subthreshold region in previous analyses questioned the applicability of BChPT to \(\pi N\) scattering.[8] In the following we concentrate in two practical applications of our calculation: The extraction of the pion-nucleon sigma term (\(\sigma_{\pi N}\)) from \(\pi N\) scattering data and its impact on the calculation of the strangeness content of the nucleon (\(\sigma_{s}\)). ### The pion-nucleon sigma term The pion-nucleon sigma term is a quantity that contains information about the internal scalar structure of the nucleon which is used in a broad variety of nuclear-physics calculations.[9, 10, 11] However, it has become more known due to its impact on estimations of direct detection of dark matter[12], since it is related to the scalar coupling of the nucleon: \[\sigma_{\pi N}=\frac{\hat{m}}{2m_{N}}\langle N|\bar{u}u+\bar{d}d| N\rangle,\hskip 56.905512pt\hat{m}=\frac{m_{u}+m_{d}}{2}.\] (1) Since this quantity has a direct impact on \(\pi N\) scattering, it is possible to extract it in a model-independent way from a BChPT calculation of this process. This has been already attempted in previous works, but the lack of convergence did not allow to give a reliable estimation of \(\sigma_{\pi N}\). However, this problem can be overcome in the covariant approach of BChPT including the \(\Delta\)-resonance.[2, 13] In this way one is able to extract a reliable value for \(\sigma_{\pi N}\) employing only experimental information. We report, from modern \(\pi N\) scattering data, a value of[2, 13] \[\sigma_{\pi N}=59(7)\text{~{}MeV.}\] (2) This result, on the other hand, is compatible with updated \(\pi N\)-scattering phenomenology and modern pionic atoms data[13], and also with a recent calculation based on \(N_{f}=2+1\) LQCD world data.[14] ### The strangeness content of the nucleon The value of \(\sigma_{\pi N}\) deduced from scattering data has a direct impact on the strangeness content of the nucleon, defined as \[\sigma_{s}\equiv\frac{m_{s}}{2m_{N}}\langle N|\bar{s}s|N\rangle,\] (3) since the deviation of \(\sigma_{\pi N}\) from the non-singlet contribution to the nucleon mass \[\sigma_{0}\equiv\frac{\hat{m}}{2m_{N}}\langle N|\bar{u}u+\bar{d}d -2\bar{s}s|N\rangle\] (4) is proportional to \(\sigma_{s}\).[15, 16] The calculation of \(\sigma_{s}\) through \(\sigma_{0}\) has the important advantage that the latter can be obtained from the octet mass splittings.[15] In fact, with this method Gasser extracted from the hadron spectrum a value of \(\sigma_{0}=35(5)\) MeV using a pre-ChPT model for the interaction of the baryon with the meson cloud.[15] On the other hand, a later calculation in \(SU(3)\) HBChPT obtained a value of \(\sigma_{0}=36(7)\) MeV.[17] However, it is important to take into account that HBChPT has a poor convergence in the \(SU(3)\) sector and also that the decuplet can play an important role in the final value of \(\sigma_{0}\).[18] Notice the importance of an accurate determination of this quantity in the final evaluation of \(\sigma_{s}\) through \(\sigma_{0}\).[16] For this reason, we updated the value of \(\sigma_{0}\) with a covariant BChPT calculation including the contribution of the decuplet. We obtained a result of [16] \[\sigma_{0}=58(8)~{}\text{MeV},\] (5) which implies, \[\sigma_{s}=16(80)~{}\text{MeV},\] (6) for a \(\sigma_{\pi N}=59(7)\) MeV. This result, obtained uniquely from experimental information, is in good agreement with the LQCD estimations for the strangeness in the nucleon, that also point to a small content.[19, 20] Such a good agreement is not obtained, however, from the classical value of \(\sigma_{\pi N}=45(8)\) MeV,[21] from where one obtains \(\sigma_{s}=-150(80)\) MeV.[16] ## 4 Summary and Conclusions Based on our analyses of \(\pi N\) scattering with and without the \(\Delta(1232)\) included explicitly as a degree of freedom in BChPT within the IR and EOMS schemes[2, 7], we analyzed which framework exploits better the possibilities of the theory to study the \(\pi N\)-scattering process. We found that, in order to achieve the best convergence properties, it is crucial to combine a consistent inclusion of the \(\Delta(1232)\) resonance together with a renormalization scheme that preserves the analytical properties of a covariant calculation (EOMS). Once this is done, the calculated chiral amplitude shows an improved convergence that allow us to extract reliably the \(\pi N\) scattering phenomenology at low energies and below the threshold.[2] This better convergence allowed us to solve previous disagreements with dispersive methods that questioned the applicability of BChPT to the study of \(\pi N\) scattering.[8] Also, as commented in Sec. 3, this improvement allowed us to extract reliably and accurately the value of \(\sigma_{\pi N}\) and \(\sigma_{s}\) employing only experimental information. These were found to be compatible with updated phenomenology[13] and recent LQCD determinations.[14, 19, 20] We can conclude then, that the inclusion of the \(\Delta(1232)\) resonance in covariant BChPT is very important to exploit the potential of chiral effective field theory with baryons. ## References * [1] E. E. Jenkins and A. V. Manohar, Phys. Lett. B **259**, 353 (1991). * [2] J. M. Alarcon, J. Martin Camalich and J. A. Oller, Ann. of Phys. 336 413-461 (2013). * [3] A. C. Cordon and J. L. Goity, Phys. Rev. D **87**, 016019 (2013). * [4] V. Pascalutsa and R. Timmermans, Phys. Rev. C **60**, 042201 (1999). * [5] C. Hanhart and N. Kaiser, Phys. Rev. C **66**, 054005 (2002). * [6] T. Fuchs, J. Gegelia, G. Japaridze and S. Scherer, Phys. Rev. D **68**, 056005 (2003). * [7] J. M. Alarcon, J. Martin Camalich, J. A. Oller and L. Alvarez-Ruso, Phys. Rev. C **83**, 055205 (2011). * [8] T. Becher and H. Leutwyler, JHEP **0106**, 017 (2001). * [9] K. Fukushima and C. Sasaki, Prog. Part. Nucl. Phys. **72**, 99 (2013). * [10] J. C. Berengut, E. Epelbaum, V. V. Flambaum, C. Hanhart, U.-G. Meißner, J. Nebreda and J. R. Pelaez, Phys. Rev. D **87**, 085018 (2013). E. Epelbaum, H. Krebs, T. A. Lähde, D. Lee and U.-G. Meißner, Eur. Phys. J. A **49**, 82 (2013). * [11] A. Lacour, J. A. Oller and U.-G. Meißner, J. Phys. G **37** 125002 (2010). * [12] A. Bottino, _et al._, Astropart. Phys. **13**, 215 (2000); Astropart. Phys. **18**, 205 (2002). J. R. Ellis, K. A. Olive and C. Savage, Phys. Rev. D **77**, 065026 (2008). * [13] J. M. Alarcon, J. Martin Camalich and J. A. Oller, Phys. Rev. D **85**, 051503 (2012). * [14] L. Alvarez-Ruso, T. Ledwig, J. Martin Camalich and M. J. Vicente-Vacas, Phys. Rev. D **88**, 054507 (2013). * [15] J. Gasser, Annals Phys. **136**, 62 (1981). * [16] J. M. Alarcon, L. S. Geng, J. Martin Camalich and J. A. Oller, arXiv:1209.2870. * [17] B. Borasoy and U. -G. Meissner, Annals Phys. **254**, 192 (1997). * [18] L. S. Geng, _et al._ Phys. Rev. Lett. **101**, 222002 (2008). * [19] H. Ohki _et al._, Phys. Rev. D **78**, 054502 (2008). * [20] P. Junnarkar and A. Walker-Loud, Phys. Rev. D **87**, 114510 (2013). * [21] J. Gasser, H. Leutwyler and M. E. Sainio, Phys. Lett. B **253**, 252 (1991).

# Роль резонанса \(\Delta(1232)\) в ковариантной пертурбационной хиральной теории барионов Переведите разметку с английского на русский. Сохраните формулы: J. M. Alarcón PRISMA Кластер превосходства, Иоганнес-Гутенберг-Университет, Майнц D-55099, Германия Институт ядерной физики, Иоганнес Гутенберг-Университет, Майнц, Германия, D-55099 Аларкон@kph.uni-mainz.de (День Месяц Год; День Месяц Год) ###### Аннотация Мы подчеркиваем важность резонанса \( \Delta(1232) \) с точки зрения теоретических и феноменологических основ в рамках эффективной хиральной теории поля, применяемой для изучения рассеяния \( \pi N \). Мы показываем, как его включение в качестве динамической степени свободы позволяет нам достоверно получать ценную информацию из данных о рассеянии \( \pi N \). Ключевые слова: \(\Delta(1232)\) резонанс; \(\pi N\) рассеяние; Барионная киральная теория возмущений; \(\pi N\) сигма-терм. Номера PACS: 13.75.Gx, 11.30.Rd, 12.39.Fe, 13.85.Dz. ## 1 Введение Роль резонанса \(\Delta(1232)\) в барионной хиральной теории возмущений (BChPT) является старой и интересной темой с начала 90-х годов[1], и её важность связана с правильной формулировкой эффективной полевой теории. Это связано с тем, что \(\Delta(1232)\) сильно связан с системой \(\pi N\) уже при низких энергиях, что приводит к сильному влиянию этого резонанса на процесс рассеяния \(\pi N\) даже при очень низких энергиях. С феноменологической точки зрения это мотивирует явное включение этого резонанса, поскольку можно ожидать, что он будет играть важную роль в качестве активной степени свободы в эффективной полевой теории рассеяния \(\pi N\). Через это включение можно сохранить правильную разделенность масштабов и расширить область применимости возмущенного подхода.[2] С другой стороны, это включение также можно обосновать с помощью аргументов большого предела \(N_c\), поскольку в возникающей спиново-флаворной симметрии нуклоны и дельты являются частью одного и того же мультиплета.[3] ## 2 Расширение Векторной ЧПТ Возможные способы включения \(\Delta(1232)\) в эффективную хиральную теорию сильных взаимодействий (EFT) являются предметом интенсивного исследования. Некоторые важные вопросы, которые необходимо рассмотреть, включают: 1) Как отфильтровать физически несоответствующие степени свободы, введенные полем Рарита-Швингера (RS), представляющим \(\Delta\), и 2) как работать с новой шкалой \(m_{\Delta}\), то есть переопределить подсчет, учитывающий разность масс \(\delta=m_{\Delta}-m_{N}\). В наших результатах, мы использовали последовательную формулировку хиральных лагранжианов[4] в сочетании с \(\delta\)-подсчетом.[4, 5] Другой вопрос, связанный с эффективной хиральной теорией с барионами, заключается в том, как сохранить явную инвариантность Лоренца в формулировке без нарушения стандартного хирального подсчета. Здесь мы используем расширенную схему на массовой оболочке[6] (EOMS), которая будет важным ингредиентом в правильном извлечении наблюдаемых величин рассеяния \(\pi N\).[2] Это позволяет нам преодолеть некоторые проблемы, с которыми сталкиваются тяжелые барионы (HBChPT) и регуляризация в инфракрасной области (IR) при извлечении некоторой важной информации, связанной с феноменологией рассеяния \(\pi N\). В следующем разделе мы покажем, как включение \(\Delta\) в ЭОСМ-ренормализованную BChPT позволяет нам использовать теорию для получения ценной информации непосредственно из экспериментальных данных. Этот подход с ренормализацией в ЭОСМ является тем, что мы называем ковариантной BChPT. ## Феноменология рассеяния \(3 \pi N\) В этом разделе мы подводим итоги некоторых важных результатов, полученных в результате включения \(\Delta\) в ковариантное BChPT. Решающим улучшением, достигнутым при данном подходе, является прямая связь сходимости кирального ряда, что приводит к улучшенному описанию физической области и субтрешхолдных областей. Также мы получили лучшую сходимость в киральном разложении извлеченных величин, связанных со \(\pi N\) рассеянием.[2] Однако такая улучшенная сходимость не наблюдается в ИК-формулировке[2, 7]. Следует отметить, что отсутствие сходимости в субтрешхолдной области в предыдущих анализах подвергает сомнению применимость BChPT к \(\pi N\) рассеянию.[8] В следующем мы сосредоточимся на двух практических применениях наших вычислений: извлечение сигма-терма пион-нуклон (\(\sigma_{\pi N}\)) из \(\pi N\) рассеяния данных и его влияние на вычисление странности содержания нуклона (\(\sigma_{s}\)). ### Массовый терм пион-нуклонного сигма Терм-сигма пион-нуклеон является величиной, которая содержит информацию о внутренней скалярной структуре нуклеона, используемую в широком спектре ядерно-физических расчетов[9, 10, 11]. Однако он стал более известен благодаря своему влиянию на оценки непосредственного обнаружения темной материи[12], так как он связан со скалярной связью нуклеона: \[\sigma_{\pi N}=\frac{\hat{m}}{2m_{N}}\langle N|\bar{u}u+\bar{d}d| N\rangle,\hskip 56.905512pt\hat{m}=\frac{m_{u}+m_{d}}{2}.\] (1) Поскольку эта величина непосредственно влияет на рассеяние \(\pi N\), ее можно извлечь в модельно-независимом виде из расчета этого процесса в рамках BChPT. Это уже пытались сделать в предыдущих работах, но недостаточная сходимость не позволяла получить надежную оценку для \(\sigma_{\pi N}\). Однако эту проблему можно преодолеть в ковариантном подходе BChPT с учетом \(\Delta\)-резонанса.[2, 13] Таким образом, можно получить надежное значение для \(\sigma_{\pi N}\), используя только экспериментальную информацию. Мы сообщаем значение для \(\sigma_{\pi N}\) на основе современных данных о рассеянии \(\pi N\)[2, 13]. \[\sigma_{\pi N}=59(7)\text{~{}МэВ.}\] (2) Этот результат, с другой стороны, согласуется с обновленной феноменологией рассеяния \(\pi N\) и современными данными по пионным атомам[13], а также с недавними расчетами на основе мировых данных LQCD с \(N_{f}=2+1\)[14]. ### Содержание странности нуклеона Значение \(\sigma_{\pi N}\), выведенное из данных о рассеянии, непосредственно влияет на содержание странности нуклона, определенное как \[\sigma_{s}\equiv\frac{m_{s}}{2m_{N}}\langle N|\bar{s}s|N\rangle,\] (3) \[\sigma_{s}\equiv\frac{m_{s}}{2m_{N}}\langle N|\bar{s}s|N\rangle,\] (3) так как отклонение \(\sigma_{\pi N}\) от не-синглетного вклада в массу нуклона \[\sigma_{0}\equiv\frac{\hat{m}}{2m_{N}}\langle N|\bar{u}u+\bar{d}d -2\bar{s}s|N\rangle\] (4) translates to: \[\sigma_{0}\equiv\frac{\hat{m}}{2m_{N}}\langle N|\bar{u}u+\bar{d}d -2\bar{s}s|N\rangle\] (4) пропорционален \(\sigma_{s}\).[15, 16] Расчет \(\sigma_{s}\) через \(\sigma_{0}\) имеет важное преимущество, поскольку последний можно получить из разделения масс октета.[15] Фактически, с помощью этого метода Гассер получил из спектра адронов значение \(\sigma_{0}=35(5)\) МэВ, используя предварительную модель пред-ХПТ для взаимодействия бариона с мезонным облаком.[15] С другой стороны, более поздний расчет в \(SU(3)\) HBХПТ получил значение \(\sigma_{0}=36(7)\) МэВ.[17] Однако важно учитывать, что HBХПТ имеет плохую сходимость в секторе \(SU(3)\), а также то, что децимплет может сыграть важную роль в конечном значении \(\sigma_{0}\).[18] Заметьте важность точного определения этой величины в конечной оценке \(\sigma_{s}\) через \(\sigma_{0}\).[16] По этой причине мы обновили значение \(\sigma_{0}\) с помощью ковариантного расчета ВХПТ с учетом вклада децимплета. Мы получили результат [16] \[\sigma_{0}=58(8)~{}\text{МэВ},\] (5) что это подразумевает, \[\sigma_{s}=16(80)~{}\text{MeV},\] (6) \[\sigma_{s}=16(80)~{}\text{МэВ},\] (6) для \( \sigma_{\pi N}=59(7) \) МэВ. Этот результат, полученный исключительно на основе экспериментальной информации, хорошо соответствует оценкам LQCD для странности в нуклоне, которые также указывают на небольшое содержание.[19, 20] Однако такого хорошего согласия не достигается при классическом значении \( \sigma_{\pi N}=45(8) \) МэВ,[21] откуда получается \( \sigma_{s}=-150(80) \) МэВ.[16] ## 4 Резюме и Выводы На основе наших анализов рассеяния \( \pi N \) с и без \(\Delta(1232)\), включенной явно как степень свободы в рамках BChPT в непрерывной и схеме EOMS[2, 7], мы проанализировали, какая из рамок лучше использует возможности теории для изучения процесса \( \pi N \)-рассеяния. Мы обнаружили, что для достижения лучших свойств сходимости критически важно сочетать последовательное включение резонанса \( \Delta(1232) \) с долговременной схемой ренормализации, которая сохраняет аналитические свойства ковариантных вычислений (EOMS). После выполнения этого расчетного хиральный амплитуда показывает улучшенную сходимость, позволяющую надежно извлекать феноменологию рассеяния \( \pi N \) при низких энергиях и ниже порога.[2] Это лучшая сходимость позволила нам разрешить предыдущие разногласия с дисперсионными методами, которые ставили под сомнение применимость BChPT к изучению рассеяния \( \pi N \)[8]. Кроме того, как указано в разделе 3, это улучшение позволило нам надежно и точно извлечь значение \( \sigma_{\pi N} \) и \( \sigma_s \), используя только экспериментальную информацию. Они оказались совместимы с обновленной феноменологией[13] и последними определениями на LQCD[14, 19, 20]. Мы можем сделать вывод, что включение резонанса \( \Delta(1232) \) в ковариантную BChPT является очень важным для использования потенциала кирального эффективного поля с барионами. ## Ссылки * [1] E. E. Jenkins and A. V. Manohar, Phys. Lett. B **259**, 353 (1991). * [2] J. M. Alarcon, J. Martin Camalich and J. A. Oller, Ann. of Phys. 336 413-461 (2013). * [3] A. C. Cordon and J. L. Goity, Phys. Rev. D **87**, 016019 (2013). * [4] V. Pascalutsa and R. Timmermans, Phys. Rev. C **60**, 042201 (1999). * [5] C. Hanhart and N. Kaiser, Phys. Rev. C **66**, 054005 (2002). * [6] T. Fuchs, J. Gegelia, G. Japaridze and S. Scherer, Phys. Rev. D **68**, 056005 (2003). * [7] J. M. Alarcon, J. Martin Camalich, J. A. Oller and L. Alvarez-Ruso, Phys. Rev. C **83**, 055205 (2011). * [8] T. Becher and H. Leutwyler, JHEP **0106**, 017 (2001). * [9] K. Fukushima and C. Sasaki, Prog. Part. Nucl. Phys. **72**, 99 (2013). * [10] J. C. Berengut, E. Epelbaum, V. V. Flambaum, C. Hanhart, U.-G. Meißner, J. Nebreda and J. R. Pelaez, Phys. Rev. D **87**, 085018 (2013). E. Epelbaum, H. Krebs, T. A. Lähde, D. Lee and U.-G. Meißner, Eur. Phys. J. A **49**, 82 (2013). * [11] A. Lacour, J. A. Oller and U.-G. Meißner, J. Phys. G **37** 125002 (2010). * [12] A. Bottino, _et al._, Astropart. Phys. **13**, 215 (2000); Astropart. Phys. **18**, 205 (2002). J. R. Ellis, K. A. Olive and C. Savage, Phys. Rev. D **77**, 065026 (2008). * [13] J. M. Alarcon, J. Martin Camalich and J. A. Oller, Phys. Rev. D **85**, 051503 (2012). * [14] L. Alvarez-Ruso, T. Ledwig, J. Martin Camalich and M. J. Vicente-Vacas, Phys. Rev. D **88**, 054507 (2013). * [15] J. Gasser, Annals Phys. **136**, 62 (1981). * [16] J. M. Alarcon, L. S. Geng, J. Martin Camalich and J. A. Oller, arXiv:1209.2870. * [17] B. Borasoy and U. -G. Meissner, Annals Phys. **254**, 192 (1997). * [18] L. S. Geng, _et al._ Phys. Rev. Lett. **101**, 222002 (2008). * [19] H. Ohki _et al._, Phys. Rev. D **78**, 054502 (2008). * [20] P. Junnarkar and A. Walker-Loud, Phys. Rev. D **87**, 114510 (2013). * [21] J. Gasser, H. Leutwyler and M. E. Sainio, Phys. Lett. B **253**, 252 (1991). Перевод маркдауна с английского на русский. Сохранение формул:

# Evolutionary Stochastic Search for Bayesian model exploration Leonardo Bottolo Institute for Mathematical Sciences, Imperial College London, UK [email protected] Sylvia Richardson Centre for Biostatistics, Imperial College, London, UK [email protected] Address for correspondence: Sylvia Richardson, Department of Epidemiology and Public Health, Imperial College, 1 Norfolk Place, London, W2 1PG, UK. ###### Abstract Implementing Bayesian variable selection for linear Gaussian regression models for analysing high dimensional data sets is of current interest in many fields. In order to make such analysis operational, we propose a new sampling algorithm based upon Evolutionary Monte Carlo and designed to work under the “large \(p\), small \(n\)” paradigm, thus making fully Bayesian multivariate analysis feasible, for example, in genetics/genomics experiments. Two real data examples in genomics are presented, demonstrating the performance of the algorithm in a space of up to \(10,000\) covariates. Finally the methodology is compared with a recently proposed search algorithms in an extensive simulation study. _Keywords_: Evolutionary Monte Carlo; Fast Scan Metropolis-Hastings schemes; Linear Gaussian regression models; Variable selection. ## 1 Introduction This paper is a contribution to the methodology of Bayesian variable selection for linear Gaussian regression models, an important problem which has been much discussed both from a theoretical and a practical perspective (see Chipman _et al._, 2001 and Clyde and George, 2004 for literature reviews). Recent advances have been made in two directions, unravelling the theoretical properties of different choices of prior structure for the regression coefficients (Fernández _et al._, 2001; Liang _et al._, 2008) and proposing algorithms that can explore the huge model space consisting of all the possible subsets when there are a large number of covariates, using either MCMC or other search algorithms (Kohn _et al._, 2001; Dellaportas _et al._, 2002; Hans _et al._, 2007). In this paper, we propose a new sampling algorithm for implementing the variable selection model, based on tailoring ideas from Evolutionary Monte Carlo (Liang and Wong, 2000; Jasra _et al._, 2007; Wilson _et al._, 2009) in order to overcome the known difficulties that MCMC samplers face in a high dimension multimodal model space: enumerating the model space becomes rapidly unfeasible even for a moderate number of covariates. For a Bayesian approach to be operational, it needs to be accompanied by an algorithm that samples the indicators of the selected subsets of covariates, together with any other parameters that have not been integrated out. Our new algorithm for searching through the model space has many generic features that are of interest _per se_ and can be easily coupled with any prior formulation for the variance-covariance of the regression coefficients. We illustrate this by implementing \(g\)-priors for the regression coefficients as well as independent priors: in both cases the formulation we adopt is general and allows the specification of a further level of hierarchy on the priors for the regression coefficients, if so desired. The paper is structured as follows. In Section 2, we present the background of Bayesian variable selection, reviewing briefly alternative prior specifications for the regression coefficients, namely \(g\)-priors and independent priors. Section 3 is devoted to the description of our MCMC sampler which uses a wide portfolio of moves, including two proposed new ones. Section 4 demonstrates the good performance of our new MCMC algorithm in a variety of real and simulated examples with different structures on the predictors. In Section 4.2 we complement the results of the simulation study by comparing our algorithm with the recent Shotgun Stochastic Search algorithm of Hans _et al._ (2007). Finally Section 5 contains some concluding remarks. ## 2 Background ### Variable selection Let \(y=\left(y_{1},\ldots,y_{n}\right)^{T}\) be a sequence of \(n\) observed responses and \(x_{i}=\left(x_{i1},\ldots,x_{ip}\right)^{T}\) a vector of predictors for \(y_{i}\), \(i=1,\ldots,n\), of dimension \(p\times 1\). Moreover let \(X\) be the \(n\times p\) design matrix with \(i\)th row \(x_{i}^{T}\). A Gaussian linear model can be described by the equation \[y=\alpha 1_{n}+X\beta+\varepsilon,\] where \(\alpha\) is an unknown constant, \(1_{n}\) is a column vector of ones, \(\beta=\left(\beta_{1},\ldots,\beta_{p}\right)^{T}\) is a \(p\times 1\) vector of unknown parameters and \(\varepsilon\sim N\left(0,\sigma^{2}I_{n}\right)\). Suppose one wants to model the relationship between \(y\) and a subset of \(x_{1},\ldots,x_{p}\), but there is uncertainty about which subset to use. Following the usual convention of only considering models that have the intercept \(\alpha\), this problem, known as variable selection or subset selection, is particularly interesting when \(p\) is large and parsimonious models containing only a few predictors are sought to gain interpretability. From a Bayesian perspective the problem is tackled by placing a constant prior density on \(\alpha\) and a prior on \(\beta\) which depends on a latent binary vector \(\gamma=\left(\gamma_{1},\ldots,\gamma_{p}\right)^{T}\), where \(\gamma_{j}=1\) if \(\beta_{j}\neq 0\) and \(\gamma_{j}=0\) if \(\beta_{j}=0\), \(j=1,\ldots,p\). The overall number of possible models defined through \(\gamma\) grows exponentially with \(p\) and selecting the best model that predicts \(y\) is equivalent to find one over the \(2^{p}\) subsets that form the model space. Given the latent variable \(\gamma\), a Gaussian linear model can therefore be written as \[y=\alpha 1_{n}+X_{\gamma}\beta_{\gamma}+\varepsilon,\] (1) where \(\beta_{\gamma}\) is the non-zero vector of coefficients extracted from \(\beta\), \(X_{\gamma}\) is the design matrix of dimension \(n\times p_{\gamma}\), \(p_{\gamma}\equiv\gamma^{T}1_{p}\), with columns corresponding to \(\gamma_{j}=1\). We will assume that, apart from the intercept \(\alpha\), \(x_{1},\ldots,x_{p}\) contains no variables that would be included in every possible model and that the columns of the design matrix have all been centred with mean \(0\). It is recommended to treat the intercept separately and assign it a constant prior: \(p\left(\alpha\right)\propto 1\), Fernández _et al._ (2001). When coupled with the latent variable \(\gamma\), the conjugate prior structure of \(\left(\beta_{\gamma},\sigma^{2}\right)\) follows a normal-inverse-gamma distribution \[p\left(\beta_{\gamma}\left|\gamma,\sigma^{2}\right.\right)=N\left(m_{\gamma}, \sigma^{2}\Sigma_{\gamma}\right)\] (2) \[p\left(\sigma^{2}\left|\gamma\right.\right)=p\left(\sigma^{2}\right)=InvGa \left(a_{\sigma},b_{\sigma}\right)\] (3) with \(a_{\sigma},b_{\sigma}>0\). Some guidelines on how to fix the value of the hyperparameters \(a_{\sigma}\) and \(b_{\sigma}\) are provided in Kohn _et al._ (2001), while the case \(a_{\sigma}=b_{\sigma}=0\) corresponds to the Jeffreys’ prior for the error variance, \(p\left(\sigma^{2}\right)\propto\sigma^{-2}\). Taking into account (1), (2), (3) and the prior specification for \(\alpha\), the joint distribution of all the variables (based on further conditional independence conditions) can be written as \[p\left(y,\gamma,\alpha,\beta_{\gamma},\sigma^{2}\right)=p\left(y\left|\gamma, \alpha,\beta_{\gamma},\sigma^{2}\right.\right)p\left(\alpha\right)p\left(\beta _{\gamma}\left|\gamma,\sigma^{2}\right.\right)p\left(\sigma^{2}\right)p\left( \gamma\right).\] (4) The main advantage of the conjugate structure (2) and (3) is the analytical tractability of the marginal likelihood whatever the specification of the prior covariance matrix \(\Sigma_{\gamma}\): \[\int p\left(y\left|\gamma,\alpha,\beta_{\gamma},\sigma^{2}\right. \right)p\left(\alpha\right)p\left(\beta_{\gamma}\left|\gamma,\sigma^{2}\right. \right)p\left(\sigma^{2}\right)d\alpha\text{\/{}\/}d\beta_{\gamma}d\sigma^{2}\] (5) \[\propto \left|X_{\gamma}^{T}X_{\gamma}+\Sigma_{\gamma}^{-1}\right|^{-1/2} \left|\Sigma_{\gamma}\right|^{-1/2}\left(2b_{\sigma}+S\left(\gamma\right) \right)^{-\left(2a_{\sigma}+n-1\right)/2},\] where \(S\left(\gamma\right)=C-M^{T}K_{\gamma}^{-1}M\), with \(C=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)+m_{\gamma}^{T} \Sigma_{\gamma}^{-1}m_{\gamma}\), \(M=X_{\gamma}^{T}\left(y-\bar{y}_{n}\right)+\Sigma_{\gamma}^{-1}m_{\gamma}\) and \(K_{\gamma}=X_{\gamma}^{T}X_{\gamma}+\Sigma_{\gamma}^{-1}\) (Brown _et al._, 1998). While the mean of the prior (2) is usually set equal to zero, \(m_{\gamma}=0\), a neutral choice (Chipman _et al._, 2001; Clyde and George, 2004), the specification of the prior covariance \(\Sigma_{\gamma}\) matrix leads to at least two different classes of priors: * •When \(\Sigma_{\gamma}=gV_{\gamma}\), where \(g\) is a scalar and \(V_{\gamma}=\left(X_{\gamma}^{T}X_{\gamma}\right)^{-1}\), it replicates the covariance structure of the likelihood giving rise to so called \(g\)-priors first proposed by Zellner (1986). * •When \(\Sigma_{\gamma}=cV_{\gamma}\), but \(V_{\gamma}=I_{p_{\gamma}}\) the components of \(\beta_{\gamma}\) are conditionally independent and the posterior covariance matrix is driven towards the independence case. We will adopt the notation \(\Sigma_{\gamma}=\tau V_{\gamma}\) as we want to cover both prior specification in a unified manner. Thus in the \(g\)-prior case, \(\Sigma_{\gamma}=\tau\left(X_{\gamma}^{T}X_{\gamma}\right)^{-1}\) while in the independent case, \(\Sigma_{\gamma}=\tau I_{p_{\gamma}}\). We will refer to \(\tau\) as the _variable selection coefficient_ for reasons that will become clear in the next Section. To complete the prior specification in (4), \(p\left(\gamma\right)\) must be defined. A complete discussion about alternative priors on the model space can be found in Chipman (1996) and Chipman _et al._ (2001). Here we adopt the beta-binomial prior illustrated in Kohn _et al._ (2001) \[p\left(\gamma\right)=\int p\left(\gamma\left|\omega\right.\right)p\left(\omega \right)d\omega=\frac{B\left(p_{\gamma}+a_{\omega},p-p_{\gamma}+b_{\omega} \right)}{B\left(a_{\omega},b_{\omega}\right)}\] (6) with \(p_{\gamma}\equiv\gamma^{T}1_{p}\), where the choice \(p\left(\gamma\left|\omega\right.\right)=\omega^{p_{\gamma}}\left(1-\omega \right)^{p-p_{\gamma}}\) implicitly induces a binomial prior distribution over the model size and \(p\left(\omega\right)=\omega^{a_{\omega}-1}\left(1-\omega\right)^{b_{\omega}-1} /B\left(a_{\omega},b_{\omega}\right)\). The hypercoefficients \(a_{\omega}\) and \(b_{\omega}\) can be chosen once \(E\left(p_{\gamma}\right)\) and \(V\left(p_{\gamma}\right)\) have been elicited. In the “large \(p\), small \(n\)” framework, to ensure sparse regression models where \(p_{\gamma}\ll p\), it is recommended to centre the prior for the model size away from the number of observations. ### Priors for the variable selection coefficient \(\tau\) #### 2.2.1 \(g\)-priors It is a known fact that \(g\)-priors have two attractive properties. Firstly they possess an automatic scaling feature (Chipman _et al._, 2001; Kohn _et al._, 2001). In contrast, for independent priors, the effect of \(V_{\gamma}=I_{p_{\gamma}}\) on the posterior distribution depends on the relative scale of \(X\) and standardisation of the design matrix to units of standard deviation is recommended. However, this is not always the best procedure when \(X\) is possibly skewed, or when the columns of \(X\) are not defined on a common scale of measurement. The second feature that makes \(g\)-priors particularly appealing is the rather simple structure of the marginal likelihood (5) with respect to the constant \(\tau\) which becomes \[\propto\left(1+\tau\right)^{-p_{\gamma}/2}\left(2b_{\sigma}+S\left(\gamma \right)\right)^{-\left(2a_{\sigma}+n-1\right)/2},\] (7) where, if \(m_{\gamma}=0\), \(S\left(\gamma\right)=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)- \frac{\tau}{1+\tau}\left(y-\bar{y}_{n}\right)^{T}X_{\gamma}\left(X_{\gamma}^{T }X_{\gamma}\right)^{-1}X_{\gamma}^{T}\left(y-\bar{y}_{n}\right)\). For computational reasons explained in the next Section, we assume that (7) is always defined: since we calculate \(S\left(\gamma\right)\) using the QR-decomposition of the regression \(\left(X_{\gamma},y-\bar{y}_{n}\right)\) (Brown _et al._, 1998), when \(n\leq p_{\gamma}\), \(S\left(\gamma\right)=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)/ \left(1+\tau\right)\). Despite the simplicity of (7), the choice of the constant \(\tau\) for \(g\)-priors is complex, see Fernández _et al._ (2001), Cui and George (2008) and Liang _et al._ (2008). Historically the first attempt to build a comprehensive Bayesian analysis placing a prior distribution on \(\tau\) dates back to Zellner and Siow (1980), where the data adaptivity of the degree of shrinkage adapts to different scenarios better than assuming standard fixed values. Zellner-Siow priors, Z-S hereafter, can be thought as a mixture of \(g\)-priors and an inverse-gamma prior on \(\tau\), \(\tau\sim InvGa(1/2,n/2)\), leading to \[p\left(\beta_{\gamma}\left|\gamma,\sigma^{2}\right.\right)\propto\int N\left(0 ,\sigma^{2}\tau\left(X_{\gamma}^{T}X_{\gamma}\right)^{-1}\right)p\left(\tau \right)d\tau.\] (8) Liang _et al._ (2008) analyse in details Z-S priors pointing out a variety of theoretical properties. From a computational point of view, with Z-S priors, the marginal likelihood \(p\left(y\left|\gamma\right.\right)=\int p\left(y\left|\gamma,\tau\right.\right )p\left(\tau\right)d\tau\) is no more available in closed form, something which is advantageous in order to quickly perform a stochastic search (Chipman _et al._, 2001). Even though Z-S priors need no calibration and the Laplace approximation can be derived (Tierney and Kadane, 1986), see Appendix A.2, never became as popular as \(g\)-priors with a suitable constant value for \(\tau\). For alternative priors, see also Cui and George (2008) and Liang _et al._ (2008). #### 2.2.2 Independent priors When all the variables are defined on the same scale, independent priors represent an attractive alternative to \(g\)-priors. The likelihood marginalised over \(\alpha\), \(\beta_{\gamma}\) and \(\sigma^{2}\) becomes \[p\left(y\left|\gamma\right.\right)\propto\tau^{-p_{\gamma}/2} \left|X_{\gamma}^{T}X_{\gamma}+\tau I_{p_{\gamma}}\right|^{-1/2}\left(2b_{ \sigma}+S\left(\gamma\right)\right)^{-\left(2a_{\sigma}+n-1\right)/2},\] (9) where, if \(m_{\gamma}=0\), \(S\left(\gamma\right)=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)- \left(y-\bar{y}_{n}\right)^{T}X_{\gamma}\left(X_{\gamma}^{T}X_{\gamma}+\tau I_ {p_{\gamma}}\right)^{-1}X_{\gamma}^{T}\left(y-\bar{y}_{n}\right)\). Note that (9) is computationally more demanding than (7) due to the extra determinant operator. Geweke (1996) suggests to fix a different value of \(\tau_{j}\), \(j=1,\ldots,p\), based on the idea of “substantially significant determinant” of \(\Delta X_{j}\) with respect to \(\Delta y\). However it is common practice to standardise the predictor variables, taking \(\tau=1\) in order to place appropriate prior mass on reasonable values of the regression coefficients (Hans _et al._, 2007). Another approach, illustrated in Bae and Mallick (2004), places a prior distribution on \(\tau_{j}\) without standardising the predictors. Regardless of the prior specification for \(\tau\), using the QR-decomposition on a suitable transformation of \(X_{\gamma}\) and \(y-\bar{y}_{n}\), the marginal likelihood (9) is always defined. ## 3 MCMC sampler In this Section we propose a new sampling algorithm that overcomes the known difficulties faced by MCMC schemes when attempting to sample a high dimension multimodal space. We discuss in a unified manner the general case where a hyperprior on the variable selection coefficient \(\tau\) is specified. This encompasses the \(g\)-prior and independent prior structure as well as the case of fixed \(\tau\) if a point mass prior is used. The multimodality of the model space is a known issue in variable selection and several ways to tackle this problem have been proposed in the past few years. Liang and Wong (2000) suggest an extension of parallel tempering called Evolutionary Monte Carlo, EMC hereafter, Nott and Green, N&G hereafter, (2004) introduce a sampling scheme inspired by the Swendsen-Wang algorithm while Jasra _et al._ (2007) extend EMC methods to varying dimension algorithms. Finally Hans _et al._ (2007) propose when \(p>n\) a new stochastic search algorithm, SSS, to explore models that are in the same neighbourhood in order to quickly find the best combination of predictors. We propose to solve the issue related to the multimodality of model space (and the dependence between \(\gamma\) and \(\tau\)) along the lines of EMC, applying some suitable parallel tempering strategies directly on \(p\left(y\left|\gamma,\tau\right.\right)\). The basic idea of parallel tempering, PT hereafter, is to weaken the dependence of a function from its parameters by adding an extra one called “temperature”. Multiple Markov chains, called “population” of chains, are run in parallel, where a different temperature is attached to each chain, their state is tentatively swap at every sweep by a probabilistic mechanism and the latent binary vector \(\gamma\) of the non-heated chain is recorded. The different temperatures have the effect of flatting the likelihood. This ensures that the posterior distribution is not trapped in any local mode and that the algorithm mixes efficiently, since every chain constantly tries to transmit information about its state to the others. EMC extents this idea, encompassing the positive features of PT and genetic algorithms inside a MCMC scheme. Since \(\beta\) and \(\sigma^{2}\) are integrated out, only two parameters need to be sampled, namely the latent binary vector and the variable selection coefficient. In this set-up the full conditionals to be considered are \[\left[p\left(\gamma_{l}\left|\cdots\right.\right)\right]^{1/t_{l}}\propto\left [p\left(y\left|\gamma_{l},\tau\right.\right)\right]^{1/t_{l}}\left[p\left( \gamma_{l}\right)\right]^{1/t_{l}}\] (10) \[p\left(\tau\left|\cdots\right.\right)\propto\prod\nolimits_{l=1}^{L}\left[p \left(y\left|\gamma_{l},\tau\right.\right)\right]^{1/t_{l}}p\left(\tau\right),\] (11) where \(L\) is the number of chains in the the population and \(t_{l}\), \(1=t_{1}<t_{2}<\cdots<t_{L}\), is the temperature attached to the \(l\)th chain while the population \(\bm{\gamma}\) corresponds to a set of chains that are retained simultaneously. Conditions for convergence of EMC algorithms are well understood and illustrated for instance in Jasra _et al._ (2007). At each sweep of our algorithm, first the population \(\bm{\gamma}\) in (10) is updated using a variety of moves inspired by genetic algorithms: “local moves”, the ordinary Metropolis-Hastings or Gibbs update on every chain; and “global moves” that include: i) selection of the chains to swap, based on some probabilistic measures of distance between them; ii) crossover operator, i.e. partial swap of the current state between different chains; iii) exchange operator, full state swap between chains. Both local and global moves are important although global moves are crucial because they allow the algorithm to jump from one local mode to another. At the end of the update of \(\bm{\gamma}\), \(\tau\) is then sampled using (11). The implementation of EMC that we propose in this paper includes several novel aspects: the use of a wide range of moves including two new ones, a local move, based on the Fast Scan Metropolis-Hastings sampler, particularly suitable when \(p\) is large and a bold global move that exploits the pattern of correlation of the predictors. Moreover, we developed an efficient scheme for tuning the temperature placement that capitalises the effective interchange between the chains. Another new feature is to use a Metropolis-within-Gibbs with adaptive proposal for updating \(\tau\), as the full conditional (11) is not available in closed form. ### EMC sampler for \(\bm{\gamma}\) In what follows, we will only sketch the rationale behind all the moves that we found useful to implement and discuss further the benefits of the new specific moves in Section 4.1. For the “large \(p\), small \(n\)” paradigm and complex predictor spaces, we believe that using a wide portfolio of moves is needed and offers better guarantee of mixing. From a notational point of view, we will use the double indexing \(\gamma_{l,j}\), \(l=1,\ldots,L\) and \(j=1,\ldots,p\) to denote the \(j\)th latent binary indicator in the \(l\)th chain. Moreover we indicate by \(\gamma_{l}=\left(\gamma_{l,1},\ldots,\gamma_{l,p}\right)^{T}\) the vector of binary indicators that characterise the state of the \(l\)th chain of the population \(\bm{\gamma}=\left(\gamma_{1},\ldots,\gamma_{L}\right)\). #### Local moves and Fast Scan Metropolis Hastings sampler Given \(\tau\), we first tried the simple MC\({}^{3}\) idea of Madigan and York (1995), also used by Brown _et al._ (1998) where add/delete and swap moves are used to update the latent binary vector \(\gamma_{l}\). For an add/delete move, one of the \(p\) variables is selected at random and if the latent binary value is \(0\) the proposed new value is \(1\) or _vice versa_. However, when \(p\gg p_{\gamma_{l}}\), where \(p_{\gamma_{l}}\) is the size of the current model for the \(l\)th chain, the number of sweeps required to select by chance a binary indicator with a value of \(1\) follows a geometric distribution with probability \(p_{\gamma}/p\) which is much smaller than \(1-p_{\gamma}/p\) to select a binary indicator with a value of \(0\). Hence, the algorithm spends most of the time trying to add rather than delete a variable. Note that this problem also affects RJ-type algorithms (Dellaportas _et al._, 2002). On the other hand, Gibbs sampling (George and McCulloch, G&McC hereafter, 1993) is not affected by this issue since the state of the \(l\)th chain is updated by sampling from \[\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}\propto\exp\left\{\left(\log p\left(y\left|\gamma_{l,j}^{\left(1 \right)},\tau\right.\right)+\log p\left(\gamma_{l,j}=1\left|\gamma_{l,j^{-}} \right.\right)\right)/t_{l}\right\},\] (12) where \(\gamma_{l,j^{-}}\) indicates for the \(l\)th chain all the variables, but the \(j\)th, \(j=1,\ldots,p\) and \(\gamma_{l,j}^{\left(1\right)}=\left(\gamma_{l,1},\ldots,\gamma_{l,j-1},\gamma_ {l,j}=1,\gamma_{l,j+1},\ldots,\gamma_{l,p}\right)^{T}\). The main problem related to Gibbs sampling is the large number of models it evaluates if a full Gibbs cycle or any permutation of the indices is implemented at each sweep. Each model requires the direct evaluation, or at least the update, of the time consuming quantity \(S\left(\gamma\right)\), equation (7) or (9), making practically impossible to rely solely on the Gibbs sampler when \(p\) is very large. However, as sharply noticed by Kohn _et al._ (2001), it is wasteful to evaluate all the \(p\) updates in a cycle because if \(p_{\gamma_{l}}\) is much smaller than \(p\) and given \(\gamma_{l,j}=0\), it is likely that the sampled value of \(\gamma_{l,j}\) is again \(0\). When \(p\) is large, we thus consider instead of the standard MC\({}^{3}\) add/delete, swap moves, a novel Fast Scan Metropolis-Hastings scheme, FSMH hereafter, specialised for EMC/PT. It is computationally less demanding than a full Gibbs sampling on all \(\gamma_{l,j}\) and do not suffer from the problem highlighted before for MC\({}^{3}\) and RJ-type algorithms when \(p\gg p_{\gamma_{l}}\). The idea behind the FSMH move is to use an additional acceptance/rejection step (which is very fast to evaluate) to choose the number of indices where to perform the Gibbs-like step: the novelty of our FSMH sampler is that the additional probability used in the acceptance/rejection step is based not only on the current chain model size \(p_{\gamma_{l}}\), but also on the temperature \(t_{l}\) attached to the \(l\)th chain. Therefore the aim is to save computational time in the large \(p\) set-up when multiple chains are simulated in parallel and finding an alternative scheme to a full Gibbs sampler. To save computational time our strategy is to evaluate the time consuming marginal likelihood (5) in no more than approximately \(\left\lfloor\tilde{\theta}_{l,\bullet}^{(1)}\left(1/t_{l}\right)\left(p-p_{ \gamma}\right)+\tilde{\theta}_{l,\bullet}^{(0)}\left(1/t_{l}\right)p_{\gamma}\right\rfloor\) times per cycle in the \(l\)th chain (assuming convergence is reached), where \(\tilde{\theta}_{l,\bullet}^{(1)}\left(1/t_{l}\right)\) is the probability to select a variable to be added in the acceptance/rejection step which depends on the current model size \(p_{\gamma_{l}}\) and the temperature \(t_{l}\) and similarly for \(\tilde{\theta}_{l,\bullet}^{(0)}\left(1/t_{l}\right)\) (\(\left\lfloor\cdot\right\rfloor\) indicates the integer part). Since for chains attached to lower temperatures \(\tilde{\theta}_{l,\bullet}^{(0)}\left(1/t_{l}\right)\gg\tilde{\theta}_{l, \bullet}^{(1)}\left(1/t_{l}\right)\), the algorithm proposes to update _almost all_ binary indicators with value \(1\), while it selects at random a group of approximately \(\left\lfloor\tilde{\theta}_{l,\bullet}^{(1)}\left(1/t_{l}\right)\left(p-p_{ \gamma}\right)\right\rfloor\) binary indicators with value 0 to be updated. At higher temperatures since \(\tilde{\theta}_{l,\bullet}^{(0)}\) and \(\tilde{\theta}_{l,\bullet}^{(1)}\) become more similar, the number of models evaluated in a cycle increases because much more binary indicators with value \(0\) are updated. Full details of the FSMH scheme is given in the Appendix A.1, while evaluation of them and comparison with MC\({}^{3}\) embedded in EMC are presented in Sections 4.1 and 4.2 #### Global move: crossover operator The first step of this move consists of selecting the pair of chains \(\left(l,r\right)\) to be operated on. We firstly compute a probability equal to the weight of the “Boltzmann probability”, \(p_{t}\left(\gamma_{l}\left|\tau\right.\right)=\exp\left\{f\left(\gamma_{l} \left|\tau\right.\right)/t\right\}/F_{t}\), where \(f\left(\gamma_{l}\left|\tau\right.\right)=\log p\left(\gamma_{l}\left|y,\tau \right.\right)+\log p\left(\gamma_{l}\right)\) is the log transformation of the full conditional (10) assuming \(t_{l}=1\)\(\forall l\), \(l=1,\ldots,L\), and \(F_{t}=\sum_{l=1}^{L}\exp\left\{f\left(\gamma_{l}\left|\tau\right.\right)/t\right\}\) for some specific temperature \(t\), and then rank all the chains according to this. We use normalised Boltzmann weights to increase the chance that the two selected chains will give rise, after the crossover, to a new configuration of the population with higher posterior probability. We refer to this first step as “selection operator”. Suppose that two new latent binary vectors are then generated from the selected chains according to some crossover operator described below. The new proposed population of chains \(\bm{\gamma}^{\prime}=\left(\gamma_{1},\ldots,\gamma_{l}^{\prime},\ldots,\gamma _{r}^{\prime},\ldots,\gamma_{L}\right)\) is accepted with probability \[\alpha\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\right)=\min\left\{1, \frac{\exp\left\{f\left(\gamma_{l}^{\prime}\left|\tau\right.\right)/t_{l}+f \left(\gamma_{r}^{\prime}\left|\tau\right.\right)/t_{r}\right\}}{\exp\left\{f \left(\gamma_{l}\left|\tau\right.\right)/t_{l}+f\left(\gamma_{r}\left|\tau \right.\right)/t_{r}\right\}}\frac{Q_{t}\left(\bm{\gamma}^{\prime}\to \bm{\gamma}\left|\tau\right.\right)}{Q_{t}\left(\bm{\gamma}\rightarrow\bm{ \gamma}^{\prime}\left|\tau\right.\right)}\right\},\] (13) where \(Q_{t}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\left|\tau\right.\right)\) is the proposal probability, see Liang and Wong (2000). In the following we will assume that four different crossover operators are selected at random at every EMC sweep: \(1\)-point crossover, uniform crossover, adaptive crossover (Liang and Wong, 2000) and a novel block crossover. Of these four moves, the uniform crossover which “shuffles” the binary indicators along all the selected chains is expected to have a low acceptance, but to be able to genuinely traverse regions of low posterior probability. The block crossover essentially tries to swap a group of variables that are highly correlated and can be seen as a multi-points crossover whose crossover points are not random but defined from the correlation structure of the covariates. In practice the block crossover is defined as follows: one variable is selected at random with probability \(1/p\), then the pairwise correlation \(\rho\left(X_{j},X_{j^{\prime}}\right)\) between the \(j\)th selected predictor and each of the remaining covariates, \(j^{\prime}=1,\ldots,p\), \(j^{\prime}\neq j\), is calculated. We then retain for the block crossover all the covariates with positive (negative) pairwise correlation with \(X_{j}\) such that \(\left|\rho\left(X_{j},X_{j^{\prime}}\right)\right|\geq\rho_{0}\). The threshold \(\rho_{0}\) is chosen with consideration to the specific problem, but we fixed it at \(0.25\). Evaluation of block crossover and comparisons with other crossover operators are presented on a real data example in Section 4.1. #### Global move: exchange operator The exchange operator can be seen as an extreme case of crossover operator, where the first proposed chain receives the whole second chain state \(\gamma_{l}^{\prime}=\gamma_{r}\), and _vice versa_. In order to achieve a good acceptance rate, the exchange operator is usually applied on adjacent chains in the temperature ladder, which limits its capacity for mixing. To obtain better mixing, we implemented two different approaches: the first one is based on Jasra _et al._ (2007) and the related idea of delayed rejection (Green and Mira, 2001); the second, a bolder “all-exchange” move, is based on a precalculation of all the \(L\left(L-1\right)/2\) exchange acceptance rates between all chains pairs (Calvo, 2005). Full relevant details are presented in Appendix A.1. Both of these bold moves perform well in the real data applications, see Section 4.1, and simulated examples, see Section 4.2, thus contributing to the efficiency of the algorithm. #### Temperature placement As noted by Goswami and Liu (2007), the placement of the temperature ladder is the most important ingredient in population based MCMC methods. We propose a procedure for the temperature placement which has the advantage of simplicity while preserving good accuracy. First of all, we fix the size \(L\) of the population. In doing this, we are guided by several considerations: the complexity of the problem, i.e. \(E\left(p_{\gamma}\right)\), the size of the data and computational limits. We have experimented and we recommend to fix \(L\geq 3\). Even though some of the simulated examples had \(p_{\gamma}\simeq 20\) (Section 4.2), we found that \(L=5\) was sufficient to obtain good results. In our real data examples (Section 4.1), we used \(L=4\) guided by some prior knowledge on \(E\left(p_{\gamma}\right)\). Secondly, we fix at an initial stage, a temperature ladder according to a geometric scale such that \(t_{l+1}/t_{l}=b\), \(b>1\), \(l=1,\ldots,L\) with \(b\) relatively large, for instance \(b=4\). To subsequently tune the temperature ladder, we then adopt a strategy based on monitoring only the acceptance rate of the delayed rejection exchange operator towards a target of \(0.5\). Details of the implementation are left in Appendix A.1 ### Adaptive Metropolis-within-Gibbs for \(\tau\) Various strategies can be used to avoid having to sample from the posterior distribution of the variable selection coefficient \(\tau\). The easiest way is to integrate it out through a Laplace approximation (Tierney and Kadane, 1986) or using a numerical integration such as quadrature on an infinite interval. We do not pursue these strategies and the reasons can be summarised as follows. Integrating out \(\tau\) in the population implicitly assumes that every chain has its own value of the variable selection coefficient \(\tau_{l}\) (and of the latent binary vector \(\gamma_{l}\)). In this set-up, two unpleasant situations can arise: firstly, if a Laplace approximation is applied, _equilibrium_ in the product space is difficult to reach because the posterior distribution of \(\gamma_{l}\) depends, through the marginal likelihood obtained using the Laplace approximation, on the _chain specific value_ of the posterior mode for \(\tau_{l}\), \(\hat{\tau}_{\gamma_{l}}\) (details in Appendix A.2). Since the strength of \(X_{\gamma_{l}}\) to predict the response is weakened for chains attached to high temperatures, it turns out that for these chains, \(\hat{\tau}_{\gamma_{l}}\) is likely to be close to zero. When the variable selection coefficient is very small, the marginal likelihood dependence on \(X_{\gamma_{l}}\) decreases even further, see for instance (7), and chains attached to high temperatures will experience a very unstable behaviour, making the convergence in the product space hard to reach. In addition, if an automatic tuning of temperature ladder is applied, chains will increasingly be placed at a closer distance in the temperature ladder to balance the low acceptance rate of the global moves, negating the purpose of EMC. In this paper the convergence is reached instead in the product space \(\prod\nolimits_{l=1}^{L}\left[p\left(\gamma_{l}\left|y,\tau\right.\right) \right]^{1/t_{l}}p\left(\tau\right)\), i.e. the whole population is conditioned on a value of \(\tau\)_common to all chains_. This strategy will alleviate the problems highlighted before allowing for faster convergence and better mixing among the chains. The procedure just described comes with an extra cost, i.e. sampling the value of \(\tau\). However, this step is inexpensive in relation to the cost required to sample \(\gamma_{l}\), \(l=1,\ldots,L\). There are several strategies that can be used to sample \(\tau\) from (11). We found useful to apply the idea of adaptive Metropolis-within-Gibbs described in Roberts and Rosenthal (2008). Conditions for the asymptotic convergence and ergodicity are guaranteed as we enforce the _diminishing adaptive condition_, i.e. the transition kernel stabilises as the number of sweeps goes to infinity and the _bounded convergence condition_, i.e. the convergence time of the kernel is bounded in probability. In our set-up using an adaptive proposal to sample \(\tau\) has several benefits; amongst others it avoids the known problems faced by the Gibbs sampler when the prior is proper, but relatively flat (Natarajan and McCulloch, 1998) as can happen for Z-S priors when \(n\) is large or for the independent case considered by Bae and Mallick (2004). Moreover, given an upper limit on the number of sweeps, the adaptation guarantees a better exploration of the tails of \(p\left(\tau\left|y\right.\right)\) than with a fixed proposal. For details of the implementation and discussion of conditions for convergence, see Appendix A.2. ### ESS algorithm In the following, we refer to our proposed algorithm, Evolutionary Stochastic Search as ESS. If \(g\)-priors are chosen the algorithm is denoted as ESS\(g\), while we use ESS\(i\) if independent priors are selected (the same notation is used when \(\tau\) is fixed or given a prior distribution). Without loss of generality, we assume that the response vector and the design matrix have both been centred and, in the case of independent priors, that the design matrix is also rescaled. Based on the two full conditionals (10) and (11) and the local and global moves introduced earlier, our ESS algorithm can be summarised as follows. * •Given \(\tau\), sample the population’s states \(\bm{\gamma}\) from the two steps: 1. (i)With probability \(0.5\) perform local move and with probability \(0.5\) apply at random one of the four crossover operators: \(1\)-point, uniform, block and adaptive crossover. If local move is selected, use FSMH sampling scheme independently for each chain (see Appendix A.1). Moreover every \(100\) sweeps apply on the first chain a complete scan by a Gibbs sampler. 2. (ii)Perform the delayed rejection exchange operator or the all-exchange operator with equal probability. During the burn-in, only select the delayed rejection exchange operator. * •When \(\tau\) is not fixed but has a prior \(p\left(\tau\right)\), given the latent binary configuration \(\bm{\gamma}=\left(\gamma_{1},\ldots,\gamma_{L}\right)\), sample \(\tau\) from an adaptive Metropolis-within-Gibbs sampling (Section 3.2). From a computational point of view, we used the same fast form for updating \(S\left(\gamma\right)\) as Brown _et al._ (1998), based on the QR-decomposition. Besides its numerical benefits, QR- decomposition can deal with the case \(p_{\gamma}\geq n\). This avoids having to restrict the search to models with \(p_{\gamma}<n\), and helps mixing during the burn-in phase. ## 4 Performance of ESS ### Real data examples The first real data example is an application of linear regression to investigate genetic regulation. To discover the genetic causes of variation in the expression (i.e. transcription) of genes, gene expression data are treated as a quantitative phenotype while genotype data (SNPs) are used as predictors, a type of analysis known as expression Quantitative Trait Loci (eQTL). Here we focus on the ability of ESS to find a parsimonious set of predictors in an animal data set (Hubner _et al._, 2005), where the number of observations, \(n=29\), is small with respect to the number of covariates \(p=1,421\). This situation, where \(n\ll p\), is quite common in animal experiments since environmental sources of variation are controlled as well as the biological diversity of the sample. For illustration, we report the analysis of one gene expression response, where we apply ESS\(g\) with and without the hyperprior on \(\tau\), see Table 1– eQTL. In the former case, thanks to the adaptive proposal, the Markov chain for \(\tau\) mixes very well reaching an overall acceptance rate which is close to the target value \(0.44\). Convergence issue is not a problem since the trace of the proposal’s standard deviation stabilises quickly and well inside the bounded conditions, see Figure 3. In both cases a good mixing among the \(L=4\) chains is obtained (Figure 1, top panels, ESS\(g\) with \(\tau=29\)). Although in the case depicted in Figure 1 with fixed \(\tau\), the convergence is reached in the product space \(\prod\nolimits_{l=1}^{L}\left[p\left(\gamma_{l}\left|y\right.\right)\right]^{1 /t_{l}}\), by visual inspection we see that each chain _marginally_ reaches its _equilibrium_ with respect to the others; moreover, thanks to the automatic tuning of the temperature placement during the burn-in, the distributions of the chains log posterior probabilities overlap nicely, allowing effective exchange of information between the chains. Table 1–eQTL, confirms that the automatic temperature selection works well (with and without the hyperprior on \(\tau\)) reaching an acceptance rate for the monitored exchange (delayed rejection) operator close to the selected target of \(0.50\). The all-exchange operator shows a higher acceptance rate, while, in contrast to Jasra _et al._ (2007), the overall crossover acceptance rate is reasonable high: in our experience the good performance of the crossover operator is both related to the selection operator (Section 3.1) and the new block crossover which shows an acceptance rate far higher than the others. Finally the computational time on the same desktop computer (see details in Appendix B.3) is rather similar with or without the hyperprior \(\tau\), \(28\) and \(30\) minutes respectively for \(25,000\) sweeps with \(5,000\) as burn-in. The main difference among the two implementations of ESS\(g\) is related to the posterior model size: when \(\tau\) is fixed at \(\tau=29\) (Unit Information Prior, Fernández _et al._, 2001), there is more uncertainty and support for larger models, see Figure 2 (a). In both cases we fix \(E\left(p_{\gamma}\right)=4\) and \(V\left(p_{\gamma}\right)=2\), following prior biological knowledge on the genetic regulation. The posterior mean of the variable selection coefficient is a little smaller than the Unit Information Prior, with ESS\(g\) coupled with the Z-S prior favouring smaller models than when \(\tau\) is set equal to \(29\). The best model visited (and the corresponding \(R_{\gamma}^{2}=1-S(\gamma)/y^{T}y\)) is the same for both version of ESS\(g\), while, when a hyperprior on \(\tau\) is implemented, the “stability index” which indicates how much the algorithm persists on the first chain top \(1,000\) (not unique) visited models ranked by the posterior probability (Appendix B.3), shows a higher stability, see Table 1– eQTL. In this case, having a data-driven level of shrinkage helps the search algorithm to better discriminate among competing models. Our second example is related to the application of model (1) in another genomics example: \(10,000\) SNPs, selected genome-wide from a candidate gene study, are used to predict the variation of Mass Spectography metabolomics data in a small human population, an example of a so-called mQTL experiment. A suitable dimension reduction of the data is performed to divide the spectra in regions or bins and \(\log_{10}\)-transformation is applied in order to normalise the signal. We present the key findings related to a particular metabolite bin, but the same comments can be extended to the analysis of the whole data set, where we regressed every metabolites bin _versus_ the genotype data (\(n=50\) and \(p=10,000\)). In this very challenging case, we still found an efficient mixing of the chains (see Table 1–mQTL). Note that in this case the posterior mean of \(\tau\), \(63.577\), is a little larger than the Unit Information Prior, \(\tau=n\), although the influence of the hyperprior is less important than in the previous real data example, see Figure 2 (b). In both examples, the posterior model size favours clearly polygenic control with significant support for up to four genetic control points (Figure 2) highlighting the advantage of performing multivariate analysis in genomics rather than the traditional univariate analysis. As expected in view of the very large number of predictors, in the mQTL example the computational time is quite large, around \(5\) hours for \(20,000\) sweeps after a burn-in of \(5,000\), but as shown in Table 1 by the “stability index” (\(\approx 0\)), we believe that the number of iterations chosen exceeds what is required in order to visit faithfully the model space. For such large data analysis tasks, parallelisation of the code could provide big gains of computer time and would be ideally suited to our multiple chains approach. [Table 1 about here – Figure 1 about here – Figure 2 about here – Figure 3 about here] We also evaluate the superiority of our ESS algorithm, and in particular the FSMH scheme and the block crossover, with respect to more traditional EMC implementations illustrated for instance in Liang and Wong (2000). Albeit we believe that using a wide portfolio of different moves enables any searching algorithm to better explore complicated model spaces, we reanalysed the first real data example, eQTL analysis, comparing: (i) ESS\(g\) with only FSMH as local move _vs_ ESS with only MC\({}^{3}\) as local move; (ii) ESS\(g\) with only block crossover _vs_ ESS\(g\) with only 1-point, only uniform and only adaptive crossover respectively. To avoid dependency of the results on the initialisation of the algorithm, we replicated the analysis \(25\) times. Moreover, to make the comparison fair, in experiment (i) we run the two versions of ESS\(g\) for a different number of sweeps (\(25,000\) and \(350,000\) with \(5,000\) and \(70,000\) as burn-in respectively), but matching the number of models evaluated. Results are presented in Table 2. We report here the main findings: 1. (i)over the \(25\) runs, ESS\(g\) with FSMH reaches the same top visited model \(68\)% (17/25) while ESS\(g\) with MC\({}^{3}\) the same top model only \(28\)%, with a fixed \(\tau\), and \(88\)% and \(40\)% respectively with Z-S prior. This ability is extended to the top models ranked by the posterior probability, data not shown, providing indirect evidence that the proposed new move helps the algorithm to increase its predictive power. The great superiority when FSMH scheme are implemented can be explained by comparing subplot (a) and (c) in Figure 1: the exchange of information between chains for ESS\(g\) with MC\({}^{3}\) as local move when \(p>n\) (and \(p\gg p_{\gamma}\)) is rather poor, negating the purpose of EMC. ESS\(g\) with MC\({}^{3}\) has more difficulties to reach convergence in the product space and, in contrast to ESS\(g\) with FSMH, the retained chain does not easily escape from local modes. This later point can be seen looking at Figure 1 (d) which magnifies the right hand tail of the kernel density of \(\log p\left(\gamma\left|y\right.\right)\) for the recorded chain, pulling together the \(25\) runs: interestingly ESS\(g\) with FSMH is less “bumpy”, showing a better ability to escape from local modes and to explore more efficiently the right tail. 2. (ii)Regarding the second comparison when \(\tau\) is fixed, ESS\(g\) with only block crossover beats constantly the other crossover operators, with \(80\)% _vs_ about \(60\)%, in terms of best model visited (Table 2) and models with higher posterior probability (data not shown), has higher acceptance rate (Table 3), showing also a great capacity to accumulate posterior mass as illustrated in Figure 4. The specific benefit of the block crossover is less pronounced when a prior on \(\tau\) is specified, but we have already noticed that in this case having a hyperprior on \(\tau\) greatly improves the efficiency of the search. [Table 2 about here – Table 3 about here – Figure 4 about here] ### Simulation study We briefly report on a comprehensive study of the performance of ESS in a variety of simulated examples as well as a comparison with SSS. To make comparison with SSS fair, we use ESS\({i}\), the version of our algorithm which assumes independent priors, \(\Sigma_{\gamma}=\tau I_{p_{\gamma}}\),with \(\tau\) fixed at \(1\). Details of the simulated examples (6 set-ups) and how we conducted the simulation experiment (25 replication of each set-up) are given in Appendix B. The rationale behind the construction of the examples was to benchmark our algorithm against both \(n>p\) and \(p>n\) cases, to use as building blocks intricate correlation structures that had been used in previous comparisons by G&McC (1993, 1997) and N&G (2004), as well as a realistic correlation structure derived from genetic data, and to include elements of model uncertainty in some of the examples by using a range of values of regression coefficients. In our example we observe an effective exchange of information between the chains (reported in Table 4) which shows good overall acceptance rates for the collection of moves that we have implemented. The dimension of the problem does not seem to affect the acceptance rates in Table 4, remarkably since values of \(p\) range from \(60\) to \(1,000\) between the examples. We also studied specifically the performance of the global moves (Table 5) to scrutinise our temperature tuning and confirmed the good performance of ESS\(i\) with good frequencies of swapping (not far from the case where adjacent chains are selected to swap at random with equal probability) and good measures of overlap between chains. All the examples were run in parallel with ESS\({i}\) and SSS 2.0 (Hans _et al._, 2007) for the same number of sweeps (22,000) and matching hyperparameters on the model size. Comparison were made with respect to the marginal probability of inclusion as well as the ability to reach models with high posterior probability and to persist in this region. For a detailed discussion of all comparison, see Appendix B.3. Overall the covariates with non-zero effects have high marginal posterior probability of inclusion for ESS\(i\) in all the examples, see Figure 6. There is good agreement between the two algorithms in general, with additional evidence on some examples (Figure 6 (c) and (d)) that ESS\(i\) is able to explore more fully the model space and in particular to find small effects, leading to a posterior model size that is close to the true one. Measures of goodness of fit and stability, Table 6, are in good agreement between ESS\(i\) and SSS. The comparison highlight that a key feature of SSS, its ability to move quickly towards the right model and to persist on it, is accompanied by a drawback in having difficulty to explore far apart models with competing explanatory power, in contrast to ESS\(i\) (contaminated example set-up). Altogether ESS\(i\) shows a small improvement of \(R_{\gamma}^{2}\), related to its ability to pick up some of the small effects that are missed by SSS. Finally ESS\(i\) shows a remarkable superiority in terms of computational time, especially when the simulated (and estimated) \(p_{\gamma}\) is large. Altogether our comparisons show that we have designed a fully Bayesian MCMC-EMC sampler which is competitive with the effective search provided by SSS\(i\). In the same spirit of the real data example analysis, we also evaluate the superiority of the FSMH scheme with respect to more traditional EMC implementations, i.e when a MC\({}^{3}\) local move is selected. While both versions of the search algorithm visit almost the same top models ranked by the posterior probability, ESS persists more on the top models. [Table 4 about here – Table 5 about here – Table 6 about here Figure 5 about here – Figure 6 about here] ## 5 Discussion The key idea in constructing an effective MCMC sampler for \(\gamma\) and \(\tau\) is to add an extra parameter, the temperature, that weakens the likelihood contribution and enables escaping from local modes. Running parallel chains at different temperature is, on the other hand, expensive and the added computational cost has to be balanced against the gains arising from the various “exchanges” between the chains. This is why we focussed on developing a good strategy for selecting the pairs of chains, using both marginal and joint information between the chains, attempting bold and more conservative exchanges. Combining this with an automatic choice of the temperature ladder during burn-in is one of the key element of our ESS algorithm. Using PT in this way has the potential to be effective in a wide range of situations where the posterior space is multimodal. To tackle the case where \(p\) is large with respect to \(p_{\gamma}\), the second important element in our algorithm is the use of a Metropolised Gibbs sampling-like step performed on a subset of indices in the local updating of the latent binary vector, rather than an MC\({}^{3}\) or RJ-like updating move. The new Fast Scan Metropolis Hastings sampler that we propose to perform these local moves achieves an effective compromise between full Gibbs sampling that is not feasible at every sweep when \(p\) is large and vanilla add/delete moves. Comparison of FSMH _vs_ MC\({}^{3}\) scheme on a real data example and simulation study shows the superiority of our new local move. When a model with a prior on the variable selection coefficient \(\tau\) is preferred, the updating of \(\tau\) itself present no particular difficulties and is computationally inexpensive. Moreover, using an adaptive sampler makes the algorithm self contained without any time consuming tuning of the proposal variance. This latter strategy works perfectly well both in the \(g\)-prior and independent prior case as illustrated in Sections 4.1 and 4.2. Our current implementation does not make use of the output of the heated chains for posterior inference. Whether gains in variance reduction could be achieved in the spirit of Gramacy _et al._ (2007) is an area for further exploration, which is beyond the scope of the present work. Our approach has been applied so far to linear regression with univariate response \(y\). An interesting generalisation is that of a multidimensional \(n\times q\) response \(Y\) and the identification of regressors that jointly predict the \(Y\) (Brown _et al._, 1998). Much of our set-up and algorithm carries through without difficulties and we have already implemented our algorithm in this framework in a challenging case study in genomics with multidimensional outcomes. ## Acknowledgements The authors are thankful to Norbert Hubner and Timothy Aitman for providing the data of the eQTL example, Gareth Roberts and Jeffrey Rosenthal for helpful discussions about adaptation and Michail Papathomas for his detailed comments. Sylvia Richardson acknowledges support from the MRC grant GO.600609. ## Appendix A Technical details of EMC implementation In this Section we will describe some technical details omitted from the paper and related to the sampling schemes we used for the population of binary latent vectors \(\bm{\gamma}\) and the selection coefficient \(\tau\). ### EMC sampler for \(\bm{\gamma}\) #### Local move: FSMH scheme Let \(\gamma_{l,j}\), \(l=1,\ldots,L\) and \(j=1,\ldots,p\) to denote the \(j\)th latent binary indicator in the \(l\)th chain. As in Kohn _et al._ (2001), let \(\gamma_{l,j}^{\left(1\right)}=\left(\gamma_{l,1},\ldots,\gamma_{l,j-1},\gamma_ {l,j}=1,\gamma_{l,j+1},\ldots,\gamma_{l,p}\right)^{T}\) and \(\gamma_{l,j}^{\left(0\right)}=\left(\gamma_{l,1},\ldots,\gamma_{l,j-1},\gamma_ {l,j}=0,\gamma_{l,j+1},\ldots,\gamma_{l,p}\right)^{T}\). Furthermore let \(L_{l,j}^{\left(1\right)}\propto p\left(y\left|\gamma_{l,j}^{\left(1\right)}, \tau\right.\right)\) and \(L_{l,j}^{\left(0\right)}\propto p\left(y\left|\gamma_{l,j}^{\left(0\right)}, \tau\right.\right)\) and finally \(\theta_{l,j}^{\left(1\right)}=p\left(\gamma_{l,j}=1\left|\gamma_{l,j^{-}} \right.\right)\) and \(\theta_{l,j}^{\left(0\right)}=1-\theta_{l,j}^{\left(1\right)}\). From (6) it is easy to prove that \[\theta_{l,j}^{\left(1\right)}=p\left(\gamma_{l,j}=1\left|\gamma_{l,j^{-}} \right.\right)=\frac{p_{\gamma_{l}}+a_{\omega}-1}{p+a_{\omega}+b_{\omega}-1},\] (A.1) where \(p_{\gamma_{l}}\) is the current model size for the \(l\)th chain. Using the above equation, for \(\gamma_{l,j}=1\) the normalised version of (12) can be written as \[\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}=\frac{\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left.L_{l ,j}^{\left(1\right)}\right.^{1/t_{l}}}{S\left(1/t_{l}\right)},\] (A.2) where \(S\left(1/t_{l}\right)=\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}} \left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}+\left.\theta_{l,j}^{\left(0 \right)}\right.^{1/t_{l}}\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\) with \(\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}\) defined similarly. Hence if \(\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\) is very small, then \(\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}\) is small as well. Therefore for the Gibbs sampler with a beta-binomial prior on the model space, the posterior probability of \(\gamma_{l,j}=1\) depends crucially on \(\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\). In the following we derive a Fast Scan Metropolis-Hastings scheme specialised for Evolutionary Monte Carlo or parallel tempering. We define \(Q\left(1\to 0\right)=Q\left(\gamma_{l,j}^{\left(1\right)}\to \gamma_{l,j}^{\left(0\right)}\right)\) as the proposal probability to go from \(1\) to \(0\) and \(Q\left(0\to 1\right)\) the proposal probability to go from \(0\) to \(1\) for the \(j\)th variable and \(l\)th chain. Moreover using the notation introduced before, the Metropolis-within-Gibbs version of (12) to go from \(0\) to \(1\) in the EMC local move is \[\alpha_{l}^{\text{MwG}}\left(0\to 1\right)=\min\left\{1,\frac{\left. \theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left.L_{l,j}^{\left(1\right)} \right.^{1/t_{l}}}{\left.\theta_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left.L _{l,j}^{\left(0\right)}\right.^{1/t_{l}}}\frac{Q\left(1\to 0\right)}{Q \left(0\to 1\right)}\right\}\] (A.3) with a similar expression for \(\alpha_{l}^{\text{MwG}}\left(1\to 0\right)\). The proof of the Propositions are omitted since they are easy to check. We first introduce the following Proposition which is useful for the calculation of the acceptance probability in the FSMH scheme. **Proposition 1**: The following three conditions are equivalent: a) \(\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left.\left/L_{l,j}^{\left(1 \right)}\right.^{1/t_{l}}\geq 1\right.\); b) \(\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left/\tilde{S}\left(1/t_{l} \right)\geq 1\right.\); c)\(\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left/\tilde{S}\left(1/t_{l} \right)<1\right.\), where \(\tilde{S}\left(1/t_{l}\right)=S\left(1/t_{l}\right)\left/\left(\left.\theta_{l ,j}^{\left(1\right)}\right.^{1/t_{l}}+\left.\theta_{l,j}^{\left(0\right)} \right.^{1/t_{l}}\right)\right.\) is the convex combination of the marginal likelihood \(\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\) and \(\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\) with weights \(\tilde{\theta}_{l,j}^{\left(1\right)}\left(1/t_{l}\right)=\left.\theta_{l,j}^{ \left(1\right)}\right.^{1/t_{l}}\left/\left(\left.\theta_{l,j}^{\left(1\right) }\right.^{1/t_{l}}+\left.\theta_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\right)\right.\) and \(\tilde{\theta}_{l,j}^{\left(0\right)}\left(1/t_{l}\right)=1-\tilde{\theta}_{l, j}^{\left(1\right)}\left(1/t_{l}\right)\). \({}_{\blacksquare}\) The FSMH scheme can be seen as a random scan Metropolis-within-Gibbs algorithm where the number of evaluations is linked to the prior/current model size and the temperature attached to the chain. The computation requirement for the additional acceptance/rejection step is very modest since the normalised tempered version of (A.1) is used. **Proposition 2**: Let \(l=1,\ldots,L\), \(j=1,\ldots,p\) (or any permutation of them), \(Q^{\text{FSMH}}\left(0\to 1\right)=\tilde{\theta}_{l,j}^{\left(1\right )}\left(1/t_{l}\right)\) and \(Q^{\text{FSMH}}\left(1\to 0\right)=\tilde{\theta}_{l,j}^{\left(0\right )}\left(1/t_{l}\right)\) with \(\tilde{\theta}_{l,j}^{\left(0\right)}\left(1/t_{l}\right)=1-\tilde{\theta}_{l, j}^{\left(1\right)}\left(1/t_{l}\right)\). The acceptance probabilities are \[\alpha_{l}^{\text{FSMH}}\left(0\to 1\right)=\left\{\begin{tabular}[]{ ll}$1$&$\text{if }\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left/\left.L _{l,j}^{\left(0\right)}\right.^{1/t_{l}}\right.\geq 1$\\ $\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(0 \right)}\right.^{1/t_{l}}\right.$&$\text{if }\left.L_{l,j}^{\left(1\right)} \right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\right.< 1$\end{tabular}\right.\] (A.4) \[\alpha_{l}^{\text{FSMH}}\left(1\to 0\right)=\left\{\begin{tabular}[]{ ll}$1$&$\text{if }\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left/\left.L _{l,j}^{\left(1\right)}\right.^{1/t_{l}}\right.\geq 1$\\ $\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(1 \right)}\right.^{1/t_{l}}\right.$&$\text{if }\left.L_{l,j}^{\left(0\right)} \right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}<1\right .$\end{tabular}\right.\] (A.5) \({}_{\blacksquare}\) The above sampling scheme works as follows. Given the \(l\)th chain, if \(\gamma_{lj}=0\) (and similarly for \(\gamma_{lj}=1\)), it proposes the new value from a Bernoulli distribution with probability \(\tilde{\theta}_{l,j}^{\left(1\right)}\left(1/t_{l}\right)\): if the proposed value is different from the current one, it evaluates (A.4) (and similarly A.5)otherwise it selects a new covariate. Finally it can be proved that the Gibbs sampler is more efficient than the FSMH scheme, i.e. for a fixed number of iterations, Gibbs sampling MCMC standard error is lower than for FSMH sampler. However the Gibbs sampler is computationally more expensive so that, if \(p\) is very large, as described in Kohn _et al._ (2001), FSMH scheme becomes more efficient per floating point operation. #### Global move: exchange operator The exchange operator can be seen as an extreme case of crossover operator, where the first proposed chain receives the whole second chain state \(\gamma_{l}^{\prime}=\gamma_{r}\), and the second proposed chain receives the whole first state chain \(\gamma_{r}^{\prime}=\gamma_{l}\), respectively. In order to achieve a good acceptance rate, the exchange operator is usually applied on adjacent chains in the temperature ladder, which limits its capacity for mixing. To obtain better mixing, we implemented two different approaches: the first one is based on Jasra _et al._ (2007) and the related idea of delayed rejection (Green and Mira, 2001); the second one on Gibbs distribution over all possible chains pairs (Calvo, 2005). 1. 1.The delayed rejection exchange operator tries first to swap the state of the chains that are usually far apart in the temperature ladder, but, once the proposed move has been rejected, it performs a more traditional (uniform) adjacent pair selection, increasing the overall mixing between chains on one hand without drastically reducing the acceptance rate on the other. However its flexibility comes at some extra computational costs and in particular the additional evaluation of the pseudo move necessary to maintain detailed balance (Green and Mira, 2001). Details are reported below. Suppose two chains are selected at random, \(l\) and \(r\) with \(l\neq r\), in order to swap their binary latent vector. Then, given that \(\gamma_{l}^{\prime}=\gamma_{r}\), \(\gamma_{r}^{\prime}=\gamma_{l}\) and \(Q_{t}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\right)=Q_{t}\left(\bm{ \gamma}^{\prime}\rightarrow\bm{\gamma}\right)\), (13) reduces to \[\alpha_{1}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\right)=\min\left\{1 ,\frac{\exp\left\{f\left(\gamma_{r}\left|\tau\right.\right)/t_{l}+f\left( \gamma_{l}\left|\tau\right.\right)/t_{r}\right\}}{\exp\left\{f\left(\gamma_{l} \left|\tau\right.\right)/t_{l}+f\left(\gamma_{r}\left|\tau\right.\right)/t_{r} \right\}}\right\}.\] Since the two chains are selected at random, the above acceptance probability decreases exponentially with the difference \(\left|1/t_{l}-1/t_{r}\right|\) and therefore most of the proposed moves are rejected. If rejected, a delayed rejection-type move is applied between two random adjacent chains, with \(l\) the first one and \(s\), \(\left|l-s\right|=1\), the second one, giving rise to the new acceptance probability \[\alpha_{2}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime\prime}\right)=\min \left\{1,\frac{\exp\left\{f\left(\gamma_{s}\left|\tau\right.\right)/t_{l}+f \left(\gamma_{l}\left|\tau\right.\right)/t_{s}\right\}}{\exp\left\{f\left( \gamma_{l}\left|\tau\right.\right)/t_{l}+f\left(\gamma_{s}\left|\tau\right. \right)/t_{s}\right\}}\frac{1-\alpha_{1}\left(\bm{\gamma}^{\prime\prime} \rightarrow\bm{\gamma}^{\ast}\right)}{1-\alpha_{1}\left(\bm{\gamma}\to \bm{\gamma}^{\prime}\right)}\right\},\] where the pseudo move \(\bm{\gamma}^{\ast}\) is necessary in order to maintain the detailed balance condition (Green and Mira, 2001). 2. 2.Alternatively, we attempt a bolder “all-exchange” operator. Swapping the state of two chains that are far apart in the temperature ladder speeds up the convergence of the simulation since it replaces several adjacent swaps with a single move. However, this move can be seen as a rare event whose acceptance probability is low and unknown. Since the full set of possible exchange moves is finite and discrete, it is easy and computationally inexpensive to calculate all the \(L\left(L-1\right)/2\) exchange acceptance rates between all chains pairs, inclusive the rare ones, \(\tilde{p}_{l,r}=\exp\left\{\left(f\left(\gamma_{r}\left|\tau\right.\right)-f \left(\gamma_{l}\left|\tau\right.\right)\right)\left(1/t_{l}-1/t_{r}\right)\right\}\). To maintain detailed balance condition, the possibility not to perform any exchange (rejection) must be added with unnormalised probability one. Finally the chains whose states are swopped are selected at random with probability equal to \[p_{h}=\frac{\tilde{p}_{h}}{\sum_{h=1}^{1+L\left(L-1\right)/2}\tilde{p}_{h}},\] (A.6) where in (A.6) each pair \(\left(l,r<l\right)\) is denoted by a single number \(h\), \(\tilde{p}_{h}=\tilde{p}_{l,r}\), including the rejection move, \(h=1\). #### Temperature placement First we select the number \(L\) of chains close to the complexity of the problem, i.e. \(E\left(p_{\gamma}\right)\), although the size of the data and computational limits need to be taken into account. Secondly, we fix a first stage temperature ladder according to a geometric scale such that \(t_{l+1}/t_{l}=b\), \(b>1\), \(l=1,\ldots,L\) with \(b\) relatively large, for instance \(b=4\). Finally, we adopt a strategy similar to the one described in Roberts and Rosenthal (2008), but _restricted to the burn-in stage_, monitoring only the acceptance rate of the delayed rejection exchange operator. After the \(k\)th “batch” of EMC sweeps, to be chosen but usually set equal to \(100\), we update \(b_{k}\), the value of the constant \(b\) up to the \(k\)th batch, by adding or subtracting an amount \(\delta_{b}\) such that the acceptance rate of the delayed rejection exchange operator is as close as possible to \(0.50\) (Liu, 2001; Jasra _et al._, 2007), \(b_{k+1}=2^{\log_{2}b_{k}\pm\delta_{b}}\). Specifically the value of \(\delta_{b}\) is chosen such that at the end of the burn-in period the value of \(b\) can be 1. To be precise, we fix the value of \(\delta_{b}\) as \(\log_{2}\left(b_{1}\right)/\tilde{K}\), where \(b_{1}\) is the first value assigned to the geometric ratio and \(\tilde{K}\) is the total number of batches in the burn-in period. ### Adaptive Metropolis-within-Gibbs for \(\tau\) #### Laplace approximation for the conditional marginal likelihood Under model (1) and prior specification for \(\alpha\), (2) and (3), we provide the Laplace approximation of \(p\left(y\left|\gamma,\tau\right.\right)\) for the \(g\)-prior case, while the approximation for the independent case can be derived following the same line of reasoning. For easy of notation we drop the chain subscript index and we assume that the observed responses \(y\) have been centred with mean \(0\), i.e. \(\left(y-\bar{y}_{n}\right)\equiv y\). In the following we will distinguish the cases in which the posterior mode \(\hat{\tau}_{\gamma}\) is a solution of a cubic or quadratic equation. Conditions on the existence of the solutions are provided as well as those that guarantee the positive semidefiniteness of the variance approximation. Recall that \[p\left(y\left|\gamma\right.\right) = \int\exp\left\{\log\left(p\left(y\left|\gamma,\tau\right.\right)p \left(\tau\right)\right)\right\}d\tau\] \[\approx \sqrt{2\pi}\sigma_{\hat{\lambda}}\left(\log p\left(y\left|\gamma, \hat{\lambda}\right.\right)+\log p\left(\hat{\lambda}\right)+\log J\left(\hat{ \lambda}\right)\right),\] where \(\hat{\lambda}\) is the posterior mode after the transformation \(\lambda=\log\left(\tau\right)\), which is necessary to avoid problems on the boundary, \(\sigma_{\hat{\lambda}}\) is the approximate squared root of the variance calculated in \(\hat{\lambda}\) and \(J\left(\cdot\right)\) is the Jacobian of the transformation. Details about Laplace approximation can be found in Tierney and Kadane (1986). Similar derivations when \(p\left(\sigma^{2}\right)\propto\sigma^{-2}\) are presented in Liang _et al._ (2008). Finally throughout the presentation we will assume that \(n>p_{\gamma}\) and that \(a_{g}\) and \(b_{g}\) are fixed small as in Kohn _et al._ (2001). Cubic equation for Zellner-Siow priors If \(p\left(\tau\right)=InvGa\left(a_{\tau},b_{\tau}\right)\) the posterior \(\hat{\lambda}\) mode is the only positive root of the integrand function \[I_{\lambda}=\left(1+e^{\lambda}\right)^{\left(2a_{\sigma}+n-1-p_{\gamma}\right )/2}\left\{2b_{\sigma}\left(1+e^{\lambda}\right)+y^{T}y\left[1+e^{\lambda} \left(1-R_{\gamma}^{2}\right)\right]\right\}^{-\left(2a_{\sigma}+n-1\right)/2} \frac{e^{-b_{\tau}/e^{\lambda}}}{\left(e^{\lambda}\right)^{a_{\tau}+1}}e^{ \lambda},\] where the last factor in the above equation \(e^{\lambda}=\left|de^{\lambda}/d\lambda\right|\) is the Jacobian of the transformation. After the calculus of the first derivative of the log transformation and some algebra manipulations, it can be shown that \(e^{\hat{\lambda}}\) is the solution of the cubic equation \[e^{3\lambda}+\frac{c_{1}c_{3}-c_{2}c_{4}-\left(c_{3}+c_{4}\right)a_{\tau}+c_{4 }b_{\tau}}{\left(c_{1}-c_{2}-a_{\tau}\right)c_{4}}e^{2\lambda}+\frac{-c_{3}a_{ \tau}+\left(c_{3}+c_{4}\right)b_{\tau}}{\left(c_{1}-c_{2}-a_{\tau}\right)c_{4} }e^{\lambda}+\frac{c_{3}b_{\tau}}{\left(c_{1}-c_{2}-a_{\tau}\right)c_{4}}=0\] (A.7) and that \[\sigma_{\hat{\lambda}}^{2} = \left.-\frac{1}{\left(\log p\left(y\left|\gamma,\lambda\right. \right)+\log p\left(\lambda\right)\right)^{\prime\prime}}\right|_{\lambda=\hat {\lambda}}\] (A.8) \[= \left[-c_{1}\frac{e^{\lambda}}{\left(1+e^{\lambda}\right)^{2}}+c_ {2}\frac{c_{3}c_{4}e^{\lambda}}{\left(c_{3}+c_{4}e^{\lambda}\right)^{2}}+\frac {b_{\tau}}{e^{\lambda}}\right]_{\lambda=\hat{\lambda}}^{-1},\] where \(c_{1}=\left(2a_{\sigma}+n-1-p_{\gamma}\right)/2\), \(c_{2}=\left(2a_{\sigma}+n-1\right)/2\), \(c_{3}=2b_{\sigma}+y^{T}y\) and \(c_{4}=2b_{\sigma}+y^{T}y\left(1-R_{\gamma}^{2}\right)\). Following Liang _et al._ (2008), since \(\lim_{\lambda\rightarrow-\infty}\partial I_{\lambda}/\partial\lambda>0\), because \(c_{3}b_{\tau}>0\), and \(\lim_{\lambda\rightarrow\infty}\partial I_{\lambda}/\partial\lambda<0\), because \(\left(c_{1}-c_{2}-a_{\tau}\right)c_{4}<0\), at least one real positive solution exists. Moreover since \(-\left(c_{3}b_{\tau}\right)/\left(c_{1}-c_{2}-a_{\tau}\right)c_{4}>0\), the remaining two real solutions should have the same sign (Abramowitz and Stegun, 1970). A necessary condition for the existence of just one real positive solution is that the summation of all the pairs-products of the coefficients is negative \[\frac{-c_{3}a_{\tau}+\left(c_{3}+c_{4}\right)b_{\tau}}{\left(c_{1}-c_{2}-a_{ \tau}\right)c_{4}}<0\] and this happens if \(b_{\tau}/a_{\tau}>c_{3}/\left(c_{3}+c_{4}\right)\). When \(R_{\gamma}^{2}\to 0\) and thus \(c_{3}=c_{4}\), the above condition corresponds to \(b_{\tau}>a_{\tau}/2\) and when \(R_{\gamma}^{2}\to 1\), as \(c_{3}/\left(c_{3}+c_{4}\right)\approx 1\) especially when \(y^{T}y\) is large, which might be expected when \(n\) becomes large, the condition is equivalent to \(b_{\tau}>a_{\tau}\). Therefore it turns out that a sufficient condition for the existence of just one real positive solution in (A.1) is \(b_{\tau}>a_{\tau}\). The positive semidefiniteness of the approximate variance can be proved as follows. First of all it is worth noticing that all the terms in (A.8) are of the same order \(O_{p}\left(e^{-\lambda}\right)\). Then, when \(R_{\gamma}^{2}\to 0\), the positive semidefiniteness is always guaranteed, while when \(R_{\gamma}^{2}\to 1\), provided that \(y^{T}y\) is large, the middle term in (A.8) tends to zero and the condition is fulfilled if \(b_{\tau}>c_{1}\). Quadratic equation for Liang _et al._ (2008) prior If \(p\left(\tau\right)\propto\left(1+\tau\right)^{-c_{\tau}}\), with \(c_{\tau}>0\), \(e^{\hat{\lambda}}\) is only the positive root of the integrand function \[I_{\lambda}=\left(1+e^{\lambda}\right)^{\left(2a_{\sigma}+n-1-p_{\gamma}-c_{ \tau}\right)/2}\left\{2b_{\sigma}\left(1+e^{\lambda}\right)+y^{T}y\left[1+e^{ \lambda}\left(1-R_{\gamma}^{2}\right)\right]\right\}^{-\left(2a_{\sigma}+n-1 \right)/2}e^{\lambda}\] or, after the first derivative of the log transformation, the solution of the quadratic equation \[\left(c_{1}^{\ast}-c_{2}+1\right)c_{4}e^{2\lambda}+\left(c_{1}^{\ast}c_{3}-c_{ 2}c_{4}+c_{3}+c_{4}\right)e^{\lambda}+c_{3}=0\] (A.9) with \(c_{1}^{\ast}=\left[2a_{\sigma}+n-1-\left(p_{\gamma}+2c_{\tau}\right)\right]/2\) and \(c_{2}\), \(c_{3}\) and \(c_{4}\) defined as above. The discriminant of the quadratic equation is \(\Delta=\left(c_{1}^{\ast}c_{3}-c_{2}c_{4}c_{3}+c_{3}+c_{4}\right)^{2}-4\left(c _{1}^{\ast}-c_{2}+1\right)c_{4}c_{3}\) which is always greater than zero and therefore two real roots exist. Since one of them is positive in order to prove that (A.9) admits just one positive solution, it is necessary to show that \[\frac{-\left(c_{1}^{\ast}c_{3}-c_{2}c_{4}+c_{3}+c_{4}\right)-\Delta^{1/2}}{2 \left(c_{1}^{\ast}-c_{2}+1\right)c_{4}}<0\] which is true provided that \(\left(c_{1}^{\ast}-c_{2}+1\right)c_{4}c_{3}<0\). Moreover the approximate variance can be written as \[\sigma_{\hat{\lambda}}^{2}=\left[-c_{1}^{\ast}\frac{e^{\lambda}}{\left(1+e^{ \lambda}\right)^{2}}+c_{2}\frac{c_{3}c_{4}e^{\lambda}}{\left(c_{3}+c_{4}e^{ \lambda}\right)^{2}}\right]_{\lambda=\hat{\lambda}}^{-1}\] (A.10) which is positive semidefinite when \(R_{\gamma}^{2}\to 0\) if \(c_{2}>c_{1}^{\ast}\), which is always verified, while, if \(R_{\gamma}^{2}\to 1\) and \(y^{T}y\) is large, equation (A.10) is not positive unless \(p_{\gamma}+2c_{\tau}>2a_{\sigma}+n-1\). The explicit solution of the posterior mode is also available \[\hat{\tau}_{\gamma} = \max\left\{\frac{\left(c_{4}-c_{3}\right)/\left(c_{1}^{\ast}-c_{2 }\right)}{c_{4}/c_{1}^{\ast}}-1,0\right\}\] (A.11) \[= \max\left\{\frac{R_{\gamma}^{2}/\left(p_{\gamma}+2c_{\tau}\right) }{\left[2b_{\sigma}/\left(y^{T}y\right)+\left(1-R_{\gamma}^{2}\right)\right]/ \left[2a_{\sigma}+n-1-\left(p_{\gamma}+2c_{\tau}\right)\right]}-1,0\right\}\] which corresponds to MLE if \(c_{\tau}=0\). #### Diminishing adaptive and bounded conditions Since \(\tau\) is defined on the real positive axis we propose the new value of \(\tau\) on the logarithm scale. In particular we use as proposal the normal distribution centred at the current value of \(\log\left(\tau\right)\) in the \(g\)-prior and independent prior case. The variance of the proposal distribution is controlled as illustrated in Roberts and Rosenthal (2008): every \(100\) EMC sweeps, the same value of sweeps used in the temperature placement, we monitor the acceptance rate of the Metropolis-within-Gibbs algorithm: if it is lower (higher) than the optimal acceptance rate, i.e. 0.44, a constant \(\delta_{\tau}(k)\) is added (subtracted) to \(ls_{k}\), the log standard deviation of the proposal distribution in the \(k\)th batch of EMC sweeps. The value of the constant to be added or subtracted is rather arbitrary, but we found useful to fix it as \(\left|ls_{1}-5\right|/\tilde{K}\), where \(\tilde{K}\) is the total number of batches in the burn-in period: during the burn-in the log standard deviation should be able to reach any values at a distance \(\pm 5\) in log scale from the initial value of \(ls_{1}\) usually set equal to zero. The _diminishing adaptive condition_ is obtained imposing \(\delta_{\tau}\left(k\right)=\min\{\left|ls_{1}-5\right|/\tilde{K},k^{-1/2}\}\), where \(k\) is the current number of batches, including the burn-in. To ensure the _bounded convergence condition_ we follow Roberts and Rosenthal (2008), restricting each \(ls_{k}\) to be inside \(\left[M_{1},M_{2}\right]\) and we fix them equal to \(M_{1}=-10\) and \(M_{2}=10\) respectively. In practise these bounds do not create any restriction since the sequence of the standard deviations of the proposal distribution stabilises almost immediately, indicating that the transition kernel converges in a bounded number of batches, see Figure 2. ## Appendix B Performance of ESS: Simulation study In this Section we report in details on the performance of ESS in a variety of simulated examples. Main conclusions are summarised in the Section 4.2. Firstly we analyse the simulated examples with ESS\({i}\) the version of our algorithm which assumes independent priors, \(\Sigma_{\gamma}=\tau I_{p_{\gamma}}\), so as to enable comparisons with SSS which also implements an independent prior. Moreover, in order to make to comparison with SSS fair, in the simulation study only the first step of the algorithm described in Section 3.3 is performed, with \(\tau\) fixed at \(1\). As in SSS, standardisation of the covariates is done before running ESS\({i}\). We run ESS\({i}\) and SSS 2.0 (Hans _et al._, 2007) for the same number of sweeps (22,000) and with matching hyperparameters on the model size. Secondly, to discuss the mixing properties of ESS when a prior \(p\left(\tau\right)\) is defined on \(\tau\), we implement both the \(g\)-prior and independent prior set-up for a particular simulated experiment. To be precise in the former case we will use the Zellner-Siow priors (8), and for the latter we will specify a proper but diffuse exponential distribution as suggested by Bae and Mallick (2004). ### Simulated experiments We apply ESS with independent priors to an extensive and challenging range of simulated examples with \(\tau\) fixed at \(1\): the first three examples (Ex1-Ex3) consider the case \(n>p\) while the remaining three (Ex4-Ex6) have \(p>n\). Moreover in all examples, except the last one, we simulate the design matrix, creating more and more intricated correlation structures between the covariates in order to test the proposed algorithm in different and increasingly more realistic scenarios. In the last example, we use, as design matrix, a genetic region spanning \(500\)-kb from the HapMap project (Altshuler _et al._, 2005). Simulated experiments Ex1-Ex5 share in common the way we build \(X\). In order to create moderate to strong correlation, we found useful referring to two simulated examples in George and McCulloch, G&McC hereafter, (1993) and in G&McC (1997): throughout we call \(X_{1}\) (\(n\times 60\)) and \(X_{2}\)\((n\times 15)\) the design matrix obtained from these two examples. In particular the \(j\)th column of \(X_{1}\), indicated as \(X_{\left(1\right)j}\), is simulated as \(X_{\left(1\right)j}=X_{j}^{\ast}+Z\), where \(X_{1}^{\ast},\ldots,X_{60}^{\ast}\) iid \(\sim N_{n}\left(0,1\right)\) independently form \(Z\sim N_{n}\left(0,1\right)\), inducing a pairwise correlation of \(0.5\). \(X_{2}\) is generated as follows: firstly we simulated \(Z_{1},\ldots,Z_{15}\) iid \(\sim N_{n}\left(0,1\right)\) and we set \(X_{\left(2\right)j}=Z_{i}+2Z_{j}\) for \(j=1,3,5,8,9,10,12,13,14,15\) only. To induce strong multicollinearity, we then set \(X_{\left(2\right)2}=X_{\left(2\right)1}+0.15Z_{2}\), \(X_{\left(2\right)4}=X_{\left(2\right)3}+0.15Z_{4}\), \(X_{\left(2\right)6}=X_{\left(2\right)5}+0.15Z_{6}\), \(X_{\left(2\right)7}=X_{\left(2\right)8}+X_{\left(2\right)9}-X_{\left(2\right)1 0}+0.15Z_{7}\) and \(X_{\left(2\right)11}=X_{\left(2\right)14}+X_{\left(2\right)15}-X_{\left(2 \right)12}-X_{\left(2\right)13}+0.15Z_{11}\). A pairwise correlation of about 0.998 between \(X_{\left(2\right)j}\) and \(X_{\left(2\right)j+1}\) for \(j=1,3,5\) is introduced and similarly strong linear relationship is present within the sets \(\left(X_{\left(2\right)7},X_{\left(2\right)8},X_{\left(2\right)9},X_{\left(2 \right)10}\right)\) and \(\left(X_{\left(2\right)11},X_{\left(2\right)12},X_{\left(2\right)13},X_{\left( 2\right)14},X_{\left(2\right)15}\right)\). Then, as in Nott and Green, N&G hereafter, (2004) Example 2, more complex structures are created by placing side by side combinations of \(X_{1}\) and/or \(X_{2}\), with different sample size. We will vary the number of samples \(n\) in \(X_{1}\) and \(X_{2}\) as we construct our examples. The levels of \(\beta\) are taken from the simulation study of Fernández _et al._ (2001), while the number of true effects, \(p_{\gamma}\), with the exception of Ex3, varies from \(5\) to \(16\). Finally the simulated error variance ranges from \(0.05^{2}\) to \(2.5^{2}\) in order to vary the level of difficulty for the search algorithm. Throughout we only list the non-zero \(\beta_{\gamma}\) and assume that \(\beta_{\gamma^{-}}=0^{T}\). The six examples can be summarised as follows: * **Ex1**:\(X=X_{1}\) is a matrix of dimension \(120\times 60\), where the responses are simulated from (1) using \(\alpha=0\), \(\gamma=\left(21,37,46,53,54\right)^{T}\), \(\beta_{\gamma}=\left(2.5,0.5,-1,1.5,0.5\right)^{T}\), and \(\varepsilon\sim N\left(0,2^{2}I_{120}\right)\). In the following we will not refer to the intercept \(\alpha\) any more since, as described in Section 3.3 in the paper, we consider \(y\) centred and hence there is no difference in the results if the intercept is simulated or not. This is the simplest of our example, although, as reported in G&McC (1993) the average pairwise correlation is about \(0.5\), making it already hard to analyse by standard stepwise methods. * **Ex2**:This example is taken directly from N&G (2004), Example 2, who first introduce the idea of combining simpler “building blocks” to create a new matrix \(X\) : in their example \(X=\left[X_{2}^{\left(1\right)}X_{2}^{\left(2\right)}\right]\) is a \(300\times 30\) matrix, where \(X_{2}^{\left(1\right)}\) and \(X_{2}^{\left(2\right)}\) are of dimension \(300\times 15\) and have each the same structure as \(X_{2}\). Moreover \(\gamma=\left(1,3,5,7,8,11,12,13\right)^{T}\), \(\beta_{\gamma}=\left(1.5,1.5,1.5,1.5,-1.5,1.5,1.5,1.5\right)^{T}\) and \(\varepsilon\sim N\left(0,2.5^{2}I_{300}\right)\). We chose this example for two reasons: firstly, since the correlation structure in \(X_{2}\) is very involved, we test the proposed algorithm under strong and complicated correlations between the covariates; secondly, since \(y\) is not simulated from the second “block”, we are interested to see if the proposed algorithm does _not_ select any variable that belongs to the second group. * **Ex3**:As in G&McC (1993), Example 2, \(X=X_{1}\), is a \(120\times 60\) matrix, \(\beta=\left(\beta_{1},\ldots,\beta{}_{60}\right)^{T}\), \(\left(\beta_{1},\ldots,\beta_{15}\right)=\left(0,\ldots,0\right)\), \(\left(\beta_{16},\ldots,\beta_{30}\right)=\left(1,\ldots,1\right)\), \(\left(\beta_{31},\ldots,\beta_{45}\right)=\left(2,\ldots,2\right)\), \(\left(\beta_{46},\ldots,\beta_{60}\right)=\left(3,\ldots,3\right)\) and \(\varepsilon\sim N\left(0,2^{2}I_{120}\right)\). The motivation behind this example is to test the strength of the proposed algorithm to select a subset of variables which is large with respect to \(p\) while preserving the ability _not_ to choose any of the first \(15\) variables. * **Ex4**:The design matrix \(X\), \(120\times 300\), is constructed as follows: firstly we create a new \(120\times 60\) “building block”, \(X_{3}\), combining \(X_{2}\) and a smaller version of \(X_{1}\), \(X_{1}^{\ast}\), a \(120\times 45\) matrix simulated as \(X_{1}\), such that \(X_{3}=\left[X_{2}X_{1}^{\ast}\right]\) (dimension \(120\times 60\)). Secondly we place side by side five copies of \(X_{3}\), \(X=\left[X_{3}^{\left(1\right)}X_{3}^{\left(2\right)}X_{3}^{\left(3\right)}X_{3 }^{\left(4\right)}X_{3}^{\left(5\right)}\right]\): the new design matrix alternates blocks of covariates of high and complicated correlation, as in G&McC (1997), with regions where the correlation is moderate as in G&McC (1993). We simulate the response selecting \(16\) variables from \(X\), \(\gamma=\left(1,11,30,45,61,71,90,105,121,131,150,165,181,191,210,225\right)^{T}\) such that every pair belongs alternatively to \(X_{2}\) or \(X_{1}\). We simulate \(y\) using \(\beta_{\gamma}=\left(2,-1,1.5,1,0.5,2,-1,1.5,1,0.5,2,-1,-1,1.5,1,0.5\right)^{T}\) with \(\varepsilon\sim N\left(0,2.5^{2}I_{120}\right)\). This example is challenging in view of the correlation structure, the number of covariates \(p>n\) and the different levels of the effects. * **Ex5**:This is the most challenging example that we simulated and it is based on the idea of contaminated models. The matrix \(X\), \(200\times 1000\), is \(X=\left[X_{3}^{\left(1\right)}X_{3}^{\left(2\right)}X_{3}^{\left(3\right)}X_{1 }^{\ast\ast}X_{3}^{\left(4\right)}X_{3}^{\left(5\right)}X_{3}^{\left(6\right)} X_{3}^{\left(7\right)}X_{3}^{\left(8\right)}\right]\), with \(X_{1}^{\ast\ast}\), a \(200\times 520\) larger version of \(X_{1}\). We partitioned the responses such that \(y=[y_{1}y_{2}]^{T}\): \(y_{1}\) is simulated from “model 1” (\(\gamma^{1}=\left(701,730,745,763,790,805,825,850,865,887\right)\) and \(\beta_{\gamma}^{1}=\left(2,-1,1.5,1,0.5,2,-1,1.5,2,-1\right)\)) while \(y_{2}\) is simulated from “model 2” (\(\gamma^{2}=\left(1,38,63,98,125\right)\) and \(\beta_{\gamma}^{2}=\left(2,-1,1.5,1,0.5\right)\)). Finally, fixing \(\varepsilon\sim N\left(0,0.05^{2}I_{200}\right)\) and the sample size in the two models such that \(y_{1}\) and \(y_{2}\) are vectors of dimension \(1\times 160\) and \(1\times 40\) respectively, \(y\) is retained if, given the sampling variability, we find \(R_{\gamma^{1}}^{2}\geq 0.6\) and \(R_{\gamma^{1}}^{2}/8\leq R_{\gamma^{2}}^{2}\leq R_{\gamma^{1}}^{2}/10\): in this way we know that “model 1” accounts for most of the variability of \(y\), but without a negligible effect for “model 2”. In this example, we measure the ability of the proposed algorithm to recognise the most promising model and therefore being robust to contaminations. However since ESS can easily jump between local modes we are also interested to see if “model 2” is selected. * **Ex6**:The last simulated example is based on phased genotype data from HapMap project (Altshuler _et al._, 2005), region ENm014, Yoruba population: the data set originally contained 1,218 SNPs (Single Nucleotide Polymorphism) for 120 chromosomes, but after eliminating redundant variables, the design matrix reduced to \(120\times 775\). While in the previous examples a “block structure” of correlated variables is artificially constructed, in this example blocks of linkage disequilibrium (LD) derive naturally from genetic forces, with a slow decay of the level of pairwise correlation between SNPs. Finally we chose \(\gamma=\left(50,75,140,200,300,400,500,650,700,770\right)^{T}\) such that the effects are visually inside blocks of LD, with their size simulated from \(\beta_{\gamma}\sim N\left(0,3^{2}I_{10}\right)\) with \(\varepsilon\sim N\left(0,0.10^{2}I_{120}\right)\). Since the simulated effects can range roughly between \(\left(-6,6\right)\), this will allow us to test also the ability of ESS\(i\) to select small effects. We conclude this Section by reporting how we conducted the simulation experiment: every example from Ex1 to Ex6 has been replicated \(25\) times and the results presented for example Ex1 to Ex5 are averaged over the \(25\) replicates. For Ex6 the effects size change so average across replicated is only done for the mixing properties. ESS\(i\) with \(\tau\) =1 was applied to each example/sample, recording the visited sequence of \(\gamma_{1}\) for \(20,000\) sweeps after a burn-in of \(2,000\) required for the automatic tuning of the temperature placement, Section 3.1 With the exception of Ex2 and Ex3, where we used an indifferent prior, \(p\left(\gamma\right)=\left(1/2\right)^{p}\), we analysed the remaining examples setting \(E\left(p_{\gamma}\right)=5\) with \(V\left(p_{\gamma}\right)=E\left(p_{\gamma}\right)\left(1-E\left(p_{\gamma} \right)/p\right)\) which corresponds to a binomial prior over \(p_{\gamma}\). In order to establish the sensitivity of the proposed algorithm to the choice of \(E\left(p_{\gamma}\right)\) we also analysed Ex1 fixing \(E\left(p_{\gamma}\right)=10\) and \(20\). Moreover in all the examples we chose \(L=5\) with the starting value of \(\bm{\gamma}\) chosen at random. The remaining two hyperparameters to be fixed, namely \(a_{\sigma}\) and \(b_{\sigma}\), are set equal to \(a_{\sigma}=10^{-6}\) and \(b_{\sigma}=10^{-3}\) as in Kohn _et al._ (2001) which corresponds to a relative uninformative prior. ### Mixing properties of ESS\({i}\) In this Section we report some stylised facts about the performance of the ESS\({i}\) with \(\tau\) fixed at \(1\). Figure 5, top panels, shows for one of the replicates of Ex1, the overall mixing properties of ESS\(i\). As expected, the chains attached to higher temperatures shows more variability. Albeit the convergence is reached in the product space \(\prod\nolimits_{l=1}^{L}\left[p\left(\gamma_{l}\left|y\right.\right)\right]^{1 /t_{l}}\), by visual inspection each chain _marginally_ reaches its _equilibrium_ with respect to the others; moreover, thanks to the automatic tuning of the temperature placement during the burn-in, the distributions of their log posterior probabilities overlap nicely, allowing effective exchange of information between the chains. Figure 5, bottom panels, shows the trace plot of the log posterior and the model size for a replicate of Ex4. We can see that also in the case \(p>n\), the chains mix and overlap well with no gaps between them, the automatic tuning of the temperature ladder being able to improve drastically the performance of the algorithm. This effective exchange of information is demonstrated in Table 4 which shows good overall acceptance rates for the collection of moves that we have implemented. The dimension of the problem does not seem to affect the acceptance rate of the (delayed rejection) exchange operator which stays very stable and close to the target: for instance in Ex4 (\(p=300\)) and Ex6 (\(p=775\)) the mean and standard deviation of the acceptance rate are \(0.517\) (\(0.105\)) and \(0.497\) (\(0.072\)) while in Ex5 (\(p=1,000\)) we have \(0.505\) (\(0.013\)): the higher variability in Ex4 being related to the model size \(p_{\gamma}\). With regards to the crossover operators, again we observe stability across all the examples. Moreover, in contrast to Jasra _et al._ (2007), when \(p>n\), the crossover average acceptance rate across the five chains is quite stable between \(0.147\), Ex4, and \(0.193\), Ex6 (with the lower value in Ex4 here again due to \(p_{\gamma}\)): within our limited experiments, we believe that the good performance of crossover operator is related to the selection operator and the new block crossover, see Section 3.1. Some finer tuning of the temperature ladder could still be performed as there seems to be an indication that fewer global moves are accepted with the higher temperature chain, see Table 5, where swapping probabilities for each chain are indicated. Note that the observed frequency of successful swaps is not far from the case where adjacent chains are selected to swap at random with equal probability. Other measures of overlapping between chains (Liang and Wong, 2000; Iba 2001), based on a suitable index of variation of \(f\left(\gamma\right)=\log p\left(y\left|\gamma\right.\right)+\log p\left( \gamma\right)\) across sweeps, confirm the good performance of ESS\(i\). Again some instability is present in the high temperature chains, see in Table 5 the overlapping index between chains \(3,4\) and \(4,5\) in Example 3 to 6. In Ex1, we also investigate the influence of different values of the prior mean of the model size. We found that the average (standard deviation in brackets) acceptance rate across replicates for the delayed rejection exchange operator ranges from \(0.493\) (\(0.043\)) to 0.500 (0.040) for different values of the prior mean on the model size, while the acceptance rate for the crossover operator ranges from \(0.249\) (\(0.021\)) to \(0.271\) (\(0.036\)). This strong stability is not surprising because the automatic tuning modifies the temperature ladder in order to compensate for \(E\left(p_{\gamma}\right)\). Finally we notice that the acceptance rates for the local move, when \(n>p\), increases with higher values of the prior mean model size, showing that locally the algorithm moves more freely with \(E\left(p_{\gamma}\right)=20\) than with \(E\left(p_{\gamma}\right)=5\). ### Performance of ESS\(i\) and comparison with SSS #### Performance of ESS\(i\) We conclude this Section by discussing in details the overall performance of ESS\(i\) with respect to the selection of the true simulated effects. As a first measure of performance, we report for all the simulated examples the marginal posterior probability of inclusion as described in G&McC (1997) and Hans _et al._ (2007). In the following, for ease of notation, we drop the chain subscript index and we exclusively refer to the first chain. To be precise, we evaluate the marginal posterior probability of inclusion as: \[p\left(\gamma_{j}=1\left|y\right.\right)\simeq C^{-1}\sum_{t=1,\ldots,T}1_{ \left(\gamma_{j}^{\left(t\right)}=1\right)}\left(\gamma\right)p\left(y\left| \gamma^{\left(t\right)}\right.\right)p\left(\gamma^{\left(t\right)}\right)\] (A.12) with \(C=\sum_{t=1,\ldots,T}p\left(y\left|\gamma^{\left(t\right)}\right.\right)p\left (\gamma^{\left(t\right)}\right)\) and \(T\) the number of sweeps after the burn-in. The posterior model size is similarly defined, \(p\left(p_{\gamma}\left|y\right.\right)\simeq C^{-1}\sum_{t=1,\ldots,T}1_{\left (\left|\gamma^{\left(t\right)}\right|=p_{\gamma}\right)}\left(\gamma\right)p \left(y\left|\gamma^{\left(t\right)}\right.\right)p\left(\gamma^{\left(t\right )}\right)\), with \(C\) as before. Besides plotting the marginal posterior inclusion probability (A.12) averaged across sweeps and replicates for our simulated examples, we will also compute the interquartile range of (A.12) across replicates as a measure of variability. In order to thoroughly compare the proposed ESS algorithm to SSS (Hans _et al._, 2007), we present also some other measures of performance based on \(p\left(\gamma\left|y\right.\right)\) and \(R_{\gamma}^{2}\) : first we rank \(p\left(\gamma\left|y\right.\right)\) in decreasing order and record the indicator \(\gamma\) that corresponds to the maximum and \(1,000\) largest \(p\left(\gamma\left|y\right.\right)\) (after burn-in). Given the above set of latent binary vectors, we then compute the corresponding \(R_{\gamma}^{2}\) leading to “\(R_{\gamma}^{2}\): \(\max p\left(\gamma\left|y\right.\right)\)” as well as the mean \(R_{\gamma}^{2}\) over the \(1,000\) largest \(p\left(\gamma\left|y\right.\right)\), “\(\overline{R_{\gamma}^{2}}\): \(1,000\) largest \(p\left(\gamma\left|y\right.\right)\)”, both quantities averaged across replicates. Moreover the actual ability of the algorithm to reach regions of high posterior probability and persist on them is monitored: given the sequence of the \(1,000\) best \(\gamma\)s (based on \(p\left(\gamma\left|y\right.\right)\)), the standard deviation of the corresponding \(R_{\gamma}^{2}\)s shows how stable is the searching strategy at least for the top ranked (not unique) posterior probabilities: averaging over the replicates, it provides an heuristic measures of “stability” of the algorithm. Finally we report the average computational time (in minutes) across replicates of ESS\(i\) written in Matlab code and run on a 2MHz CPU with 1.5 Gb RAM desktop computer and of SSS version 2.0 on the same computer. #### Comparison with SSS Figure 6 presents the marginal posterior probability of inclusion for ESS\(i\) with \(\tau=1\) averaged across replicates and, as a measure of variability, the interquartile range, blue left triangles and vertical blue solid line respectively. In general the covariates with non-zero effects have high marginal posterior probability of inclusion in all the examples: for example in Ex3, Figure 6 (a), the proposed ESS\(i\) algorithm, blue left triangle, is able to perfectly select the last \(45\) covariates, while the first \(15\), which do not contribute to \(y\), receive small marginal posterior probability. It is interesting to note that this group of covariates, \(\left(\beta_{1},\ldots,\beta_{15}\right)=\left(0,\ldots,0\right)\), although correctly recognised having no influence on \(y\), show some variability across replicates, vertical blue solid line: however, this is not surprising since independent priors are less suitable in situations where all the covariates are mildly-strongly correlated as in this simulated example. On the other hand the second set of covariates with small effects, \(\left(\beta_{16},\ldots,\beta_{30}\right)=\left(1,\ldots,1\right)\), are univocally detected. The ability of ESS\(i\) to select variables with small effects is also evident in Ex6, Figure 6 (d), where the two smallest coefficients, \(\beta_{2}=0.112\) and \(\beta_{10}=0.950\) (the second and last respectively from left to right), receive from high to very high marginal posterior probability (and similarly for the other replicates, data not shown). In some cases however, some covariates attached with small effects are missed (e.g. Ex4, Figure 6 (b), the last simulated effect which is also the smallest, \(\beta_{16}=0.5\), is not detected). In this situation however the vertical blue solid line indicates that for some replicates, ESS\(i\) is able to assign small values of the marginal posterior probability giving evidence that ESS\(i\) fully explore the whole space of models. Superimposed on all pictures of Figure 5 are the median and interquartile range across replicates of \(p\left(\gamma_{j}=1\left|y\right.\right)\), \(j=1,\ldots,p\), for SSS, red right triangles and vertical red dashed line respectively. We see that there is good agreement between the two algorithms in general, with in addition evidence that ESS\(i\) is able to explore more fully the model space and in particular to find small effects, leading to a posterior model size that is close to the true one. For instance in Ex3, Figure 6 (a), where the last \(30\) covariates accounts for most of \(R_{\gamma}^{2}\), SSS has difficulty to detect \(\left(\beta_{16},\ldots,\beta_{30}\right)\), while in Ex6, it misses \(\beta_{2}=0.112\), the smallest effect, and surprisingly also \(\beta_{4}=-2.595\) assigning a very small marginal posterior probability (and in general for the small effects in most replicates, data not shown). However the most marked difference between ESS\(i\) and SSS is present in Ex5: as for ESS\(i\), SSS misses three effects of “model 1”  but in addition \(\beta_{4}=1\), \(\beta_{7}=-1\) and \(\beta_{8}=1.5\) receive also very low marginal posterior probability, red right triangle, with high variability across replicates, vertical red dashed line. Moreover on the extreme left, as noted before, ESS\(i\) is able to capture the biggest coefficient of “model 2”  while SSS misses completely all contaminated effects. No noticeable differences between ESS\(i\) and SSS are present in Ex1 and Ex2 for the marginal posterior probability, while in Ex4, SSS shows more variability in \(p\left(\gamma_{j}=1\left|y\right.\right)\) (red dashed vertical lines compared to blue solid vertical lines) for some covariates that do receive the highest marginal posterior probability. In contrast to the differences in the marginal posterior probability of inclusion, there is general agreement between the two algorithms with respect to some measures of goodness of fit and stability, see Table 6. Again, not surprisingly, the main difference is seen in Ex5 where ESS\(i\) with \(\tau=1\) reaches a better \(R_{\gamma}^{2}\) both for the maximum and the \(1,000\) largest \(p\left(\gamma\left|y\right.\right)\). SSS shows more stability in all examples, but the last: this was somehow expected since one key features of SSS in its ability to move quickly towards the right model and to persist on it (Hans _et al._, 2007), but a drawback of this is its difficulty to explore far apart models with competing \(R_{\gamma}^{2}\) as in Ex5. Note that ESS\(i\) shows a small improvement of \(R_{\gamma}^{2}\) in all the simulated examples. This is related to the ability of ESS\(i\) to pick up some of the small effects that are missed by SSS, see Figure 6. Finally ESS\(i\) shows a remarkable superiority in terms of computational time especially when the simulated (and estimated) \(p_{\gamma}\) is large (in other simulated examples, data not shown, we found this is always true when \(p_{\gamma}\gtrsim 10\)): the explanation lies in the number of different models SSS and ESS\(i\) evaluate at each sweep. Indeed, SSS evaluates \(p+p_{\gamma}\left(p-p_{\gamma}\right)\), where \(p_{\gamma}\) is the size of the current model, while ESS\(i\) theoretically analyses an equally large number of models, \(pL\), but, when \(p>n\), the actual number of models evaluated is drastically reduced thanks to our FSMH sampler. In only one case SSS beats ESS\(i\) in term of computational time (Ex5), but in this instance SSS clearly underestimates the simulated model and hence performs less evaluations than would be necessary to explore faithfully the model space. In conclusion, we see that the rich porfolio of moves and the use of parallel chains makes ESS robust for tackling complex covariate space as well as competitive against a state of the art search algorithm. ## References Abramowitz, M. and Stegun, I. (1970). _Handbook of Mathematical Functions_. New York: Dover Publications, Inc. Altshuler, D., Brooks, L.D., Chakravarti, A., Collins, F.S., Daly, M.D. and Donnelly, P. (2005). A haplotype map of the human genome. _Nature_, **437**, 1299-1320. Bae, N. and Mallick, B.K. (2004). Gene selection using a two-level hierarchical Bayesian model. _Bioinformatics_, **20**, 3423-3430. Brown, P.J., Vannucci, M. and Fearn, T. (1998). Multivariate Bayesian variable selection and prediction. _J. R. Statist. Soc. B_, **60**, 627-641. Calvo, F. (2005) All-exchange parallel tempering. _J. Chem. Phys._, **123**, 1-7. Chipman, H. (1996). Bayesian variable selection with related predictors. _Canad. J. Statist._, **24**, 17-36. Chipman, H., George, E.I. and McCulloch, R.E. (2001). The practical implementation of Bayesian model selection (with discussion). In _Model Selection_ (P. Lahiri, ed), 66-134. IMS: Beachwood, OH. Clyde, M. and George, E. I. (2004). Model uncertainty. _Statist. Sci._, **19**, 81-94. Cui, W. and George, E.I. (2008). Empirical Bayes vs fully Bayes variable selection. _J. Stat. Plan. Inf._, **138**, 888-900. Dellaportas, P., Forster, J. and Ntzoufras, I. (2002). On Bayesian model and variable selection using MCMC. _Statist. Comp._, **12**, 27-36. Fernández, C., Ley, E. and Steel, M.F.J. (2001). Benchmark priors for Bayesian model averaging. _J. Econometrics_, **75**, 317-343. George, E.I. and McCulloch, R.E. (1993). Variable selection via Gibbs sampling. _J. Am. Statist. Assoc._, **88**, 881-889. George, E.I. and McCulloch, R.E. (1997). Approaches for Bayesian variable selection. _Stat. Sinica_, **7**, 339-373. Geweke, J. (1996). Variable selection and model comparison in regression. In _Bayesian Statistics 5, Proc. 5th Int. Meeting_ (J.M. Bernardo, J.O. Berger, A.P. Dawid and A.F.M. Smith, eds), 609-20. Claredon Press: Oxford, UK. Goswami, G. and Liu, J.S. (2007). On learning strategies for evolutionary Monte Carlo. _Statist. Comp._, **17**, 23-38. Gramacy, R.B, J. Samworth, R.J. and King, R. (2007). Importance Tempering. Tech. rep. Available at: http://arxiv.org/abs/0707.4242 Green, P. and Mira, A. (2001). Delayed rejection in reversible jump Metropolis-Hastings. _Biometrika_, **88**, 1035-1053. Iba, Y. (2001). Extended Ensemble Monte Carlo. _Int. J. Mod. Phys., C_, **12**, 623-656. Hans, C., Dobra, A. and West, M. (2007). Shotgun Stochastic Search for “large \(p\)” regression. _J. Am. Statist. Assoc._, **102**, 507-517. Hubner, N. _et al._ (2005). Integrated transcriptional profiling and linkage analysis for identification of genes underlying disease. _Nat. Genet._, **37**, 243-253. Kohn, R., Smith, M. and Chan, D. (2001). Nonparametric regression using linear combinations of basis functions. _Statist. Comp._, **11**, 313-322. Jasra, A., Stephens, D.A. and Holmes, C. (2007). Population-based reversible jump Markov chain Monte Carlo. _Biometrika_, **94**, 787-807. Liang, F., Paulo, R., Molina, G., Clyde, M.A. and Berger, J.O. (2008). Mixtures of \(g\)-priors for Bayesian variable selection. _J. Am. Statist. Assoc._, **481**, 410-423. Liang, F. and Wong, W.H. (2000). Evolutionary Monte Carlo: application to \(C_{p}\) model sampling and change point problem. _Stat. Sinica_, **10**, 317-342. Liu, J.S. (2001). _Monte Carlo strategies in scientific computations_. Springer: New York. Madigan, D. and York, J. (1995). Bayesian graphical models for discrete data. _Int. Statist. Rev._, **63**, 215-232. Natarajan, R. and McCulloch. (1998). Gibbs sampling with diffuse proper priors: a valid approach to data-driven inference?, _J. Comp. Graph. Statist._, **7**, 267-277. Nott, D.J. and Green, P.J. (2004). Bayesian variable selection and the Swedsen-Wang algorithm. _J. Comp. Graph. Statist._, **13**, 141-157. Roberts, G.O. and Rosenthal, J.S. (2008). Example of adaptive MCMC. Tech. rep. Available at: http://www.probability.ca/jeff/research.html Tierney, L. and Kadane, J.B. (1986). Accurate approximations for posterior moments and marginal densities. _J. Am. Statist. Assoc._, **81**, 82-86. Wilson, M.A., Iversen, E.S., Clyde, M.A., Schmidler, S.C. and Shildkraut, J.M. (2009). Bayesian model search and multilevel inference for SNP association studies. Tech. rep. Available at: http://arxiv.org/abs/0908.1144 Zellner, A. (1986). On assessing prior distributions and Bayesian regression analysis with \(g\)-prior distributions. In _Bayesian Inference and Decision Techniques-Essays in Honour of Bruno de Finetti_ (P.K. Goel and A. Zellner, eds), 233-243. Amsterdam: North-Holland. Zellner, A. and Siow, A. (1980). Posterior odds ratios for selected regression hypotheses. In _Bayesian Statistics, Proc. 1st Int. Meeting_ (J.M. Bernardo, M.H. De Groot, D.V. Lindley and A.F.M. Smith, eds), 585-603. Valencia: University Press. [FIGURE:Ax1.F1][ENDFIGURE] [FIGURE:Ax1.F2][ENDFIGURE] [FIGURE:Ax1.F3][ENDFIGURE] [FIGURE:Ax1.F4][ENDFIGURE] [FIGURE:Ax1.F5][ENDFIGURE] [FIGURE:Ax1.F6][ENDFIGURE] [TABLE:Ax1.T1][ENDTABLE] [TABLE:Ax1.T2][ENDTABLE] [TABLE:Ax1.T3][ENDTABLE] [TABLE:Ax1.T4][ENDTABLE] [TABLE:Ax1.T5][ENDTABLE] [TABLE:Ax1.T6][ENDTABLE]

# Эволюционный стохастический поиск для исследования байесовской модели Леонардо Боттоло Институт математических наук Имперского колледжа Лондона, Великобритания [email protected] Сильвия Ричардсон Центр биостатистики, Имперский колледж, Лондон, Великобритания [email protected] Адрес для переписки: Сильвия Ричардсон, Департамент эпидемиологии и общественного здравоохранения, Имперский колледж, 1 Норфолк Плейс, Лондон, W2 1PG, Великобритания. ##### Аннотация Реализация байесовского выбора переменных для моделей линейной гауссовой регрессии для анализа высокоразмерных наборов данных вызывает активный интерес во многих областях. Чтобы сделать такой анализ оперативным, мы предлагаем новый алгоритм выборки на основе эволюционного метода Монте-Карло и разработанный для работы в рамках парадигмы "большое \(p\), маленькое \(n\)", что позволяет выполнить полноценный байесовский многомерный анализ, например, в генетических/геномных экспериментах. Представлены два примера реальных данных в геномике, продемонстрировавшие эффективность алгоритма в пространстве до \(10,000\) коэффициентов. Наконец, методология сравнивается с недавно предложенными алгоритмами поиска в обширном исследовании на основе моделирования. _Ключевые слова_: Эволюционный Монте-Карло; Быстрые алгоритмы Скан-Метрополиса-Гастингса; Линейные гауссовы регрессионные модели; Выбор переменных. ## 1 Введение Эта работа является вкладом в методологию байесовского выбора переменных для моделей линейной гауссовской регрессии, важной проблемы, которая была широко обсуждена как с теоретической, так и с практической точек зрения (см. Chipman _et al._, 2001 и Clyde и George, 2004 для обзора литературы). Недавно были достигнуты прогресс в двух направлениях: раскрытие теоретических свойств различных выборов структуры априорного распределения для коэффициентов регрессии (Fernández _et al._, 2001; Liang _et al._, 2008) и предложение алгоритмов, которые могут исследовать огромное пространство модели, состоящее из всех возможных подмножеств, когда имеется большое количество ковариат (Kohn _et al._, 2001; Dellaportas _et al._, 2002; Hans _et al._, 2007), используя методы МСМС или другие алгоритмы поиска. В этой статье мы предлагаем новый алгоритм выборки для реализации модели выбора переменных, основанный на концепции эволюционного монте-карло (Liang and Wong, 2000; Jasra et al., 2007; Wilson et al., 2009) с целью преодоления известных трудностей, с которыми сталкиваются СМС-сэмплеры в пространстве моделей высокой размерности и многоэкстремальности: перечисление пространства моделей становится быстро невозможным, даже при умеренном числе объясняющих переменных. Чтобы байесовский подход мог быть оперативным, он должен сопровождаться алгоритмом, который выбирает индикаторы выбранных подмножеств объясняющих переменных, вместе с другими параметрами, которые не были интегрированы. Наш новый алгоритм поиска по пространству моделей имеет много общих особенностей, которые представляют интерес _per se_ и могут быть легко сочетаны с любой формулировкой априорных распределений для дисперсионно-ковариационных коэффициентов регрессии. Мы иллюстрируем это, применяя \(g\)-приоры для коэффициентов регрессии, а также независимые априорные распределения: в обоих случаях принятая нами формулировка является общей и позволяет задать дополнительный уровень иерархии для априорных распределений коэффициентов регрессии, если это требуется. Статья имеет следующую структуру. В разделе 2 представлено введение в байесовский выбор переменных, кратко обзорно описываются альтернативные априорные спецификации для коэффициентов регрессии, а именно \(g\)-априоры и независимые априоры. Раздел 3 посвящен описанию нашего MCMC-сэмплера, который использует широкий набор шагов, включая два предложенных новых. Раздел 4 демонстрирует хорошую производительность нашего нового алгоритма MCMC на различных реальных и симулированных примерах с разными структурами предикторов. В разделе 4.2 мы дополняем результаты исследования симуляции, сравнивая наш алгоритм с недавним алгоритмом стохастического поиска Shotgun из работы Ханса _и др._ (2007). Наконец, раздел 5 содержит некоторые заключительные замечания. ## 2 Фон ### Выбор переменных Пусть \(y=\left(y_{1},\ldots,y_{n}\right)^{T}\) - последовательность \(n\) наблюдаемых откликов, а \(x_{i}=\left(x_{i1},\ldots,x_{ip}\right)^{T}\) - вектор предикторов для \(y_{i}\), \(i=1,\ldots,n\), размерности \(p\times 1\). Кроме того, пусть \(X\) - это матрица размером \(n\times p\) с \(i\)-ой строкой \(x_{i}^{T}\). Гауссовская линейная модель может быть описана уравнением \[y=\alpha 1_{n}+X\beta+\varepsilon,\] где \(\alpha\) является неизвестной константой, \(1_{n}\) - столбцовый вектор из единиц, \(\beta=\left(\beta_{1},\ldots,\beta_{p}\right)^{T}\) - \(p\times 1\) вектор неизвестных параметров и \(\varepsilon\sim N\left(0,\sigma^{2}I_{n}\right)\). Предположим, что кто-то хочет построить модель для отношения между \(y\) и подмножеством \(x_{1},\ldots,x_{p}\), но существует неопределенность относительно того, какое подмножество использовать. Следуя обычному соглашению рассматривать только модели, содержащие перехват \(\alpha\), эта проблема, известная как выбор переменных или выбор подмножества, особенно интересна, когда \(p\) велико и требуются эффективные модели, содержащие только несколько предикторов для их интерпретируемости. С байесовской точки зрения проблема решается путем установления постоянной априорной плотности на \(\alpha\) и априорного распределения на \(\beta\), которое зависит от скрытого бинарного вектора \(\gamma=\left(\gamma_{1},\ldots,\gamma_{p}\right)^{T}\), где \(\gamma_{j}=1\), если \(\beta_{j}\neq 0\), и \(\gamma_{j}=0\), если \(\beta_{j}=0\), \(j=1,\ldots,p\). Общее количество возможных моделей, определенных через \(\gamma\), растет экспоненциально с \(p\), и выбор лучшей модели, предсказывающей \(y\), эквивалентен нахождению одной из \(2^{p}\) подмножеств, составляющих пространство моделей. Учитывая скрытую переменную \(\gamma\), гауссовская линейная модель может быть записана как \[y=\alpha 1_{n}+X_{\gamma}\beta_{\gamma}+\varepsilon,\] (1) где \(\beta_{\gamma}\) - ненулевой вектор коэффициентов, извлеченных из \(\beta\), \(X_{\gamma}\) - матрица дизайна размерности \(n\times p_{\gamma}\), \(p_{\gamma}\equiv\gamma^{T}1_{p}\), столбцы которой соответствуют \(\gamma_{j}=1\). Мы предполагаем, что, за исключением интерцепта \(\alpha\), \(x_{1},\ldots,x_{p}\) не содержит переменных, которые бы были включены в каждую возможную модель, и что столбцы матрицы дизайна были отцентрированы средним значением \(0\). Рекомендуется обрабатывать перехват отдельно и присвоить ему постоянное априорное значение: \(p(\alpha) \propto 1\), Фернандес _et al._ (2001). Когда связан с латентной переменной \(\gamma\), сопряженная априорная структура \(\left(\beta_{\gamma},\sigma^{2}\right)\) подчиняется нормально-инверсно-гамма распределению. \[\ p\left(\beta_{\gamma}\left|\gamma,\sigma^{2}\right.\right)=N\left(m_{\gamma}, \sigma^{2}\Sigma_{\gamma}\right)\ \] (2) \[ p\left(\sigma^{2}\left|\gamma\right.\right)=p\left(\sigma^{2}\right)=InvGa \left(a_{\sigma},b_{\sigma}\right)\tag{3} \] c \(a_{\sigma},b_{\sigma}>0\). Некоторые руководства по выбору значений гиперпараметров \(a_{\sigma}\) и \(b_{\sigma}\) представлены в работе Кона _et al._ (2001), в то время как случай \(a_{\sigma}=b_{\sigma}=0\) соответствует априорной плотности Джеффриса для дисперсии ошибки, \(p\left(\sigma^{2}\right)\propto\sigma^{-2}\). Учитывая (1), (2), (3) и априорную спецификацию для \(\alpha\), совместное распределение всех переменных (с учетом дальнейших условий условной независимости) может быть записано как \[p\left(y,\gamma,\alpha,\beta_{\gamma},\sigma^{2}\right)=p\left(y\left|\gamma, \alpha,\beta_{\gamma},\sigma^{2}\right.\right)p\left(\alpha\right)p\left(\beta _{\gamma}\left|\gamma,\sigma^{2}\right.\right)p\left(\sigma^{2}\right)p\left( \gamma\right).\] (4) Основным преимуществом конъюгатной структуры (2) и (3) является аналитическая прослеживаемость маргинальной вероятности независимо от спецификации матрицы ковариации априорного распределения \(\Sigma_{\gamma}\): \[\int p\left(y\left|\gamma,\alpha,\beta_{\gamma},\sigma^{2}\right.\right)p\left(\alpha\right)p\left(\beta_{\gamma}\left|\gamma,\sigma^{2}\right.\right)p\left(\sigma^{2}\right)d\alpha\text{\/{}\/}d\beta_{\gamma}d\sigma^{2}\] (5) \[\propto \left|X_{\gamma}^{T}X_{\gamma}+\Sigma_{\gamma}^{-1}\right|^{-1/2} \left|\Sigma_{\gamma}\right|^{-1/2}\left(2b_{\sigma}+S\left(\gamma\right) \right)^{-\left(2a_{\sigma}+n-1\right)/2},\] где \(S(\gamma)=C-M^{T}K_{\gamma}^{-1}M\), где \(C=(y-\bar{y}_{n})^{T}(y-\bar{y}_{n})+m_{\gamma}^{T} \Sigma_{\gamma}^{-1}m_{\gamma}\), \(M=X_{\gamma}^{T}(y-\bar{y}_{n})+\Sigma_{\gamma}^{-1}m_{\gamma}\) и \(K_{\gamma}=X_{\gamma}^{T}X_{\gamma}+\Sigma_{\gamma}^{-1}\) (Brown _et al._, 1998). Хотя среднее значение априорного распределения (2) обычно устанавливается равным нулю, \(m_{\gamma}=0\), что является нейтральным выбором (Chipman _et al._, 2001; Clyde and George, 2004), спецификация априорной ковариационной матрицы \(\Sigma_{\gamma}\) приводит к как минимум двум различным классам априорных распределений: •Когда \(\Sigma_{\gamma}=gV_{\gamma}\), где \(g\) является скаляром, а \(V_{\gamma}=\left(X_{\gamma}^{T}X_{\gamma}\right)^{-1}\), это воспроизводит ковариационную структуру функции правдоподобия, приводящую к так называемым \(g\)-prior, сначала предложенным Зеллнером (1986 г.). * •Когда \(\Sigma_{\gamma}=cV_{\gamma}\), а \(V_{\gamma}=I_{p_{\gamma}}\), компоненты \(\beta_{\gamma}\) условно независимы, и матрица апостериорной ковариации смещается в сторону случая независимости. Мы будем использовать обозначение \(\Sigma_{\gamma}=\tau V_{\gamma}\), так как мы хотим объединить оба примера априорной информации. Таким образом, в случае с \(g\)-prior, \(\Sigma_{\gamma}=\tau\left(X_{\gamma}^{T}X_{\gamma}\right)^{-1}\), а в случае независимости, \(\Sigma_{\gamma}=\tau I_{p_{\gamma}}\). Мы будем называть \(\tau\) _коэффициентом выбора переменных_ по причинам, которые станут ясны в следующем разделе. Чтобы завершить предыдущую спецификацию в (4), необходимо определить \(p\left(\gamma\right)\). Полное обсуждение альтернативных априорных распределений на пространстве моделей можно найти в работе Чипмена (1996) и Чипмана и др. (2001). Здесь мы принимаем бета-биномиальное априорное распределение, иллюстрированное в работе Кона и др. (2001). \[p(\gamma)=\int p(\gamma|\omega)p(\omega)d\omega=\frac{B(p_{\gamma}+a_{\omega},p-p_{\gamma}+b_{\omega})}{B(a_{\omega},b_{\omega})}\] (6) при \(p_{\gamma}\equiv\gamma^{T}1_{p}\), выбор \(p\left(\gamma\left|\omega\right.\right)=\omega^{p_{\gamma}}\left(1-\omega \right)^{p-p_{\gamma}}\) неявно приводит к биномиальному априорному распределению на размер модели, а \(p\left(\omega\right)=\omega^{a_{\omega}-1}\left(1-\omega\right)^{b_{\omega}-1} /B\left(a_{\omega},b_{\omega}\right)\). Гиперпараметры \(a_{\omega}\) и \(b_{\omega}\) могут быть выбраны после установления \(E\left(p_{\gamma}\right)\) и \(V\left(p_{\gamma}\right)\). В рамках «большого \(p\), маленького \(n\)» подхода, чтобы гарантировать разреженные модели регрессии, где \(p_{\gamma}\ll p\), рекомендуется центрировать априорное распределение для размера модели за пределами количества наблюдений. ### Априорные вероятности для коэффициента выбора переменных \(\tau\) #### 2.2.1 \(g\)-предпочтения Известно, что приоры \(g\) обладают двумя привлекательными свойствами. Во-первых, они обладают автоматической функцией масштабирования (Chipman _et al._, 2001; Kohn _et al._, 2001). В отличие от независимых приоров, влияние \(V_{\gamma}=I_{p_{\gamma}}\) на апостериорное распределение зависит от относительного масштаба \(X\), и рекомендуется стандартизация матрицы плана до единиц стандартного отклонения. Однако это не всегда лучшая процедура, когда \(X\) возможно искажено, или когда столбцы \(X\) не определены в единицах измерения. Второе свойство, делающее приоры \(g\) особенно привлекательными, - это относительно простая структура условного распределения (5) относительно константы \(\tau\), которая становится+ \[\propto\left(1+\tau\right)^{-p_{\gamma}/2}\left(2b_{\sigma}+S\left(\gamma \right)\right)^{-\left(2a_{\sigma}+n-1\right)/2},\] (7) где, если \(m_{\gamma}=0\), \(S\left(\gamma\right)=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)- \frac{\tau}{1+\tau}\left(y-\bar{y}_{n}\right)^{T}X_{\gamma}\left(X_{\gamma}^{T }X_{\gamma}\right)^{-1}X_{\gamma}^{T}\left(y-\bar{y}_{n}\right)\). По вычислительным причинам, объясненным в следующем разделе, мы предполагаем, что (7) всегда определено: так как мы вычисляем \(S\left(\gamma\right)\) с использованием QR-разложения регрессии \(\left(X_{\gamma},y-\bar{y}_{n}\right)\) (Brown _et al._, 1998), когда \(n\leq p_{\gamma}\), \(S\left(\gamma\right)=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)/ \left(1+\tau\right)\). Несмотря на простоту (7), выбор постоянной \(\tau\) для \(g\)-гиперпараметров является сложным, см. Fernández _et al._ (2001), Cui and George (2008) и Liang _et al._ (2008). Исторически первая попытка построения комплексного байесовского анализа, включающего априорное распределение на \(\tau\), уходит корнями в работу Зеллнера и Сиао (1980), где адаптивность данных степени сжатия адаптируется к различным сценариям лучше, чем при предположении стандартных фиксированных значений. Априорные распределения Зеллнера-Сиао, в дальнейшем Z-S, могут рассматриваться как смесь \(g\)-априорных распределений и обратного гамма-распределения на \(\tau\), \(\tau\sim InvGa(1/2,n/2)\), что приводит к Для перевода данного уравнения на русский язык, необходимо сохранить формулу: \[\displaystyle p\left(\beta_{\gamma}\left|\gamma,\sigma^{2}\right.\right)\propto\int N\left(0 ,\sigma^{2}\tau\left(X_{\gamma}^{T}X_{\gamma}\right)^{-1}\right)p\left(\tau \right)d\tau.\] (8) Лианг _et al._ (2008) детально анализируют Z-S априорные распределения, указывая на разнообразие теоретических свойств. С вычислительной точки зрения, с Z-S априорными распределениями, маргинальная вероятность \(p\left(y\left|\gamma\right.\right)=\int p\left(y\left|\gamma,\tau\right.\right )p\left(\tau\right)d\tau\) больше не доступна в закрытом виде, что является преимуществом для быстрого выполнения стохастического поиска (Chipman _et al._, 2001). Несмотря на то, что Z-S априорные распределения не требуют калибровки, и можно получить аппроксимацию Лапласа (Tierney and Kadane, 1986), см. Приложение A.2, они никогда не стали так популярными, как \(g\)-априорные распределения с соответствующим постоянным значением для \(\tau\). Для альтернативных априорных распределений см. также Cui and George (2008) и Liang _et al._ (2008). #### 2.2.2 Независимые априорные вероятности Когда все переменные определены на одинаковой шкале, независимые априорные представляют привлекательную альтернативу для \(g\)-априорных. Функция правдоподобия, интегрированная по \(\alpha\), \(\beta_{\gamma}\) и \(\sigma^{2}\), принимает вид \[p\left(y\left|\gamma\right.\right)\propto\tau^{-p_{\gamma}/2} \left|X_{\gamma}^{T}X_{\gamma}+\tau I_{p_{\gamma}}\right|^{-1/2}\left(2b_{ \sigma}+S\left(\gamma\right)\right)^{-\left(2a_{\sigma}+n-1\right)/2},\] (9) где, если \(m_{\gamma}=0\), \(S\left(\gamma\right)=\left(y-\bar{y}_{n}\right)^{T}\left(y-\bar{y}_{n}\right)- \left(y-\bar{y}_{n}\right)^{T}X_{\gamma}\left(X_{\gamma}^{T}X_{\gamma}+\tau I_ {p_{\gamma}}\right)^{-1}X_{\gamma}^{T}\left(y-\bar{y}_{n}\right)\). Обратите внимание, что (9) для вычисления требует больше ресурсов, чем (7) из-за дополнительного оператора определителя. Geweke (1996) предлагает зафиксировать различное значение \(\tau_{j}\), \(j=1,\ldots,p\), основываясь на идее "существенного значимого определителя" \(\Delta X_{j}\) относительно \(\Delta y\). Однако общей практикой является стандартизация предикторных переменных, принимая \(\tau=1\), чтобы расставить соответствующее априорное распределение на разумные значения коэффициентов регрессии (Ханс и др., 2007). Другой подход, иллюстрируемый в работе Бэ и Маллика (2004), заключается в присвоении априорного распределения \(\tau_{j}\) без стандартизации предикторов. Безотносительно к предварительной спецификации для \(\tau\), используя QR-разложение для подходящего преобразования \(X_{\gamma}\) и \(y-\bar{y}_{n}\), совместная вероятность (9) всегда определена. ## 3 MCMC семплер В данном разделе мы предлагаем новый алгоритм выборки, который преодолевает известные трудности, с которыми сталкиваются схемы MCMC при попытке выборки многомодального пространства высокой размерности. Мы обсуждаем объединенный подход к общему случаю, в котором задается гипераприор на коэффициент выборки переменных \(\tau\). Это включает \(g\)-prior и независимую структуру априори, а также случай фиксированного \(\tau\), если используется априорное распределение типа "точечная масса". Многомодальность пространства моделей является известной проблемой в отборе переменных, и в последние несколько лет было предложено несколько способов решения этой проблемы. Liang и Wong (2000) предлагают расширение параллельного каления, называемое Эволюционным Монте-Карло (EMC), в дальнейшем - Nott and Green, N&G (2004) представляют схему выборки, вдохновленную алгоритмом Свендсена-Ванга, в то время как Jasra _et al._ (2007) расширяют методы EMC до алгоритмов с переменной размерностью. Наконец, Hans _et al._ (2007) предлагают новый стохастический поисковый алгоритм SSS для исследования моделей, находящихся в одном окрестности, с целью быстрого нахождения лучшей комбинации предикторов, когда \(p>n\). Мы предлагаем решить проблему, связанную с многомодальностью пространства моделей (и зависимостью между \(\gamma\) и \(\tau\)), следуя принципам EMC, применяя соответствующие стратегии параллельного отжига напрямую к \(p\left(y\left|\gamma,\tau\right.\right)\). Основная идея параллельного отжига, или PT в дальнейшем, заключается в уменьшении зависимости функции от ее параметров путем добавления дополнительного параметра, называемого "температурой". Несколько параллельных Марковских цепей, называемых "популяцией" цепей, запускаются параллельно, при этом каждой цепи присваивается отдельная температура, их состояние временно обменивается на каждой итерации с использованием вероятностного механизма, и фиксируется скрытый бинарный вектор \(\gamma\) нагретой цепи. Различные температуры имеют эффект выравнивания правдоподобия. Это гарантирует, что апостериорное распределение не застревает в локальных модах и что алгоритм эффективно перемешивает цепи, поскольку каждая цепь постоянно пытается передать информацию о своем состоянии другим цепям. EMC расширяет эту идею, объединяя положительные свойства PT и генетических алгоритмов в рамках схемы МСМС. Так как \(\beta\) и \(\sigma^{2}\) интегрируются, нужно выбрать только два параметра: скрытый бинарный вектор и коэффициент выбора переменных. В данной настройке следует рассмотреть полные условия \[\left[p(\gamma_{l}|\cdots)\right]^{1/t_{l}}\propto\left[p(y|\gamma_{l},\tau)\right]^{1/t_{l}}\left[p(\gamma_{l})\right]^{1/t_{l}}\] (10) \[p\left(\tau\left|\cdots\right.\right)\propto\prod\nolimits_{l=1}^{L}\left[p \left(y\left|\gamma_{l},\tau\right.\right)\right]^{1/t_{l}}p\left(\tau\right),\] (11) \[p\left(\tau\left|\cdots\right.\right)\propto\prod\nolimits_{l=1}^{L}\left[p \left(y\left|\gamma_{l},\tau\right.\right)\right]^{1/t_{l}}p\left(\tau\right),\] (11) где \(L\) - количество цепей в популяции, а \(t_{l}\), \(1=t_{1}<t_{2}<\cdots<t_{L}\), - температура, присоединенная к \(l\)-й цепи, в то время как популяция \(\bm{\gamma}\) соответствует набору цепей, которые одновременно сохраняются. Условия сходимости алгоритмов EMC хорошо изучены и иллюстрированы, например, в работе Jasra _et al._ (2007). На каждом проходе нашего алгоритма сначала популяция \(\bm{\gamma}\) из (10) обновляется с использованием различных движений, вдохновленных генетическими алгоритмами: «локальные движения», обычное обновление Метрополиса-Гастингса или Гиббса на каждой цепи; и «глобальные движения», которые включают: i) выбор цепей для обмена, основанный на некоторых вероятностных мерах расстояния между ними; ii) оператор кроссовера, то есть частичный обмен текущим состоянием между разными цепями; iii) оператор обмена, полный обмен состояниями между цепями. Как локальные, так и глобальные движения важны, хотя глобальные движения критичны, потому что позволяют алгоритму переходить от одного локального режима к другому. По окончании обновления \(\bm{\gamma}\), \(\tau\) выбирается с использованием (11). Реализация EMC, которую мы предлагаем в этой статье, включает несколько новых аспектов: использование широкого спектра действий, включая два новых действия, локальное действие, основанное на быстром алгоритме Metropolis-Hastings для сканирования, особенно подходящее, когда \(p\) является большим, а также смелое глобальное действие, которое использует корреляционную структуру предикторов. Кроме того, мы разработали эффективную схему настройки размещения температуры, которая использует эффективный обмен между цепями. Еще одной новой особенностью является использование адаптивных предложений Metropolis-within-Gibbs для обновления \(\tau\), так как полное условное распределение (11) недоступно в явном виде. ### EMC сэмплер для \(\bm{\gamma}\) В следующем мы только наметим обоснование всех шагов, которые мы нашли полезными для реализации, и обсудим дополнительные преимущества новых конкретных шагов в разделе 4.1. Для парадигмы "больших \(p\), малых \(n\)" и комплексных пространств предсказателей мы считаем, что использование широкого портфеля шагов необходимо и обеспечивает лучшую гарантию смешивания. С нотационной точки зрения мы будем использовать двойные индексы \(\gamma_{l,j}\), \(l=1,\ldots,L\) и \(j=1,\ldots,p\) для обозначения \(j\)-го скрытого бинарного индикатора в \(l\)-ой цепи. Более того, мы обозначаем \(\gamma_{l}=\left(\gamma_{l,1},\ldots,\gamma_{l,p}\right)^{T}\) вектором бинарных индикаторов, характеризующих состояние \(l\)-ой цепи популяции \(\bm{\gamma}=\left(\gamma_{1},\ldots,\gamma_{L}\right)\). #### Локальные перемещения и сэмплер Метрополиса-Гастингса с быстрым сканированием Учитывая \(\tau\), мы сначала попробовали простую идею MC\({}^{3}\) Мэдигана и Йорка (1995), также используемую Брауном и др. (1998), где используются операции добавления/удаления и замены для обновления скрытого бинарного вектора \(\gamma_{l}\). Для операции добавления/удаления одна из \(p\) переменных выбирается случайным образом, и если значение скрытого бинарного вектора равно \(0\), предлагается новое значение \(1\) или наоборот. Однако, когда \(p\gg p_{\gamma_{l}}\), где \(p_{\gamma_{l}}\) - размер текущей модели для \(l\)-ой цепи, количество прогонов, необходимых для случайного выбора бинарного индикатора со значением \(1\), следует геометрическому распределению с вероятностью \(p_{\gamma}/p\), которая гораздо меньше, чем \(1-p_{\gamma}/p\) для выбора бинарного индикатора со значением \(0\). Следовательно, алгоритм большую часть времени тратит на попытки добавить, а не удалить переменную. Заметим, что эта проблема также влияет на алгоритмы типа RJ (Деллапортас и др., 2002). С другой стороны, сэмплирование Гиббса (Джордж и Маккаллох, ГиМак в дальнейшем, 1993) не подвержено этой проблеме, так как состояние \(l\)-ой цепи обновляется путем сэмплирования из \[\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}\propto\exp\left\{\left(\log p\left(y\left|\gamma_{l,j}^{\left(1 \right)},\tau\right.\right)+\log p\left(\gamma_{l,j}=1\left|\gamma_{l,j^{-}} \right.\right)\right)/t_{l}\right\},\] (12) где \(\gamma_{l,j^{-}}\) обозначает для \(l\)-й цепи все переменные, кроме \(j\)-й, \(j=1,\ldots,p\) и \(\gamma_{l,j}^{\left(1\right)}=\left(\gamma_{l,1},\ldots,\gamma_{l,j-1},\gamma_ {l,j}=1,\gamma_{l,j+1},\ldots,\gamma_{l,p}\right)^{T}\). Основная проблема, связанная с методом Гиббса, заключается в большом количестве моделей, которые оцениваются, если в каждом проходе применяется полный цикл метода Гиббса или любая перестановка индексов. Каждая модель требует прямой оценки, или по крайней мере обновления, трудоемкой величины \(S\left(\gamma\right)\), уравнение (7) или (9), что практически делает невозможным полное полагание только на сэмплер Гиббса, когда \(p\) очень велико. Однако, как было отмечено Коном и др. (2001), является расточительным оценивать все \(p\) обновлений в цикле, потому что если \(p_{\gamma_{l}}\) намного меньше, чем \(p\) и при условии, что \(\gamma_{l,j}=0\), вероятно, что выбранное значение для \(\gamma_{l,j}\) снова будет \(0\). Когда \(p\) большое, мы рассматриваем новую схему сканирования Метрополиса-Гастингса с быстрым сканированием (FSMH), специализированную для EMC/PT, вместо стандартных операций добавления/удаления и замены MC\({}^{3}\). Эта схема является вычислительно менее затратной, чем полная сэмплирование Гиббса по всем \(\gamma_{l,j}\) и не страдает от проблем, указанных ранее для MC\({}^{3}\) и алгоритмов типа RJ, когда \(p\gg p_{\gamma_{l}}\). Идея FSMH состоит в использовании дополнительного шага принятия/отклонения (который очень быстро вычисляется) для выбора количества индексов, на которых будет выполнен шаг Гиббса. Новизна нашего алгоритма FSMH заключается в том, что дополнительная вероятность, используемая на этом шаге принятия/отклонения, основана не только на текущем размере модели цепи \(p_{\gamma_{l}}\), но также на температуре \(t_{l}\), присоединенной к \(l\)-ой цепи. Поэтому наша цель - сэкономить вычислительное время в случае большого \(p\), когда несколько цепей симулируются параллельно, и найти альтернативную схему для полного сэмплирования Гиббса. Для сокращения вычислительного времени наша стратегия заключается в оценке времени затрат на вычисление маргинальной вероятности (5) не более, чем примерно \(\left\lfloor\tilde{\theta}_{l,\bullet}^{(1)}\left(1/t_{l}\right)\left(p-p_{\gamma}\right)+\tilde{\theta}_{l,\bullet}^{(0)}\left(1/t_{l}\right)p_{\gamma}\right\rfloor\) раз в цикле \(l\)-ой цепи (при условии достижения сходимости), где \(\tilde{\theta}_{l,\bullet}^{(1)}\left(1/t_{l}\right)\) - вероятность выбора переменной для добавления на шаге принятия/отклонения, которая зависит от текущего размера модели \(p_{\gamma_{l}}\) и температуры \(t_{l}\), и аналогично для \(\tilde{\theta}_{l,\bullet}^{(0)}\left(1/t_{l}\right)\) (\(\left\lfloor\cdot\right\rfloor\) обозначает целую часть). Поскольку для цепей с более низкими температурами \(\tilde{\theta}_{l,\bullet}^{(0)}\left(1/t_{l}\right)\gg\tilde{\theta}_{l, \bullet}^{(1)}\left(1/t_{l}\right)\), алгоритм предлагает обновить _почти все_ бинарные индикаторы со значением \(1\), в то время как группа из примерно \(\left\lfloor\tilde{\theta}_{l,\bullet}^{(1)}\left(1/t_{l}\right)\left(p-p_{ \gamma}\right)\right\rfloor\) бинарных индикаторов со значением \(0\) выбирается случайным образом для обновления. При более высоких температурах, поскольку \(\tilde{\theta}_{l,\bullet}^{(0)}\) и \(\tilde{\theta}_{l,\bullet}^{(1)}\) становятся более похожими, количество моделей, оцениваемых в цикле, увеличивается, поскольку обновляются гораздо больше бинарных индикаторов со значением \(0\). Полные подробности схемы FSMH приведены в Приложении A.1, а оценка и сравнение с MC\({}^{3}\), встроенным в EMC, представлены в разделах 4.1 и 4.2. #### Глобальное перемещение: оператор кроссовера Первый этап данного хода состоит в выборе пары цепочек \(\left(l,r\right)\), на которых будет производиться операция. Сначала мы вычисляем вероятность, равную весу "пробоя", \(p_{t}\left(\gamma_{l}\left|\tau\right.\right)=\exp\left\{f\left(\gamma_{l} \left|\tau\right.\right)/t\right\}/F_{t}\), где \(f\left(\gamma_{l}\left|\tau\right.\right)=\log p\left(\gamma_{l}\left|y,\tau \right.\right)+\log p\left(\gamma_{l}\right)\) - это логарифмическое преобразование полного условного распределения (10), предполагая \(t_{l}=1\)\(\forall l\), \(l=1,\ldots,L\), а \(F_{t}=\sum_{l=1}^{L}\exp\left\{f\left(\gamma_{l}\left|\tau\right.\right)/t\right\}\) для некоторой конкретной температуры \(t\), а затем ранжируем все цепочки в соответствии с этим. Мы используем нормализованные веса Больцмана, чтобы увеличить вероятность того, что две выбранные цепочки приведут к новой конфигурации популяции с более высокой апостериорной вероятностью после скрещивания. Мы называем этот первый шаг "оператором выбора". Предположим, что затем из выбранных цепей генерируются два новых скрытых бинарных вектора согласно некоторому оператору скрещивания, описанному ниже. Новая предлагаемая популяция цепей. \(\bm{\gamma}^{\prime}=\left(\gamma_{1},\ldots,\gamma_{l}^{\prime},\ldots,\gamma _{r}^{\prime},\ldots,\gamma_{L}\right)\) принимается с вероятностью \[ \alpha(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime})=\min\left\{1, \frac{\exp\left\{f\left(\gamma_{l}^{\prime}|\tau\right)/t_{l}+f (\gamma_{r}^{\prime}|\tau)/t_{r}\right\}}{\exp\left\{f (\gamma_{l}|\tau)/t_{l}+f(\gamma_{r}|\tau)\right\}/t_{r}}\frac{Q_{t}(\bm{\gamma}^{\prime}\to \bm{\gamma}|\tau)}{Q_{t}(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}|\tau)}\right\},\ (13) \] где \(Q_{t}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\left|\tau\right.\right)\) является вероятностью предложения, см. Liang and Wong (2000). В следующем мы предположим, что на каждой итерации EMC случайным образом выбираются четыре различных оператора скрещивания: скрещивание с одной точкой, равномерное скрещивание, адаптивное скрещивание (Liang and Wong, 2000) и новое блочное скрещивание. Из этих четырех операторов равномерное скрещивание, "перемешивающее" бинарные индикаторы по всем выбранным цепям, ожидается иметь низкую степень принятия, но способность действительно проникать в области низкой апостериорной вероятности. Блочное скрещивание в основном пытается обменять группу сильно коррелированных переменных и может быть рассмотрено как многоточечное скрещивание, где точки скрещивания не являются случайными, а определены структурой корреляции между ковариатами. На практике блочное скрещивание определяется следующим образом: случайным образом выбирается одна переменная с вероятностью \(1/p\), затем вычисляется попарная корреляция \(\rho\left(X_{j},X_{j^{\prime}}\right)\) между \(j\)-м выбранным предиктором и каждой оставшейся ковариатой \(j^{\prime}=1,\ldots,p\), \(j^{\prime}\neq j\). Затем для блочного скрещивания мы сохраняем все ковариаты с положительной (отрицательной) попарной корреляцией с \(X_{j}\), так чтобы \(\left|\rho\left(X_{j},X_{j^{\prime}}\right)\right|\geq\rho_{0}\). Порог \(\rho_{0}\) выбирается с учетом конкретной задачи, но мы фиксируем его равным \(0.25\). Оценка блочного скрещивания и сравнение с другими операторами скрещивания представлены на примере реальных данных в разделе 4.1. #### Глобальное перемещение: оператор обмена Оператор обмена можно рассматривать как чрезвычайный случай оператора скрещивания, где первая предложенная цепочка получает весь второй состояние цепочки \(\gamma_{l}^{\prime} = \gamma_{r}\), и наоборот. Чтобы достичь хорошей скорости принятия, оператор обмена обычно применяется к соседним цепям в температурной лестнице, что ограничивает его способность для смешивания. Для достижения лучшего смешивания мы реализовали два разных подхода: первый основан на работе Ясра _et al._ (2007) и связанной идее отложенного отклонения (Грин и Мира, 2001); второй, более решительный "полный обмен" основан на предварительном расчете всех \(L\left(L-1\right)/2\) коэффициентов принятия обмена между парами всех цепочек (Кальво, 2005). Полная соответствующая информация представлена в приложении A.1. Оба этих смелых хода хорошо работают в приложениях с реальными данными, см. Раздел 4.1, и в моделируемых примерах, см. Раздел 4.2, что способствует эффективности алгоритма. #### Размещение температуры Как отмечено Госвами и Лю (2007), размещение температурной лестницы является наиболее важным компонентом методов МСМП на основе популяции. Мы предлагаем процедуру размещения температуры, которая имеет преимущество простоты, сохраняя при этом хорошую точность. Во-первых, мы фиксируем размер \(L\) популяции. При этом мы руководствуемся несколькими соображениями: сложность проблемы, то есть \(E\left(p_{\gamma}\right)\), размер данных и вычислительные ограничения. Мы провели эксперименты и рекомендуем фиксировать \(L\geq 3\). Несмотря на то, что некоторые из смоделированных примеров имели \(p_{\gamma}\simeq 20\) (раздел 4.2), мы обнаружили, что \(L=5\) было достаточно для получения хороших результатов. В наших примерах с реальными данными (раздел 4.1) мы использовали \(L=4\) на основе некоторых предварительных знаний о \(E\left(p_{\gamma}\right)\). Во-вторых, мы фиксируем на начальном этапе температурную лестницу согласно геометрической шкале, такой что \(t_{l+1}/t_{l}=b\), \(b>1\), \(l=1,\ldots,L\) с относительно большим значением \(b\), например \(b=4\). Для дальнейшей настройки температурной лестницы мы применяем стратегию, основанную только на мониторинге коэффициента принятия оператора обмена с отсрочкой с целью достижения значения \(0.5\). Подробности реализации оставлены в Приложении A.1. ### Адаптивный Метрополис-внутри-Гиббса для \(\tau\) Различные стратегии могут быть использованы для избегания необходимости выборки из апостериорного распределения коэффициента выбора переменных \(\tau\). Самый простой способ - интегрировать его с помощью аппроксимации Лапласа (Tierney and Kadane, 1986) или использовать численное интегрирование, такое как квадратура на бесконечном интервале. Мы не преследуем эти стратегии, и причины могут быть суммированы следующим образом. Интегрирование \(\tau\) в населении неявно подразумевает, что каждая цепочка имеет свое значение коэффициента выбора переменных \(\tau_{l}\) (и латентного бинарного вектора \(\gamma_{l}\)). В этом формате могут возникнуть две неприятные ситуации: во-первых, при применении аппроксимации Лапласа, _равновесие_ в пространстве произведений сложно достичь, потому что апостериорное распределение \(\gamma_{l}\) зависит, через предельное понимание, полученное с использованием аппроксимации Лапласа, от _значения цепочки_ для апостериорного режима \(\tau_{l}\), \(\hat{\tau}_{\gamma_{l}}\) (подробности в приложении A.2). Поскольку сила \(X_{\gamma_{l}}\) для предсказания ответа ослаблена для цепочек, подключенных к высоким температурам, оказывается, что для этих цепочек \(\hat{\tau}_{\gamma_{l}}\) скорее всего будет близким к нулю. Когда коэффициент выбора переменных очень мал, зависимость предельного понимания от \(X_{\gamma_{l}}\) уменьшается еще больше, см., например, (7), и цепочки, присоединенные к высоким температурам, будут испытывать очень неустойчивое поведение, что делает сходимость в пространстве произведений сложной для достижения. Кроме того, если применяется автоматическая настройка лестницы температур, цепочки будут все больше размещаться на более близком расстоянии в лестнице температур для балансировки низкой степени принятия глобальных шагов, что противоречит цели EMC. В этой статье сходимость достигается в пространстве произведений \(\prod\nolimits_{l=1}^{L}\left[p\left(\gamma_{l}\left|y,\tau\right.\right) \right]^{1/t_{l}}p\left(\tau\right)\), то есть вся популяция условна относительно значения \(\tau\)_общего для всех цепей_. Эта стратегия позволяет избежать проблем, описанных ранее, и обеспечивает более быструю сходимость и лучшую смешиваемость между цепями. Описанная процедура имеет дополнительную стоимость - выборка значения \(\tau\). Однако этот шаг является дешевым по сравнению с затратами, необходимыми для выборки \(\gamma_{l}\), \(l=1,\ldots,L\). Существует несколько стратегий, которые могут использоваться для выборки \(\tau\) из (11). Мы нашли полезным применение идеи адаптивного Метрополиса-Гиббса, описанной в работе Робертса и Розенталя (2008). Условия асимптотической сходимости и эргодичности гарантируются, поскольку мы применяем _условие затухающей адаптивности_, то есть ядро перехода стабилизируется при увеличении числа итераций, и _условие ограниченной сходимости_, то есть время сходимости ядра ограничено с вероятностью. В нашей настройке использование адаптивного предложения для выборки \(\tau\) имеет несколько преимуществ, в том числе избегает известных проблем, с которыми сталкивается гиббсовский сэмплер, когда априорное распределение правильное, но относительно плоское (Натараянан и МакКаллох, 1998), как это может происходить для априорных Z-S, когда \(n\) большое, или для независимого случая, рассмотренного Бэ и Маллик (2004). Более того, при ограниченном числе итераций адаптация гарантирует лучшее изучение хвостов \(p\left(\tau\left|y\right.\right)\) по сравнению с фиксированным предложением. Детали реализации и обсуждение условий сходимости см. в Приложении A.2. ### ESS алгоритм В следующем мы обращаемся к нашему предложенному алгоритму, эволюционному стохастическому поиску, называемому ESS. Если выбраны \(g\)-априори, алгоритм обозначается как ESS\(g\), а если выбраны независимые априори, используется обозначение ESS\(i\) (такое же обозначение используется, когда \(\tau\) фиксирован или имеет априорное распределение). Без потери общности мы считаем, что вектор отклика и матрица плана центрированы, а в случае независимых априори матрица плана также масштабирована. Основываясь на двух полных условных распределениях (10) и (11) и ранее введенных локальных и глобальных перемещениях, наш алгоритм ESS может быть кратко описан следующим образом. •Для заданного \(\tau\) выберите состояния популяции \(\bm{\gamma}\) из двух шагов: 1. (i) С вероятностью \(0.5\) выполните локальное перемещение и с вероятностью \(0.5\) примените случайный один из четырех операторов смешивания: \(1\)-точечный, равномерный, блочный и адаптивный оператор смешивания. Если выбрано локальное перемещение, используйте схему сэмплирования FSMH независимо для каждой цепочки (см. приложение A.1). Кроме того, каждые 100 циклов выполните на первой цепочке полное сканирование при помощи сэмплера Гиббса. 2. (ii) Выполните оператор обмена с отложенным отклонением или оператор обмена "все-все" с равной вероятностью. Во время прогрева выбирайте только оператор обмена с отложенным отклонением. •Когда \(\tau\) не является фиксированным, но имеет априорное распределение \(p\left(\tau\right)\), при заданной скрытой бинарной конфигурации \(\bm{\gamma}=\left(\gamma_{1},\ldots,\gamma_{L}\right)\) выберите \(\tau\) с помощью адаптивного сэмплирования Метрополиса-среди-Гиббса (раздел 3.2). С вычислительной точки зрения, мы использовали ту же быструю форму обновления \(S\left(\gamma\right)\), что и Brown _et al._ (1998), основанную на QR-разложении. Помимо численных преимуществ, QR-разложение может работать с случаем \(p_{\gamma}\geq n\). Это позволяет избежать ограничения поиска на модели с \(p_{\gamma}<n\) и помогает смешиванию во время фазы сгорания. ## 4 Производительность ESS ### Примеры реальных данных Первый реальный пример данных - это применение линейной регрессии для исследования генетической регуляции. Чтобы выявить генетические причины вариации в экспрессии (транскрипционной) генов, данные экспрессии генов рассматриваются как количественный фенотип, в то время как генотипные данные (SNP) используются в качестве предикторов, тип анализа, известный как эмоциональный квантильный локус (eQTL). Здесь мы сосредоточимся на способности ESS найти экономичный набор предикторов в наборе данных об животных (Hubner _et al._, 2005), где количество наблюдений, \(n=29\), мало по сравнению с количеством ковариантов \(p=1,421\). Эта ситуация, где \(n\ll p\), довольно распространена в экспериментах с животными, так как контролируются как окружающие источники вариации, так и биологическое разнообразие выборки. Для иллюстрации мы рассматриваем анализ ответа генного выражения, в котором применяется ESS\(g\) с и без гипераприорного распределения на \(\tau\), см. Таблица 1– eQTL. В первом случае благодаря адаптивному предложению марковской цепи для \(\tau\) очень хорошо смешивается, достигая общей доли принятых значений, близкой к целевому значению \(0.44\). Проблем с сходимостью нет, так как трасса стандартного отклонения предложения быстро стабилизируется и хорошо находится внутри границ, см. Рисунок 3. В обоих случаях достигается хорошее смешение между L = 4 цепями (рисунок 1, верхние панели, ESS g с tau = 29). Хотя в случае, изображенном на рисунке 1 с фиксированным tau, сходимость достигается в пространстве произведения [p(гамма_l|y)]^(1/t_l) по визуальному осмотру видно, что каждая цепь _отдельно_ достигает _равновесия_ относительно других; более того, благодаря автоматической настройке размещения температуры во время прогрева, распределения логарифмических апостериорных вероятностей цепей хорошо перекрываются, что обеспечивает эффективный обмен информацией между цепями. Таблица 1-eQTL подтверждает, что автоматический выбор температуры работает хорошо (с и без гиперпараметра tau), достигая коэффициента принятия для отслеживаемого оператора обмена (оператор отложенного отклонения), близкого к выбранной целевой величине 0,50. Оператор всех обменов имеет более высокий коэффициент принятия, в то время как, в отличие от Jasra et al. (2007), общий коэффициент принятия скрещивания разумно высокий: по нашему опыту хорошая производительность оператора скрещивания связана как с оператором отбора (раздел 3.1), так и с новым блочным скрещиванием, которое показывает коэффициент принятия значительно выше, чем у других. Наконец, вычислительное время на том же настольном компьютере (см. подробности в Приложении B.3) достаточно схоже с или без гиперприора tau, соответственно 28 и 30 минут для 25,000 итераций с 5,000 прогрева. Основное различие между двумя реализациями ESS\(g\) связано с размером апостериорной модели: когда \(\tau\) фиксировано на значении \(\tau=29\) (Unit Information Prior, Fernández _et al._, 2001), имеется больше неопределенности и поддержки для больших моделей, см. Рисунок 2 (а). В обоих случаях мы фиксируем \(E\left(p_{\gamma}\right)=4\) и \(V\left(p_{\gamma}\right)=2\), следуя предварительным биологическим знаниям о генетической регуляции. Постериорное среднее коэффициента отбора переменных немного меньше, чем в модели Unit Information Prior, при использовании ESS\(g\) с Z-S prior отдается предпочтение меньшим моделям по сравнению с \(\tau=29\). Лучшая модель, посещенная (и соответствующий \(R_{\gamma}^{2}=1-S(\gamma)/y^{T}y\)), одинакова для обеих версий ESS\(g\), тогда как, при использовании гиперприора на \(\tau\), "индекс стабильности", который показывает, насколько алгоритм упорно остается на первой тысяче (не уникальных) моделей, посещенных по возрастанию апостериорной вероятности (Приложение B.3), показывает большую стабильность, см. Таблица 1 - eQTL. В этом случае наличие данных о уровне сжатия, полученных из данных, помогает алгоритму поиска лучше различать конкурирующие модели. Наш второй пример связан с применением модели (1) в другом геномном примере: \(10,000\) SNPs, отобранных по всему геному в ходе исследования кандидат-гена, используются для прогнозирования изменений метаболических данных масс-спектрометрии в небольшой популяции людей, пример так называемого эксперимента mQTL. Подходящее сокращение размерности данных выполняется для разделения спектров на области или интервалы, и применяется \(\log_{10}\)-преобразование для нормализации сигнала. Мы представляем ключевые результаты, связанные с определенным метаболитным блоком, однако те же комментарии можно распространить на анализ всего набора данных, где мы регрессируем каждый блок метаболитов на генотипные данные (\(n=50\) и \(p=10,000\)). В этом очень сложном случае мы все равно обнаружили эффективное смешение цепей (см. Таблицу 1-mQTL). Обратите внимание, что в этом случае апостериорное среднее \(\tau\), \(63.577\), немного больше, чем априорная информация единичного блока, \(\tau=n\), хотя влияние гипер-априорного значения менее важно, чем в предыдущем примере реальных данных, см. Рисунок 2 (b). В обоих примерах апостериорный размер модели ясно поддерживает полигенный контроль с значительной поддержкой для до четырех генетических точек контроля (Рисунок 2), подчеркивая преимущества выполнения многомерного анализа в геномике по сравнению с традиционным одномерным анализом. Как и ожидалось из-за очень большого количества предикторов, вычислительное время в примере mQTL довольно велико, около 5 часов для 20 000 итераций после начальной фазы (burn-in) из 5 000 итераций, но как показано в Таблице 1 по "индексу стабильности" (≈ 0), мы считаем, что выбранное количество итераций превышает то, что необходимо для достоверного посещения пространства моделей. Для таких крупных задач анализа данных параллелизация кода может значительно сократить время работы на компьютере и идеально подходит для нашего подхода с несколькими цепями. [Таблица 1 см. ниже – Рисунок 1 см. ниже – Рисунок 2 см. ниже – Рисунок 3 см. ниже] Мы также оцениваем превосходство нашего алгоритма ESS, в частности схемы FSMH и блочного скрещивания, по сравнению с более традиционными реализациями EMC, иллюстрируемыми, например, в работе Лианга и Вонга (2000). Хотя мы считаем, что использование широкого портфеля различных ходов позволяет любому алгоритму поиска лучше исследовать сложные пространства моделей, мы повторно проанализировали первый пример реальных данных - анализ eQTL, сравнивая: (i) ESS\(g\) только с FSMH в качестве локального хода _vs_ ESS только с MC\({}^{3}\) в качестве локального хода; (ii) ESS\(g\) только с блочным скрещиванием _vs_ ESS\(g\) только с одноточечным, только с равномерным и только с адаптивным скрещиванием соответственно. Чтобы избежать зависимости результатов от начальной инициализации алгоритма, мы повторили анализ \(25\) раз. Кроме того, для сравнения по справедливости, в эксперименте (i) мы запускали две версии ESS\(g\) для разного числа итераций (\(25,000\) и \(350,000\) соответственно, с выбрасыванием первых \(5,000\) и \(70,000\) соответственно), но с одинаковым числом оцениваемых моделей. Результаты представлены в Таблице 2. Здесь мы сообщаем основные результаты исследования: 1. (i) В течение 25 запусков, ESS g с FSMH достигает одной и той же топовой посещаемой модели 68% (17/25), в то время как ESS g с MC3 достигает одной и той же топовой модели только 28%, с фиксированным τ, и соответственно 88% и 40% с Z-S априорным распределением. Эта способность распространяется на топовые модели, ранжированные по апостериорной вероятности, что дает косвенное доказательство того, что предложенный новый шаг помогает алгоритму увеличить его предсказательную силу. Великое преимущество при использовании схемы FSMH может быть объяснено сравнением подграфика (a) и (c) на Рисунке 1: обмен информацией между цепями для ESS g с MC3 в качестве локального шага при \(p>n\) (и \(p\gg p_{\gamma}\)) является довольно слабым, что отрицает цель EMC. ESS g с MC3 имеет больше трудностей с достижением сходимости в пространстве произведений и, в отличие от ESS g с FSMH, удерживаемая цепочка не так легко покидает локальные моды. Эту последнюю точку можно увидеть, рассмотрев Рисунок 1 (d), который увеличивает правый хвост ядерной плотности \(\log p\left(\gamma\left|y\right.\right)\) для записанной цепочки, объединяя 25 запусков: интересно, что ESS g с FSMH менее "горбатый", что показывает лучшую способность выходить из локальных мод и более эффективно исследовать правый хвост. 2. (ii) Что касается второго сравнения при фиксированном τ, ESS g с только блочным скрещиванием постоянно превосходит другие операторы скрещивания, соответственно 80% против примерно 60% посещаемых лучших моделей (Таблица 2) и моделей с более высокой апостериорной вероятностью (данные не показаны), имеет более высокий уровень принятия (Таблица 3), также показывает большую способность накопления апостериорной массы, как показано на Рисунке 4. Конкретное преимущество блочного скрещивания менее выражено при наличии априорного распределения на τ, но мы уже заметили, что в этом случае наличие гипераприорного распределения на τ значительно улучшает эффективность поиска. [Таблица 2 здесь - Таблица 3 здесь - Рисунок 4 здесь] ### Исследование моделирования Мы кратко сообщаем о всестороннем исследовании производительности ESS в различных симулированных примерах, а также сравнении с SSS. Чтобы сравнение с SSS было справедливым, мы используем ESS\({i}\), версию нашего алгоритма, которая предполагает независимые априорные распределения, \(\Sigma_{\gamma}=\tau I_{p_{\gamma}}\), где \(\tau\) фиксировано равным \(1\). Подробности симулированных примеров (6 настроек) и способ проведения эксперимента на симуляции (25 повторений для каждой настройки) приведены в Приложении B. Основная идея при создании примеров заключалась в том, чтобы провести тестирование нашего алгоритма как в случае \(n>p\), так и в случае \(p>n\), использовать сложные корреляционные структуры, которые ранее использовались в сравнениях G&McC (1993, 1997) и N&G (2004), а также реалистичную корреляционную структуру, полученную из генетических данных, и включить элементы модельной неопределенности в некоторых примерах, используя различные значения регрессионных коэффициентов. В нашем примере мы наблюдали эффективный обмен информацией между цепями (см. Таблицу 4), что показывает хорошие общие проценты принятия движений, которые мы реализовали. Размер проблемы, кажется, не влияет на проценты принятия в Таблице 4, особенно учитывая, что значения \(p\) варьируются от 60 до 1000 между примерами. Мы также исследовали специально производительность глобальных движений (Таблица 5), чтобы проверить настройку температуры и подтвердили хорошую производительность ESS\(i\) с хорошим количеством обменов (не сильно отличающимся от случая, когда соседние цепи выбираются для обмена случайно с равной вероятностью) и хорошими показателями перекрытия между цепями. Во всех примерах были запущены параллельно с использованием ESS\({i}\) и SSS 2.0 (Hans _et al._, 2007) на одном и том же количестве итераций (22 000) и совпадающих гиперпараметрах для размера модели. Сравнение было проведено с учетом предельной вероятности включения, а также возможности достижения моделей с высокой апостериорной вероятностью и способности сохраняться в этой области. Подробное обсуждение всех сравнений можно найти в Приложении B.3. В целом, описательные переменные с ненулевыми эффектами имеют высокую апостериорную вероятность включения для ESS\(i\) во всех примерах, см. Рисунок 6. В целом, два алгоритма согласуются, с дополнительными доказательствами в некоторых примерах (Рисунок 6 (c) и (d)), что ESS\(i\) способен более полно исследовать пространство моделей и, в частности, находить небольшие эффекты, что приводит к размеру апостериорной модели, близкому к истинному. Показатели качества подгонки и стабильности, Таблица 6, хорошо согласуются между ESS\(i\) и SSS. Сравнение показывает, что ключевая особенность SSS - его способность быстро перемещаться к правильной модели и упорствовать в этом - сопровождается недостатком в трудности исследования отдаленных моделей с конкурирующей объяснительной силой, в отличие от ESS\(i\) (загрязненный примерный набор). В целом, ESS\(i\) показывает небольшое улучшение \(R_{\gamma}^{2}\), связанное с его способностью уловить некоторые из небольших эффектов, которые упускает SSS. Наконец, ESS\(i\) проявляет замечательное превосходство в плане вычислительного времени, особенно когда моделируемый (и оцениваемый) \(p_{\gamma}\) велик. В целом, наши сравнения показывают, что мы разработали полностью байесовский сэмплер MCMC-EMC, конкурентоспособный с эффективным поиском, предоставляемым SSS\(i\). В том же духе, что и анализ реального примера данных, мы также оцениваем превосходство схемы FSMH по сравнению с более традиционными реализациями EMC, то есть когда выбирается локальное перемещение MC\({}^{3}\). В то время как обе версии алгоритма поиска посещают практически одни и те же лучшие модели по апостериорной вероятности, ESS уделяет больше внимания лучшим моделям. [Таблица 4 здесь - Таблица 5 здесь - Таблица 6 здесь Фигура 5 здесь - Фигура 6 здесь] ## 5 Обсуждение Основная идея при построении эффективного сэмплера MCMC для \(\gamma\) и \(\tau\) заключается в добавлении дополнительного параметра - температуры, который ослабляет вклад правдоподобия и позволяет избегать локальных максимумов. Однако, параллельное выполнение цепей с разной температурой является дорогостоящим и дополнительные вычислительные затраты должны быть сбалансированы с выгодами, возникающими от "обменов" между цепями. Поэтому мы сосредоточились на разработке хорошей стратегии выбора пар цепей, используя как маргинальную, так и совместную информацию между цепями, пытаясь проводить смелые и более консервативные обмены. Совмещение этого с автоматическим выбором лестницы температур во время прогрева является одним из ключевых элементов нашего алгоритма ESS. Использование PT таким образом может быть эффективным в широком диапазоне ситуаций, где пространство апостериорного распределения является мультимодальным. Для решения случая, когда \(p\) значительно больше чем \(p_{\gamma}\), вторым важным элементом нашего алгоритма является использование шага, похожего на метрополизированную схему Гиббса, который выполняется на подмножестве индексов при локальном обновлении скрытого бинарного вектора, а не при обновлении в соответствии с MC\({}^{3}\) или RJ-подобным подходом. Новый быстрый сканирующий семплер Метрополиса-Гастингса, который мы предлагаем для выполнения этих локальных перемещений, достигает эффективного компромисса между полной схемой Гиббса, которая не всегда выполнима при больших \(p\), и простыми добавлением/удалением перемещений. Сравнение FSMH _vs_ схемы MC\({}^{3}\) на примере реальных данных и в симуляционном исследовании показывает превосходство нашего нового локального перемещения. Когда модель с априорным распределением на коэффициенте выбора переменных \(\tau\) предпочитается, обновление самого \(\tau\) не представляет особых трудностей и вычислительно недорого. Более того, использование адаптивного сэмплера делает алгоритм самодостаточным, без необходимости настройки предлагаемой дисперсии вручную. Эта последняя стратегия работает отлично как в случае \(g\)-предпочтения, так и в случае независимого априорного распределения, как показано в разделах 4.1 и 4.2. В нашей текущей реализации не используется вывод нагретых цепей для статистического вывода. Вопрос о возможности сокращения дисперсии в духе Gramacy _et al._ (2007) является предметом дальнейшего исследования, выходящего за рамки данной работы. На данный момент наш подход был применен только к линейной регрессии с одномерным откликом \(y\). Интересное обобщение заключается в многомерном \(n\times q\) отклике \(Y\) и определении регрессоров, которые совместно предсказывают \(Y\) (Brown _et al._, 1998). Большая часть нашей установки и алгоритма легко применима и мы уже реализовали наш алгоритм в этой рамке в сложном исследовании в геномике с многомерными результатами. ## Благодарности Авторы благодарны Норберту Хюбнеру и Тимоти Айтману за предоставление данных примера eQTL, Гарету Робертсу и Джеффри Розенталю за полезные обсуждения адаптации и Михаилу Папатомасу за подробные комментарии. Сильвия Ричардсон признает поддержку гранта MRC GO.600609. ## Приложение А Технические детали реализации EMC В этом разделе мы описываем некоторые технические детали, опущенные в статье и связанные с схемами выборки, которые мы использовали для выборки популяции бинарных латентных векторов \(\bm{\gamma}\) и коэффициента отбора \(\tau\). ### EMC сэмплер для \(\bm{\gamma}\) #### Локальное перемещение: схема FSMH Пусть \(\gamma_{l,j}\), где \(l=1,\ldots,L\) и \(j=1,\ldots,p\), обозначает \(j\)-й скрытый бинарный индикатор в \(l\)-й цепи. Как и в работе Kohn _et al._ (2001), пусть \(\gamma_{l,j}^{\left(1\right)}=\left(\gamma_{l,1},\ldots,\gamma_{l,j-1},\gamma_ {l,j}=1,\gamma_{l,j+1},\ldots,\gamma_{l,p}\right)^{T}\) и \(\gamma_{l,j}^{\left(0\right)}=\left(\gamma_{l,1},\ldots,\gamma_{l,j-1},\gamma_ {l,j}=0,\gamma_{l,j+1},\ldots,\gamma_{l,p}\right)^{T}\). Кроме того, пусть \(L_{l,j}^{\left(1\right)}\propto p\left(y\left|\gamma_{l,j}^{\left(1\right)}, \tau\right.\right)\) и \(L_{l,j}^{\left(0\right)}\propto p\left(y\left|\gamma_{l,j}^{\left(0\right)}, \tau\right.\right)\) и, наконец, \(\theta_{l,j}^{\left(1\right)}=p\left(\gamma_{l,j}=1\left|\gamma_{l,j^{-}} \right.\right)\) и \(\theta_{l,j}^{\left(0\right)}=1-\theta_{l,j}^{\left(1\right)}\). Из (6) легко доказать, что \[\theta_{l,j}^{\left(1\right)}=p\left(\gamma_{l,j}=1\left|\gamma_{l,j^{-}} \right.\right)=\frac{p_{\gamma_{l}}+a_{\omega}-1}{p+a_{\omega}+b_{\omega}-1},\] (A.1) где \(p_{\gamma_{l}}\) обозначает текущий размер модели для \(l\)-ой цепи. Используя приведенное уравнение, для \(\gamma_{l,j}=1\) нормализованная версия (12) может быть записана следующим образом: \[\left[p(\gamma_{l,j}=1|y,\gamma_{l,j^{-}},\tau)\right]^{1/t_{l}}=\frac{\left(\theta_{l,j}^{(1)}\right)^{1/t_{l}}\left(L_{l,j}^{(1)}\right)^{1/t_{l}}}{S(1/t_{l})},\] (A.2) где \(S\left(1/t_{l}\right)=\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}} \left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}+\left.\theta_{l,j}^{\left(0 \right)}\right.^{1/t_{l}}\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\) с \(\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}\) определен аналогично. Следовательно, если \(\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\) очень маленькое, то \(\left[p\left(\gamma_{l,j}=1\left|y,\gamma_{l,j^{-}},\tau\right.\right)\right]^ {1/t_{l}}\) тоже маленькое. Таким образом, для сэмплера Гиббса с бета-биномиальным априорным распределением на пространстве моделей, апостериорная вероятность \(\gamma_{l,j}=1\) критически зависит от \(\left.\theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\). Следующее мы получаем схему Fast Scan Metropolis-Hastings, специализированную для Evolutionary Monte Carlo или параллельного темперинга. Мы определяем \(Q\left(1\to 0\right)=Q\left(\gamma_{l,j}^{\left(1\right)}\to \gamma_{l,j}^{\left(0\right)}\right)\) как вероятность предложения перехода из \(1\) в \(0\) и \(Q\left(0\to 1\right)\) как вероятность предложения перехода из \(0\) в \(1\) для \(j\)-той переменной и \(l\)-той цепи. Кроме того, используя введенную ранее нотацию, Метрополис-в-Гиббсовом варианте (12) для перехода из \(0\) в \(1\) в локальном шаге EMC будет. \[\alpha_{l}^{\text{MwG}}\left(0\to 1\right)=\min\left\{1,\frac{\left. \theta_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left.L_{l,j}^{\left(1\right)} \right.^{1/t_{l}}}{\left.\theta_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left.L _{l,j}^{\left(0\right)}\right.^{1/t_{l}}}\frac{Q\left(1\to 0\right)}{Q \left(0\to 1\right)}\right\}\] (А.3) соответствующим выражением для \(\alpha_{l}^{\text{MwG}}\left(1\to 0\right)\). Доказательства предложений опущены, так как их легко проверить. Сначала мы представляем следующее предложение, которое полезно для расчета вероятности принятия в схеме FSMH. **Предложение 1**: Следующие три условия эквивалентны: a) \(\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left.\left/L_{l,j}^{\left(1 \right)}\right.^{1/t_{l}}\geq 1\right.\); b) \(\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left/\tilde{S}\left(1/t_{l} \right)\geq 1\right.\); c)\(\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left/\tilde{S}\left(1/t_{l} \right)<1\right.\), где \(\tilde{S}\left(1/t_{l}\right)=S\left(1/t_{l}\right)\left/\left(\left.\theta_{l ,j}^{\left(1\right)}\right.^{1/t_{l}}+\left.\theta_{l,j}^{\left(0\right)} \right.^{1/t_{l}}\right)\right.\) является выпуклой комбинацией предельной вероятности \(\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\) и \(\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\) с весами \(\tilde{\theta}_{l,j}^{\left(1\right)}\left(1/t_{l}\right)=\left.\theta_{l,j}^{ \left(1\right)}\right.^{1/t_{l}}\left/\left(\left.\theta_{l,j}^{\left(1\right) }\right.^{1/t_{l}}+\left.\theta_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\right)\right.\) и \(\tilde{\theta}_{l,j}^{\left(0\right)}\left(1/t_{l}\right)=1-\tilde{\theta}_{l, j}^{\left(1\right)}\left(1/t_{l}\right)\). \({}_{\blacksquare}\) Схема FSMH можно рассматривать как случайный сканирующий алгоритм Метрополиса-внутри-Гиббса, где количество оценок связано с предыдущим/текущим размером модели и температурой, присоединенной к цепи. Требования к вычислительной мощности для дополнительного шага принятия/отклонения очень незначительны, поскольку используется нормализованная температурная версия (A.1). **Утверждение 2**: Пусть \(l=1,\ldots,L\), \(j=1,\ldots,p\) (или любая их перестановка), \(Q^{\text{FSMH}}\left(0\to 1\right)=\tilde{\theta}_{l,j}^{\left(1\right )}\left(1/t_{l}\right)\) и \(Q^{\text{FSMH}}\left(1\to 0\right)=\tilde{\theta}_{l,j}^{\left(0\right )}\left(1/t_{l}\right)\) с условием \(\tilde{\theta}_{l,j}^{\left(0\right)}\left(1/t_{l}\right)=1-\tilde{\theta}_{l, j}^{\left(1\right)}\left(1/t_{l}\right)\). Вероятности принятия равны \[\alpha_{l}^{\text{FSMH}}\left(0\to 1\right)=\left\{\begin{tabular}[]{ ll}$1$&$\text{если }\left. L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left/\left.L _{l,j}^{\left(0\right)}\right.^{1/t_{l}}\right.\geq 1$\\ $\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(0 \right)}\right.^{1/t_{l}}\right.$&$\text{если }\left.L_{l,j}^{\left(1\right)} \right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\right.< 1$\end{tabular}\right.\] (A.4) \[\alpha_{l}^{\text{FSMH}}\left(1\to 0\right)=\left\{\begin{tabular}[]{ ll}$1$&$\text{если }\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left/\left.L _{l,j}^{\left(1\right)}\right.^{1/t_{l}}\right.\geq 1$\\ $\left.L_{l,j}^{\left(0\right)}\right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(1 \right)}\right.^{1/t_{l}}\right.$&$\text{если }\left.L_{l,j}^{\left(0\right)} \right.^{1/t_{l}}\left/\left.L_{l,j}^{\left(1\right)}\right.^{1/t_{l}}<1\right .$\end{tabular}\right.\] (A.5) \({}_{\blacksquare}\) Вышеуказанная схема выборки работает следующим образом. Для заданной \(l\)-й цепи, если \(\gamma_{lj}=0\) (и аналогично для \(\gamma_{lj}=1\)), она предлагает новое значение из бернуллиевского распределения с вероятностью \(\tilde{\theta}_{l,j}^{\left(1\right)}\left(1/t_{l}\right)\): если предлагаемое значение отличается от текущего, оно оценивает (A.4) (и аналогично A.5), в противном случае выбирается новая ко-вариация. Наконец, можно доказать, что сэмплер Гиббса эффективнее, чем схема FSMH, то есть при фиксированном числе итераций, стандартная ошибка сэмплирования МСМС Гиббса ниже, чем для сэмплера FSMH. Однако, сэмплер Гиббса требует больше вычислительных ресурсов, поэтому, если \(p\) очень велико, как описано в Kohn _et al._ (2001), схема FSMH становится более эффективной в сравнении с операцией с плавающей запятой. #### Глобальное перемещение: оператор обмена Оператор обмена можно рассматривать как чрезвычайный случай оператора скрещивания, где первая предложенная цепь получает полное состояние второй цепи \(\gamma_{l}^{\prime}=\gamma_{r}\), а вторая предложенная цепь получает полное состояние первой цепи \(\gamma_{r}^{\prime}=\gamma_{l}\), соответственно. Для достижения высокого уровня принятия, оператор обмена обычно применяется к смежным цепям в температурной лестнице, что ограничивает его способность к смешиванию. Чтобы достичь лучшего смешивания, мы реализовали два различных подхода: первый основан на работе Ясра и др. (2007) и связанной идеи отложенного отклонения (Грин и Мира, 2001); второй - на распределении Гиббса на пары всех возможных цепей (Кальво, 2005). 1. Оператор задержки отклонения обмена сначала пытается поменять состояние цепей, которые обычно находятся далеко друг от друга по температурной лестнице, но, если предложенное перемещение было отклонено, он выполняет более традиционный (равномерный) выбор соседних пар, увеличивая общую смешиваемость между цепями, с одной стороны, без резкого снижения коэффициента принятия с другой стороны. Однако его гибкость требует дополнительных вычислительных затрат и, в частности, дополнительной оценки псевдо-перемещения, необходимого для поддержания детального баланса (Грин и Мира, 2001). Подробности приведены ниже. Предположим, что две цепи \(l\) и \(r\) выбираются случайным образом, \(l\neq r\), для обмена их двоичными скрытыми векторами. Тогда, при условии, что \(\gamma_{l}^{\prime}=\gamma_{r}\), \(\gamma_{r}^{\prime}=\gamma_{l}\) и \(Q_{t}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\right)=Q_{t}\left(\bm{ \gamma}^{\prime}\rightarrow\bm{\gamma}\right)\), (13) принимает вид \[\alpha_{1}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime}\right)=\min\left\{1 ,\frac{\exp\left\{f\left(\gamma_{r}\left|\tau\right.\right)/t_{l}+f\left( \gamma_{l}\left|\tau\right.\right)/t_{r}\right\}}{\exp\left\{f\left(\gamma_{l} \left|\tau\right.\right)/t_{l}+f\left(\gamma_{r}\left|\tau\right.\right)/t_{r} \right\}}\right\}.\] Поскольку две цепи выбираются случайно, вышеупомянутая вероятность принятия экспоненциально уменьшается с разностью \(\left|1/t_{l}-1/t_{r}\right|\) и, следовательно, большинство предложенных перемещений отклоняются. Если они отклонены, между двумя случайными соседними цепями применяется отложенное перемещение типа отклонения, при этом \(l\) - первая, а \(s\), \(\left|l-s\right|=1\) - вторая, возникает новая вероятность принятия \[\alpha_{2}\left(\bm{\gamma}\rightarrow\bm{\gamma}^{\prime\prime}\right)=\min \left\{1,\frac{\exp\left\{f\left(\gamma_{s}\left|\tau\right.\right)/t_{l}+f \left(\gamma_{l}\left|\tau\right.\right)/t_{s}\right\}}{\exp\left\{f\left( \gamma_{l}\left|\tau\right.\right)/t_{l}+f\left(\gamma_{s}\left|\tau\right. \right)/t_{s}\right\}}\frac{1-\alpha_{1}\left(\bm{\gamma}^{\prime\prime} \rightarrow\bm{\gamma}^{\ast}\right)}{1-\alpha_{1}\left(\bm{\gamma}\to \bm{\gamma}^{\prime}\right)}\right\},\] где псевдо-перемещение \(\bm{\gamma}^{\ast}\) необходимо для поддержания условия детального баланса (Грин и Мира, 2001). 2. В качестве альтернативы, мы предпринимаем более смелый оператор "все-обмен". Обмен состояниями двух цепей, находящихся далеко друг от друга по температурной лестнице, ускоряет сходимость симуляции, так как он заменяет несколько соседних обменов одним перемещением. Однако это перемещение может быть рассмотрено как редкое событие, вероятность принятия которого низка и неизвестна. Поскольку полный набор возможных обменов является конечным и дискретным, легко и вычислительно недорого рассчитать все \(L\left(L-1\right)/2\) коэффициенты принятия обмена между парами цепей, включая редкие, \(\tilde{p}_{l,r}=\exp\left\{\left(f\left(\gamma_{r}\left|\tau\right.\right)-f \left(\gamma_{l}\left|\tau\right.\right)\right)\left(1/t_{l}-1/t_{r}\right)\right\}\). Для поддержания условия детального баланса, возможность не выполнять никакой обмен (отклонение) должна быть добавлена с ненормализованной вероятностью один. Наконец, цепи, состояния которых меняются местами, выбираются случайно с вероятностью, равной \[p_{h}=\frac{\tilde{p}_{h}}{\sum_{h=1}^{1+L\left(L-1\right)/2}\tilde{p}_{h}},\] (A.6) где в (A.6) каждая пара \(\left(l,r<l\right)\) обозначается одним числом \(h\), \(\tilde{p}_{h}=\tilde{p}_{l,r}\), включая отклонение, \(h=1\). #### Размещение температуры Сначала выбирается число \( L \) цепей, близкое к сложности проблемы, то есть \( E\left(p_{\gamma}\right) \), хотя при этом нужно учитывать размер данных и вычислительные ограничения. Во-вторых, мы устанавливаем первую температурную шкалу на геометрической основе так, чтобы \( t_{l+1}/t_{l}=b \), \( b>1 \), \( l=1,\ldots,L \) с относительно большим значением \( b \), например, \( b=4 \). Наконец, мы применяем стратегию, аналогичную описанной в работе Робертса и Розентоля (2008), но _ограниченной байесовским предварительным запуском_, при этом отслеживается только коэффициент принятия оператора задержанного отклонения обмена. После \( k \)-ой "партии" прогонов моделирования Монте-Карло, которые выбираются, но обычно устанавливаются равными \( 100 \), мы обновляем \( b_{k} \), значение постоянной \( b \) до \( k \)-ой партии, путем добавления или вычитания количества \( \delta_{b} \), чтобы коэффициент принятия оператора задержанного отклонения обмена был как можно ближе к \( 0.50 \) (Лиу, 2001; Жасра _и др._, 2007), \( b_{k+1}=2^{\log_{2}b_{k}\pm\delta_{b}} \). Уточненно, значение \( \delta_{b} \) выбирается таким образом, чтобы в конце предварительного запуска значение \( b \) могло быть равным 1. Точнее, мы устанавливаем значение \( \delta_{b} \) как \( \log_{2}\left(b_{1}\right)/\tilde{K} \), где \( b_{1} \) - это первое значение, присвоенное геометрическому коэффициенту, а \( \tilde{K} \) - общее количество партий в предварительном запуске. ### Адаптивный Метрополис-внутри-Гиббса для \(\tau\) #### Аппроксимация Лапласа для условного маргинального правдоподобия При модели (1) и априорной спецификации для \(\alpha\), (2) и (3), мы предоставляем лапласовскую аппроксимацию для \(p\left(y\left|\gamma,\tau\right.\right)\) в случае \(g\)-предпочтительности, в то время как для независимого случая аппроксимацию можно получить, следуя тому же логическому подходу. Для удобства обозначений мы опускаем индекс последовательности и предполагаем, что наблюдаемые ответы \(y\) были центрированы с нулевым средним значением, т. е. \(\left(y-\bar{y}_{n}\right)\equiv y\). В дальнейшем мы будем различать случаи, когда мода апостериорной оценки \(\hat{\tau}_{\gamma}\) является решением кубического или квадратичного уравнения. Условия существования решений, а также те, которые гарантируют положительно полуопределенность аппроксимации дисперсии, также приводятся в памяти. \[p\left(y\left|\gamma\right.\right) = \int\exp\left\{\log\left(p\left(y\left|\gamma,\tau\right.\right)p \left(\tau\right)\right)\right\}d\tau\] \[\approx \sqrt{2\pi}\sigma_{\hat{\lambda}}\left(\log p\left(y\left|\gamma, \hat{\lambda}\right.\right)+\log p\left(\hat{\lambda}\right)+\log J\left(\hat{ \lambda}\right)\right),\] где \(\hat{\lambda}\) - постериорный мод после преобразования \(\lambda=\log\left(\tau\right)\), которое необходимо для избежания проблем на границе, \(\sigma_{\hat{\lambda}}\) - приближенный квадратный корень из дисперсии, рассчитанный в \(\hat{\lambda}\), а \(J\left(\cdot\right)\) - якобиан преобразования. Подробности о приближении Лапласа можно найти в работе Тирни и Кадэна (1986). Аналогичные выводы, когда \(p\left(\sigma^{2}\right)\propto\sigma^{-2}\), представлены в работе Лянг _et al._ (2008). Наконец, на протяжении презентации мы будем предполагать, что \(n>p_{\gamma}\) и что \(a_{g}\) и \(b_{g}\) фиксированы маленькие, как в работе Кона _et al._ (2001). Кубическое уравнение для априорных распределений Зеллнера-Сиоу Если \(p\left(\tau\right)=InvGa\left(a_{\tau},b_{\tau}\right)\), то мода апостериорного распределения \(\hat{\lambda}\) является единственным положительным корнем интегранда \[I_{\lambda}=\left(1+e^{\lambda}\right)^{\left(2a_{\sigma}+n-1-p_{\gamma}\right)/2}\left\{2b_{\sigma}\left(1+e^{\lambda}\right)+y^{T}y\left[1+e^{\lambda} \left(1-R_{\gamma}^{2}\right)\right]\right\}^{-\left(2a_{\sigma}+n-1\right)/2} \frac{e^{-b_{\tau}/e^{\lambda}}}{\left(e^{\lambda}\right)^{a_{\tau}+1}}e^{ \lambda},\] где последний множитель в уравнении выше \(e^{\lambda}=\left|de^{\lambda}/d\lambda\right|\) является Якобианом преобразования. После взятия производной от логарифма преобразования и некоторых алгебраических преобразований можно показать, что \(e^{\hat{\lambda}}\) является решением кубического уравнения \[e^{3\lambda}+\frac{c_{1}c_{3}-c_{2}c_{4}-(c_{3}+c_{4})a_{\tau}+c_{4 }b_{\tau}}{(c_{1}-c_{2}-a_{\tau})c_{4}}e^{2\lambda}+\frac{-c_{3}a_{ \tau}+(c_{3}+c_{4})b_{\tau}}{(c_{1}-c_{2}-a_{\tau})c_{4} }e^{\lambda}+\frac{c_{3}b_{\tau}}{(c_{1}-c_{2}-a_{\tau})c_{4}}=0\] (A.7) и это \[\sigma_{\hat{\lambda}}^{2} = \left.-\frac{1}{\left(\log p\left(y\left|\gamma,\lambda\right. \right)+\log p\left(\lambda\right)\right)^{\prime\prime}}\right|_{\lambda=\hat {\lambda}}\] (A.8) \[= \left[-c_{1}\frac{e^{\lambda}}{\left(1+e^{\lambda}\right)^{2}}+c_ {2}\frac{c_{3}c_{4}e^{\lambda}}{\left(c_{3}+c_{4}e^{\lambda}\right)^{2}}+\frac {b_{\tau}}{e^{\lambda}}\right]_{\lambda=\hat{\lambda}}^{-1},\] \[\sigma_{\hat{\lambda}}^{2} = \left.-\frac{1}{\left(\log p\left(y\left|\gamma,\lambda\right. \right)+\log p\left(\lambda\right)\right)^{\prime\prime}}\right|_{\lambda=\hat {\lambda}}\] (A.8) \[= \left[-c_{1}\frac{e^{\lambda}}{\left(1+e^{\lambda}\right)^{2}}+c_ {2}\frac{c_{3}c_{4}e^{\lambda}}{\left(c_{3}+c_{4}e^{\lambda}\right)^{2}}+\frac {b_{\tau}}{e^{\lambda}}\right]_{\lambda=\hat{\lambda}}^{-1},\] где \(c_{1}=\left(2a_{\sigma}+n-1-p_{\gamma}\right)/2\), \(c_{2}=\left(2a_{\sigma}+n-1\right)/2\), \(c_{3}=2b_{\sigma}+y^{T}y\) и \(c_{4}=2b_{\sigma}+y^{T}y\left(1-R_{\gamma}^{2}\right)\). Согласно Liang _et al._ (2008), так как \(\lim_{\lambda\rightarrow-\infty}\partial I_{\lambda}/\partial\lambda>0\), потому что \(c_{3}b_{\tau}>0\), и \(\lim_{\lambda\rightarrow\infty}\partial I_{\lambda}/\partial\lambda<0\), потому что \(\left(c_{1}-c_{2}-a_{\tau}\right)c_{4}<0\), существует как минимум одно действительное положительное решение. Более того, так как \(-\left(c_{3}b_{\tau}\right)/\left(c_{1}-c_{2}-a_{\tau}\right)c_{4}>0\), оставшиеся два действительных решения должны иметь одинаковый знак (Abramowitz and Stegun, 1970). Необходимым условием для существования только одного действительного положительного решения является то, что сумма всех попарных произведений коэффициентов отрицательна. \[\frac{-c_{3}a_{\tau}+\left(c_{3}+c_{4}\right)b_{\tau}}{\left(c_{1}-c_{2}-a_{ \tau}\right)c_{4}}<0\] should be translated to Russian as: \[\frac{-c_{3}a_{\tau}+\left(c_{3}+c_{4}\right)b_{\tau}}{\left(c_{1}-c_{2}-a_{ \tau}\right)c_{4}}<0\] и это происходит, если \(b_{\tau}/a_{\tau}>c_{3}/\left(c_{3}+c_{4}\right)\). Когда \(R_{\gamma}^{2}\to 0\) и, следовательно, \(c_{3}=c_{4}\), вышеуказанное условие соответствует \(b_{\tau}>a_{\tau}/2\), и когда \(R_{\gamma}^{2}\to 1\), поскольку \(c_{3}/\left(c_{3}+c_{4}\right)\approx 1\), особенно когда \(y^{T}y\) велико, что может ожидаться при большом \(n\), условие эквивалентно \(b_{\tau}>a_{\tau}\). Таким образом, оказывается, что достаточным условием для существования только одного действительного положительного решения в (A.1) является \(b_{\tau}>a_{\tau}\). Положительная полуопределенность приближенной дисперсии может быть доказана следующим образом. Прежде всего стоит отметить, что все члены в (A.8) имеют одинаковый порядок \(O_{p}\left(e^{-\lambda}\right)\). Затем, когда \(R_{\gamma}^{2}\to 0\), положительная полуопределенность всегда гарантирована, в то время как при \(R_{\gamma}^{2}\to 1\), при условии, что \(y^{T}y\) большое, средний член в (A.8) стремится к нулю и условие выполняется, если \(b_{\tau}>c_{1}\). Квадратное уравнение для априорного распределения Liang _et al._ (2008) Если \(p(\tau) \propto (1+\tau)^{-c_{\tau}}\), где \(c_{\tau} > 0\), то \(e^{\hat{\lambda}}\) является только положительным корнем подынтегральной функции. \[I_{\lambda}=\left(1+e^{\lambda}\right)^{\left(2a_{\sigma}+n-1-p_{\gamma}-c_{ \tau}\right)/2}\left\{2b_{\sigma}\left(1+e^{\lambda}\right)+y^{T}y\left[1+e^{ \lambda}\left(1-R_{\gamma}^{2}\right)\right]\right\}^{-\left(2a_{\sigma}+n-1 \right)/2}e^{\lambda}\] или, после первой производной логарифма, решение квадратного уравнения \[\left(c_{1}^{\ast}-c_{2}+1\right)c_{4}e^{2\lambda}+\left(c_{1}^{\ast}c_{3}-c_{ 2}c_{4}+c_{3}+c_{4}\right)e^{\lambda}+c_{3}=0\] (A.9) (A.9) means (A.9) значит с \(c_{1}^{\ast}=\left[2a_{\sigma}+n-1-\left(p_{\gamma}+2c_{\tau}\right)\right]/2\) и \(c_{2}\), \(c_{3}\) и \(c_{4}\) определены, как указано выше. Дискриминант квадратного уравнения равен \(\Delta=\left(c_{1}^{\ast}c_{3}-c_{2}c_{4}c_{3}+c_{3}+c_{4}\right)^{2}-4\left(c _{1}^{\ast}-c_{2}+1\right)c_{4}c_{3}\), который всегда больше нуля, и поэтому существуют два действительных корня. Поскольку один из них положителен, чтобы доказать, что (A.9) имеет только одно положительное решение, необходимо показать, что. \[\frac{-\left(c_{1}^{\ast}c_{3}-c_{2}c_{4}+c_{3}+c_{4}\right)-\Delta^{1/2}}{2 \left(c_{1}^{\ast}-c_{2}+1\right)c_{4}}<0\] will be translated as: \[\frac{-\left(c_{1}^{\ast}c_{3}-c_{2}c_{4}+c_{3}+c_{4}\right)-\Delta^{1/2}}{2 \left(c_{1}^{\ast}-c_{2}+1\right)c_{4}}<0\] что верно при условии \(\left(c_{1}^{\ast}-c_{2}+1\right)c_{4}c_{3}<0\). Более того, приближенная дисперсия может быть записана как \[\sigma_{\hat{\lambda}}^{2}=\left[-c_{1}^{\ast}\frac{e^{\lambda}}{\left(1+e^{ \lambda}\right)^{2}}+c_{2}\frac{c_{3}c_{4}e^{\lambda}}{\left(c_{3}+c_{4}e^{ \lambda}\right)^{2}}\right]_{\lambda=\hat{\lambda}}^{-1}\] (A.10) \[\sigma_{\hat{\lambda}}^{2}=\left[-c_{1}^{\ast}\frac{e^{\lambda}}{\left(1+e^{ \lambda}\right)^{2}}+c_{2}\frac{c_{3}c_{4}e^{\lambda}}{\left(c_{3}+c_{4}e^{ \lambda}\right)^{2}}\right]_{\lambda=\hat{\lambda}}^{-1}\] (А.10) который является положительно полуопределенным, когда \(R_{\gamma}^{2}\to 0\) если \(c_{2}>c_{1}^{\ast}\), что всегда выполняется, в то время как, если \(R_{\gamma}^{2}\to 1\) и \(y^{T}y\) велико, уравнение (A.10) не является положительным за исключением случая \(p_{\gamma}+2c_{\tau}>2a_{\sigma}+n-1\). Явное решение моды апостериорного распределения также доступно. \[\hat{\tau}_{\gamma} = \max\left\{\frac{\left(c_{4}-c_{3}\right)/\left(c_{1}^{\ast}-c_{2 }\right)}{c_{4}/c_{1}^{\ast}}-1,0\right\}\] (A.11) \[= \max\left\{\frac{R_{\gamma}^{2}/\left(p_{\gamma}+2c_{\tau}\right) }{\left[2b_{\sigma}/\left(y^{T}y\right)+\left(1-R_{\gamma}^{2}\right)\right]/ \left[2a_{\sigma}+n-1-\left(p_{\gamma}+2c_{\tau}\right)\right]}-1,0\right\}\] что соответствует ММП, если \(c_{\tau}=0\). #### Уменьшение адаптивных и ограниченных условий Поскольку \(\tau\) определено на положительной оси вещественных чисел, мы предлагаем новое значение \(\tau\) в логарифмической шкале. В частности, в качестве предложения мы используем нормальное распределение с центром в текущем значении \(\log\left(\tau\right)\) в случае \(g\)-перитического и независимого априорного распределения. Дисперсия распределения предложений контролируется, как показано в работе Робертса и Розенталя (2008): каждые \(100\) проходов EMC, то же значение проходов, используемых при размещении температуры, мы контролируем коэффициент принятия алгоритма Метрополиса-внутри-Гиббса: если он ниже (выше) оптимального коэффициента принятия, т.е. 0.44, в \(k\)-том пакете проходов EMC добавляется (вычитается) константа \(\delta_{\tau}(k)\) к \(ls_{k}\), логарифмическому стандартному отклонению распределения предложений. Значение константы, добавляемой или вычитаемой, довольно произвольно, но мы нашли полезным установить его как \(\left|ls_{1}-5\right|/\tilde{K}\), где \(\tilde{K}\) - общее количество пакетов в периоде разогрева: во время разогрева логарифмическое стандартное отклонение должно быть способно достичь любых значений в пределах \(\pm 5\) в логарифмической шкале от начального значения \(ls_{1}\), как правило, установленного равным нулю. "Убывающее адаптивное условие" обеспечивается путем наложения ограничения \(\delta_{\tau}\left(k\right)=\min\{\left|ls_{1}-5\right|/\tilde{K},k^{-1/2}\}\), где \(k\) - текущее количество пакетов, включая разогрев. Чтобы обеспечить "ограниченное условие сходимости", мы следуем работе Робертса и Розенталя (2008), ограничивая каждое \(ls_{k}\) значениями из интервала \(\left[M_{1},M_{2}\right]\) и устанавливаем их равными соответственно \(M_{1}=-10\) и \(M_{2}=10\). На практике эти ограничения не создают никаких ограничений, так как последовательность стандартных отклонений распределения предложений практически мгновенно стабилизируется, что указывает на то, что переходное ядро сходится за ограниченное количество пакетов, см. рисунок 2. ## Приложение B: Производительность ESS: Симуляционное исследование В этом разделе мы подробно рассмотрим производительность ESS в нескольких примерах моделирования. Основные выводы будут суммированы в разделе 4.2. Сначала мы анализируем моделированные примеры с ESS\({i}\), версией нашего алгоритма, которая предполагает независимые априорные распределения, \(\Sigma_{\gamma}=\tau I_{p_{\gamma}}\), чтобы можно было сравнить с SSS, который также реализует независимое априорное распределение. Более того, чтобы сравнение с SSS было справедливым, в симуляционном исследовании выполняется только первый шаг алгоритма, описанного в разделе 3.3, с фиксированным значением \(\tau = 1\). Как и в SSS, стандартизация ковариат выполняется перед запуском ESS\({i}\). Мы запускаем ESS\({i}\) и SSS 2.0 (Hans _et al._, 2007) с одинаковым числом итераций (22,000) и с соответствующими гиперпараметрами для размера модели. Во-вторых, чтобы обсудить свойства смешивания ESS, когда задано априорное распределение \(p\left(\tau\right)\) на \(\tau\), мы реализуем как априорное распределение \(g\), так и независимое априорное распределение для конкретного симулированного эксперимента. Чтобы быть точными, в первом случае мы будем использовать априорные распределения Зеллнера-Сиоу (8), а во втором случае мы определим правильное, но размытое экспоненциальное распределение, как рекомендовали Бае и Маллик (2004). ### Моделирование экспериментов Мы применяем ESS с независимыми априорными распределениями к обширному и сложному набору симулированных примеров с \(\tau\) фиксированным на \(1\): первые три примера (Ex1-Ex3) рассматривают случай \(n>p\), в то время как оставшиеся три (Ex4-Ex6) имеют \(p>n\). Кроме того, во всех примерах, кроме последнего, мы симулируем матрицу плана, создавая все более сложные структуры корреляции между ковариатами, чтобы протестировать предложенный алгоритм в различных и становящихся все более реалистичных сценариях. В последнем примере мы используем в качестве матрицы плана генетический регион, охватывающий \(500\)-kb из проекта HapMap (Altshuler _et al._, 2005). Симулированные эксперименты Ex1-Ex5 имеют общую особенность в том, как мы строим \(X\). Для создания умеренной до сильной корреляции мы нашли полезными обращаться к двум симулированным примерам в работе George and McCulloch, G&McC в дальнейшем (1993) и в работе G&McC (1997): во всех случаях мы называем матрицу дизайна \(X_{1}\) (\(n\times 60\)) и \(X_{2}\)\((n\times 15)\), полученные из этих двух примеров. В частности, \(j\)-й столбец \(X_{1}\), обозначенный как \(X_{\left(1\right)j}\), моделируется как \(X_{\left(1\right)j}=X_{j}^{\ast}+Z\), где \(X_{1}^{\ast},\ldots,X_{60}^{\ast}\) iid \(\sim N_{n}\left(0,1\right)\) независимо от \(Z\sim N_{n}\left(0,1\right)\), что приводит к попарной корреляции \(0.5\). \(X_{2}\) генерируется следующим образом: сначала мы симулировали \(Z_{1},\ldots,Z_{15}\) iid \(\sim N_{n}\left(0,1\right)\), и мы устанавливаем \(X_{\left(2\right)j}=Z_{i}+2Z_{j}\) только для \(j=1,3,5,8,9,10,12,13,14,15\). Чтобы создать сильную мультиколлинеарность, мы устанавливаем \(X_{\left(2\right)2}=X_{\left(2\right)1}+0.15Z_{2}\), \(X_{\left(2\right)4}=X_{\left(2\right)3}+0.15Z_{4}\), \(X_{\left(2\right)6}=X_{\left(2\right)5}+0.15Z_{6}\), \(X_{\left(2\right)7}=X_{\left(2\right)8}+X_{\left(2\right)9}-X_{\left(2\right)10}+0.15Z_{7}\) и \(X_{\left(2\right)11}=X_{\left(2\right)14}+X_{\left(2\right)15}-X_{\left(2\right)12}-X_{\left(2\right)13}+0.15Z_{11}\). Вводится попарная корреляция около 0.998 между \(X_{\left(2\right)j}\) и \(X_{\left(2\right)j+1}\) для \(j=1,3,5\), и аналогичная сильная линейная зависимость присутствует внутри множества \(\left(X_{\left(2\right)7},X_{\left(2\right)8},X_{\left(2\right)9},X_{\left(2\right)10}\right)\) и \(\left(X_{\left(2\right)11},X_{\left(2\right)12},X_{\left(2\right)13},X_{\left(2\right)14},X_{\left(2\right)15}\right)\). Затем, как в Nott и Green, N&G в дальнейшем, (2004) Пример 2, более сложные структуры создаются путем размещения рядом комбинаций \(X_{1}\) и/или \(X_{2}\) с разным объемом выборки. Мы будем изменять количество выборок \(n\) в \(X_{1}\) и \(X_{2}\) при создании наших примеров. Уровни \(\beta\) были взяты из исследования по симуляции Fernández _et al._ (2001), тогда как количество истинных эффектов, \(p_{\gamma}\), за исключением Ex3, варьируется от \(5\) до \(16\). Наконец, симулированная ошибка дисперсии изменяется в диапазоне от \(0.05^{2}\) до \(2.5^{2}\) для изменения уровня сложности алгоритма поиска. На протяжении всего мы перечисляем только ненулевые \(\beta_{\gamma}\) и предполагаем, что \(\beta_{\gamma^{-}}=0^{T}\). Шесть примеров могут быть кратко описаны следующим образом: * **Ex1**: \(X=X_{1}\) - это матрица размером \(120\times 60\), где ответы моделируются из уравнения (1) с использованием \(\alpha=0\), \(\gamma=\left(21,37,46,53,54\right)^{T}\), \(\beta_{\gamma}=\left(2.5,0.5,-1,1.5,0.5\right)^{T}\), а \(\varepsilon\sim N\left(0,2^{2}I_{120}\right)\). Далее в нашей работе мы больше не будем ссылаться на свободный член \(\alpha\), так как, как описано в разделе 3.3 статьи, мы рассматриваем \(y\) с центрированием и, следовательно, результаты не меняются, если свободный член моделируется или нет. Это самый простой из наших примеров, однако, как указано в G&McC (1993), средняя попарная корреляция составляет около 0.5, что делает его уже трудным для анализа с использованием стандартных методов пошаговой регрессии. * **Ex2**: Этот пример прямо взят из N&G (2004), Пример 2, где впервые представлена идея комбинирования более простых "строительных блоков" для создания новой матрицы \(X\): в этом примере \(X=\left[X_{2}^{\left(1\right)}X_{2}^{\left(2\right)}\right]\) - это матрица размером \(300\times 30\), где \(X_{2}^{\left(1\right)}\) и \(X_{2}^{\left(2\right)}\) являются матрицами размером \(300\times 15\) и имеют такую же структуру, как \(X_{2}\). Кроме того, \(\gamma=\left(1,3,5,7,8,11,12,13\right)^{T}\), \(\beta_{\gamma}=\left(1.5,1.5,1.5,1.5,-1.5,1.5,1.5,1.5\right)^{T}\), и \(\varepsilon\sim N\left(0,2.5^{2}I_{300}\right)\). Мы выбрали этот пример по двум причинам: во-первых, поскольку корреляционная структура в \(X_{2}\) очень сложна, мы тестируем предложенный алгоритм при сильной и сложной корреляции между ковариациями; во-вторых, поскольку \(y\) не моделируется из второго "блока", нас интересует, будет ли предложенный алгоритм _не_ выбирать ни одну переменную, принадлежащую второй группе. * **Ex3**: Как в G&McC (1993), Пример 2, \(X=X_{1}\) - это матрица размером \(120\times 60\), \(\beta=\left(\beta_{1},\ldots,\beta{}_{60}\right)^{T}\), \(\left(\beta_{1},\ldots,\beta_{15}\right)=\left(0,\ldots,0\right)\), \(\left(\beta_{16},\ldots,\beta_{30}\right)=\left(1,\ldots,1\right)\), \(\left(\beta_{31},\ldots,\beta_{45}\right)=\left(2,\ldots,2\right)\), \(\left(\beta_{46},\ldots,\beta_{60}\right)=\left(3,\ldots,3\right)\), и \(\varepsilon\sim N\left(0,2^{2}I_{120}\right)\). Мотивацией этого примера является проверка способности предложенного алгоритма выбрать подмножество переменных, которое является большим по сравнению с \(p\), сохраняя способность _не_ выбирать любую из первых \(15\) переменных. * **Ex4**: Матрица плана \(X\), размером \(120\times 300\), строится следующим образом: сначала мы создаем новый "строительный блок" \(X_{3}\) размером \(120\times 60\), объединяя \(X_{2}\) и меньшую версию \(X_{1}\), \(X_{1}^{\ast}\), матрицу размером \(120\times 45\), смоделированную как \(X_{1}\), так что \(X_{3}=\left[X_{2}X_{1}^{\ast}\right]\) (размерность \(120\times 60\)). Затем мы размещаем рядом пять копий \(X_{3}\), \(X=\left[X_{3}^{\left(1\right)}X_{3}^{\left(2\right)}X_{3}^{\left(3\right)}X_{3 }^{\left(4\right)}X_{3}^{\left(5\right)}\right]\): новая матрица плана чередует блоки ковариаций с высокой и сложной корреляцией, как в G&McC (1997), с областями, где корреляция умеренная, как в G&McC (1993). Мы моделируем отклик, выбирая \(16\) переменных из \(X\), \(\gamma=\left(1,11,30,45,61,71,90,105,121,131,150,165,181,191,210,225\right)^{T}\), так что каждая пара переменных принадлежит либо к \(X_{2}\), либо к \(X_{1}\). Мы моделируем \(y\) с использованием \(\beta_{\gamma}=\left(2,-1,1.5,1,0.5,2,-1,1.5,1,0.5,2,-1,-1,1.5,1,0.5\right)^{T}\) и \(\varepsilon\sim N\left(0,2.5^{2}I_{120}\right)\). Этот пример является сложным с точки зрения корреляционной структуры, количества ковариаций \(p>n\) и различных уровней эффектов. * **Ex5**: Это самый сложный пример, который мы смоделировали, и он основан на идее загрязненных моделей. Матрица \(X\), размером \(200\times 1000\), опред Мы заканчиваем данный раздел, сообщая о том, как мы проводили эксперимент симуляции: каждый пример от Ex1 до Ex6 был воспроизведен 25 раз, и результаты, представленные для примеров Ex1 до Ex5, усредняются по 25 репликам. Для Ex6 изменения эффектов фиксируются, поэтому усреднение выполняется только для смешивающих свойств. ESSi с τ=1 был применен к каждому примеру/выборке, записывая посещенную последовательность γ₁ в течение 20,000 итераций после прогрева, состоящего из 2,000 итераций, необходимых для автоматической настройки размещения температуры, раздел 3.1. За исключением Ex2 и Ex3, где мы использовали равнодушный априори, p(γ) = (1/2)^p, мы анализировали остальные примеры, устанавливая E(p_γ) = 5 и V(p_γ) = E(p_γ)(1 - E(p_γ)/p), что соответствует биномиальному априори для p_γ. Чтобы определить чувствительность предложенного алгоритма к выбору E(p_γ), мы также проанализировали Ex1, установив E(p_γ) = 10 и 20. Более того, во всех примерах мы выбрали L = 5, а начальное значение γ было выбрано случайным образом. Два оставшихся гиперпараметра, а именно a_σ и b_σ, устанавливаются равными a_σ = 10^(-6) и b_σ = 10^(-3), как в Kohn et al. (2001), что соответствует относительно неинформативному априори. ### Смешивающие свойства ESS\({i}\) В этом разделе мы сообщаем о некоторых стилизованных фактах о производительности ESS\({i}\) с фиксированным значением \(\tau = 1\). На верхних панелях рисунка 5 показаны общие характеристики смешивания ESS\(i\) для одного из реплик Ex1. Как и ожидалось, цепочки, прикрепленные к более высоким температурам, показывают большую изменчивость. Хотя сходимость достигается в пространстве произведения \(\prod\nolimits_{l=1}^{L}\left[p\left(\gamma_{l}\left|y\right.\right)\right]^{1 /t_{l}}\), визуальным осмотром можно установить, что каждая цепь _постепенно_ достигает своего _равновесия_ по отношению к другим; более того, благодаря автоматической настройке размещения температуры во время прогрева, распределения их логарифмов апостериорных вероятностей хорошо перекрываются, что позволяет эффективно обмениваться информацией между цепями. Нижние панели рисунка 5 показывают график следов логарифма апостериорной вероятности и размера модели для реплики Ex4. Мы видим, что даже в случае \(p>n\) цепи смешиваются и хорошо перекрываются, между ними нет разрывов, автоматическая настройка лестницы температур способна значительно улучшить производительность алгоритма. Данная эффективная передача информации продемонстрирована в Таблице 4, которая показывает хорошие общие показатели приема для набора ходов, которые мы реализовали. Размер проблемы, кажется, не влияет на показатель приема оператора обмена (отложенного отклонения), который остается очень стабильным и близким к целевому значению: например, в Ex4 (p=300) и Ex6 (p=775), среднее значение и стандартное отклонение показателя приема составляют 0,517 (0,105) и 0,497 (0,072), в то время как в Ex5 (p=1,000) у нас есть 0,505 (0,013): большая изменчивость в Ex4 связана с размером модели p𝛾. Что касается операторов кроссовера, мы снова наблюдаем стабильность во всех примерах. Более того, в отличие от Jasra и др. (2007), когда \(p>n\), средняя степень принятия оператора кроссовера по пяти цепочкам достаточно стабильна и составляет от \(0.147\) (Ex4) до \(0.193\) (Ex6) (меньшее значение в Ex4 здесь снова вызвано \(p_{\gamma}\)): в рамках наших ограниченных экспериментов мы считаем, что хорошая производительность оператора кроссовера связана с оператором выбора и новым блочным кроссовером, см. Раздел 3.1. Некоторая дополнительная настройка температурной лестницы все еще может быть выполнена, так как есть указание на то, что с более высокой температурой цепи принимается меньше глобальных перемещений, см. Таблицу 5, где указаны вероятности обмена для каждой цепи. Обратите внимание, что наблюдаемая частота успешных обменов немного отличается от случая, когда соседние цепи выбираются для обмена случайным образом с равной вероятностью. Другие меры перекрытия между цепями (Лианг и Уонг, 2000; Иба, 2001), основанные на подходящем индексе вариации переменной \(f\left(\gamma\right)=\log p\left(y\left|\gamma\right.\right)+\log p\left( \gamma\right)\) на протяжении переборов, подтверждают хорошую производительность ESS\(i\). Опять же, некоторая нестабильность присутствует в цепях с высокой температурой, см. в Таблице 5 индекс перекрытия между цепями \(3,4\) и \(4,5\) в Примере 3 по 6. В Ex1 мы также исследуем влияние различных значений априорного среднего размера модели. Мы обнаружили, что средняя (стандартное отклонение в скобках) скорость принятия для оператора отказа отложиться на обмен составляет от \(0.493\) (\(0.043\)) до 0.500 (0.040) для разных значений априорного среднего размера модели, в то время как скорость принятия для оператора кроссовера составляет от \(0.249\) (\(0.021\)) до \(0.271\) (\(0.036\)). Эта сильная стабильность не удивительна, потому что автоматическая настройка изменяет лестницу температуры, чтобы компенсировать \(E\left(p_{\gamma}\right)\). Наконец, мы замечаем, что скорость принятия для локального перемещения, когда \(n>p\), увеличивается с увеличением значений априорного среднего размера модели, что показывает, что локально алгоритм движется более свободно с \(E\left(p_{\gamma}\right)=20\) по сравнению с \(E\left(p_{\gamma}\right)=5\). ### Производительность ESS\(i\) и сравнение с SSS #### Производительность ESS\(i\) Мы завершаем данный раздел, обсудив в подробностях общую производительность ESS\(i\) в отношении выбора правильных симулированных эффектов. В качестве первой меры производительности мы представляем для всех симулированных примеров маргинальную апостериорную вероятность включения, описанную в работах G&McC (1997) и Hans _et al._ (2007). Далее, для удобства обозначений, мы опускаем индекс цепи и обращаемся исключительно к первой цепи. Для точности, мы оцениваем маргинальную апостериорную вероятность включения следующим образом: \[\hat{p}(\gamma_{j}=1|y) \approx C^{-1}\sum_{t=1,\ldots,T}1_{ (\gamma_{j}^{(t)}=1)}(\gamma)p(y| \gamma^{(t)})p(\gamma^{(t)})\] (A.12) с \(C=\sum_{t=1,\ldots,T}p\left(y\left|\gamma^{\left(t\right)}\right.\right)p\left (\gamma^{\left(t\right)}\right)\) и \(T\) количество проходов после "burn-in". Размер постериорной модели также определяется так: \(p\left(p_{\gamma}\left|y\right.\right)\simeq C^{-1}\sum_{t=1,\ldots,T}1_{\left (\left|\gamma^{\left(t\right)}\right|=p_{\gamma}\right)}\left(\gamma\right)p \left(y\left|\gamma^{\left(t\right)}\right.\right)p\left(\gamma^{\left(t\right )}\right)\), с \(C\) как раньше. Кроме того, мы также будем вычислять интерквартильный размах (A.12) по всем повторам в качестве показателя изменчивости при построении графиков маргинальной включенности постериорной вероятности для наших симулированных примеров. Для того чтобы тщательно сравнить предложенный алгоритм ESS с алгоритмом SSS (Ханс _et al., 2007), мы также представляем некоторые другие показатели производительности, основанные на \(p\left(\gamma\left|y\right.\right)\) и \(R_{\gamma}^{2}\): сначала мы упорядочиваем \(p\left(\gamma\left|y\right.\right)\) в убывающем порядке и записываем индикатор \(\gamma\), соответствующий максимальному значению, а также \(1,000\) наибольших \(p\left(\gamma\left|y\right.\right)\) (после отбрасывания начальных значений). Имея указанный набор скрытых двоичных векторов, мы затем вычисляем соответствующий \(R_{\gamma}^{2}\), приводящий к " \(R_{\gamma}^{2}\): \(\max p\left(\gamma\left|y\right.\right)\) ", а также средний \(R_{\gamma}^{2}\) по \(1,000\) наибольшим \(p\left(\gamma\left|y\right.\right)\), " \(\overline{R_{\gamma}^{2}}\): \(1,000\) наибольших \(p\left(\gamma\left|y\right.\right)\) ", оба показателя усреднены по повторам. Кроме того, отслеживается фактическая способность алгоритма достигать областей высокой апостериорной вероятности и удерживаться на них: учитывая последовательность \(1,000\) лучших \(\gamma\) (основанных на \(p\left(\gamma\left|y\right.\right)\)), стандартное отклонение соответствующих \(R_{\gamma}^{2}\) показывает, насколько стабильна стратегия поиска, по крайней мере, для наиболее ранжированных (не уникальных) апостериорных вероятностей: усреднение по повторам предоставляет эвристические меры "стабильности" алгоритма. Наконец, мы сообщаем среднее время вычислений (в минутах) по повторам для ESS\(i\), написанного на языке Matlab и запущенного на компьютере с процессором 2 МГц и 1.5 Гб оперативной памяти, а также для версии SSS 2.0 на том же компьютере. #### Сравнение с SSS На рисунке 6 представлена маргинальная апостериорная вероятность включения для ESS\(i\) с \(\tau=1\), усредненная по повторам, а также, как мера изменчивости, межквартильный размах, синие левые треугольники и вертикальная синяя сплошная линия соответственно. В целом, предикторы с ненулевым эффектом имеют высокую маргинальную апостериорную вероятность включения во всех примерах: например, в примере 3, рисунок 6 (а), предложенный алгоритм ESS\(i\), синий левый треугольник, идеально выбирает последние 45 предикторов, в то время как первые 15, не влияющие на \(y\), получают небольшую маргинальную апостериорную вероятность. Интересно отметить, что эта группа предикторов, \(\left(\beta_{1},\ldots,\beta_{15}\right)=\left(0,\ldots,0\right)\), хотя и правильно распознана как не имеющая влияния на \(y\), все же имеет некоторую изменчивость между повторами, вертикальной синей сплошной линией: однако это неудивительно, поскольку независимые априорные распределения менее подходят для ситуаций, когда все предикторы слабо-сильно коррелированы, как в этом симулированном примере. С другой стороны, второй набор предикторов с небольшими эффектами, \(\left(\beta_{16},\ldots,\beta_{30}\right)=\left(1,\ldots,1\right)\), однозначно обнаруживается. Способность ESS\(i\) выбирать переменные с небольшими эффектами также явно проявляется в примере 6, рисунок 6 (д), где два наименьших коэффициента, \(\beta_{2}=0.112\) и \(\beta_{10}=0.950\) (второй и последний, справа налево), получают от высокой до очень высокой маргинальную апостериорную вероятность (и аналогично для других повторов, данные не показаны). Однако в некоторых случаях пропускаются некоторые предикторы с малыми эффектами (например, в примере 4, рисунок 6 (б), последний симулированный эффект, также самый маленький, \(\beta_{16}=0.5\), не обнаруживается). В этой ситуации, однако, вертикальная синяя сплошная линия указывает, что для некоторых повторов ESS\(i\) способен присваивать малые значения маргинальной апостериорной вероятности, что свидетельствует о том, что ESS\(i\) полностью исследует все модели. Все маркированные на всех изображениях Рисунка 5 медиана и интерквартильный размах между повторениями \(p\left(\gamma_{j}=1\left|y\right.\right)\), \(j=1,\ldots,p\), для SSS, красные правильные треугольники и вертикальная красная пунктирная линия соответственно. Мы видим, что в целом существует хорошее согласие между двумя алгоритмами, при этом ESS\(i\) может более полно исследовать пространство моделей и, в частности, находить небольшие эффекты, что приводит к постериорному размеру модели, близкому к истинному. Например, в Ex3, Рисунок 6 (a), где последние 30 ковариативных переменных объясняют большую часть \(R_{\gamma}^{2}\), у SSS возникают проблемы с обнаружением \(\left(\beta_{16},\ldots,\beta_{30}\right)\), в то время как в Ex6 пропускается \(\beta_{2}=0.112\), наименьший эффект, и удивительным образом также происходит пропуск \(\beta_{4}=-2.595\) при назначении очень маленькой маргинальной постериорной вероятности (и в общем для маленьких эффектов в большинстве повторов, данные не показаны). Однако наиболее явное различие между ESS\(i\) и SSS присутствует в Ex5: как и для ESS\(i\), SSS не обнаруживает три эффекта "модели 1", но, кроме того, \(\beta_{4}=1\), \(\beta_{7}=-1\) и \(\beta_{8}=1.5\) также имеют очень низкую маргинальную постериорную вероятность, красные правильные треугольники, с большой изменчивостью в повторах, вертикальная красная пунктирная линия. Более того, как уже отмечалось, ESS\(i\) способен захватывать самый большой коэффициент "модели 2", в то время как SSS полностью пропускает все зашумленные эффекты. В Ex1 и Ex2 нет заметных различий между ESS\(i\) и SSS в отношении маргинальной постериорной вероятности, в то время как в Ex4 SSS показывает большую изменчивость в \(p\left(\gamma_{j}=1\left|y\right.\right)\) (красные пунктирные вертикальные линии по сравнению с синими сплошными вертикальными линиями) для некоторых ковариативных переменных, которые получают наивысшую маргинальную постериорную вероятность. В отличие от различий в маргинальной апостериорной вероятности включения, существует общее согласие между двумя алгоритмами в отношении некоторых мер качества подгонки и стабильности, см. Таблицу 6. Опять же, неудивительно, основное различие видно в Ex5, где ESS\(i\) с \(\tau=1\) достигает лучшего \(R_{\gamma}^{2}\) как для максимального, так и для 1000 наибольших \(p\left(\gamma\left|y\right.\right)\). SSS показывает большую стабильность во всех примерах, кроме последнего: это было ожидаемо, так как одной из ключевых особенностей SSS является его способность быстро перемещаться к правильной модели и стойко на ней находиться (Hans _et al._, 2007), но это затрудняет его способность исследовать далеко удаленные модели с конкурирующими \(R_{\gamma}^{2}\), как в Ex5. Обратите внимание, что ESS\(i\) показывает небольшое улучшение \(R_{\gamma}^{2}\) во всех имитационных примерах. Это связано с способностью ESS\(i\) обнаружить некоторые слабые эффекты, которые SSS упускает, см. Рисунок 6. Наконец, ESS\(i\) показывает замечательное превосходство в отношении вычислительного времени, особенно когда имитационное (и оцениваемое) \(p_{\gamma}\) является большим (в других имитационных примерах, не показанных здесь, мы установили, что это всегда верно, когда \(p_{\gamma}\gtrsim 10\)): объяснение заключается в количестве различных моделей, которые SSS и ESS\(i\) оценивают на каждой итерации. Действительно, SSS оценивает \(p+p_{\gamma}\left(p-p_{\gamma}\right)\), где \(p_{\gamma}\) - размер текущей модели, в то время как ESS\(i\) в теории анализирует равное количество моделей, \(pL\), но, когда \(p>n\), фактическое количество оцениваемых моделей существенно сокращается благодаря нашему сэмплеру FSMH. Только в одном случае SSS опережает ESS\(i\) по вычислительному времени (Ex5), но в этом случае SSS явно недооценивает имитационную модель и, следовательно, выполняет меньше оценок, чем было бы необходимо для правильного исследования пространства моделей. В заключение, мы видим, что богатый набор перемещений и использование параллельных цепей делает ESS устойчивым для работы с сложными пространствами ковариат и конкурентоспособным по отношению к передовому алгоритму поиска. ## Ссылки Абрамовиц, М. и Стегун, И. (1970). _Справочник по математическим функциям_. Нью-Йорк: Dover Publications, Inc. Альтшулер, Д., Брукс, Л.Д., Чакраварти, А., Коллинз, Ф.С., Дэли, М.Д. и Доннелли, П. (2005). Карта гаплотипов генома человека. _Nature_, **437**, 1299-1320. Bae, N. и Mallick, B.K. (2004). Выбор генов с использованием двухуровневой иерархической байесовской модели. _Bioinformatics_, **20**, 3423-3430. Браун, П.Дж., Ваннуччи, М. и Фирн, Т. (1998). Многомерный байесовский отбор переменных и прогнозирование. Журнал "R. Statist. Soc. B", 60, 627-641. Calvo, F. (2005) Всеобменное параллельное охлаждение. _J. Chem. Phys._, **123**, 1-7. Chipman, H. (1996). Байесовский выборка с переменными для связанных предикторов. _Canad. J. Statist._, **24**, 17-36. Chipman, H., George, E.I. и McCulloch, R.E. (2001). Практическая реализация байесовского выбора модели (с обсуждением). В книге _Выбор модели_ (P. Lahiri, ред.), 66-134. IMS: Beachwood, OH. Clyde, M. и George, E. I. (2004). Model uncertainty. _Statist. Sci._, **19**, 81-94. Cui, W. и George, E.I. (2008). Сравнение эмпирического Байеса и полностью Байесовского выбора переменных. _J. Stat. Plan. Inf._, **138**, 888-900. Делапортас, П., Форстер, Дж. и Нтзуфрас, И. (2002). О байесовской модели и выборе переменных с использованием MCMC. _Statist. Comp._, **12**, 27-36. Fernández, C., Ley, E. и Steel, M.F.J. (2001). Prior-поверка для поключения метода средневзвешенных байесовских моделей. Журнал "J. Econometrics" №75, 317-343. Джордж, И. и Маккалоч, Р.Е. (1993). Выбор переменных с использованием сэмплирования Гиббса. _J. Am. Statist. Assoc._, **88**, 881-889. Джордж, И.И. и МакКаллох, Р.Е. (1997). Подходы к байесовскому выбору переменных. _Stat. Sinica_, **7**, 339-373. Geweke, J. (1996). Выбор переменных и сравнение моделей в регрессии. В _Байесовская статистика 5, Сборник трудов 5-го международного совещания_ (ред. J.M. Bernardo, J.O. Berger, A.P. Dawid и A.F.M. Smith), 609-20. Издательство Claredon: Оксфорд, Великобритания. Госвами, Г. и Лю, Дж. С. (2007). Об учебных стратегиях для эволюционного Монте-Карло. Statist. Comp., 17, 23-38. Gramacy, R.B, J. Samworth, R.J. и King, R. (2007). Importance Tempering. Технический доклад. Доступно по адресу: http://arxiv.org/abs/0707.4242 Зеленые, П. и Мира, А. (2001). Отложенное отклонение в обратном переходе Метрополиса-Гастингса. _Биометрика_, **88**, 1035-1053. Iba, Y. (2001). Расширенный ансамбль Монте-Карло. _Int. J. Mod. Phys., C_, **12**, 623-656. Hans, C., Dobra, A. и West, M. (2007). Shotgun Stochastic Search for “large \(p\)” regression. _J. Am. Statist. Assoc._, **102**, 507-517. Hubner, N. _et al._ (2005). Интегрированный транскрипционный профилирование и связанный анализ для идентификации генов, лежащих в основе заболеваний. _Nat. Genet._, **37**, 243-253. Kohn, R., Smith, M. и Chan, D. (2001). Непараметрическая регрессия с использованием линейных комбинаций базисных функций. _Statist. Comp._, **11**, 313-322. Jasra, A., Stephens, D.A. и Holmes, C. (2007). Монте-Карло методы на основе обратимых прыжков с цепями Маркова в популяционных исследованиях. _Biometrika_, **94**, 787-807. Liang, F., Paulo, R., Molina, G., Clyde, M.A. и Berger, J.O. (2008). Смеси \(g\)-приоров для байесовского выбора переменных. _J. Am. Statist. Assoc._, **481**, 410-423. Liang, F. и Wong, W.H. (2000). Evolutionary Monte Carlo: применение к выборке модели \(C_{p}\) и задаче смены точки. _Stat. Sinica_, **10**, 317-342. Лью, Дж.С. (2001). _Методы Монте-Карло в научных вычислениях_. Спрингер: Нью-Йорк. Madigan, Д. и York, Я. (1995). Байесовские графические модели для дискретных данных. _Int. Statist. Rev._, **63**, 215-232. Натараджан, Р. и Маккалох. (1998). Гиббс-отсчёт с рассеянными адекватными приорами: правильный подход к выводу на основе данных?, _J. Comp. Graph. Statist._, **7**, 267-277. Nott, D.J. и Green, P.J. (2004). Байесовский отбор переменных и алгоритм Сведсена-Ванга. _J. Comp. Graph. Statist._, **13**, 141-157. Робертс, Г.О. и Розенталь, Дж.С. (2008). Пример адаптивного МСМК. Тех. докл. Доступно по адресу: http://www.probability.ca/jeff/research.html Тьерни, Л. и Кадан, Дж.Б. (1986). Точные приближения для апостериорных моментов и маргинальных плотностей. _J. Am. Statist. Assoc._, **81**, 82-86. Wilson, M.A., Иверсен, Э.С., Клайд, М.А., Шмидлер, С.К. и Шилдкраут, Дж.М. (2009). Поиск байесовой модели и многоуровневое рассуждение для исследований ассоциации однонуклеотидных полиморфизмов. Тех. док. Доступно по адресу: Перевод маркдауна с английского на русский. Сохранение формул: http://arxiv.org/abs/0908.1144 Zellner, A. (1986). Оценка априорных распределений и байесовский анализ регрессии с \(g\)-априорными распределениями. В _Байесовский вывод и техники принятия решений - очерки в честь Бруно де Финетти_ (П. К. Гоэл и А. Зеллнер, ред.), 233-243. Амстердам: North-Holland. Zellner, A. и Siow, A. (1980). Posterior odds ratios для выбранных гипотез регрессии. В _ Bayesian Statistics, Proc. 1-ого Интерн. собрания_ (J.M. Bernardo, M.H. De Groot, D.V. Lindley и A.F.M. Smith, ред.), 585-603. Валенсия: издательство Университета. [РИСУНОК:Ax1.F1][КОНЕЦРИСУНКА] [FIGURE:Ax1.F2][ENDFIGURE] - [Изображение:Ax1.F2] [РИСУНОК:Ax1.F3][КОНЕЦРИСУНКА] [FIGURE:Ax1.F4][ENDFIGURE] - [ИЗОБРАЖЕНИЕ:Ax1.F4][КОНЕЦ ИЗОБРАЖЕНИЯ] [РИСУНОК:Ax1.F5][КОНЕЦРИСУНКА] [FIGURE:Ax1.F6][ENDFIGURE] - [ФИГУРА:Ax1.F6][КОНЕЦФИГУРЫ] [TABLE:Ax1.T1][ENDTABLE] [TABLE:Ax1.T2][ENDTABLE] [TABLE:Ax1.T3][ENDTABLE] [TABLE:Ax1.T4][ENDTABLE] [TABLE:Ax1.T5][ENDTABLE] [TABLE:Ax1.T6][ENDTABLE] Translate Markdown на русский язык.

# Blueshift of the surface plasmon resonance in silver nanoparticles: substrate effects Søren Raza,\({}^{1,2}\) Wei Yan,\({}^{1,3}\) Nicolas Stenger,\({}^{1,3}\) Martijn Wubs,\({}^{1,3}\) and N. Asger Mortensen\({}^{1,3,{\dagger}}\) ###### Abstract We study the blueshift of the surface plasmon (SP) resonance energy of isolated Ag nanoparticles with decreasing particle diameter, which we recently measured using electron energy loss spectroscopy (EELS) [1]. As the particle diameter decreases from 26 down to 3.5 nm, a large blueshift of 0.5 eV of the SP resonance energy is observed. In this paper, we base our theoretical interpretation of our experimental findings on the nonlocal hydrodynamic model, and compare the effect of the substrate on the SP resonance energy to the approach of an effective homogeneous background permittivity. We derive the nonlocal polarizability of a small metal sphere embedded in a homogeneous dielectric environment, leading to the nonlocal generalization of the classical Clausius–Mossotti factor. We also present an exact formalism based on multipole expansions and scattering matrices to determine the optical response of a metal sphere on a dielectric substrate of finite thickness, taking into account retardation and nonlocal effects. We find that the substrate-based calculations show a similar-sized blueshift as calculations based on a sphere in a homogeneous environment, and that they both agree qualitatively with the EELS measurements. \({}^{1}\)Department of Photonics Engineering, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark \({}^{2}\)Center for Electron Nanoscopy, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark \({}^{3}\)Center for Nanostructured Graphene (CNG), Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark \({}^{\dagger}\)[email protected] (240.6680) Surface plasmons. (250.5403) Plasmonics. (160.4236) Nanomaterials. (000.1600) Classical and quantum physics. (260.3910) Metal optics. ## References * [1] S. Raza, N. Stenger, S. Kadkhodazadeh, S. V. Fischer, N. Kostesha, A.-P. Jauho, A. Burrows, M. Wubs, and N. A. Mortensen, “Blueshift of the surface plasmon resonance in silver nanoparticles studied with EELS,” Nanophotonics **2**, 131–138 (2013). * [2] G. Mie, “Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen,” Ann. Phys. **330**, 377–445 (1908). * [3] S. A. Maier, _Plasmonics: Fundamentals and Applications_ (Springer, New York, 2007). * [4] N. D. Lang and W. Kohn, “Theory of metal surfaces: Charge density and surface energy,” Phys. Rev. B **1**, 4555–4568 (1970). * [5] A. Boardman, B. Paranjape, and R. Teshima, “The effect of structure on surface plasmons,” Surf. Sci. **49**, 275–292 (1975). * [6] A. J. Bennett, “Influence of the electron charge distribution on surface-plasmon dispersion,” Phys. Rev. B **1**, 203–207 (1970). * [7] P. Apell, “A simple derivation of the surface contribution to the reflectivity of a metal, and its use in the Van der Waals interaction,” Phys. Scr. **24**, 795 (1981). * [8] P. J. Feibelman, “Surface electromagnetic fields,” Prog. Surf. Sci. **12**, 287–407 (1982). * [9] R. Ruppin, “Optical properties of a plasma sphere,” Phys. Rev. Lett. **31**, 1434–1437 (1973). * [10] A. D. Boardman and B. V. Paranjape, “The optical surface modes of metal spheres,” J. Phys. F: Met. Phys. **7**, 1935 (1977). * [11] P. Apell and Å. Ljungbert, “A general non-local theory for the electromagnetic response of a small metal particle,” Phys. Scr. **26**, 113 (1982). * [12] C. Schwartz and W. L. Schaich, “Hydrodynamic models of surface plasmons,” Phys. Rev. B **26**, 7008–7011 (1982). * [13] A. I. Fernández-Domínguez, A. Wiener, F. J. García-Vidal, S. A. Maier, and J. B. Pendry, “Transformation-optics description of nonlocal effects in plasmonic nanostructures,” Phys. Rev. Lett. **108**, 106802 (2012). * [14] C. David and F. J. García de Abajo, “Spatial nonlocality in the optical response of metal nanoparticles,” J. Phys. Chem. C **115**, 19470–19475 (2012). * [15] G. Toscano, S. Raza, A.-P. Jauho, N. A. Mortensen, and M. Wubs, “Modified field enhancement and extinction in plasmonic nanowire dimers due to nonlocal response,” Opt. Express **20**, 4176–4188 (2012). * [16] C. Ciracì, R. T. Hill, J. J. Mock, Y. Urzhumov, A. I. Fernández-Domínguez, S. A. Maier, J. B. Pendry, A. Chilkoti, and D. R. Smith, “Probing the ultimate limits of plasmonic enhancement,” Science **337**, 1072–1074 (2012). * [17] U. Kreibig and C. Fragstein, “The limitation of electron mean free path in small silver particles,” Z. Physik **224**, 307–323 (1969). * [18] L. Genzel, T. P. Martin, and U. Kreibig, “Dielectric function and plasma resonance of small metal particles,” Z. Phys. B **21**, 339–346 (1975). * [19] P. Apell and D. R. Penn, “Optical properties of small metal spheres: Surface effects,” Phys. Rev. Lett. **50**, 1316–1319 (1983). * [20] O. Keller, M. Xiao, and S. Bozhevolnyi, ‘‘Optical diamagnetic polarizability of a mesoscopic metallic sphere: transverse self-field approach,” Opt. Comm. **102**, 238–244 (1993). * [21] U. Kreibig and L. Genzel, “Optical absorption of small metallic particles,” Surf. Sci. **156**, 678–700 (1985). * [22] K.-P. Charlé, W. Schulze, and B. Winter, “The size dependent shift of the surface-plasmon absorption-band of small spherical metal particles,” Z. Phys. D **12**, 471–475 (1989). * [23] H. Hövel, S. Fritz, A. Hilger, U. Kreibig, and M. Vollmer, “Width of cluster plasmon resonances: Bulk dielectric functions and chemical interface damping,” Phys. Rev. B **48**, 18178–18188 (1993). * [24] J. Tiggesbäumker, L. Köller, K.-H. Meiwes-Broer, and A. Liebsch, “Blue shift of the Mie plasma frequency in Ag clusters and particles,” Phys. Rev. A **48**, R1749–R1752 (1993). * [25] S. Berciaud, L. Cognet, P. Tamarat, and B. Lounis, ‘‘Observation of intrinsic size effects in the optical response of individual gold nanoparticles,” Nano Lett. **5**, 515–518 (2005). * [26] F. Ouyang, P. Batson, and M. Isaacson, “Quantum size effects in the surface-plasmon excitation of small metallic particles by electron-energy-loss spectroscopy,” Phys. Rev. B **46**, 15421–15425 (1992). * [27] J. A. Scholl, A. L. Koh, and J. A. Dionne, “Quantum plasmon resonances of individual metallic nanoparticles,” Nature **483**, 421 (2012). * [28] A. Boardman, _Electromagnetic Surface Modes. Hydrodynamic theory of plasmon-polaritons on plane surfaces._ (John Wiley and Sons, Chichester, 1982). * [29] P. Apell, “The electromagnetic field near a metal surface in the semi-classical infinite barrier model,” Phys. Scr. **17**, 535 (1978). * [30] L. Mulfinger, S. D. Solomon, M. Bahadory, A. Jeyarajasingam, S. A. Rutkowsky, and C. Boritz, “Synthesis and study of silver nanoparticles,” J. Chem. Educ. **84**, 322 (2007). * [31] A. Boardman and R. Ruppin, “The boundary conditions between spatially dispersive media,” Surf. Sci. **112**, 153–167 (1981). * [32] D. J. Griffiths, _Introduction to Electrodynamics (3rd Edition)_ (Benjamin Cummings, 1998). * [33] F. Bloch, “Bremsvermögen von Atomen mit mehreren Elektronen,” Z. Phys. A **81**, 363–376 (1933). * [34] S. Raza, G. Toscano, A.-P. Jauho, M. Wubs, and N. A. Mortensen, “Unusual resonances in nanoplasmonic structures due to nonlocal response,” Phys. Rev. B **84**, 121412(R) (2011). * [35] G. Toscano, S. Raza, W. Yan, C. Jeppesen, S. Xiao, M. Wubs, A.-P. Jauho, S. I. Bozhevolnyi, and N. A. Mortensen, “Nonlocal response in plasmonic waveguiding with extreme light confinement,” Nanophotonics **2**, 161–166 (2013). * [36] F. Sauter, “Der Einfluß von Plasmawellen auf das Reflexionsvermögen von Metallen (I),” Z. Physik **203**, 488–494 (1967). * [37] F. Forstmann and H. Stenschke, “Electrodynamics at metal boundaries with inclusion of plasma waves,” Phys. Rev. Lett. **38**, 1365–1368 (1977). * [38] G. Barton, “Some surface effects in the hydrodynamic model of metals,” Rep. Prog. Phys. **42**, 963 (1979). * [39] J. D. Jackson, _Classical electrodynamics_ (Wiley, 1998), 3rd ed. * [40] I. Villo-Perez, Z. Mišković, and N. Arista, “Plasmon spectra of nano-structures: A hydrodynamic model,” in “Trends in Nanophysics,” , V. Bârsan and A. Aldea, eds. (Springer Berlin Heidelberg, 2010), Engineering Materials, pp. 217–254. * [41] I. Lindau and P. O. Nilsson, “Experimental evidence for excitation of longitudinal plasmons by photons,” Phys. Lett. A **31**, 352–353 (1970). * [42] K.-P. Charlé, L. König, S. Nepijko, I. Rabin, and W. Schulze, “The surface plasmon resonance of free and embedded Ag-clusters in the size range 1,5 nm \(<\) D \(<\) 30 nm,” Cryst. Res. Technol. **33**, 1085–1096 (1998). * [43] W. Yan et al., in preparation (2013). * [44] T. Bååk, “Silicon oxynitride; a material for GRIN optics,” Appl. Opt. **21**, 1069–1072 (1982). * [45] A. D. Rakić, A. B. Djurišić, J. M. Elazar, and M. L. Majewski, “Optical properties of metallic films for vertical-cavity optoelectronic devices.” Appl. Opt. **37**, 5271 (1998). * [46] R. Ruppin, “Surface modes and optical absorption of a small sphere above a substrate,” Surf. Sci. **127**, 108–118 (1983). * [47] A. Liebsch, “Surface-plasmon dispersion and size dependence of Mie resonance: silver versus simple metals,” Phys. Rev. B **48**, 11317–11328 (1993). * [48] R. Carmina Monreal, T. J. Antosiewicz, and S. P. Apell, “Plasmons do not go that quantum,” arXiv:1304.3023 (2013). ## 1 Introduction The use of metal nanoparticles to create astonishing colors in stained glass dates back to ancient Roman times. However, the mechanism behind the color generation was not fully understood until Mie in 1908 rigorously and exactly solved Maxwell’s electrodynamical equations for the problem of plane wave scattering off a sphere [2]. From Mie’s solution it follows that resonant modes of the metal sphere, which we now refer to as localized SPs [3], give rise to large absorption cross sections at specific wavelengths, resulting in the colorful stained glass. In Mie’s treatment of the problem it is assumed that the material properties of the sphere can be described by a single frequency-dependent function, the local-response dielectric function \(\varepsilon(\omega)\). While in most cases a classical treatment based on the dielectric function is justified, important effects due to surface structure [4, 5, 6, 7, 8], nonlocal response [9, 10, 11, 12, 13, 14, 15, 16] and quantum size effects [17, 18, 19, 20] manifest themselves in the response of metal nanoparticles, when the particle sizes are below \(\sim 10\) nm. Many experiments on tiny nanoparticles using both optical measurements [21, 22, 23, 24, 25] and electron energy-loss studies [26, 27, 1] have shown that the classical approach is insufficient to describe the experimental observations. The interpretation of these results has been based on semi-classical models, such as the nonlocal hydrodynamic [28] and semi-classical infinite barrier (SCIB) [29] approaches, or more complicated quantum calculations using density functional theory [4]. Recently, we performed EELS on chemically synthesized Ag nanoparticles with diameters ranging from 3.5 to 26 nm [1]. We observed a large blueshift of the localized SP resonance energy from 3.2 eV to 3.7 eV, when the particle size decreased. We interpreted these non-classical observations using two different semi-classical models, the hydrodynamic model and the model presented by Keller et al. [20], which both only qualitatively could explain the observations. In this paper, we focus on the hydrodynamic model and derive the nonlocal polarizability of a hydrodynamic sphere in a homogeneous environment, which leads to the nonlocal generalization of the Clausius–Mossotti factor. We also study the effect of the substrate on the resonance energy of the nanoparticle. Specifically, we develop an exact formalism to calculate the optical response of a metal sphere on a dielectric substrate of finite thickness, taking into account both retardation and nonlocal response. The theoretical calculations are compared to the EELS measurements. ## 2 Experiment: electron energy loss spectroscopy The silver nanoparticles are chemically synthesized [30] and afterwards stabilized in an aqueous solution with borohydride ions to prevent aggregation. Subsequently, the solution with nanoparticles is deposited on a plasma-cleaned 10 nm thick Si\({}_{3}\)N\({}_{4}\) TEM membrane purchased from TEMwindows.com. The mean particle diameter is 12 nm with a broad size distribution from 2 nm up to 30 nm, see Fig. 1, which gives us the advantage of being able to perform all of the measurements on the same sample. The EELS measurements are performed with a FEI Titan transmission electron microscope (TEM) equipped with a monochromator and a probe aberration corrector. The microscope is operated in scanning TEM (STEM) mode at an acceleration voltage of 120 kV, providing a probe diameter of 0.5 nm and a zero-loss peak width of \(0.15\pm 0.05\) eV. To enhance the excitation of the SP, the EELS spectra are acquired by directing the electron probe to the surface of the silver nanoparticle (aloof trajectory). Details on the data analysis and further experimental information can be found in Ref. [1]. [FIGURE:S2.F1][ENDFIGURE] ## 3 Theory: hydrodynamic model In the following theoretical approaches we will assume that the shape of the nanoparticles can be approximated to be spherical. Details and discussion about this approximation can be found in Ref. [1]. Here, we note from the TEM images in Fig. 1(b-f) that the overall shape of the nanoparticles is spherical, especially for particle sizes below 10 nm in diameter, which justifies our approximation. We base the interpretation of our experimental results on the hydrodynamic model. We first derive the exact nonlocal polarizability of a metal sphere embedded in a homogeneous material, thereby generalizing the well-known Clausius–Mossotti factor to nonlocal response. The free electrons of the sphere are described by the semiclassical hydrodynamic model, which takes into account nonlocal response but neglects the spill-out of the electrons outside the spheres due to the finiteness of their confining potential. Secondly, the effect of the substrate is taken into account. Here, we present an exact formalism to calculate the retarded optical response of a sphere with hydrodynamic nonlocal response, on a dielectric substrate of finite thickness. The starting point of the hydrodynamic model is Maxwell’s equations in terms of the free-electron density \(n\) and free-electron current \(\mathbf{J}\)[28, 31, 32] \[\mathbf{\nabla}\cdot\mathbf{D} =-en,\] (1a) \[\mathbf{\nabla}\cdot\mathbf{H} =0,\] (1b) \[\mathbf{\nabla}\times\mathbf{E} =i\omega\mu_{0}\mathbf{H},\] (1c) \[\mathbf{\nabla}\times\mathbf{H} =-i\omega\mathbf{D}+\mathbf{J},\] (1d) where the constitutive relation \(\mathbf{B}=\mu_{0}\mathbf{H}\) for non-magnetic materials has been utilized. Here, we introduce the polarization effects due to the bound charges through the constitutive relation for the displacement field \(\mathbf{D}=\varepsilon_{0}\varepsilon_{\infty}\mathbf{E}\), where \(\varepsilon_{\infty}\) in general is frequency-dependent and takes into account those polarization effects that are not due to the free electrons, such as interband transitions. The continuity equation, which connects the free-electron density and the free-electron current, follows directly from Eqs. (1a) and (1d), \[\mathbf{\nabla}\cdot\mathbf{J}=-i\omega en.\] (2) To complete the description of the electromagnetic response of the metal, a relation which connects the free-electron current to the electric field is needed. To this end, we consider the linearized nonlocal hydrodynamic equation [28, 33], which in its real-space formulation becomes [15, 34, 35] \[\frac{\beta^{2}}{\omega(\omega+i\gamma)}\mathbf{\nabla}\left( \mathbf{\nabla}\cdot\mathbf{J}\right)+\mathbf{J}=\varepsilon_{0}\sigma\mathbf{ E},\] (3) where \(\sigma=i\omega_{\textsc{p}}^{2}/(\omega+i\gamma)\) is the classical Drude conductivity, and \(\beta^{2}=3/5v_{\textsc{f}}^{2}\) with \(v_{\textsc{f}}\) being the Fermi velocity. Within a hydrodynamic description the pressure of the electron gas is included, which gives rise to the presence of compression (longitudinal) waves and leads to spatial dispersion that is observable in truly nanoplasmonic systems. Equations (1-3) constitute the basic set of equations within the retarded hydrodynamic approach. At an interface between two materials, these equations are supplemented by boundary conditions (BCs). In this study we consider only metal-dielectric interfaces, where Maxwell’s BCs must be augmented by a single additional boundary condition (ABC) which states that the normal component of the free-electron current density must vanish [31, 34, 36, 37, 38]. The ABC can be derived as a consequence of neglecting the spill-out of electrons. ### Hydrodynamic sphere in homogeneous environment: nonlocal Clausius–Mossotti factor We consider a small isotropic metal sphere of radius \(R\) embedded in a homogeneous dielectric environment with permittivity \(\varepsilon_{\textsc{b}}\). The polarizability \(\alpha\) of this sphere is a well-known result in classical optics [3, 39] and is given by \[\alpha=4\pi R^{3}\frac{\varepsilon_{\textsc{d}}-\varepsilon_{ \textsc{b}}}{\varepsilon_{\textsc{d}}+2\varepsilon_{\textsc{b}}},\] (4) where \(\varepsilon_{\textsc{d}}=\varepsilon_{\infty}-\omega_{\textsc{p}}^{2}/(\omega^ {2}+i\gamma\omega)\) is the classical Drude permittivity. The factor \((\varepsilon_{\textsc{d}}-\varepsilon_{\textsc{b}})/(\varepsilon_{\textsc{d}}+ 2\varepsilon_{\textsc{b}})\) is called the Clausius–Mossotti factor and notice that it is independent of the sphere radius. The polarizability is derived in the quasistatic approximation under the assumption of a static surrounding electric field, thus neglecting spatial variations in the exciting electric field. Our goal is now to derive a generalization to this formula, taking hydrodynamic nonlocal response of the sphere into account. We begin by introducing the electric and current scalar potentials \(\phi\) and \(\psi\), respectively, defined as \[\mathbf{E}=-\mathbf{\nabla}\phi,\hskip 28.452756pt\mathbf{J}=- \mathbf{\nabla}\psi.\] (5) By inserting Eq. (5) into the hydrodynamic Eqs. (1-3), it can straightforwardly be shown that the scalar potentials inside the metal sphere are governed by the equations [40] \[\left(\nabla^{2}+k_{\textsc{nl}}^{2}\right)n=0,\] (6a) \[\nabla^{2}\phi=\tfrac{e}{\varepsilon_{0}\varepsilon_{\infty}}n,\] (6b) \[\psi=\tfrac{1}{i\omega-\gamma}\left(\varepsilon_{0}\omega_{ \textsc{p}}^{2}\phi-e\beta^{2}n\right),\] (6c) where the nonlocal longitudinal wave vector is given as \(k_{\textsc{nl}}^{2}=(\omega^{2}+i\omega\gamma-\omega_{\textsc{p}}^{2}/ \varepsilon_{\infty})/\beta^{2}\). In the surrounding dielectric, the current density \(\mathbf{J}\) and electron density \(n\) vanish, and the electric scalar potential must instead satisfy the usual Laplace equation \(\nabla^{2}\phi=0\). Finally, Maxwell’s BCs and the hydrodynamic ABC for the scalar potentials translate into \[\phi^{\text{in}}=\phi^{\text{out}},\hskip 28.452756pt\varepsilon_ {\infty}\frac{\partial\phi^{\text{in}}}{\partial r}=\varepsilon_{\textsc{b}} \frac{\partial\phi^{\text{out}}}{\partial r},\hskip 28.452756pt\frac{\partial \psi^{\text{in}}}{\partial r}=0,\] (7) where _in_ and _out_ refers to inside and outside the metal, respectively. The general solutions to the electric scalar potential and free-electron density inside and outside the sphere are \[n^{\text{in}} =\sum_{l,m}A_{l}j_{l}(k_{\textsc{nl}}r)Y_{lm}(\theta,\phi),\hskip 2 8.452756ptn^{\text{out}}=0,\] (8a) \[\phi^{\text{in}} =\sum_{l,m}\left[D_{l}r^{l}-A_{l}\tfrac{e}{\varepsilon_{0} \varepsilon_{\infty}k_{\textsc{nl}}^{2}}j_{l}(k_{\textsc{nl}}r)\right]Y_{lm}( \theta,\phi),\] (8b) \[\phi^{\text{out}} =\sum_{l,m}\left[B_{l}r^{l}+C_{l}r^{-(l+1)}\right]Y_{lm}(\theta, \phi).\] (8c) Here, \(j_{l}\) and \(Y_{lm}\) are the spherical Bessel function of the first kind and the spherical harmonics, respectively. The current scalar potential \(\psi\) can be determined from Eq. (6c). We neglect variations in the exciting electric field and assume a constant electric field surrounding the sphere, here directed in the \(\mathbf{\hat{z}}\) direction i.e. \(\mathbf{E^{\text{out}}}=E_{0}\mathbf{\hat{z}}\). Thus, this poses the requirement that \(\lim_{r\to\infty}\phi^{\text{out}}=-E_{0}z=-E_{0}r\cos(\theta)\), which excludes all orders of \((l,m)\) in the sums in Eq. (8) except \((l,m)=(1,0)\). Applying the BCs from Eq. (7) and following the usual approach to introducing the polarizability [3], we determine the nonlocal polarizability \(\alpha_{\textsc{nl}}\) to be \[\alpha_{\textsc{nl}}=4\pi R^{3}\frac{\varepsilon_{\textsc{d}}- \varepsilon_{\textsc{b}}\left(1+\delta_{\textsc{nl}}\right)}{\varepsilon_{ \textsc{d}}+2\varepsilon_{\textsc{b}}\left(1+\delta_{\textsc{nl}}\right)}, \hskip 28.452756pt\delta_{\textsc{nl}}=\frac{\varepsilon_{\textsc{d}}- \varepsilon_{\infty}}{\varepsilon_{\infty}}\frac{j_{1}(k_{\textsc{nl}}R)}{k_{ \textsc{nl}}Rj_{1}^{\prime}(k_{\textsc{nl}}R)},\] (9) where the prime denotes differentiation with respect to the argument. We see that nonlocal effects enter the Clausius–Mossotti factor as an elegant and simple rescaling of either the metal permittivity from \(\varepsilon_{\textsc{d}}\) to \(\tilde{\varepsilon}_{\textsc{d}}=\varepsilon_{\textsc{d}}\left(1+\delta_{ \textsc{nl}}\right)^{-1}\) or of the background permittivity from \(\varepsilon_{\textsc{b}}\) to \(\tilde{\varepsilon}_{\textsc{b}}=\varepsilon_{\textsc{b}}(1+\delta_{\textsc{nl }})\). Both approaches are equally valid, but we choose to examine the rescaled background permittivity since the nonlocal blueshift of the SP resonance, which is discussed in the following, can be more easily understood in terms of a change in the background permittivity. We point out that the rescaled background permittivity \(\tilde{\varepsilon}_{\textsc{b}}\) is now both frequency- and size-dependent. Finally, we note that when \(\beta\to 0\) then \(\delta_{\textsc{nl}}\to 0\) in Eq. (9) and the classical size-independent Clausius–Mossotti factor is retrieved. With the nonlocal polarizability we can determine the extinction cross section \(\sigma_{\text{ext}}\) of a metal sphere using the relation [3] \[\sigma_{\text{ext}}=\frac{1}{\pi R^{2}}\left[\frac{(\omega/c)^{4} }{6\pi}|\alpha_{\textsc{nl}}|^{2}+(\omega/c)\text{Im}(\alpha_{\textsc{nl}}) \right].\] (10) [FIGURE:S3.F2][ENDFIGURE] In Fig. 2(a) we show the extinction cross section as a function of diameter and frequency for a model sphere in vacuum and with only a free-electron response. The blueshift of the SP resonance energy for decreasing particle diameter, which is known to be present from generalized nonlocal Mie theory [9], is captured accurately by the simple nonlocal Clausius–Mossotti factor in Eq. (9). Furthermore, we see that as the particle diameter increases the resonance energy approaches the well-known classical limit \(\omega/\omega_{\textsc{p}}=1/\sqrt{3}\approx 0.577\). For the smallest diameters (\(2R<5\) nm) a series of strongly size-dependent resonances above the plasma frequency can be distinguished. These are resonant pressure-type (longitudinal) waves that arise due to the confinement of the free electron gas. Comparison with the generalized Mie theory [9] (not displayed) shows that the spectral location and spectral width of the pressure resonances predicted by the nonlocal Clausius–Mossotti factor are exact. Using the nonlocal Clausius–Mossotti factor we can deduce a simple approximate, but accurate relation which determines the resonance frequencies of the pressure modes. The poles of the nonlocal correction \(\delta_{\textsc{nl}}\) in Eq. (9) determine the spectral position of the pressure modes, which provides us with the condition \(j_{1}^{\prime}(k_{\textsc{nl}}R)=0\). We rewrite this condition in terms of the standard Bessel functions and use the large-argument asymptotic form of the Bessel function \(J_{l}(x)\simeq\sqrt{2/(\pi z)}\cos(z-l\pi/2-\pi/4)\), since the product \(k_{\textsc{nl}}R\geq 1\) due to the high frequencies (\(\omega>\omega_{\textsc{p}}\)) at which these resonances occur. After some straightforward algebraic manipulations we find (for negligible damping) the relation \[\omega^{2}\simeq\frac{\omega_{\textsc{p}}^{2}}{\varepsilon_{ \infty}}+\frac{\beta^{2}\pi^{2}}{R^{2}}n^{2},\] (11) where formally \(n=1,2,3,..\). However, upon comparison with extinction cross section calculations we find that the mode \(n=1\) is optically dark and therefore does not show up in the extinction spectrum [41]. Figures 2(b-c) display the frequency dependency of the real and imaginary parts of the rescaled background permittivity \(\tilde{\varepsilon}_{\textsc{b}}(\omega,R)\), respectively, for three different radii. In Fig. 2(b) we see that below the plasma frequency \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) decreases from unity with decreasing radii, leading to the size-dependent blueshift observed in the extinction cross section. In the same frequency interval, we see from Fig. 2(c) that \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) does not vary significantly and is close to zero. Above the plasma frequency both \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) and \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) display periodic variations, which give rise to the pressure resonances in the extinction cross section. Finally, as the radius increases the frequency dependence of both \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) and \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) weakens, and the classical limits \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\to 1\) and \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\to 0\) are approached. The above derivation of the nonlocal polarizability \(\alpha_{\textsc{nl}}\) of a metal sphere in a homogeneous dielectric environment is expected to describe many experimental situations of spheres in glass or gels [22, 23, 42]. It can also be used, although its accuracy remains to be tested, in case an inhomogeneous environment is described with an effective homogeneous background dielectric function, see Sec. 4. ### Hydrodynamic sphere on substrate of finite thickness We consider next the case of a metal sphere situated on a substrate, as in the experiment, so we drop the assumption that the background is homogeneous. We present here an exact method based on scattering matrices and multipole expansions to calculate the extinction cross section of the sphere-substrate system, when impinged by a plane wave [43]. The dielectric constant and the thickness of the substrate are denoted \(\varepsilon_{\textsc{s}}\) and \(t\), respectively. Taking retardation effects into account, Mie’s scattering matrix for the metal sphere is \[\mbox{{T}}_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma}=t_{l}^{\sigma} \delta_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma},\] (12) where \(\sigma=1,2\) represent TE and TM polarizations, respectively; \(\delta_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma}=1\) if \(l=l^{\prime}\), \(m=m^{\prime}\), and \(\sigma=\sigma^{\prime}\), otherwise \(\delta_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma}=0\). The nonlocal Mie coefficients \(t_{l}^{\sigma}\) are given as \[t_{l}^{1} =-\frac{{{j_{l}}(x_{\textsc{d}})j_{l}^{\prime}(x_{\textsc{b}})-{j _{l}}(x_{\textsc{b}})j_{l}^{\prime}(x_{\textsc{d}})}}{{{j_{l}}(x_{\textsc{d}}) h_{l}^{(1)\prime}(x_{\textsc{b}})-h_{l}^{(1)}(x_{\textsc{b}})j_{l}^{\prime}(x_ {\textsc{d}})}},\] (13a) \[t_{l}^{2} =-\frac{\left[c_{l}+j_{l}^{\prime}(x_{\textsc{d}})\right] \varepsilon_{\textsc{b}}j_{l}(x_{\textsc{b}})-\varepsilon_{\textsc{d}}j_{l}(x_ {\textsc{d}})j_{l}^{\prime}(x_{\textsc{b}})}{\left[c_{l}+j_{l}^{\prime}(x_{ \textsc{d}})\right]\varepsilon_{\textsc{b}}h_{l}^{(1)}(x_{\textsc{b}})- \varepsilon_{\textsc{d}}j_{l}(x_{\textsc{d}})h_{l}^{(1)\prime}(x_{\textsc{b}})},\] (13b) where \[x_{\textsc{b}}=\omega\sqrt{\varepsilon_{\textsc{b}}}R/c\] and \[x_{\textsc{d}}=\omega\sqrt{\varepsilon_{\textsc{d}}}R/c\] . The nonlocal correction \[c_{l}\] to the Mie coefficients is given as \[c_{l}=l(l+1)\frac{j_{l}(x_{\textsc{nl}})j_{l}(x_{\textsc{d}})}{x_{\textsc{nl}} j_{l}^{\prime}(x_{\textsc{nl}})}\frac{\varepsilon_{\textsc{d}}-\varepsilon_{ \infty}}{\varepsilon_{\infty}},\] (13c) with \(x_{\textsc{nl}}=k_{\textsc{nl}}R\). We note that for \(l=1\) the nonlocal correction in Eq. (13c) has the same structural form as \(\delta_{\textsc{nl}}\) in the nonlocal Clausius–Mossotti factor, Eq. (9). In fact they are related as \(c_{1}=2j_{1}(x_{\textsc{d}})\delta_{\textsc{nl}}\). In the absence of the substrate, the matrix **T** connects the incident and scattered wave amplitudes **a** and **b**, respectively, through the relation \(\mbox{{b}}_{l^{\prime}m^{\prime}}^{\sigma^{\prime}}=\mbox{{T}}_{l^{\prime}m^{ \prime}\sigma^{\prime}}^{lm\sigma}\mbox{{a}}_{lm}^{\sigma}\). In the presence of the substrate, reflections from the substrate must be taken into account, which changes Mie’s scattering matrix **T** to the total scattering matrix **M** given as \[\mbox{{M}}=(\mbox{{I}}-\mbox{{T}}\mbox{{S}})^{-1}\mbox{{T}}.\] (14) The total scattering matrix **M** takes into account the interactions between the substrate and the sphere through the substrate scattering matrix **S**. The substrate matrix **S** can be derived by considering the reflections of the spherical waves by the substrate. In particular, **S** is given as \[\mbox{{S}}_{l^{\prime}m^{\prime}1}^{lm1} =s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y} }\frac{{f_{1}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(1)}+f_{2}}y_{lm}^{(2)}y_{ l^{\prime}-m^{\prime}}^{(2)}}{{k_{\textsc{b}z}}}},\] (15a) \[\mbox{{S}}_{l^{\prime}m^{\prime}2}^{lm2} =s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y} }\frac{{f_{2}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(1)}+f_{1}}y_{lm}^{(2)}y_{ l^{\prime}-m^{\prime}}^{(2)}}{{k_{\textsc{b}z}}}},\] (15b) \[\mbox{{S}}_{l^{\prime}m^{\prime}1}^{lm2} =-s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y }}\frac{{f_{2}}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(2)}+f_{1}y_{lm}^{(2)}y_ {l^{\prime}-m^{\prime}}^{(1)}}{{k_{\textsc{b}z}}}},\] (15c) \[\mbox{{S}}_{l^{\prime}m^{\prime}2}^{lm1} =-s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y }}\frac{f_{1}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(2)}+f_{2}y_{lm}^{(2)}y_{l ^{\prime}-m^{\prime}}^{(1)}}{{k_{\textsc{b}z}}}},\] (15d) with \[s_{ll^{\prime}}^{mm^{\prime}}=\frac{{2{i^{l^{\prime}-l}}{{(-1)}^ {l+m+m^{\prime}+1}}}}{{k_{\textsc{b}}\sqrt{l^{\prime}(l^{\prime}+1)}\sqrt{l(l+ 1)}}},\quad y_{lm}^{(1)}=\frac{\partial Y_{lm}(\Omega_{\mathbf{k}_{\textsc{b}} })}{\partial\theta_{\mathbf{k}_{\textsc{b}}}},\quad y_{lm}^{(2)}=\frac{mY_{lm} (\Omega_{\mathbf{k}_{\textsc{b}}})}{\sin\theta_{\mathbf{k}_{\textsc{b}}}},\] (16) where \(\mathbf{k}_{\textsc{b}}\) represents the wavevector of the plane wave in the background, \(k_{\textsc{b}z}\) is the \(z\) component of \(\mathbf{k}_{\textsc{b}}\) with the imaginary part being non-negative, \(\sin\theta_{\mathbf{k}_{\textsc{b}}}=\sqrt{k_{x}^{2}+k_{y}^{2}}/k_{\textsc{b}}\), and the integration ranges of \(k_{x}\) and \(k_{y}\) are both from \(-\infty\) to \(\infty\). The coefficients \(f_{\sigma}\) in Eq. (15) represent the reflection coefficients of the substrate for TE and TM polarized plane waves, respectively, which are expressed as \[f_{\sigma} =\frac{r_{\sigma}\left[1-\exp(ik_{\textsc{s}z}2t)\right]}{1-r_{ \sigma}^{2}\exp(ik_{\textsc{s}z}2t)}\exp(ik_{\textsc{b}z}2R),\] (17a) where \[k_{\textsc{s}z}\] represents the \[z\] component of the wavevector in the substrate. Furthermore, \[r_{\sigma}\] is the reflection coefficient between the background and the semi-infinite substrate given as \[r_{1}=\frac{k_{\textsc{b}z}-k_{\textsc{s}z}}{k_{\textsc{b}z}+k_{\textsc{s}z}}, \quad r_{2}=\frac{\varepsilon_{\textsc{s}}k_{\textsc{b}z}-\varepsilon_{\textsc {b}}k_{\textsc{s}z}}{\varepsilon_{\textsc{s}}k_{\textsc{b}z}+\varepsilon_{ \textsc{b}}k_{\textsc{s}z}}.\] (17b) With the total scattering matrix **M**, we can numerically compute the extinction cross section of the metal sphere on a substrate of finite thickness, using the relation \[\sigma_{\text{ext}}=-\frac{1}{k_{\textsc{b}}^{2}}\text{Re}( \mathbf{a}^{\text{T}}\mathbf{M}\mathbf{a}^{*}),\] (18) where superscripts T and * denote the transpose and complex conjugate, respectively. From the extinction cross section we determine the SP resonance energy. [FIGURE:S3.F3][ENDFIGURE] ## 4 Results In Fig. 3(a), we show the EELS measurements of the SP resonance energy \(E\) as a function of the particle diameter \(2R\). Two distinct features are present. The first is the spread of the resonance energy at a fixed particle diameter. In Ref. [1] we argue in detail that the spread is due to shape variations of the nanoparticle. Briefly, from the 2D STEM images we determine the area of the particle \(A\) and assign it a diameter, assuming a spherical shape \(\left(\text{i.e.}~{}A=\pi R^{2}\right)\). Different particles with slight deviations from spherical shape can lead to the same area and ultimately the same diameter. However, their SP resonance changes and this is what we observe experimentally. The important second feature we observe is a significant blueshift of the resonance energy of 0.5 eV as the particle diameter decreases. The blueshift is in good agreement with earlier results [24, 26, 27]. A classical local-response theory based on a size-independent dielectric function of the material does not predict any frequency shift at all. Figure 3(b) displays again the SP resonance energy \(E\), now as a function of the inverse particle diameter \(1/(2R)\). The experimental measurements suggest a linear relationship between the energy and inverse particle diameter. The nearly linear trend is also seen in the theoretical calculations based on the hydrodynamic model, shown with dashed and solid lines in Fig. 3(b), albeit with a smaller slope. We point out that the apparent \(1/(2R)\) dependent blueshift is only a first-order approximation in the hydrodynamic theory [1]. The dashed line in Fig. 3(b) corresponds to calculations of a hydrodynamic sphere embedded in a homogeneous environment, i.e. the nonlocal Clausius–Mossotti factor described in Sec. 3.1. The permittivity of the background dielectric is fitted to the average resonance of the largest particles (\(2R>20~{}\text{nm}\)) to ensure the correct classical SP resonance. We find \(\varepsilon_{\textsc{b}}=1.53\). The solid line shows the resonance energy determined from extinction cross section calculations of a hydrodynamic sphere in vacuum situated on a 10 nm thick Si\({}_{3}\)N\({}_{4}\) substrate, as described in Sec. 3.2. Here no fitting of the background permittivity is performed and we use \(\varepsilon_{\textsc{s}}=4.4\) as the permittivity of the substrate, suitable for Si\({}_{3}\)N\({}_{4}\)[44]. The same material parameters for the Ag sphere are used in both calculations [45]. While the substrate-based calculation shows an overall lower resonance energy for all particle sizes, both approaches show a linear tendency with a nearly identical slope. Compared to a free-space environment the presence of the dielectric substrate should induce a larger blueshift in the hydrodynamic model [1], and indeed it does (comparison not shown in Fig. 3). The fitted effective background permittivity in the calculations based on the nonlocal Clausius-Mossotti relation is larger than that of free space, and this makes that the two theoretical curves in Fig. 3(b) become almost parallel. Especially for the smallest particles \(\left[1/(2R)>0.1~{}\text{nm}^{-1}\right]\) the trend is striking similar, which indicates that (i) only the dipole mode of the sphere is important and (ii) the dipole mode is not significantly altered by the presence of the substrate. However, for larger particle diameters \(\left[1/(2R)<0.1~{}\text{nm}^{-1}\right]\) the substrate alters the dipole mode, which is visible in the slight convex curvature of the solid line in Fig. 3(b), in contrast to the concave curvature of the dashed line. Surprisingly higher order multipoles in the sphere, which are anticipated to be enhanced due to the presence of the substrate [46], show no significant contribution in the optical response. This is in fact due to the large interband absorption present in Ag at the resonance energies of the higher order multipoles, which heavily dampens the contribution from these modes. From Fig. 3(b) we see that the experimentally observed blueshift exceeds the theoretical blueshift predicted by the nonlocal Clausius–Mossotti factor. In Ref. [1] we conjectured that the presence of the substrate could induce the experimentally observed larger blueshift, but from Fig. 3(b) we see in more detail that the substrate-based calculations do not show a larger shift in energy than the nonlocal Clausius–Mossotti factor. ## 5 Conclusions We have studied the experimentally observed blueshift of the SP resonance energy of Ag nanoparticles, when the particle diameters decrease from 26 nm to 3.5 nm. To interpret the measurements we considered two different systems within the theory of the nonlocal hydrodynamic model: a metal sphere embedded in a homogeneous environment and a metal sphere situated on a dielectric substrate of finite thickness. Surprisingly, we find that both systems give rise to similar-sized blueshifts with decreasing particle size, despite the presence of the symmetry-breaking substrate. Both theoretical calculations are in qualitative agreement with the measurements, but the theoretically calculated blueshift is smaller than the blueshift observed in the EELS measurements. Thus, we conclude that the inclusion of the substrate in the theoretical calculations can not quantitatively explain the measurements. This leads us to believe that the deviation between theory and experiment are to be sought for in the intrinsic properties of silver, such as the spill-out of electrons in combination with the screening from the _d_ electrons [47, 48] and size-dependent changes in the electronic band structure [23], which are not taken into account in a hydrodynamic description. ## 6 Acknowledgements We thank Prof. U. Kreibig and Prof. A.-P. Jauho for stimulating discussions. We also acknowledge the help and collaboration from our co-authors in Ref. [1]. The Center for Nanostructured Graphene is sponsored by the Danish National Research Foundation, Project DNRF58. The A. P. Møller and Chastine Mc-Kinney Møller Foundation is gratefully acknowledged for the contribution toward the establishment of the Center for Electron Nanoscopy.

Пересчет смещения длин волн поверхностного плазмонного резонанса в серебряных наночастицах: влияние подложки Сорен Раза,\({}^{1,2}\) Вей Ян,\({}^{1,3}\) Николас Стенгер,\({}^{1,3}\) Мартейн Вубс,\({}^{1,3}\) и Н. Асгер Мортенсен\({}^{1,3,{\dagger}}\) ###### Аннотация Мы изучаем синее смещение энергии резонанса поверхностного плазмон-резонанса (СП) изолированных наночастиц серебра при уменьшении их диаметра, которое мы недавно измерили с помощью спектроскопии потерь энергии электронов (EELS) [1]. При уменьшении диаметра частицы от 26 до 3,5 нм наблюдается сильное синее смещение энергии резонанса СП на 0,5 эВ. В данной работе мы основываемся нашей теоретической интерпретации экспериментальных результатов на модели нелокальной гидродинамики и сравниваем влияние подложки на энергию резонанса СП с эффективной однородной фоновой проницаемостью. Мы получаем нелокальную поляризуемость маленькой металлической сферы, погруженной в однородную диэлектрическую среду, что позволяет обобщить классический фактор Клаузиуса-Моссотти с учетом нелокальности. Мы также представляем точную формализацию на основе многочленных разложений и рассеивающих матриц для определения оптического отклика металлической сферы на диэлектрическую подложку конечной толщины, с учетом затухания и нелокальных эффектов. Мы обнаруживаем, что расчеты на основе подложки показывают схожее по величине синее смещение, как расчеты на основе сферы в однородной среде, и что качественно согласуются с измерениями EELS. \({}^{1}\)Отделение инженерии фотоники, Технический университет Дании, DK-2800 Кгс. Люнгбю, Дания. \({}^{2}\)Центр электронной наноскопии, Технический университет Дании, DK-2800 Кгс. Люнгбю, Дания. \({}^{3}\)Центр наноструктурированного графена (CNG), Технический университет Дании, DK-2800 Кгс. Люнгбю, Дания. \({}^{\dagger}\)[email protected] - \({}^{\dagger}\)[email protected] (240.6680) Поверхностные плазмоны. (250.5403) Плазмоника. (160.4236) Наноматериалы. (000.1600) Классическая и квантовая физика. (260.3910) Оптика металлов. ## Ссылки * [1] С. Раза, Н. Стенгер, С. Кадходазадех, С. В. Фишер, Н. Костеша, А.-П. Яухо, А. Берроус, М. Вубс и Н. А. Мортенсен, «Синее смещение резонанса поверхностного плазмона в серебряных наночастицах, изученное с помощью EELS», Nanophotonics 2, 131-138 (2013). * [2] Г. Ми, «Вклады в оптику таких сред, как коллоидные металлические растворы», Ann. Phys. 330, 377-445 (1908). * [3] С. А. Майер, "Плазмоника: основы и применение" (Спрингер, Нью-Йорк, 2007). * [4] Н. Д. Ланг и У. Кон, "Теория металлических поверхностей: плотность заряда и поверхностная энергия", Физ. Rev. B 1, 4555-4568 (1970). * [5] А. Бордман, Б. Паранжапе и Р. Тешима, «Влияние структуры на поверхностные плазмоны», Surf. Sci. 49, 275-292 (1975). * [6] А. Дж. Беннет, "Влияние распределения заряда электрона на дисперсию поверхностных плазмонов", Phys. Rev. B 1, 203-207 (1970). * [7] P. Apell, "Простая выводов поверхностного вклада к отражательной способности металла и его использование в ван-дер-ваальсовском взаимодействии", Phys. Scr. 24, 795 (1981). * [8] P. J. Фейбельман, "Поверхностные электромагнитные поля", Prog. Surf. Sci. 12, 287-407 (1982). * [9] Р. Руппин, "Оптические свойства плазменной сферы", Phys. Rev. Lett. 31, 1434-1437 (1973). * [10] А. Д. Бордмен и Б. В. Паранджапе, "Оптические поверхностные моды металлических сфер", J. Phys. F: Met. Phys. 7, 1935 (1977). * [11] P. Apell и Å. Ljungbert, "Общая нелокальная теория электромагнитного отклика малой металлической частицы", Phys. Scr. 26, 113 (1982). * [12] C. Schwartz и W. L. Schaich, "Гидродинамические модели поверхностных плазмонов", Phys. Rev. B 26, 7008-7011 (1982). * [13] A. I. Fernández-Domínguez, A. Wiener, F. J. García-Vidal, S. A. Maier и J. B. Pendry, "Описание оптических переходов в плазмонных наноструктурах с использованием оптики превращения", Phys. Rev. Lett. 108, 106802 (2012). * [14] C. Девид и Ф. Ж. Гарсия де Абахо, "Пространственная нелокальность в оптическом отклике металлических наночастиц", J. Phys. Chem. C 115, 19470-19475 (2012). * [15] G. Toscano, S. Raza, A.-П. Jauho, N. A. Mortensen и M. Wubs, "Измененное усиление и поглощение в плазмонных нанопроводах из-за нелокального отклика", Opt. Express 20, 4176-4188 (2012). * [16] C. Ciracì, R. T. Hill, J. J. Mock, Y. Urzhumov, A. I. Fernández-Domínguez, S. A. Maier, J. B. Pendry, A. Chilkoti и D. R. Smith, “Исследование пределов усиления плазмонов”, Science 337, 1072-1074 (2012). * [17] U. Kreibig и C. Fragstein, "Ограничение среднего свободного пробега электронов в малых серебряных частицах", Z. Physik 224, 307-323 (1969). * [18] L. Genzel, Т. Мартин и U. Kreibig, "Диэлектрическая функция и плазменный резонанс малых металлических частиц", Z. Phys. B 21, 339-346 (1975). * [19] P. Apell и ## 1 Введение Использование металлических наночастиц для создания удивительных цветов в витраже уходит своими корнями в древнеримские времена. Однако, механизм порождения цвета не был полностью понятен до тех пор, пока в 1908 году Ми строго и точно не решил электродинамические уравнения Максвелла для задачи о рассеянии плоской волны на сфере [2]. Из решения Ми следует, что резонансные моды металлической сферы, которые мы сейчас называем локализованными поверхностными плазмонами [3], приводят к большим поперечным сечениям поглощения при определенных длинах волн, что и вызывает яркие цвета в витраже. В обработке задачи Ми предполагается, что свойства материала сферы можно описать единственной зависящей от частоты функцией - локальной диэлектрической функцией \(\varepsilon(\omega)\). В большинстве случаев классическое рассмотрение на основе диэлектрической функции оправдано, однако важные эффекты, связанные с поверхностной структурой [4, 5, 6, 7, 8], нелокальным ответом [9, 10, 11, 12, 13, 14, 15, 16] и квантовыми размерными эффектами [17, 18, 19, 20], проявляются в ответе металлических наночастиц, когда размеры частиц меньше \(\sim 10\) нм. Множество экспериментов на малых наночастицах, используя как оптические измерения [21, 22, 23, 24, 25], так и исследования потерь энергии электрона [26, 27, 1], показали, что классический подход недостаточен для описания экспериментальных наблюдений. Интерпретация этих результатов была основана на полу-классических моделях, таких как нелокальный гидродинамический [28] и полу-классический метод с бесконечным барьером (SCIB) [29], или более сложных квантовых расчетах с использованием функционала плотности [4]. Недавно мы провели EELS на химически синтезированных серебряных наночастицах с диаметрами от 3,5 до 26 нм [1]. Мы наблюдали большое смещение в сторону увеличения энергии локализованных SP-резонансов с 3,2 эВ до 3,7 эВ при уменьшении размера частиц. Мы интерпретировали эти не-классические наблюдения, используя две различные полу-классические модели - гидродинамическую модель и модель, представленную Keller et al. [20], которые обе могут только качественно объяснить наблюдения. В этой статье мы фокусируемся на гидродинамической модели и находим нелокальную поляризуемость гидродинамической сферы в однородной среде, что приводит к нелокальной обобщенной фактору Клаузиуса-Моссотти. Мы также исследуем влияние подложки на энергию резонанса наночастицы. Конкретно, мы разрабатываем точную формализацию для расчета оптического отклика металлической сферы на диэлектрическую подложку конечной толщины, учитывая задержку и нелокальный отклик. Теоретические расчеты сравниваются с измерениями EELS. ## 2 Эксперимент: спектроскопия потери энергии электрона Серебряные наночастицы искусственно синтезируются [30] и затем стабилизируются в водном растворе с ионами борогидрида для предотвращения их агрегации. После этого раствор с наночастицами наносится на плазмой очищенную ТЭМ-мембрану из кремниевого нитрида (толщиной 10 нм), приобретенную на TEMwindows.com. Средний диаметр частиц составляет 12 нм с широким распределением размеров от 2 нм до 30 нм, см. Рис. 1, что позволяет нам проводить все измерения на одном и том же образце. Измерения EELS выполняются с помощью трансмиссионного электронного микроскопа FEI Titan, оснащенного монохроматором и корректором аберраций зонда. Микроскоп работает в режиме сканирующего электронного микроскопа (STEM) при напряжении ускорения 120 кВ, обеспечивая диаметр зонда 0,5 нм и ширину пика нулевой потери \(0,15\pm0,05\) эВ. Для усиления возбуждения SP спектры EELS получаются путем направления электронного зонда на поверхность серебряной наночастицы (траектория aloof). Подробности анализа данных и дополнительной экспериментальной информации можно найти в работе [1]. [FIGURE:S2.F1][ENDFIGURE] ## Теория: гидродинамическая модель В следующих теоретических подходах мы будем предполагать, что форма наночастиц может быть приближена к сферической. Детали и обсуждение этого приближения можно найти в работе [1]. Здесь мы отмечаем на основе изображений в ТЭМ на рис. 1(б-ф), что общая форма наночастиц сферическая, особенно для размеров частиц менее 10 нм в диаметре, что подтверждает наше приближение. Мы основываем интерпретацию наших экспериментальных результатов на гидродинамической модели. В первую очередь, мы находим точную нелокальную поляризуемость металлической сферы в однородной среде, обобщая известный фактор Клаузиуса-Моссотти на нелокальный отклик. Свободные электроны сферы описываются полуклассической гидродинамической моделью, которая учитывает нелокальный отклик, но пренебрегает выходом электронов за пределы сферы из-за конечности связывающего их потенциала. Во-вторых, учитывается влияние подложки. Здесь мы представляем точную формализацию для расчета замедленного оптического отклика сферы с гидродинамическим нелокальным откликом на диэлектрической подложке конечной толщины. Начальной точкой гидродинамической модели являются уравнения Максвелла в терминах плотности свободных электронов \(n\) и свободного электронного тока \(\mathbf{J}\)[28, 31, 32] \[ \mathbf{\nabla}\cdot\mathbf{D} =-en, \quad (1a) \] \[ \mathbf{\nabla}\cdot\mathbf{H} =0, \quad (1b) \] \[ \mathbf{\nabla}\times\mathbf{E} =i\omega\mu_{0}\mathbf{H}, \quad (1c) \] \[ \mathbf{\nabla}\times\mathbf{H} =-i\omega\mathbf{D}+\mathbf{J}, \quad (1d) \] где использовано конститутивное соотношение \(\mathbf{B}=\mu_{0}\mathbf{H}\) для неимеющих магнитных материалов. Здесь мы вводим эффекты поляризации, вызванные связанными зарядами, через конститутивное соотношение для поля смещения \(\mathbf{D}=\varepsilon_{0}\varepsilon_{\infty}\mathbf{E}\), где \(\varepsilon_{\infty}\) обычно зависит от частоты и учитывает эффекты поляризации, не связанные с свободными электронами, такие как межзонные переходы. Уравнение непрерывности, связывающее плотность свободных электронов и свободный электронный ток, непосредственно следует из уравнений (1a) и (1d), \[\mathbf{\nabla}\cdot\mathbf{J}=-i\omega en.\] (2) \[\mathbf{\nabla}\cdot\mathbf{J}=-i\omega en.\] (2) Для завершения описания электромагнитного отклика металла требуется связь, которая связывает свободный электронный ток с электрическим полем. В этой связи мы рассматриваем линеаризованное нелокальное гидродинамическое уравнение [28, 33], которое в своей формулировке в реальном пространстве становится [15, 34, 35]. \[\frac{\beta^{2}}{\omega(\omega+i\gamma)}\mathbf{\nabla}\left( \mathbf{\nabla}\cdot\mathbf{J}\right)+\mathbf{J}=\varepsilon_{0}\sigma\mathbf{ E},\] (3) \[\frac{\beta^{2}}{\omega(\omega+i\gamma)}\mathbf{\nabla}\left( \mathbf{\nabla}\cdot\mathbf{J}\right)+\mathbf{J}=\varepsilon_{0}\sigma\mathbf{ E},\] (3) где \(\sigma=i\omega_{\textsc{p}}^{2}/(\omega+i\gamma)\) - классическая проводимость Друде, а \(\beta^{2}=3/5v_{\textsc{f}}^{2}\) , где \(v_{\textsc{f}}\) - скорость Ферми. В рамках гидродинамического описания включено давление электронного газа, что приводит к появлению продольных волн и пространственному рассеянию, которое наблюдается в действительных наноплазмонических системах. Уравнения (1-3) составляют основной набор уравнений в рамках задержанного гидродинамического подхода. На границе между двумя материалами эти уравнения дополняются граничными условиями. В данном исследовании мы рассматриваем только металлические-диэлектрические границы, где граничные условия Максвелла должны быть дополнены одним дополнительным граничным условием, которое гласит, что нормальная составляющая плотности свободных электронных токов должна обращаться в нуль [31, 34, 36, 37, 38]. Это дополнительное граничное условие может быть получено в результате пренебрежения вытеканием электронов. ### Гидродинамическая сфера в однородной среде: нелокальный фактор Клаузиуса-Моссотти Мы рассматриваем малую изотропную металлическую сферу радиусом \(R\), вложенную в однородную диэлектрическую среду с относительной диэлектрической проницаемостью \(\varepsilon_{\textsc{b}}\). Поляризуемость \(\alpha\) этой сферы - известный результат в классической оптике [3, 39] и задается уравнением \[\alpha=4\pi R^{3}\frac{\varepsilon_{\textsc{d}}-\varepsilon_{ \textsc{b}}}{\varepsilon_{\textsc{d}}+2\varepsilon_{\textsc{b}}},\] (4) \[\alpha=4\pi R^{3}\frac{\varepsilon_{\textsc{д}}-\varepsilon_{ \textsc{б}}}{\varepsilon_{\textsc{д}}+2\varepsilon_{\textsc{б}}},\] (4) где \(\varepsilon_{\textsc{d}}=\varepsilon_{\infty}-\omega_{\textsc{p}}^{2}/(\omega^ {2}+i\gamma\omega)\) является классической друдовской диэлектрической проницаемостью. Фактор \((\varepsilon_{\textsc{d}}-\varepsilon_{\textsc{b}})/(\varepsilon_{\textsc{d}}+ 2\varepsilon_{\textsc{b}})\) называется фактором Клаузиуса-Моссотти, и обратите внимание, что он не зависит от радиуса сферы. Поляризуемость получена в квазистатическом приближении при предположении статического окружающего электрического поля и, следовательно, пренебрегает пространственными изменениями возбуждающего электрического поля. Нашей целью теперь является обобщение этой формулы с учетом гидродинамической нелокальной реакции сферы. Мы начинаем с введения электрического и тока скалярного потенциалов \(\phi\) и \(\psi\) соответственно, которые определены как \[ \mathbf{E}=-\mathbf{\nabla}\phi,\hskip 28.452756pt\mathbf{J}=- \mathbf{\nabla}\psi.\] (5) \[\mathbf{E}=-\mathbf{\nabla}\phi,\hskip 28.452756pt\mathbf{J}=- \mathbf{\nabla}\psi.\] (5) Подставив уравнение (5) в гидродинамические уравнения (1-3), можно легко показать, что скалярные потенциалы внутри металлической сферы определяются уравнениями [40] \[ \left(\nabla^{2}+k_{\textsc{nl}}^{2}\right)n=0, \quad (6a) \] \[ \nabla^{2}\phi=\tfrac{e}{\varepsilon_{0}\varepsilon_{\infty}}n, \quad (6b) \] \[ \psi=\tfrac{1}{i\omega-\gamma}\left(\varepsilon_{0}\omega_{\textsc{p}}^{2}\phi-e\beta^{2}n\right), \quad (6c) \] где нелокальный продольный волновой вектор задается как \(k_{\textsc{nl}}^{2}=(\omega^{2}+i\omega\gamma-\omega_{\textsc{p}}^{2}/ \varepsilon_{\infty})/\beta^{2}\). В окружающем диэлектрике плотность тока \(\mathbf{J}\) и плотность электронов \(n\) обращаются в ноль, и электрический скалярный потенциал должен удовлетворять обычному уравнению Лапласа \(\nabla^{2}\phi=0\). Наконец, Граничные условия Максвелла и гидродинамические граничные условия для скалярных потенциалов переводятся в \[\phi^{\text{in}}=\phi^{\text{out}},\hskip 28.452756pt\varepsilon_ {\infty}\frac{\partial\phi^{\text{in}}}{\partial r}=\varepsilon_{\textsc{b}} \frac{\partial\phi^{\text{out}}}{\partial r},\hskip 28.452756pt\frac{\partial \psi^{\text{in}}}{\partial r}=0,\] (7) \[\phi^{\text{вн}}=\phi^{\text{вых}},\hskip 28.452756pt\varepsilon_ {\infty}\frac{\partial\phi^{\text{вн}}}{\partial r}=\varepsilon_{\textsc{б}} \frac{\partial\phi^{\text{вых}}}{\partial r},\hskip 28.452756pt\frac{\partial \psi^{\text{вн}}}{\partial r}=0,\] (7) где _в_ и _наружу_ относятся кнутри и снаружи металла соответственно. Общие решения для электрического скалярного потенциала и плотности свободных электронов внутри и снаружи сферы - \[n^{\text{внутр}} =\sum_{l,m}A_{l}j_{l}(k_{\textsc{внеш}}r)Y_{lm}(\theta,\phi),\hskip 2 8.452756ptn^{\text{вне}}=0,\] (8а) \[\phi^{\text{внутр}} =\sum_{l,m}\left[D_{l}r^{l}-A_{l}\tfrac{e}{\varepsilon_{0} \varepsilon_{\infty}k_{\textsc{внеш}}^{2}}j_{l}(k_{\textsc{внеш}}r)\right]Y_{lm}( \theta,\phi),\] (8б) \[\phi^{\text{вне}} =\sum_{l,m}\left[B_{l}r^{l}+C_{l}r^{-(l+1)}\right]Y_{lm}(\theta, \phi).\] (8с) Здесь \(j_{l}\) и \(Y_{lm}\) являются сферическими функциями Бесселя первого рода и сферическими гармониками соответственно. Скалярный потенциал электрического тока \(\psi\) можно определить из уравнения (6c). Мы пренебрегаем изменениями побуждающего электрического поля и предполагаем постоянное электрическое поле, окружающее сферу, направленное вдоль оси \(\mathbf{\hat{z}}\), то есть \(\mathbf{E^{\text{out}}}=E_{0}\mathbf{\hat{z}}\). Таким образом, это требует, чтобы \(\lim_{r\to\infty}\phi^{\text{out}}=-E_{0}z=-E_{0}r\cos(\theta)\), что исключает все значения \((l,m)\) в суммах в уравнении (8), кроме \((l,m)=(1,0)\). Применяя граничные условия из уравнения (7) и следуя обычному подходу к введению поляризуемости [3], мы определяем нелокальную поляризуемость \(\alpha_{\textsc{nl}}\) как \[\alpha_{\textsc{nl}}=4\pi R^{3}\frac{\varepsilon_{\textsc{d}}- \varepsilon_{\textsc{b}}\left(1+\delta_{\textsc{nl}}\right)}{\varepsilon_{ \textsc{d}}+2\varepsilon_{\textsc{b}}\left(1+\delta_{\textsc{nl}}\right)}, \hskip 28.452756pt\delta_{\textsc{nl}}=\frac{\varepsilon_{\textsc{d}}- \varepsilon_{\infty}}{\varepsilon_{\infty}}\frac{j_{1}(k_{\textsc{nl}}R)}{k_{ \textsc{nl}}Rj_{1}^{\prime}(k_{\textsc{nl}}R)},\] (9) где примечание обозначает дифференциацию по аргументу. Мы видим, что нелокальные эффекты входят в фактор Клаузиуса-Моссотти как элегантное и простое изменение масштабирования металлической диэлектрической проницаемости с \(\varepsilon_{\textsc{d}}\) до \(\tilde{\varepsilon}_{\textsc{d}}=\varepsilon_{\textsc{d}}\left(1+\delta_{ \textsc{nl}}\right)^{-1}\) или фоновой диэлектрической проницаемости с \(\varepsilon_{\textsc{b}}\) до \(\tilde{\varepsilon}_{\textsc{b}}=\varepsilon_{\textsc{b}}(1+\delta_{\textsc{nl }})\). Оба подхода равноценны, но мы выбираем исследовать измененную фоновую диэлектрическую проницаемость, поскольку нелокальное смещение СП-резонанса, которое обсуждается далее, может быть лучше понято в терминах изменения фоновой диэлектрической проницаемости. Мы отмечаем, что измененная масштабированная фоновая диэлектрическая проницаемость \(\tilde{\varepsilon}_{\textsc{b}}\) теперь зависит как от частоты, так и от размера. Наконец, мы отмечаем, что когда \(\beta\to 0\), тогда \(\delta_{\textsc{nl}}\to 0\) в уравнении (9) и восстанавливается классический, не зависящий от размера, фактор Клаузиуса-Моссотти. С помощью нелокальной поляризуемости мы можем определить поглощающее поперечное сечение \(\sigma_{\text{ext}}\) металлической сферы с использованием соотношения [3]. \[\sigma_{\text{ext}}=\frac{1}{\pi R^{2}}\left[\frac{(\omega/c)^{4} }{6\pi}|\alpha_{\textsc{nl}}|^{2}+(\omega/c)\text{Im}(\alpha_{\textsc{nl}}) \right].\] (10) [FIGURE:S3.F2][ENDFIGURE] - [ФИГУРА:S3.F2][КОНЕЦФИГУРЫ] На рис. 2(a) показано сечение поглощения в зависимости от диаметра и частоты для модельной сферы в вакууме и только с ответом свободных электронов. Синее смещение энергии резонанса поверхностных плазмонов при уменьшении диаметра частицы, которое известно из обобщенной нелокальной теории Ми [9], точно воспроизводится простым нелокальным фактором Клаузиуса-Моссотти в формуле (9). Кроме того, мы видим, что с увеличением диаметра частицы энергия резонанса приближается к известному классическому пределу \(\omega/\omega_{\textsc{p}}=1/\sqrt{3}\approx 0.577\). Для самых маленьких диаметров (\(2R<5\) нм) можно выделить серию сильно зависящих от размера резонансов выше плазменной частоты. Это резонирующие волны давления (продольные), возникающие из-за ограничения свободного электронного газа. Сравнение с обобщенной теорией Ми [9] (не показана) показывает, что спектральное положение и спектральная ширина давительных резонансов, предсказанных нелокальным фактором Клаузиуса-Моссотти, точны. С использованием нелокального фактора Клаузиуса-Моссотти мы можем вывести простое приближенное, но точное соотношение, которое определяет резонансные частоты давлений. Полюса нелокальной поправки \(\delta_{\textsc{nl}}\) в уравнении (9) определяют спектральное положение давлений, что дает нам условие \(j_{1}^{\prime}(k_{\textsc{nl}}R)=0\). Мы перепишем это условие в терминах стандартных функций Бесселя и использовать асимптотическую форму функции Бесселя \(J_{l}(x)\simeq\sqrt{2/(\pi z)}\cos(z-l\pi/2-\pi/4)\), так как произведение \(k_{\textsc{nl}}R\geq 1\) из-за высоких частот (\(\omega>\omega_{\textsc{p}}\)), на которых происходят эти резонансы. После несложных алгебраических преобразований мы находим (для незначительного затухания) соотношение \[\omega^{2}\simeq\frac{\omega_{\textsc{p}}^{2}}{\varepsilon_{ \infty}}+\frac{\beta^{2}\pi^{2}}{R^{2}}n^{2},\] (11) где формально \(n=1,2,3,..\). Однако, сравнивая с расчетами сечения поглощения, мы обнаруживаем, что режим \(n=1\) является оптически темным и поэтому не отображается в спектре поглощения [41]. Фигуры 2(b-c) показывают зависимость от частоты действительной и мнимой частей масштабированной фоновой диэлектрической проницаемости \(\tilde{\varepsilon}_{\textsc{b}}(\omega,R)\) для трех разных радиусов. На рис. 2(b) мы видим, что ниже плазменной частоты \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) уменьшается от единицы с уменьшением радиуса, что приводит к зависимому от размера сдвигу в сторону синего цвета, наблюдаемому в сечении поглощения. В том же диапазоне частот мы видим на рис. 2(c), что \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) изменяется незначительно и близка к нулю. Выше плазменной частоты и \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) и \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) имеют периодические изменения, которые вызывают резонансы давления в сечении поглощения. Наконец, с увеличением радиуса частотная зависимость как \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\), так и \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\) ослабевает, и приближаются классические пределы \(\text{Re}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\to 1\) и \(\text{Im}(\tilde{\varepsilon}_{\textsc{b}})/\varepsilon_{\textsc{b}}\to 0\). Приведенное выше вывод нелокальной поляризуемости \(\alpha_{\textsc{nl}}\) металлической сферы в однородной диэлектрической среде ожидается, что оно описывает множество экспериментальных ситуаций сфер в стекле или гелях [22, 23, 42]. Также его можно использовать, хотя его точность еще предстоит проверить, в случае, когда неоднородная среда описывается эффективной однородной задней диэлектрической функцией, см. секцию 4. ### Гидродинамическая сфера на подложке конечной толщины Мы рассматриваем случай металлической сферы, расположенной на подложке, как в эксперименте, поэтому отбрасываем предположение о однородности фона. Мы представляем здесь точный метод на основе матриц рассеяния и мультипольных разложений для расчета поперечного сечения поглощения системы сфера-подложка при падении плоской волны [43]. Диэлектрическая постоянная и толщина подложки обозначаются \(\varepsilon_{\textsc{с}}\) и \(t\) соответственно. Учитывая ретардационные эффекты, рассеивающая матрица Ми для металлической сферы имеет вид \[ \mbox{{T}}_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma}=t_{l}^{\sigma} \delta_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma},\] (12) где \(\sigma=1,2\) представляют TE и TM поляризации соответственно; \(\delta_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma}=1\), если \(l=l^{\prime}\), \(m=m^{\prime}\) и \(\sigma=\sigma^{\prime}\), в противном случае \(\delta_{l^{\prime}m^{\prime}\sigma^{\prime}}^{lm\sigma}=0\). Нелокальные коэффициенты Ми \(t_{l}^{\sigma}\) задаются следующим образом \[t_{l}^{1} =-\frac{{{j_{l}}(x_{\textsc{d}})j_{l}^{\prime}(x_{\textsc{b}})-{j _{l}}(x_{\textsc{b}})j_{l}^{\prime}(x_{\textsc{d}})}}{{{j_{l}}(x_{\textsc{d}}) h_{l}^{(1)\prime}(x_{\textsc{b}})-h_{l}^{(1)}(x_{\textsc{b}})j_{l}^{\prime}(x_ {\textsc{d}})}},\] (13a) \[t_{l}^{2} =-\frac{\left[c_{l}+j_{l}^{\prime}(x_{\textsc{d}})\right] \varepsilon_{\textsc{b}}j_{l}(x_{\textsc{b}})-\varepsilon_{\textsc{d}}j_{l}(x_ {\textsc{d}})j_{l}^{\prime}(x_{\textsc{b}})}{\left[c_{l}+j_{l}^{\prime}(x_{ \textsc{d}})\right]\varepsilon_{\textsc{b}}h_{l}^{(1)}(x_{\textsc{b}})- \varepsilon_{\textsc{d}}j_{l}(x_{\textsc{d}})h_{l}^{(1)\prime}(x_{\textsc{b}})},\] (13b) где \[x_{\textsc{b}}=\omega\sqrt{\varepsilon_{\textsc{b}}}R/c\] и \[x_{\textsc{d}}=\omega\sqrt{\varepsilon_{\textsc{d}}}R/c\] . Исправка на нелокальность \[c_{l}\] к коэффициентам Ми задается как \[c_{l}=l(l+1)\frac{j_{l}(x_{\textsc{nl}})j_{l}(x_{\textsc{d}})}{x_{\textsc{nl}} j_{l}^{\prime}(x_{\textsc{nl}})}\frac{\varepsilon_{\textsc{d}}-\varepsilon_{ \infty}}{\varepsilon_{\infty}},\] (13c) с \(x_{\textsc{nl}}=k_{\textsc{nl}}R\). Заметим, что при \(l=1\) поправка к уравнению (13c) имеет такую же структурную форму, как и \(\delta_{\textsc{nl}}\) в нелинейном факторе Клаузиуса-Моссотти, уравнение (9). Фактически, они связаны как \(c_{1}=2j_{1}(x_{\textsc{d}})\delta_{\textsc{nl}}\). При отсутствии субстрата матрица **T** связывает амплитуды падающей и рассеянной волн **a** и **b** соответственно, через отношение \(\mbox{{b}}_{l^{\prime}m^{\prime}}^{\sigma^{\prime}}=\mbox{{T}}_{l^{\prime}m^{ \prime}\sigma^{\prime}}^{lm\sigma}\mbox{{a}}_{lm}^{\sigma}\). При наличии субстрата необходимо учитывать отражения от субстрата, что изменяет матрицу рассеяния Ми **T** на полную матрицу рассеяния **M**, заданную как \[\mbox{{M}}=(\mbox{{I}}-\mbox{{T}}\mbox{{S}})^{-1}\mbox{{T}}.\] (14) Полная матрица рассеяния **M** учитывает взаимодействие между подложкой и сферой через матрицу рассеяния подложки **S**. Матрица **S** подложки может быть получена путем рассмотрения отражений сферических волн подложкой. В частности, **S** задается следующим образом: \[ \mbox{С}_{l^{\prime}m^{\prime}1}^{lm1} =s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y}} \frac{{f_{1}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(1)}+f_{2}}y_{lm}^{(2)}y_{ l^{\prime}-m^{\prime}}^{(2)}}{{k_{\textsc{b}z}}}}, \] (15а) \[ \mbox{С}_{l^{\prime}m^{\prime}2}^{lm2} =s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y}} \frac{{f_{2}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(1)}+f_{1}}y_{lm}^{(2)}y_{ l^{\prime}-m^{\prime}}^{(2)}}{{k_{\textsc{b}z}}}}, \] (15б) \[ \mbox{С}_{l^{\prime}m^{\prime}1}^{lm2} =-s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y }}\frac{{f_{2}}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(2)}+f_{1}y_{lm}^{(2)}y_ {l^{\prime}-m^{\prime}}^{(1)}}{{k_{\textsc{b}z}}}}, \] (15с) \[ \mbox{С}_{l^{\prime}m^{\prime}2}^{lm1} =-s_{ll^{\prime}}^{mm^{\prime}}\iint{\text{d}{k_{x}}\text{d}{k_{y }}\frac{f_{1}y_{lm}^{(1)}y_{l^{\prime}-m^{\prime}}^{(2)}+f_{2}y_{lm}^{(2)}y_{l ^{\prime}-m^{\prime}}^{(1)}}{{k_{\textsc{b}z}}}}, \] (15d) с \[ s_{ll^{\prime}}^{mm^{\prime}}=\frac{{2{i^{l^{\prime}-l}}{{(-1)}^ {l+m+m^{\prime}+1}}}}{{k_{\textsc{b}}\sqrt{l^{\prime}(l^{\prime}+1)}\sqrt{l(l+ 1)}}},\quad y_{lm}^{(1)}=\frac{\partial Y_{lm}(\Omega_{\mathbf{k}_{\textsc{b}} })}{\partial\theta_{\mathbf{k}_{\textsc{b}}}},\quad y_{lm}^{(2)}=\frac{mY_{lm} (\Omega_{\mathbf{k}_{\textsc{b}}})}{\sin\theta_{\mathbf{k}_{\textsc{b}}}},\] (16) \] \[s_{ll^{\prime}}^{mm^{\prime}}=\frac{{2{i^{l^{\prime}-l}}{{(-1)}^ {l+m+m^{\prime}+1}}}}{{k_{\textsc{b}}\sqrt{l^{\prime}(l^{\prime}+1)}\sqrt{l(l+ 1)}}},\quad y_{lm}^{(1)}=\frac{\partial Y_{lm}(\Omega_{\mathbf{k}_{\textsc{b}} })}{\partial\theta_{\mathbf{k}_{\textsc{b}}}},\quad y_{lm}^{(2)}=\frac{mY_{lm} (\Omega_{\mathbf{k}_{\textsc{b}}})}{\sin\theta_{\mathbf{k}_{\textsc{b}}}},\] (16) где \(\mathbf{k}_{\textsc{b}}\) представляет волновой вектор плоской волны в фоне, \(k_{\textsc{b}z}\) является компонентой \(z\) вектора \(\mathbf{k}_{\textsc{b}}\) с неотрицательной мнимой частью, \(\sin\theta_{\mathbf{k}_{\textsc{b}}}=\sqrt{k_{x}^{2}+k_{y}^{2}}/k_{\textsc{b}}\), а интегральные диапазоны \(k_{x}\) и \(k_{y}\) оба от \(-\infty\) до \(\infty\). Коэффициенты \(f_{\sigma}\) в уравнении (15) представляют коэффициенты отражения подложки для TE и TM поляризованных плоских волн, соответственно, которые выражаются как \[f_{\sigma} =\frac{r_{\sigma}\left[1-\exp(ik_{\textsc{s}z}2t)\right]}{1-r_{ \sigma}^{2}\exp(ik_{\textsc{s}z}2t)}\exp(ik_{\textsc{b}z}2R),\] (17a) где \[k_{\textsc{s}z}\] представляет собой \[z\] компоненту волнового вектора в подложке. Кроме того, \[r_{\sigma}\] является коэффициентом отражения между фоном и полубесконечной подложкой, заданным следующим образом: \[r_{1}=\frac{k_{\textsc{b}z}-k_{\textsc{s}z}}{k_{\textsc{b}z}+k_{\textsc{s}z}}, \quad r_{2}=\frac{\varepsilon_{\textsc{s}}k_{\textsc{b}z}-\varepsilon_{\textsc {b}}k_{\textsc{s}z}}{\varepsilon_{\textsc{s}}k_{\textsc{b}z}+\varepsilon_{ \textsc{b}}k_{\textsc{s}z}}.\] (17b) С помощью полного рассеивающего матрицы **M** мы можем численно вычислить коэффициент поглощения металлической сферы на подложке конечной толщины, используя соотношение \[\sigma_{\text{ext}}=-\frac{1}{k_{\textsc{b}}^{2}}\text{Re}( \mathbf{a}^{\text{T}}\mathbf{M}\mathbf{a}^{*}),\] (18) \[\sigma_{\text{ext}}=-\frac{1}{k_{\textsc{b}}^{2}}\text{Re}( \mathbf{a}^{\text{T}}\mathbf{M}\mathbf{a}^{*}),\] (18) где верхние индексы T и * обозначают транспонирование и комплексное сопряжение соответственно. Из сечения поглощения мы определяем энергию резонанса SP. [FIGURE:S3.F3][ENDFIGURE] [ФИГУРА:S3.F3][КОНЕЦФИГУРЫ] ## 4 Результата На рис. 3(a) показаны измерения спектроскопии электронного рассеяния с низкой потерей (EELS) энергии резонанса SP \(E\) в зависимости от диаметра частицы \(2R\). Наблюдаются две отличительные особенности. Во-первых, это разброс энергии резонанса при фиксированном диаметре частицы. В [1] мы подробно объясняем, что этот разброс вызван вариациями формы наночастицы. Кратко говоря, изображения в режиме сканирующей трансмиссионной электронной микроскопии (2D STEM) позволяют определить площадь частицы \(A\) и присвоить ей диаметр, предполагая сферическую форму \(\left(\text{т.е.}~{}A=\pi R^{2}\right)\). Различные частицы с незначительными отклонениями от сферической формы могут иметь одинаковую площадь и, в конечном итоге, одинаковый диаметр. Однако их энергии резонанса SP различаются, и это мы наблюдаем экспериментально. Вторая важная особенность - существенное синее смещение энергии резонанса на 0.5 эВ при уменьшении диаметра частицы. Это смещение синее смещение хорошо согласуется с ранее полученными результатами [24, 26, 27]. Классическая теория локального отклика на основе независимой от размера диэлектрической функции материала не предсказывает никакого смещения частоты. Рисунок 3(b) снова показывает энергию резонанса SP \(E\) как функцию обратного диаметра частицы \(1/(2R)\). Экспериментальные измерения указывают на линейную зависимость между энергией и обратным диаметром частицы. Почти линейная тенденция также наблюдается в теоретических расчетах на основе гидродинамической модели, показанных прерывистыми и сплошными линиями на рис. 3(b), хотя с меньшим наклоном. Мы указываем на то, что видимая сдвигая длины волны, зависящая от \(1/(2R)\), - это только первое приближение в гидродинамической теории [1]. Пунктирная линия на рис. 3(b) соответствует расчетам гидродинамической сферы, встроенной в однородную среду, то есть нелокальный фактор Клаузиуса-Моссотти, описанный в разделе 3.1. Позволив фоновой диэлектрической проницаемости подогнаться под среднюю резонанс крупнейших частиц (\(2R>20~{}\text{нм}\)), чтобы обеспечить правильный классический резонанс SP, мы находим \(\varepsilon_{\textsc{b}}=1.53\). Сплошная линия показывает энергию резонанса, определенную на основе расчетов поперечного сечения поглощения гидродинамической сферы в вакууме, находящейся на подложке из Si\({}_{3}\)N\({}_{4}\) толщиной 10 нм, как описано в разделе 3.2. Здесь не выполняется подгонка фоновой диэлектрической проницаемости, и мы используем \(\varepsilon_{\textsc{s}}=4.4\) как проницаемость подложки, подходящую для Si\({}_{3}\)N\({}_{4}\)[44]. В обоих расчетах используются те же материальные параметры для сферы из Ag [45]. В сравнении с окружающей средой свободного пространства, наличие диэлектрической подложки должно вызвать больший сдвиг длины волны в гидродинамической модели [1], и это действительно так (сравнение не показано на рис. 3). Подогнанная эффективная фоновая диэлектрическая проницаемость в расчетах на основе связи Клаузиуса-Моссотти является больше, чем в свободном пространстве, и это приводит к тому, что две теоретические кривые на рис. 3(b) становятся практически параллельными. Особенно для самых маленьких частиц \(\left[1/(2R)>0.1~{}\text{нм}^{-1}\right]\) тенденция весьма схожа, что указывает на то, что (i) только дипольный режим сферы является важным и (ii) дипольный режим не существенно изменен наличием подложки. Однако для более крупных диаметров частицы \(\left[1/(2R)<0.1~{}\text{нм}^{-1}\right]\) подложка изменяет дипольный режим, что видно в небольшой выпуклой кривизне сплошной линии на рис. 3(b), в отличие от вогнутой кривизны пунктирной линии. Удивительно, что многочисленные мультиполи сферы, предполагаемые усиленными наличием подложки [46], не показывают существенный вклад в оптический отклик. Это связано со значительным межзонным поглощением в Ag в энергиях резонанса более высоких порядков мультиполей, что сильно затухляет вклад этих режимов. Из рис. 3(b) видно, что экспериментально наблюдаемое синее смещение превышает теоретическое синее смещение, предсказанное нелинейным фактором Клаузиуса-Моссотти. В работе [1] мы предположили, что присутствие подложки может вызывать экспериментально наблюдаемое большее синее смещение, но из рис. 3(b) мы видим более подробно, что расчеты на основе подложки не показывают большего смещения энергии, чем нелинейный фактор Клаузиуса-Моссотти. ## 5 Выводы Мы изучали экспериментально наблюдаемый сдвиг в сторону синего при граничной резонансной энергии у частиц серебра, когда их диаметр уменьшается с 26 нм до 3.5 нм. Чтобы интерпретировать измерения, мы рассмотрели две разные системы в рамках теории нелокальной гидродинамической модели: металлическую сферу в однородной среде и металлическую сферу, расположенную на диэлектрическом подложке конечной толщины. Удивительно, что оба этих систем дают схожие сдвиги в сторону синего с уменьшением размеров частиц, несмотря на наличие симметрии нарушающей подложки. Оба теоретических расчета качественно согласуются с измерениями, но теоретически рассчитанный сдвиг в сторону синего меньше, чем наблюдаемый в измерениях методом электронной энергетической потери. Таким образом, мы приходим к выводу, что включение подложки в теоретических расчетах не может качественно объяснить измерения. Это заставляет нас считать, что отклонения между теорией и экспериментом следует искать во внутренних свойствах серебра, таких как рассасывание электронов в сочетании с экранировкой от d-электронов [47, 48] и изменения в электронной зонной структуре, зависящие от размера [23], которые не учитываются в гидродинамическом описании. ## 6 Благодарности Мы благодарим профессоров У. Крайбига и А.-П. Яухо за стимулирующие дискуссии. Мы также признательны за помощь и сотрудничество из наших соавторов в работе [1]. Центр наноструктурного графена спонсируется Датским национальным исследовательским фондом, проект DNRF58. Мы выражаем благодарность фонду А. П. Мюллера и Частин Мак-Кинни Мюллера за вклад в создание Центра электронной наноскопии. Перевести маркдаун с английского на русский. Сохранить формулы: ```markdown Это _курсивный_ текст. Это **полужирный** текст. Это `код`. Список: - Пункт 1 - Пункт 2 - Пункт 3 Нумерованный список: 1. Пункт 1 2. Пункт 2 3. Пункт 3 Гиперссылка: [Текст ссылки](http://www.example.com) Формула встроенная в текст: . Большая формула: $$ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$ ```

# On the arithmetic of the BC-system Alain Connes Caterina Consani A. Connes: Collège de France 3, rue d’Ulm Paris, F-75005 France I.H.E.S. and Vanderbilt University [email protected] C. Consani: Mathematics Department Johns Hopkins University Baltimore, MD 21218 USA [email protected] ###### Abstract. For each prime \(p\) and each embedding \(\sigma\) of the multiplicative group of an algebraic closure of \({\mathbb{F}}_{p}\) as complex roots of unity, we construct a \(p\)-adic indecomposable representation \(\pi_{\sigma}\) of the integral BC-system as additive endomorphisms of the big Witt ring of \(\bar{\mathbb{F}}_{p}\). The obtained representations are the \(p\)-adic analogues of the complex, extremal KMS\({}_{\infty}\) states of the BC-system. The role of the Riemann zeta function, as partition function of the BC-system over \({\mathbb{C}}\) is replaced, in the \(p\)-adic case, by the \(p\)-adic \(L\)-functions and the polylogarithms whose values at roots of unity encode the KMS states. We use Iwasawa theory to extend the KMS theory to a covering of the completion \({\mathbb{C}}_{p}\) of an algebraic closure of \({\mathbb{Q}}_{p}\). We show that our previous work on the hyperring structure of the adèle class space, combines with \(p\)-adic analysis to refine the space of valuations on the cyclotomic extension of \({\mathbb{Q}}\) as a noncommutative space intimately related to the integral BC-system and whose arithmetic geometry comes close to fulfill the expectations of the “arithmetic site”. Finally, we explain how the integral BC-system appears naturally also in de Smit and Lenstra construction of the standard model of \(\bar{\mathbb{F}}_{p}\) which singles out the subsystem associated to the \(\hat{\mathbb{Z}}\)-extension of \({\mathbb{Q}}\). Key words and phrases: Witt rings, finite fields, BC-system 2000 Mathematics Subject Classification: 11M55, 46L55, 58B34 The authors are partially supported by the NSF grant DMS-FRG-0652164. The first author is grateful to Yves André for a helpful suggestion. The second author would like to thank the Institut des Hautes Études Scientifiques and the Collège de France for some financial support. ###### Contents Contents * 1 Introduction * 2 The functor \({\mathbb{W}}_{0}\) * 3 The integral BC-system * 4 \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) and the BC-system * 5 The Witt vectors functor and the truncation quotients * 6 The \(p\)-adic representations \(\pi_{\sigma}\) of the BC-system * 7 The KMS theory of the BC-system at a prime \(p\) * 7.1 The automorphisms \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) * 7.2 Cyclotomic identities for the polylogarithm * 7.3 The linear forms \(\varphi_{\beta,\rho}\) * 7.4 The KMS\({}_{\beta}\) condition * 7.5 Extension of the KMS\({}_{\beta}\) theory to the covering of \({\mathbb{C}}_{p}\) * 8 Extension of the \(p\)-adic valuation to \({{\mathbb{Q}}^{\rm cyc}}\) * 9 The base point problem and the “curve” for the global field \({\mathbb{Q}}\) * 9.1 Adelic interpretation of the loop groupoid \(\Pi_{1}^{\rm ab}(X)^{\prime}\) for function fields * 9.2 Fiber over a finite place of \({\mathbb{Q}}\) * 9.3 Fiber over the archimedean place of \({\mathbb{Q}}\) * 9.4 Ambient noncommutative space * 9.5 The BC-system over \({\mathbb{Z}}\) and \({\mathbb{F}}_{1^{\infty}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}\) * 10 The standard model of \(\bar{\mathbb{F}}_{p}\) and the BC-system ## 1. Introduction This paper describes several arithmetic properties of the BC-system, showing new and interesting connections with the theory of Witt vectors over the algebraic closure of finite fields and with p-adic analysis. The BC-system is a system of quantum statistical mechanics defined by a noncommutative Hecke algebra of double classes in \(P^{+}({\mathbb{Q}})\) with respect to the subgroup \(P^{+}({\mathbb{Z}})\), where \(P\subset GL_{2}\) is the “\(ax+b\)” algebraic group (_cf._[4, 9]). The complex Hecke algebra \({\mathcal{H}}_{\mathbb{C}}\) of the system has a highly non-trivial structure since its regular representation, in the Hilbert space of one sided classes, generates a factor of type III\({}_{1}\) and a canonical “time evolution” \(\sigma_{t}\in{\rm Aut}({\mathcal{H}}_{\mathbb{C}})\). The study of the KMS-equilibrium states at different temperatures has revealed the arithmetic nature of this dynamical system in view of the following facts \(\bullet\) The partition function of the system is the Riemann zeta function \(\bullet\) There is a phase transition with spontaneous symmetry breaking at the pole of zeta function \(\bullet\) The zero temperature vacuum states implement the global class field isomorphism for \({\mathbb{Q}}\). The study of the BC-system inaugurated the interplay between number-theory and noncommutative geometry. It is exactly the noncommutativity of the Hecke algebra of the system which generates its non-trivial dynamics. Moreover, on the noncommutative space of adèles classes \({\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}\), which is naturally associated to the type II dual of the BC-system, one obtains the spectral realization of zeros of \(L\)-functions and the trace formula interpretation of the Riemann-Weil explicit formulas (_cf._[7]). Further study (_cf._[15]) has shown that the integral Hecke algebra \({\mathcal{H}}_{\mathbb{Z}}={\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\rtimes{ \mathbb{N}}\) supplies an integral model to the BC-system. The endomorphisms \(\sigma_{n}(e(r))=e(nr)\), \(n\in{\mathbb{N}}\) act on the canonical generators \(e(r)\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), for \(r\in{\mathbb{Q}}/{\mathbb{Z}}\) and have natural linear quasi-inverses \[\tilde{\rho}_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}]\,,\ \ \tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{ \prime}=\gamma}e(\gamma^{\prime}),\] (1) which are used in the construction of the crossed product and in the presentation of the algebra. In this paper we establish, for each prime \(p\), a strong relation connecting the integral BC-system and the universal Witt ring \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) of an algebraic closure of a prime field. The Witt construction is in fact considered in the following three different forms \(-\) as a \(K\)-theory endofunctor \(A\mapsto{\mathbb{W}}_{0}(A)=K_{0}({\mbox{\text@underline{End}}}_{A})/K_{0}(A)\), in the category of commutative rings (with unit) \(-\) as the big Witt ring \({\mathbb{W}}(A)\) \(-\) as the functor \(A\mapsto{\mathbb{W}}_{p^{\infty}}(A)\), for \(A\) of characteristic \(p\). In the first two cases, the key structures are provided by the following operators \(-\) the Teichmüller multiplicative lift \(\tau:A\to{\mathbb{W}}_{0}(A)\) \(-\) the Frobenius endomorphisms \(F_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\), \(n\in{\mathbb{N}}\) \(-\) the Verschiebung additive functorial maps \(V_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\), \(n\in{\mathbb{N}}\) \(-\) the \(n\)-th ghost components \({\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A\), \(n\in{\mathbb{N}}\). These basic operators extend from the universal ring \({\mathbb{W}}_{0}(A)\) to its completion \({\mathbb{W}}(A)\) whose elements are expressed by Witt vectors, in terms of which all the algebraic operations can be defined in terms of polynomials with integral coefficients. This integrality property encodes a rich and deep arithmetical information. Moreover, the ring structure restricts to divisor stable subsets of \({\mathbb{N}}\) yielding, for the set of powers of a prime \(p\), the functor \({\mathbb{W}}_{p^{\infty}}\). In Proposition 4.4 and Theorem 4.5 we prove that the \(p\)-primary structure of the integral BC-system is completely encoded by the universal ring \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), with a precise dictionary expressing the key operators \(\sigma_{n}\) and \(\tilde{\rho}_{n}\) of the BC-system as respectively the Frobenius \(F_{n}\) and Verschiebung \(V_{n}\) on \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). The isomorphism connecting these algebraic structures depends upon the choice of a group isomorphism of the multiplicative group of \(\bar{\mathbb{F}}_{p}\) with the group of _complex_ roots of unity of order prime to \(p\): the ambiguity inherent to this choice is the same as that pertaining to the construction of Brauer lift of characters. The completion process associated to the inclusion \({\mathbb{W}}_{0}(A)\subset{\mathbb{W}}(A)\) with dense image, is then used in Theorem 6.4 to obtain, when \(A=\bar{\mathbb{F}}_{p}\) and for each injective group homomorphism \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{C}}^{\times}\), a \(p\)-adic _indecomposable_ representation \(\pi_{\sigma}\) of the integral BC-system as additive endomorphisms of the big Witt ring \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). The construction uses the identification proven in Theorem 4.5 and the implementation of the Artin–Hasse exponentials. These representations are the \(p\)-adic analogues of the complex, extremal KMS\({}_{\infty}\) states of the BC-system. In Section 7 this analogy is pursued much further. By implementing the theory of \(p\)-adic \(L\)-functions, we construct an analogue, in the \(p\)-adic case, of the partition function and of the KMS\({}_{\beta}\) states. In particular, we show that the division relations for the \(p\)-adic polylogarithms at roots of unity correspond to the KMS condition. In §7.5 we prove that the definition of the functionals satisfying such condition extends from the standard “extended s-disk” to the natural multiplicative group covering of \({\mathbb{C}}_{p}\). These results are the \(p\)-adic counterparts of the statements proven in [17] for function fields. However, we also recognize an important difference with respect to the complex case, namely the presence of an added symmetry at non-zero temperature, due to the invariance of the states under the natural involution of \({{\mathbb{Q}}^{\rm cyc}}\) which replaces each root of unity by its inverse. This added symmetry is a consequence of the vanishing of the \(p\)-adic \(L\)-functions associated to odd Dirichlet characters. For \(p\) a prime number, the set \(X_{p}\) of all injective group homomorphisms \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{Q}}/{\mathbb{Z}}\) is the parameter space for the \(p\)-adic representations of the integral BC-system. In Section 8, we relate this set with the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) of extensions of the \(p\)-adic valuation to the maximal abelian field extension \({{\mathbb{Q}}^{\rm cyc}}\) of \({\mathbb{Q}}\). We view \({{\mathbb{Q}}^{\rm cyc}}\) as an abstract field defined as the quotient of the group ring \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) by the cyclotomic ideal (_cf._ Definition 8.1). Let \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) be the subgroup of \({\mathbb{Q}}/{\mathbb{Z}}\) of fractions with denominator prime to \(p\) and let \({\mathbb{Q}}^{\rm cyc,p}\) be the subfield (_i.e._ the inertia subfield) of \({{\mathbb{Q}}^{\rm cyc}}\) generated by the group \(\mu^{(p)}\sim{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) of roots of unity of order prime to \(p\). We describe canonical isomorphisms of \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) with each of the following spaces \((1)\) The space of sequences of irreducible polynomials \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), fulfilling the basic conditions of the Conway polynomials (_cf._ Theorem 8.7). \((2)\) The space \(\Sigma_{p}\) of bijections of the monoid \({{\mathcal{M}}{(p)}}=\mu^{(p)}\cup\{0\}\) commuting with their conjugates, as in Definition 8.5 (_cf._ Proposition 8.8). \((3)\) The space \({\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) of field homomorphisms, where \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) is the decomposition subfield, _i.e._ the fixed field under the Frobenius automorphism (_cf._ Proposition 8.12). \((4)\) The quotient of the space \(X_{p}\) by the action of \({\rm Gal}(\bar{\mathbb{F}}_{p})\) (_cf._ Proposition 8.14). \((5)\) The algebraic spectrum of the quotient algebra \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]/J_{p}\), where \(J_{p}\) is the reduction modulo \(p\) of the cyclotomic ideal (_cf._ Definition 8.1 and Proposition 8.16). For a global field \({\mathbb{K}}\) of positive characteristic (_i.e._ a function field associated to a projective, non-singular curve over a finite field \({\mathbb{F}}_{q}\)) it is a well known fact that the space of valuations of the maximal abelian extension \({\mathbb{K}}^{\rm ab}\) of \({\mathbb{K}}\) has a geometric meaning. In fact, for each finite extension \(E\) of \(\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}}\subset{\mathbb{K}}^ {\rm ab}\), the space \({\rm Val}(E)\) of (discrete) valuations of \(E\) is an algebraic, one-dimensional scheme whose non-empty open sets are the complements of the finite subsets \(F\subset{\rm Val}(E)\). The structure sheaf is locally defined by the intersection \(\bigcap_{F}R\) of the valuation rings inside \(E\). Then the space \({\rm Val}({\mathbb{K}}^{\rm ab})\) is the projective limit of the schemes \({\rm Val}(E)\), \(E\subset{\mathbb{K}}^{\rm ab}\). For the global field \({\mathbb{K}}={\mathbb{Q}}\) of rational numbers, one can consider its maximal abelian extension \({{\mathbb{Q}}^{\rm cyc}}\) as an abstract field and try to follow a similar idea. In Section 9, we show however that the space \({\rm Val}({{\mathbb{Q}}^{\rm cyc}})\) provides only a rough analogue, in characteristic zero, of \({\rm Val}({\mathbb{K}}^{\rm ab})\). Our approach to this problem is guided and motivated by the following three results contained in our previous work \((a)\) The adelic interpretation of the loop groupoid \(\Pi_{1}^{\rm ab}(X)^{\prime}\) of the abelian cover of the algebraic curve \(X\) associated to a function field (_cf._[13] and § 9.1) \((b)\) The determination of the counting function \(N(q)\) (a distribution on \([1,\infty)\)) which replaces, for \({\mathbb{K}}={\mathbb{Q}}\), the classical Weil counting function for a function field (_cf._[11] and § 9.4) \((c)\) The interpretation of the counting function \(N(q)\) as an intersection number, using the action of the idèle class group on the adèle class space (_cf._[14]). By applying these results we find that the sought for geometric fiber over a non-archimedean, rational prime \(p\) is the total space of a principal bundle, with base \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and structure group given by a connected, compact solenoid \(S\) whose definition is given in Proposition 9.2. Then, in Proposition 9.3 we derive a natural construction for the fiber as the mapping torus \(Y_{p}\) of the action of the Frobenius on the space \(X_{p}\). In Section 9.3, we consider the fiber \(Y_{\infty}\) over the archimedean prime, with the implementation of the theory of multiplicative norms. The interpretation given in \((c)\) for the counting function as intersection number shows that the fibers \(Y_{p}\) should not be considered in isolation, but as being part of an ambient noncommutative space which is responsible for the transversality factors due to the archimedean contribution to the explicit formulas. This interpretation is explained in details in Section 9.4. In Section 9.5, we show that the integral BC-system gives, for each \(p\) (including the archimedean prime), a natural embedding of the fiber \(Y_{p}\) into a noncommutative space constructed using the set \({\mathcal{E}}({\mathbb{C}}_{p})\) of the \({\mathbb{C}}_{p}\)-rational points of the affine group scheme \({\mathcal{E}}\) which defines the abelian part of the system (_cf._[15]). Here \({\mathbb{C}}_{p}\) denotes the \(p\)-adic completion of an algebraic closure of \({\mathbb{Q}}_{p}\). This result shows that the space \[X({\mathbb{C}}_{p}):=\left({\mathcal{E}}({\mathbb{C}}_{p})\times(0,\infty) \right)/({\mathbb{N}}\times\{\pm 1\})\] (2) matches, for any rational prime \(p\) including \(p=\infty\), the definition of the adèle class space. In Proposition 9.5 we show, using the fact that \({\mathcal{E}}\) is a group scheme, that \(X({\mathbb{C}}_{p})\) is a free module of rank one over the hyperring \({\mathbb{H}}_{\mathbb{Q}}\) of the adèle classes. The problem of a correct interpretation of the connected factor \((0,\infty)\) in (2) remains open. It is a general principle that in our constructions the noncommutative spaces arise as \(X(A)\) for a commutative ring \(A\) (_cf._ (2)), while the classical subspaces of \(X(A)\) are defined as the support of the cyclotomic ideal (in the affine scheme \({\mathcal{E}}={\rm Spec}\,({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}])\)). We end the paper by showing in Section 10 the relevance of the recent work of B. de Smit and H. Lenstra (_cf._[18]) on the “standard model” for the algebraic closure of a finite field. When \({\mathbb{K}}\) is a function field, the intermediate extension \({\mathbb{K}}\subset L=\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K }}\subset{\mathbb{K}}^{\rm ab}\) plays an important geometric role, namely the extension of scalars to an algebraically closed field, for the algebraic curve associated to \({\mathbb{K}}\). When \({\mathbb{K}}={\mathbb{Q}}\), we show that the intermediate extension \({\mathbb{Q}}\subset{{\mathbb{Q}}^{\rm cycl}_{\Delta}}\subset{{\mathbb{Q}}^{\rm cyc}}\) used by de Smit and Lenstra, comes very close to fulfill the expected properties for a similar intermediate extension \({\mathbb{Q}}\subset L\subset{{\mathbb{Q}}^{\rm cyc}}\). Their construction provides a conceptual construction of the subfield of \(\bar{\mathbb{F}}_{p}\) union of all extensions whose degree is prime to \(p\). In the very last part of the paper we recall one of the first applications provided by E. Witt of his functor, which is a conceptual construction of the missing piece \(\bigcup_{n}{\mathbb{F}}_{p^{p^{n}}}\subset\bar{\mathbb{F}}_{p}\), using the simple equation \(X^{p}=X+1\) in Witt vectors. ## 2. The functor \({\mathbb{W}}_{0}\) In this section we recall the definition and the main properties of the universal ring \({\mathbb{W}}_{0}(A)\), where \(A\) is any commutative ring with unit. We refer to [1] to read more details. The second part of the section describes \({\mathbb{W}}_{0}(k)\), for an algebraically closed field \(k\). One lets \({\mbox{\text@underline{End}}}_{A}\) (or \(\text{End}~{}{\mathcal{P}}(A)\)) be the category of endomorphisms of projective \(A\)-modules of finite rank. The objects are pairs \((E,f)\) where \(E\) is a finite, projective \(A\)-module and \(f\in{\mbox{End}}_{A}(E)\). The morphisms in this category are required to commute with the endomorphisms \(f\). The following operations of direct sum and tensor product \[(E_{1},f_{1})\oplus(E_{2},f_{2})=(E_{1}\oplus E_{2},f_{1}\oplus f_{2})\,,\ \ ( E_{1},f_{1})\otimes(E_{2},f_{2})=(E_{1}\otimes E_{2},f_{1}\otimes f_{2})\] (3) turn the Grothendieck group \(K_{0}({\mbox{\text@underline{End}}}_{A})\) into a (commutative) ring. The pairs of the form \((E,f=0)\) generate the ideal \(K_{0}(A)\subset K_{0}({\mbox{\text@underline{End}}}_{A})\). We denote the quotient ring by \({\mathbb{W}}_{0}(A)\) \[{\mathbb{W}}_{0}(A)=K_{0}({\mbox{\text@underline{End}}}_{A})/K_{0}(A).\] (4) By construction, \({\mathbb{W}}_{0}\) is an endofunctor of the category \(\mathfrak{Ring}\) of commutative rings with unit. Several key operators and maps act on \({\mathbb{W}}_{0}\), the following are the most relevant ones for our applications \((1)\) The Teichmüller lift \(\tau:A\to{\mathbb{W}}_{0}(A)\) which is a multiplicative map. \((2)\) For \(n\in{\mathbb{N}}\), the Frobenius ring endomorphisms \(F_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\). \((3)\) For \(n\in{\mathbb{N}}\), the Verschiebung (shift) additive functorial maps \(V_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\). \((4)\) For \(n\in{\mathbb{N}}\), the \(n\)-th ghost component homomorphisms \({\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A\). We shortly recall their definitions. \((1)\) The Teichmüller lift \(\tau=[\cdot]:A\to{\mathbb{W}}_{0}(A)\) is defined as \(f\mapsto\tau(f)=[f]=(A,f)\). \((2)\) For \(n\in{\mathbb{N}}\), the operations in \({\mbox{\text@underline{End}}}_{A}\) of raising an endomorphism \(f\) to the \(n\)-th power induce the Frobenius ring endomorphims in \({\mathbb{W}}_{0}(A)\) \[F_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A),\qquad F_{n}(E,f)=(E,f^{n}).\] (5) \((3)\) For \(n\in{\mathbb{N}}\), the Verschiebung maps are defined by the following operations on matrices \[V_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A),\qquad V_{n}(E,f)=(E^{\oplus n },\begin{bmatrix}0&0&\cdots&\cdots&f\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}).\] (6) \((4)\) For \(n\in{\mathbb{N}}\), the ghost components are given by \[{\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A,\quad{\rm gh}_{n}(E,f)={\rm Trace}(f^{n}).\] (7) Let \(\Lambda(A):=1+tA[[t]]\) be the multiplicative abelian group of formal power series with constant term \(1\). The (inverse of the) characteristic polynomial defines a homomorphism of abelian groups \[L:{\mathbb{W}}_{0}(A)\to\Lambda(A),\quad L(E,f)=\det(1-tM(f))^{-1}\] (8) where \(M(f)=(a_{ij})\) is the matrix associated to \(f:E\to E\) (_i.e._\(f~{}\leftrightarrow~{}\sum_{i}x_{i}^{*}\otimes x_{i}\), \(x_{i}^{*}\in E^{*},x_{i}\in E\), \(a_{ij}=\langle x_{i}^{*},x_{j}\rangle\)). By a fundamental result of G. Almkvist ([1] Theorem 6.4 or [2] Main Theorem), one has **Theorem 2.1****.**: _The map \(L\) is injective and its image is the subgroup of \(\Lambda(A)\)_ \[{\rm Range}(L)=\{(1+a_{1}t+\ldots+a_{n}t^{n})/(1+b_{1}t+\ldots+b_{n}t^{n})\mid a _{j},b_{j}\in A\}.\] (9) Note in particular that for \(E\) a finite, projective \(A\)-module and \(f,g\in{\mbox{End}}_{A}(E)\) one has \[(E,fg)=(E,gf)\in{\mathbb{W}}_{0}(A).\] (10) One also has \[V_{nm}=V_{n}\circ V_{m}=V_{m}\circ V_{n}\,,\ \ F_{nm}=F_{n}\circ F_{m}=F_{m} \circ F_{n}.\] (11) The following proposition collects together several standard equations connecting these operators **Proposition 2.2****.**: _Let \(A\) be a commutative ring and \(x,y\in{\mathbb{W}}_{0}(A)\). The following hold_ \((1)\)_\(F_{n}\circ V_{n}(x)=nx\)._ \((2)\)_\(V_{n}(F_{n}(x)y)=xV_{n}(y)\)._ \((3)\) _If \((m,n)=1\), \(V_{m}\circ F_{n}=F_{n}\circ V_{m}\)._ \((4)\) _For \(n\in{\mathbb{N}}\), \(V_{n}(x)V_{n}(y)=nV_{n}(xy)\)._ \((5)\) _For \(n\in{\mathbb{N}}\), \(F_{n}(\tau(f))=\tau(f^{n})\)._ \((6)\) _For \(n,m\in{\mathbb{N}}\), \({\rm gh}_{n}(F_{m}(f))={\rm gh}_{nm}(f)\)._ \((7)\)_\({\rm gh}_{n}(V_{m}(f))=\begin{cases}m\,{\rm gh}_{n/m}(f)&\text{if $m|n$}\\ 0&\text{otherwise.}\end{cases}\)_ Proof.: All proofs are straightforward, we just check \((4)\) as an example. For \(x\in{\mbox{End}}_{A}(E)\), the action of \(X=V_{n}(E,x)\) on vectors \(\xi=(\xi_{1},\ldots,\xi_{n})\in E^{\oplus n}\) is given by \[(X\xi)_{1}=x\xi_{n}\,,\ \ (X\xi)_{j}=\xi_{j-1}\,,\quad~{}\forall j,~{}2\leq j \leq n.\] Similar formulas hold for \(Y=V_{n}(F,y)\), for \(y\in{\mbox{End}}_{A}(F)\). By definition, \(V_{n}(x)V_{n}(y)\) corresponds to \(X\otimes Y\in{\mbox{End}}_{A}(E^{\oplus n}\otimes F^{\oplus n})\). This endomorphism decomposes as the direct sum of \(n\) endomorphisms of \((E\otimes F)^{\oplus n}\), each of these is of the form \[\begin{bmatrix}0&0&\cdots&\cdots&x\otimes 1\\ 1&0&0&\cdots&0\\ 0&1\otimes y&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix},\quad\text{or}\quad\begin{bmatrix}0&0&\cdots&\cdots&x \otimes y\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}.\] By applying (10), one checks that each of the above endomorphisms is equivalent to \(V_{n}(x\otimes y)\). The equality \(V_{n}(x)V_{n}(y)=nV_{n}(xy)\) follows.∎ We shall apply the following proposition to the case \(A=k=\bar{\mathbb{F}}_{p}\) an algebraic closure of \({\mathbb{F}}_{p}\). **Proposition 2.3****.**: _Let \(k\) be an algebraically closed field. Then the map which associates to \((E,f)\in{\mbox{\text@underline{End}}}_{k}\) the divisor \(\delta(f)\) of non-zero eigenvalues of \(f\) (with multiplicity taken into account) extends to a ring isomorphism_ \[\delta:{\mathbb{W}}_{0}(k)\stackrel{{\sim}}{{\to}}{\mathbb{Z}}[k^{ \times}].\] (12) _Under the above isomorphism, the Frobenius \(F_{n}\) on \({\mathbb{W}}_{0}(k)\) is given on \({\mathbb{Z}}[k^{\times}]\) by the natural linearization of the group endomorphism \(k^{\times}\to k^{\times},~{}g\mapsto g^{n}\)._ Proof.: By applying Theorem 2.1, the characteristic polynomial extends to a complete invariant on \(K_{0}({\mbox{\text@underline{End}}}_{k})\) and to an isomorphism of \(K_{0}({\mbox{\text@underline{End}}}_{k})\) with the ring of quotients of monic polynomials in \(k[t]\). Moding out this ring by \(K_{0}(k)\) means that one removes the powers of the variable. Thus the divisor of non-zero eigenvalues of \(f\) extends to define a bijection of sets \({\mathbb{W}}_{0}(k)\simeq{\mathbb{Z}}[k^{\times}]\). It remains to check that this bijection preserves the ring operations. For addition, the set underlying the divisor \(\delta(f_{1}+f_{2})\) is the disjoint union of the two sets of roots of \(f_{j}\) and hence \(\delta(f_{1}+f_{2})=\delta(f_{1})+\delta(f_{2})\). For the product, it is enough and easy to check that the tensor product of two rank one elements \((k,a)\otimes(k,b)\) is given by \((k,ab)\) for non-zero elements of \(k\). The statement about \(F_{n}\) is checked in the same way using (5) on elements \((k,a)\). ∎ We recall the following formula for \(L(f)\) in terms of the divisor \(\delta(f)=\sum n(\alpha)[\alpha]\in{\mathbb{Z}}[k^{\times}]\) \[L(f)=\prod(1-\alpha\,t)^{-n(\alpha)}.\] (13) **Corollary 2.4****.**: _For any given isomorphism \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\stackrel{{\sim}}{{ \longrightarrow}}{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) of the multiplicative group of the algebraic closure \(\bar{\mathbb{F}}_{p}\) with the subgroup \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{\mathbb{Z}}\) of fractions with denominator prime to \(p\), one derives an isomorphism_ \[\tilde{\sigma}:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\stackrel{{ \sim}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}].\] (14) _Under the isomorphism \(\tilde{\sigma}\), the Frobenius \(F_{n}\) of \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) is given on \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) by the natural linearization of the group endomorphism \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), \(g\mapsto g^{n}\) (i.e. \(\gamma\mapsto n\gamma\) in additive notation)._ ## 3. The integral BC-system For each \(n\in{\mathbb{N}}\), one defines group ring endomorphisms \[\sigma_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{\mathbb{Q}} /{\mathbb{Z}}],\qquad\sigma_{n}(e(\gamma))=e(n\gamma)\] and the following additive maps \[\tilde{\rho}_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],\qquad\tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{ \prime}=\gamma}e(\gamma^{\prime}).\] (15) We recall from [15], Proposition 4.4, the following result **Proposition 3.1****.**: _The endomorphisms \(\sigma_{n}\) and the maps \(\tilde{\rho}_{m}\) fulfill the following relations_ \[\sigma_{nm}=\sigma_{n}\sigma_{m}\,,\ \ \tilde{\rho}_{mn}=\tilde{\rho}_{m} \tilde{\rho}_{n}\,,\quad~{}\forall m,n\in{\mathbb{N}}\] (16) \[\tilde{\rho}_{m}(\sigma_{m}(x)y)=x\tilde{\rho}_{m}(y)\,,\quad~{}\forall x,y\in {\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\] (17) \[\sigma_{c}(\tilde{\rho}_{b}(x))=(b,c)\,\tilde{\rho}_{b^{\prime}}(\sigma_{c^{ \prime}}(x))\,,\ \ b^{\prime}=b/(b,c)\,,\ \ c^{\prime}=c/(b,c)\,,\] (18) _where \((b,c)=\text{gcd}(b,c)\)._ Note that taking \(b=c=n\) in (18) gives \[\sigma_{n}(\tilde{\rho}_{n}(x))=n\,x\,,\quad~{}\forall x\in{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}].\] (19) On the contrary, if we take \(b=n\) and \(c=m\) to be relatively prime we get \[\sigma_{n}\circ\tilde{\rho}_{m}=\tilde{\rho}_{m}\circ\sigma_{n}.\] (20) We recall from [15] (Definition 4.7 and §4.2) the following facts. The integral \(BC\)-algebra is the algebra \({\mathcal{H}}_{\mathbb{Z}}={\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\rtimes_{ \tilde{\rho}}{\mathbb{N}}\) generated by the group ring \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), and by the elements \(\tilde{\mu}_{n}\) and \(\mu_{n}^{*}\), with \(n\in{\mathbb{N}}\), which satisfy the relations \[\begin{array}[]{l}\tilde{\mu}_{n}x\mu_{n}^{*}=\tilde{\rho}_{n}(x)\\[8.535827pt ] \mu_{n}^{*}x=\sigma_{n}(x)\mu_{n}^{*}\\[8.535827pt] x\tilde{\mu}_{n}=\tilde{\mu}_{n}\sigma_{n}(x),\end{array}\] (21) where \(\tilde{\rho}_{m}\), \(m\in{\mathbb{N}}\) is defined in (15), as well as the relations \[\begin{array}[]{l}\tilde{\mu}_{nm}=\tilde{\mu}_{n}\tilde{\mu}_{m}\,,\quad~{} \forall n,m\in{\mathbb{N}}\\[8.535827pt] \mu_{nm}^{*}=\mu_{n}^{*}\mu_{m}^{*}\,,\quad~{}\forall n,m\\[8.535827pt] \mu_{n}^{*}\tilde{\mu}_{n}=n\\[8.535827pt] \tilde{\mu}_{n}\mu_{m}^{*}=\mu_{m}^{*}\tilde{\mu}_{n}\ \ \ \ (n,m)=1.\end{array}\] (22) After tensoring by \({\mathbb{Q}}\), the Hecke algebra \({\mathcal{H}}_{\mathbb{Q}}={\mathcal{H}}_{\mathbb{Z}}\otimes_{\mathbb{Z}}{ \mathbb{Q}}\) has a simpler explicit presentation with generators \(\mu_{n}(=\frac{1}{n}\tilde{\mu}_{n})\), \(\mu_{n}^{*}\), \(n\in{\mathbb{N}}\) and \(e(r)\), for \(r\in{\mathbb{Q}}/{\mathbb{Z}}\), satisfying the relations \(\bullet\)\(\mu_{n}^{*}\mu_{n}=1\), \(\forall n\in{\mathbb{N}}\), \(\bullet\)\(\mu_{m}\mu_{n}=\mu_{mn}\), \(\mu^{*}_{m}\mu^{*}_{n}=\mu^{*}_{mn}\), \(\forall m,n\in{\mathbb{N}}\), \(\bullet\)\(\mu_{n}\mu_{m}^{*}=\mu_{m}^{*}\mu_{n}\), if \((n,m)=1\), \(\bullet\)\(e(0)=1\), \(e(r)^{*}=e(-r)\), and \(e(r)e(s)=e(r+s)\), \(\forall r,s\in{\mathbb{Q}}/{\mathbb{Z}}\), \(\bullet\) For all \(n\in{\mathbb{N}}\) and all \(r\in{\mathbb{Q}}/{\mathbb{Z}}\) \[\mu_{n}\,e(r)\,\mu_{n}^{*}=\frac{1}{n}\sum_{ns=r}e(s).\] (23) After tensoring by \({\mathbb{C}}\) and completion one gets a \(C^{*}\)-algebra with a natural time evolution \(\sigma_{t}\) ([4], [16] Chapter III). The extremal KMS states below critical temperature vanish on the monomials \(\mu_{n}x\mu_{m}^{*}\) for \(n\neq m\) and \(x\in{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) and their value on \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) is given by \[\varphi_{\beta,\rho}(e(a/b))=\frac{1}{\zeta(\beta)}\sum_{n=1}^{\infty}n^{- \beta}\rho(\zeta_{a/b}^{n}),\] (24) where \(\rho\in\hat{\mathbb{Z}}^{*}\) determines an embedding in \({\mathbb{C}}\) of the cyclotomic field \({{\mathbb{Q}}^{\rm cyc}}\) generated by the abstract roots of unity. ## 4. \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) and the BC-system In [29] Quillen makes use of the choice of an embedding \[\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{C}}^{\times}\] (25) in the study of the algebraic K-theory of the general linear group over a finite field. In this section we compare the description of the universal Witt ring \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), endowed with the structure given by the Frobenius endomorphisms \(F_{n}\) and the Verschiebung maps \(V_{n}\) with the integral BC-algebra \({\mathcal{H}}_{\mathbb{Z}}\). By a simple comparison process we notice that the relations (16), (17), (18) holding on \({\mathcal{H}}_{\mathbb{Z}}\) are the same as those fulfilled by the Frobenius endomorphisms \(F_{n}\) and the Verschiebung maps \(V_{n}\) on \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). More precisely, under the correspondences \(\sigma_{n}\to F_{n}\), \(\tilde{\rho}_{n}\to V_{n}\) the two relations of (11) correspond to (16), and the first three relations of Proposition 2.2 correspond respectively to (19), (17) and (20). These results evidently point out to the existence of a strong relation between the (\(\lambda\))-ring \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) and the group ring \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) endowed with the aforementioned operators. Next, we compare the two groups rings: \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) and \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) which arise in the description of \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) and in the construction of the BC-algebra respectively. One has a surjective group homomorphism: \({\mathbb{Q}}/{\mathbb{Z}}\to{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) induced by the canonical factorization of the groups \[{\mathbb{Q}}/{\mathbb{Z}}={({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\times{\mathbb{Q} }_{p}/{\mathbb{Z}}_{p}\] (26) where \({\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}\) is the group of fractions whose denominator is a power of \(p\). Thus one obtains a corresponding factorization of the rings \[{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]={\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z }})^{(p)}}]\otimes_{\mathbb{Z}}{\mathbb{Z}}[{\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}].\] (27) By using the trivial representation of \({\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}\) (_i.e._ the augmentation \(\epsilon\) of \({\mathbb{Z}}[{\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}]\)), one gets a retraction \(r=id\otimes\epsilon\) producing the splitting \[{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\stackrel{{ j_{p} }}{{\longrightarrow}}{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\stackrel{{ id\otimes\epsilon}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}} /{\mathbb{Z}})^{(p)}}].\] (28) Notice that \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) is preserved by the action of the map \(\gamma\mapsto n\gamma\), \(\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\)). This implies that the endomorphisms \(\sigma_{n}\) acting on the BC-algebra restrict naturally to determine endomorphisms \(\sigma_{n}:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Z}}[{( {\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\). Let us denote by \(I(p)\subset{\mathbb{N}}\) the set of integers which are prime to \(p\). The following lemma describes the projection of the operators \(\tilde{\rho}_{n}\) of the BC-algebra on the group ring \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) **Proposition 4.1****.**: _Let \(n=p^{k}m\), with \(m\in I(p)\). For \(\gamma\in{\mathbb{Q}}/{\mathbb{Z}}\), we write modulo \(1\)_ \[\gamma=\frac{a}{b}+\frac{c}{p^{s}}\,,\ b\in I(p)\,,\ a,b,c,s\in{\mathbb{N}}.\] (29) _Then, with \(\tilde{\rho}_{n}\) as in (15) we have_ \[r\circ\tilde{\rho}_{n}(e(\gamma))=p^{k}\sum_{w=0}^{m-1}e(\frac{f+wb}{bm})\] (30) _where \(y=\frac{f}{bm}\), \(f\in{\mathbb{Z}}/bm{\mathbb{Z}}\), is the unique solution in \({\mathbb{Q}}/{\mathbb{Z}}\), with denominator prime to \(p\) of the equation_ \[p^{k}y=\frac{a}{bm}\in{\mathbb{Q}}/{\mathbb{Z}}.\] (31) Proof.: The existence and uniqueness of the decomposition (29) derives from the factorization (26). For \(d\in I(p)\), the endomorphism of \({\mathbb{Q}}/{\mathbb{Z}}\): \(x\mapsto px\) restricts to an automorphism on the subgroup \(G_{d}=\{\frac{a}{d}\in{\mathbb{Q}}/{\mathbb{Z}}|\,a\in{\mathbb{Z}}\}\subset{ \mathbb{Q}}/{\mathbb{Z}}\). For \(d=bm\), this fact shows the existence and uniqueness of the solution \(y=\frac{f}{bm}\) of (31). One has \(p^{k}y=\frac{a}{bm}+j\) for some integer \(j\in{\mathbb{Z}}\), thus \[y=\frac{a}{bmp^{k}}+\frac{j}{p^{k}}=\frac{a}{bn}+\frac{j}{p^{k}},\ \ ny=\frac{ a}{b}+jm.\] By applying (26), one also has a decomposition of the form \[\frac{c}{np^{s}}=\frac{c}{mp^{s+k}}=\frac{d}{m}+\frac{e}{p^{s+k}}.\] (32) One has \(ny=\frac{a}{b}\) modulo \(1\), \(n\frac{c}{np^{s}}=\frac{c}{p^{s}}\), thus the solutions of the equation \(n\gamma^{\prime}=\gamma\) in \({\mathbb{Q}}/{\mathbb{Z}}\) which enter in (15) are of the form \[\gamma^{\prime}=y+\frac{c}{np^{s}}+\frac{u}{m}+\frac{v}{p^{k}}\,,\ \ u\in\{0, \ldots,m-1\}\,,\ v\in\{0,\ldots,p^{k}-1\}.\] By using (32) one derives \[\gamma^{\prime}=y+\frac{u}{m}+\frac{d}{m}+\frac{v}{p^{k}}+\frac{e}{p^{s+k}}\,, \ \ u\in\{0,\ldots,m-1\}\,,\ v\in\{0,\ldots,p^{k}-1\}.\] For the projection \(r(e(\gamma^{\prime}))\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) one thus gets that \[r(e(\gamma^{\prime}))=e(y+\frac{w}{m})=e(\frac{f+wb}{bm})\,,\ \ w\in\{0,\ldots ,m-1\}\\] which is repeated with multiplicity \(p^{k}\). The equation (30) follows. ∎ **Corollary 4.2****.**: _One has_ \[r\circ\tilde{\rho}_{n}(x)=r\circ\tilde{\rho}_{n}(r(x))\,,\quad~{}\forall x\in{ \mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\,,\ n\in{\mathbb{N}}.\] (33) _and_ \[r\circ\tilde{\rho}_{p^{k}}(x)=p^{k}\sigma_{p^{k}}^{-1}(r(x))\,,\quad~{}\forall x \in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],~{}k\in{\mathbb{N}}\,.\] (34) Proof.: The two statements follow from (30).∎ **Definition 4.3****.**: _For \(p\) a prime number, we denote by \(X_{p}\) the space of all injective group homomorphisms \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{Q}}/{\mathbb{Z}}\)._ The relation between \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) and the abelian part \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) of the integral BC-algebra \({\mathcal{H}}_{\mathbb{Z}}\) is described by the following lemma **Proposition 4.4****.**: _Let \(\sigma\in X_{p}\) and let \(\tilde{\sigma}\) be the associated ring isomorphism_ \[\tilde{\sigma}:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\stackrel{{ \sim}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] \subset{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}].\] _Then the Frobenius \(F_{n}\) and Verschiebung maps \(V_{n}\) on \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) are obtained by restriction of the ring endomorphisms \(\sigma_{n}\) and the maps \(\tilde{\rho}_{n}\) on \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) by the formulas_ \[\tilde{\sigma}\circ F_{n}=\sigma_{n}\circ\tilde{\sigma}\,,\ \ \tilde{\sigma} \circ V_{n}=r\circ\tilde{\rho}_{n}\circ\tilde{\sigma}.\] (35) Proof.: In section 2 we recalled (_cf._[19] for details) that the Frobenius \(F_{n}\) on \({\mathbb{W}}_{0}(A)\) is given by \(F_{n}(E,f)=(E,f^{n})\). At the level of the divisor of the eigenvalues of \(f\) (it is a divisor in the virtual case), _i.e._ at the level of the associated element in \({\mathbb{Z}}[k^{\times}]\), \(A=k=\bar{\mathbb{F}}_{p}\), the Frobenius \(F_{n}\) corresponds to the group homomorphism \(g\mapsto g^{n}\) (_cf._ Proposition 2.3). The Verschiebung maps \(V_{n}\) are described by the operation (6) on matrices. The maps \(V_{n}\) are additive and hence determined by the elements \(V_{n}([\alpha])\) where \(\alpha\in k^{\times}\). They correspond to the \(n\) eigenvalues of the following matrix \[V_{n}(\alpha)=\begin{bmatrix}0&0&\cdots&\cdots&\alpha\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}.\] Since the \(n\)-th power of the above matrix is the multiplication by \(\alpha\), all its eigenvalues fulfill the equation \(\beta^{n}=\alpha\). In fact the characteristic polynomial of the above matrix is \(P(X)=X^{n}-\alpha\). Let \(n=p^{k}m\), where \(m\) is prime to \(p\). Since \(\bar{\mathbb{F}}_{p}\) is a perfect field, the root \(\alpha^{p^{-k}}\in\bar{\mathbb{F}}_{p}\) of \(X^{p^{k}}-\alpha\) is unique and it admits \(m\) distinct roots of order \(m\): \(\beta^{m}=\alpha^{p^{-k}}\), which are the \(m\) roots of \(P(X)\). They take the form \(\xi\beta_{0}\), with \(\xi^{m}=1\). Thus the corresponding divisor is \[\delta=\sum_{\xi^{m}=1}p^{k}[\xi\beta_{0}].\] (36) We now compare the above description of the divisor associated to \(V_{n}(E,f)\) with \(r\circ\tilde{\rho}_{n}(e(\gamma))\), where \(\gamma=\sigma(\alpha)=\frac{a}{b}\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset {\mathbb{Q}}/{\mathbb{Z}}\). The elements \(\xi\beta_{0}\in\bar{\mathbb{F}}_{p}\) are the \(m\) distinct roots of the equation \(X^{n}=\alpha\). Similarly, with the notations of (30), the elements \[\frac{f+wb}{bm}\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{ \mathbb{Z}},\ \ w\in\{0,\ldots,m-1\}\] are the \(m\) solutions in \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) of the equation \(nz=\gamma\). One thus gets \[\tilde{\sigma}(\delta)=p^{k}\sum_{w=0}^{m-1}e(\frac{f+wb}{bm}).\] Thus (30) shows that \[\tilde{\sigma}(V_{n}([\alpha]))=\tilde{\sigma}(\delta)=r\circ\tilde{\rho}_{n}( e(\gamma))=r\circ\tilde{\rho}_{n}\circ\tilde{\sigma}([\alpha]).\] ∎ **Theorem 4.5****.**: _Let \(\sigma\in X_{p}\). The following formulas define a representation \(\pi_{\sigma}\) of the integral BC-system \({\mathcal{H}}_{\mathbb{Z}}\) as additive endomorphisms of \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\)_ \[\pi_{\sigma}(x)\xi=\tilde{\sigma}^{-1}(r(x))\,\xi\,,\ \ \pi_{\sigma}(\mu_{n}^{ *})=F_{n}\,,\ \ \pi_{\sigma}(\tilde{\mu}_{n})=V_{n}\] (37) _for all \(\xi\in{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) and \(n\in{\mathbb{N}}\)._ Proof.: By construction \(x\mapsto\tilde{\sigma}^{-1}(r(x))\) is a homomorphism of the group ring \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) to \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) and hence, by composition with the left regular representation, \(\pi_{\sigma}\) gives a representation of \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\). The \(F_{n}\) and \(V_{n}\) are additive. It remains to check the relations (21) and (22). The latter ones follow from (11) for the first two, and from \((1)\) and \((3)\) of Proposition 2.2 for the last two. To check the first relation of (21) one needs to show that \[V_{n}\pi_{\sigma}(x)F_{n}=\pi_{\sigma}(\tilde{\rho}_{n}(x)).\] (38) One has \(\pi_{\sigma}(x)=\pi_{\sigma}(r(x))\) for all \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\). Thus, by applying (33), one can replace \(x\) by \(r(x)\) without changing both sides of the equation. Thus we can assume that \(x=\tilde{\sigma}(z)\) for some \(z\in{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). Then \(\pi_{\sigma}(x)\) is just the multiplication by \(z\). One has by (35) \[r\circ\tilde{\rho}_{n}(x)=r\circ\tilde{\rho}_{n}(\tilde{\sigma}(z))=\tilde{ \sigma}\circ V_{n}(z).\] Thus \(\pi_{\sigma}(\tilde{\rho}_{n}(x))\) is the multiplication by \(V_{n}(z)\) and (38) follows from \[V_{n}(zF_{n}(\xi))=V_{n}(z)\xi\,,\quad~{}\forall\xi\in{\mathbb{W}}_{0}(\bar{ \mathbb{F}}_{p})\] which is statement \((2)\) of Proposition 2.2. Let us check the other two relations of (21). The second one means \[F_{n}\pi_{\sigma}(x)=\pi_{\sigma}(\sigma_{n}(x))F_{n}\] and since \(r\circ\sigma_{n}=\sigma_{n}\circ r\) we can assume as before that \(x=\tilde{\sigma}(z)\), for some \(z\in{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). Then \(\pi_{\sigma}(x)\) is the multiplication by \(z\) and, by (35), \(\pi_{\sigma}(\sigma_{n}(x))\) is the multiplication by \(F_{n}(z)\). The required equality then follows since \(F_{n}\) is multiplicative. The last relation of (21) means \[\pi_{\sigma}(x)V_{n}=V_{n}\pi_{\sigma}(\sigma_{n}(x))\] and assuming \(x=\tilde{\sigma}(z)\) it reduces to \[zV_{n}(\xi)=V_{n}(F_{n}(z)\xi)\,,\quad~{}\forall\xi\in{\mathbb{W}}_{0}(\bar{ \mathbb{F}}_{p})\] which in turn follows from statement \((2)\) of Proposition 2.2.∎ ## 5. The Witt vectors functor and the truncation quotients In this section we provide a short overview on the construction of the universal Witt scheme in the form that is most suitable to the applications contained in this paper, for more details we refer to [39, 28, 6, 22, 3, 33, 24]. In the second part of the section we connect the universal ring \({\mathbb{W}}_{0}(A)\) with \({\mathbb{W}}(A)\). The construction of the ring of big Witt vectors (or generalized Witt vectors) is described by a covariant endofunctor \({\mathbb{W}}:\mathfrak{Ring}\to\mathfrak{Ring}\) in the category of commutative rings (with unit). For \(A\in{\rm obj}(\mathfrak{Ring})\), and as a functor to the category of sets, one defines \[{\mathbb{W}}(A)=A^{\mathbb{N}}=\{(x_{1},x_{2},x_{3},\ldots)|x_{i}\in A\}.\] To a truncation set \(N\subseteq{\mathbb{N}}\) (_i.e._ a subset of \({\mathbb{N}}\) which contains every positive divisor of each of its elements), one associates the truncated functor \[{\mathbb{W}}_{N}:\mathfrak{Ring}\to\mathfrak{Sets},\qquad{\mathbb{W}}_{N}(A)=A ^{N}.\] As a functor to the category of sets, \({\mathbb{W}}_{N}\) is left represented by the polynomial ring \(R_{N}={\mathbb{Z}}[x_{n}|n\in N]\). Then it follows that the big Witt vectors functor \({\mathbb{W}}={\mathbb{W}}_{\mathbb{N}}\) is left represented by the symmetric algebra \({\rm Symm}={\mathbb{Z}}[x_{1},x_{2},x_{3},\ldots]\) \[{\mathbb{W}}(A)={\mbox{Hom}}_{\mathfrak{Ring}}({\rm Symm},A)\qquad\forall A\in {\rm obj}(\mathfrak{Ring}).\] (39) As an endofunctor in the category of commutative rings \({\mathbb{W}}_{N}:\mathfrak{Ring}\to\mathfrak{Ring}\) is _uniquely_ determined by requiring that for any commutative ring \(A\) and for any \(n\in N\), the following map, called the \(n\)-th ghost component is a ring homomorphism \[gh_{n}:{\mathbb{W}}_{N}(A)\to A,\quad gh_{n}(x)=\sum_{d|n}dx_{d}^{n/d}.\] (40) For \(t\) a variable, the functorial bijection of sets \[\varphi_{A}:{\mathbb{W}}(A)\to\Lambda(A)=1+tA[[t]],\qquad x=(x_{n})_{n\in{ \mathbb{N}}}\mapsto f_{x}(t)=\prod_{n\in{\mathbb{N}}}(1-x_{n}t^{n})^{-1}\] (41) transports the ring structure from \({\mathbb{W}}(A)\) to the multiplicative abelian group \(\Lambda(A)\) of power series over \(A\) with constant term \(1\), under the usual multiplication of power series (the power series \(1\) acts as the identity element). In other words one has \[\varphi_{A}(x+y)=\varphi_{A}(x)\varphi_{A}(y)\qquad\forall x,y\in{\mathbb{W}}( A).\] To make the description of the corresponding product \(\star\) on \(\Lambda(A)\) more explicit one introduces first the \(n\)-ghost components \(w_{n}:\Lambda(A)\to A\), \(n\in{\mathbb{N}}\), which are defined by the formula \[w(f)=w(1+a_{1}t+a_{2}t^{2}+a_{3}t^{3}+\cdots)=w_{1}t+w_{2}t^{2}+\cdots=t\frac{ d}{dt}(\log(f(t))).\] For example, the first three ghost components are given by the universal formulas \[w_{1}(f)=a_{1},\quad w_{2}(f)=-a_{1}^{2}+2a_{2},\quad w_{3}(f)=a_{1}^{3}-3a_{1 }a_{2}+3a_{3}.\] For products of the form \(\prod_{k=1}^{m}(1-\xi_{k}t)^{-1}=1+a_{1}t+a_{2}t^{2}+\cdots=f(t)\) this means that \[w_{1}t+w_{2}t^{2}+w_{3}t^{3}+\cdots =t\frac{d}{dt}(\log(f(t)))=t\frac{d}{dt}\sum_{k=1}^{m}\log((1-\xi _{k}t)^{-1})=\] \[=\sum_{i=1}^{\infty}(\xi_{1}^{i}+\xi_{2}^{i}+\cdots+\xi_{m}^{i})t ^{i}=\sum_{i=1}^{\infty}p_{i}(\xi)t^{i}.\] Thus the ghost components are given by the power sums in the \(\xi_{k}\)’s. Then, the product \(\star\) on \(\Lambda(A)\) is _uniquely_ determined by requiring that these ghost components are (functorial) ring homomorphisms. In fact, distributivity and functoriality together force the multiplication of power series in \(\Lambda(A)\) be expressed by the following rule \[f(t)=\prod_{i}(1-\xi_{i}t)^{-1},\quad g(t)=\prod_{i}(1-\eta_{i}t)^{-1},\quad \Rightarrow\quad(f\star g)(t)=\prod_{i,j}(1-\xi_{i}\eta_{j}t)^{-1}\] (42) where \[t\frac{d}{dt}(\log(\prod_{i,j}(1-\xi_{i}\eta_{j}t)^{-1}))=\sum_{n=1}^{\infty}p _{n}(\xi)p_{n}(\eta)t^{n}.\] It follows that multiplication according to (42) translates into component-wise multiplication for the ghost components on \(\Lambda(A)\). It is expressed by explicit polynomials with integral coefficients of the form \[(1+\sum a_{n}t^{n})\star(1+\sum b_{n}t^{n})=1+a_{1}b_{1}t+\left(a_{1}^{2}b_{1} ^{2}-a_{2}b_{1}^{2}-a_{1}^{2}b_{2}+2a_{2}b_{2}\right)t^{2}+\\ +(a_{1}^{3}b_{1}^{3}-2a_{1}a_{2}b_{1}^{3}+a_{3}b_{1}^{3}-2a_{1}^{3}b_{1}b_{2}+ 5a_{1}a_{2}b_{1}b_{2}-3a_{3}b_{1}b_{2}+a_{1}^{3}b_{3}-3a_{1}a_{2}b_{3}+3a_{3}b _{3})t^{3}+\cdots\] The ghost components \(gh_{n}(x)\) of a Witt vector \(x=(x_{1},x_{2},x_{3},\ldots)\in{\mathbb{W}}(A)\) become the ghost components of \(\varphi_{A}(x)\), _i.e._ \[gh_{n}:{\mathbb{W}}(A)\to A,\quad gh_{n}(x)=w_{n}(\varphi_{A}(x)).\] (43) It follows that the bijection \(\varphi_{A}:{\mathbb{W}}(A)\to\Lambda(A)\) becomes a ring isomorphism. Note moreover that the homomorphism of abelian groups \(L:{\mathbb{W}}_{0}(A)\to\Lambda(A)\) of (8), preserves the product, _i.e._ \[L((E,f)\otimes(F,g))=L((E,f))\star L((F,g))\] (44) so that it defines an injective ring homomorphism. Two Witt vectors \(x,y\in{\mathbb{W}}(A)\) are added and multiplied by means of universal polynomials with integer coefficients \[x+_{{\mathbb{W}}}y=(\mu_{S,1}(x,y),\mu_{S,2}(x,y),\ldots),\quad x\times_{{ \mathbb{W}}}y=(\mu_{P,1}(x,y),\mu_{P,2}(x,y),\ldots).\] The polynomials \(\mu_{S,i},\mu_{P,j}\) are recursively computed using the ghost components by the formulas \[gh_{n}(\mu_{S,1}(x,y),\mu_{S,2}(x,y),\ldots)=gh_{n}(x)+gh_{n}(y),\] \[gh_{n}(\mu_{P,1}(x,y),\mu_{P,2}(x,y),\ldots)=gh_{n}(x)gh_{n}(y).\] Notice that the polynomials \(gh_{n}(x)\) depend only on the \(x_{d}\) for \(d\) a divisor of \(n\), hence the \(n\)-th addition and multiplication polynomials \(\mu_{S,n}\), \(\mu_{P,n}\) are polynomials that only involve the \(x_{d}\) and \(y_{d}\) with \(d\) a divisor of \(n\). Thus, for a truncation set \(N\subseteq{\mathbb{N}}\), the polynomial ring \(R_{N}={\mathbb{Z}}[x_{n}|n\in N]\) is a sub Hopf algebra and a sub co-ring object of \({\rm Symm}\), this means that it defines a quotient functor, which coincides with \({\mathbb{W}}_{N}\). This result applies in particular to the truncation set \(N=\{p^{n}\mid n\geq 0\}\), where \(p\) is a prime number. Thus the p-adic Witt vectors \({\mathbb{W}}_{p^{\infty}}(A)\) can be interpreted as a functorial quotient of the big Witt vectors (similarly one obtains \({\mathbb{W}}_{p^{n}}(A)\) as the p-adic Witt vectors of length \(n+1\)). The Teichmüller representative is a multiplicative map which defines a section to the ghost map \(gh_{1}\). If \(N\subset{\mathbb{N}}\) is a truncation set, the Teichmüller representative is defined as \[[\cdot]_{N}:A\to{\mathbb{W}}_{N}(A),\quad a\mapsto[a]_{N}=([a]_{N})_{n\in N}, \quad[a]_{N,n}=\begin{cases}a&\text{if $n=1$},\\ 0&\text{if $n>1$}.\end{cases}\] One has \(gh_{n}([a]_{N})=a^{n}\) for all \(n\in N\). On the functorial ring \({\mathbb{W}}(A)\) one can introduce several functorial operations which derive from (the large number of) ring endomorphisms of \({\rm Symm}\) and by applying the representability property (39). For instance, the Verschiebung (shift) additive functorial endomorphisms on \({\mathbb{W}}\) and its quotients, arise from the ring endomorphism \[{\bf V}_{n}:{\rm Symm}\to{\rm Symm}\,,\ \ x_{i}\mapsto\begin{cases}x_{i/n}& \text{if $i$ is divisible by $n$}\\ 0&\text{otherwise}\end{cases}\] which corresponds to the map \(f(t)\mapsto f(t^{n})\) in \(\Lambda(A)\). For \(N\subset{\mathbb{N}}\) a truncation set, the shift is the additive map given by \[V_{n}:{\mathbb{W}}_{N/n}(A)\to{\mathbb{W}}_{N}(A),\quad V_{n}((a_{d}|d\in N/n) )=(a_{m}^{\prime}|m\in N);~{}a_{m}^{\prime}=\begin{cases}a_{d}&\text{if $m=nd$ }\\ 0&\text{otherwise}\end{cases}\] where \(N/n=\{d\in{\mathbb{N}}|nd\in N\}\). This means that the composite with the ghost components is given by \[gh_{m}V_{n}=\begin{cases}ngh_{m/n}&\text{if $n$ divides $m$}\\ 0&\text{otherwise.}\end{cases}\] (45) The n-th Frobenius is the (unique) natural ring homomorphism \[F_{n}:{\mathbb{W}}_{N}(A)\to{\mathbb{W}}_{N/n}(A)\] which is defined on the ghost components by the formula \(gh_{r}F_{n}=gh_{rn}\). Thus by definition the n-th Frobenius map makes the following diagram commute \[\begin{CD}{\mathbb{W}}_{N}(A)@>{gh}>{}>A^{N}\\ @V{F_{n}}V{}V@V{}V{F_{n}^{gh}}V\\ {\mathbb{W}}_{N/n}(A)@>{gh}>{}>A^{N/n}\end{CD}\] where \(F_{n}^{gh}\) takes a sequence \((a_{m}|m\in N)\) to the sequence whose d-th component is \(a_{dn}\). At the level of the components \(x_{j}\) of a Witt vector \(x\in{\mathbb{W}}_{N}(A)\), the Frobenius \(F_{n}\) is given by polynomials with integral coefficients. For instance, the following are the first \(5\) components of \(F_{3}(x)\) \[F_{3}(x)_{1} = x_{1}^{3}+3x_{3}\] \[F_{3}(x)_{2} = x_{2}^{3}-3x_{1}^{3}x_{3}-3x_{3}^{2}+3x_{6}\] \[F_{3}(x)_{3} = -3x_{1}^{6}x_{3}-9x_{1}^{3}x_{3}^{2}-8x_{3}^{3}+3x_{9}\] \[F_{3}(x)_{4} = -3x_{1}^{9}x_{3}+3x_{1}^{3}x_{2}^{3}x_{3}-18x_{1}^{6}x_{3}^{2}+3x _{2}^{3}x_{3}^{2}-36x_{1}^{3}x_{3}^{3}\] \[-24x_{3}^{4}+x_{4}^{3}-3x_{2}^{3}x_{6}+9x_{1}^{3}x_{3}x_{6}+9x_{3 }^{2}x_{6}-3x_{6}^{2}+3x_{12}\] \[F_{3}(x)_{5} = -3x_{1}^{12}x_{3}-18x_{1}^{9}x_{3}^{2}-54x_{1}^{6}x_{3}^{3}-81x_{ 1}^{3}x_{3}^{4}-48x_{3}^{5}+x_{5}^{3}+3x_{15}.\] Note that when \(p\) is a rational prime one has (_cf._[30] Proposition 5.12) \[F_{p}(x)_{m}\equiv x_{m}^{p}~{}({\rm mod}~{}pA).\] (46) One also has (_cf._[30] Proposition 5.9) \[V_{nm}=V_{n}\circ V_{m}=V_{m}\circ V_{n}\,,\ \ F_{nm}=F_{n}\circ F_{m}=F_{m} \circ F_{n}\] (47) where for the maps \(F_{n}\) one assumes \(nN\subset N\) and \(mN\subset N\). Proposition 2.2 extends without change, (_cf._[30] Proposition 5.10). **Proposition 5.1****.**: _Let \(N\subset{\mathbb{N}}\) be a truncation set, and \(n\in N\) with \(nN\subset N\). Let \(A\) be a commutative ring and \(x,y\in{\mathbb{W}}_{N}(A)\). Then_ \((1)\)_\(F_{n}\circ V_{n}(x)=nx\)._ \((2)\)_\(V_{n}(F_{n}(x)y)=xV_{n}(y)\)._ \((3)\) _If \(m\) is prime to \(n\), one has \(V_{m}\circ F_{n}=F_{n}\circ V_{m}\)._ \((4)\) _One has \(V_{n}(x)V_{n}(y)=nV_{n}(xy)\)._ Proof.: We refer to [30] Proposition 5.10. The statement \((4)\) differs slightly from this reference, it can be checked directly using Proposition 2.2. It implies that when \(n\) is invertible in \({\mathbb{W}}_{N}(A)\) then \(\frac{1}{n}V_{n}\) defines a ring endomorphism.∎ It is important to see how the description of the universal ring \({\mathbb{W}}_{0}(A)\) fits with the definition of \({\mathbb{W}}(A)\). There is a canonical ring monomorphism \({\mathbb{W}}_{0}(A)\hookrightarrow{\mathbb{W}}(A)\) which is given as the composite of the injective ring homomorphism \(L:{\mathbb{W}}_{0}(A)\to\Lambda(A)\) as in (8) and of the ring isomorphism \(\varphi_{A}^{-1}:\Lambda(A)\stackrel{{\sim}}{{\to}}{\mathbb{W}}(A)\) (_cf._ (41)) \[{\mathbb{W}}_{0}(A)\to\Lambda(A)\simeq{\mathbb{W}}(A),\qquad(E,f)\mapsto\det(1 -tM(f))^{-1}.\] (48) In the case \(A=\bar{\mathbb{F}}_{p}\) the characteristic polynomial \(\det(1-tM(f))=\det(1-tf)\) factorizes as a product of terms \((1-t\alpha_{j})\) of degree one, where the \(\alpha_{j}\in\bar{\mathbb{F}}_{p}\) are the eigenvalues of \(f\) (_cf._ (13)). **Lemma 5.2****.**: _Let \([\cdot]:\bar{\mathbb{F}}_{p}\to{\mathbb{W}}(\bar{\mathbb{F}}_{p}),~{}x\mapsto \tau(x):=[x]\) be the Teichmüller lift and let \(\delta:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\to{\mathbb{Z}}[\bar{\mathbb{F}}_ {p}^{\times}]\) be the isomorphism of (12). Then the canonical map (48) is given explicitly as_ \[j:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\to{\mathbb{W}}(\bar{\mathbb{F}}_{p}), \quad j\circ\delta^{-1}:{\mathbb{Z}}[\bar{\mathbb{F}}_{p}^{\times}]\ni\sum n_{ j}\alpha_{j}\mapsto\sum n_{j}\tau(\alpha_{j})\in{\mathbb{W}}(\bar{\mathbb{F}}_ {p}).\] (49) This Lemma together with Theorem 2.1 shows that the subring \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\subset{\mathbb{W}}(\bar{\mathbb{F}}_{p})\) is just the group ring \({\mathbb{Z}}[\bar{\mathbb{F}}_{p}^{\times}]\) and is freely generated over \({\mathbb{Z}}\) by the Teichmüller lifts. ## 6. The \(p\)-adic representations \(\pi_{\sigma}\) of the BC-system In this section we shall implement the results of [6, 33, 3] to describe the ring \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\), then using the embedding with dense image \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\hookrightarrow{\mathbb{W}}(\bar{\mathbb {F}}_{p})\), we will extend the representation \(\pi_{\sigma}\) of \({\mathcal{H}}_{\mathbb{Z}}\) on \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) (Theorem 4.5) to a representation of the integral BC-system on \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). Such representation is the \(p\)-adic analogue of the irreducible complex representation (86). We begin by recalling the definition of the isomorphism \[{\mathbb{W}}(\bar{\mathbb{F}}_{p})\simeq{\mathbb{W}}_{p^{\infty}}(\bar{\mathbb {F}}_{p})^{I(p)}\] (50) where \(I(p)\subset{\mathbb{N}}\) is the set of positive integers which are prime to \(p\) and \(p^{\infty}\) is the set of integer powers of \(p\). At the conceptual level, this isomorphism is a special case of the general functorial isomorphism holding for any commutative ring \(A\) with unit ([3] Theorem 1) \[{\mathbb{W}}(A)={\mathbb{W}}_{I(p)}({\mathbb{W}}_{p^{\infty}}(A)).\] (51) When \(A\) is an \({\mathbb{F}}_{p}\)-algebra, every element of \(I(p)\) is invertible in \(B={\mathbb{W}}_{p^{\infty}}(A)\), thus one derives a canonical isomorphism \({\mathbb{W}}_{I(p)}(B)\simeq B^{I(p)}\) which is defined in terms of the ghost components. Let \({\mathbb{Z}}_{(p)}\) be the ring \({\mathbb{Z}}\) localized at the prime ideal \(p{\mathbb{Z}}\) so that every element of \(I(p)\) is invertible in \({\mathbb{Z}}_{(p)}\). A central role, in the ring \(\Lambda({\mathbb{Z}}_{(p)})\), is played by the Artin-Hasse exponential, this is the power series \[E_{p}(t)={\rm hexp}(t)={\rm exp}(t+\frac{t^{p}}{p}+\frac{t^{p^{2}}}{p^{2}}+ \cdots)\in\Lambda({\mathbb{Z}}_{(p)}).\] (52) The following properties are well known (_cf._[3, 33]) **Proposition 6.1****.**: \((1)\)_\(E_{p}(t)\) is an idempotent of \(\Lambda({\mathbb{Z}}_{(p)})\)._ \((2)\) _For \(n\in I(p)\), the series \(E_{p}(n)(t):=\frac{1}{n}V_{n}(E_{p})(t)\in\Lambda({\mathbb{Z}}_{(p)})\) determine an idempotent. As \(n\) varies in \(I(p)\), the \(E_{p}(n)\) form a partition of unity by idempotents._ \((3)\) _For \(n\notin p^{\mathbb{N}}\), \(F_{n}(E_{p})(t)=1(=0_{\Lambda})\) and \(F_{p^{k}}(E_{p})(t)=E_{p}(t)\), \(\forall k\in{\mathbb{N}}\)._ To check \((1)\) directly, one shows that there exists a unique sequence \((x_{n})_{n\in{\mathbb{N}}}\in{\mathbb{W}}({\mathbb{Z}}_{(p)})\) such that \(\bullet\)\(x_{1}=1\) \(\bullet\)\(x_{p^{k}}=0\) for all \(k>0\) \(\bullet\)\(F_{m}(x)_{p^{k}}=0\) for all \(m\in I(p)\) and \(k\geq 0\). This follows by noticing that the coefficient of \(x_{mp^{k}}\) in \(F_{m}(x)_{p^{k}}\) is \(m\in I(p)\) which is invertible in \({\mathbb{Z}}_{(p)}\), so that one determines the \(x_{n}\) inductively. One then checks that the ghost components of \((x_{n})_{n\in{\mathbb{N}}}\in{\mathbb{W}}({\mathbb{Z}}_{(p)})\) are the same as those of \(E_{p}(t)\), _i.e._\(gh_{n}(x)\) is equal to \(1\) if \(n\in p^{\mathbb{N}}\) and is zero otherwise. Note that any \(n\in I(p)\) is invertible in \(\Lambda({\mathbb{Z}}_{(p)})\). Division by \(n\) corresponds to the extraction of the \(n\)-th root of the power series \(f(t)=1+g(t)\). Formally, this is given by the binomial formula \[f^{\frac{1}{n}}=(1+g)^{\frac{1}{n}}=1+\frac{1}{n}g+\ldots+\frac{\frac{1}{n}( \frac{1}{n}-1)\cdots(\frac{1}{n}-k+1)}{k!}g^{k}+\ldots\] (53) The \(p\)-adic valuation of the rational coefficient of \(g^{k}\) is positive because \(\frac{1}{n}\in{\mathbb{Z}}_{p}\), thus this coefficient can be approximated arbitrarily by a binomial coefficient. It follows from Proposition 2.2, \((4)\) that \(\frac{1}{n}V_{n}\) is an endomorphism of \(\Lambda(\bar{\mathbb{F}}_{p})\) and also a right inverse of \(F_{n}\). One easily derives from [6, 3, 33] the following result **Proposition 6.2****.**: _Let \(A\) be an \({\mathbb{F}}_{p}\)-algebra._ \((a)\) _The map_ \[\psi_{A}:{\mathbb{W}}_{p^{\infty}}(A)\to\Lambda(A)_{E_{p}},\quad x=(x_{p^{n}}) _{n\in{\mathbb{N}}},\quad\psi_{A}(x)(t):=h_{x}(t)=\prod_{\mathbb{N}}E_{p}(x_{p ^{n}}t^{p^{n}})\] (54) _is an isomorphism onto the reduced ring \(\Lambda(A)_{E_{p}}=\{x\in\Lambda(A)\mid x\star E_{p}=x\}\)._ \((b)\) _For \(n\in I(p)\), the composite \(\psi_{A}^{-1}\circ F_{n}\) is an isomorphism of the reduced algebra \(\Lambda(A)_{E_{p}(n)}\) with \({\mathbb{W}}_{p^{\infty}}(A)\)._ \((c)\) _The composite_ \[\theta_{A}(x)=(\theta_{A}(x))_{n}=\psi_{A}^{-1}\circ F_{n}(x\star E_{p}(n)),\ \ n\in I(p),~{}x\in\Lambda(A)\] (55) _is a canonical isomorphism \(\theta_{A}:\Lambda(A)\to{\mathbb{W}}_{p^{\infty}}(A)^{I(p)}={\mathbb{W}}(A)\)._ \((d)\) _The composite isomorphism \(\Theta_{A}:=\theta_{A}\circ\varphi_{A}:{\mathbb{W}}(A)\to{\mathbb{W}}_{p^{ \infty}}(A)^{I(p)}\) is given explicitly on the components by_ \[(\Theta_{A}(x)_{n})_{p^{k}}=F_{n}(x)_{p^{k}}\,,\quad~{}\forall x\in{\mathbb{W} }(A)\,,\quad~{}\forall n\in I(p).\] (56) Proof.: The first three statements follow from [6] §3.b, [3], Thm. 1 and Prop. 1, [33] Thm. 9.15. We prove \((d)\). Since the Frobenius \(F_{n}\) is an endomorphism and \(F_{n}(x\star E_{p}(n))=F_{n}(x)\star E_{p}\), one can rewrite (55) as \[(\theta_{A}(x))_{n}=\psi_{A}^{-1}(E_{p}\star F_{n}(x))\,,\quad~{}\forall n\in I (p).\] (57) Thus, to show (56) it is enough to prove it for \(n=1\). One needs to check that for all \(x\in{\mathbb{W}}(A)\), one has \[E_{p}\star\varphi_{A}(x)=\prod_{\mathbb{N}}E_{p}(x_{p^{n}}t^{p^{n}}).\] Indeed, this follows from distributivity and the identity \[E_{p}\star(1-xt^{n})^{-1}=\left\{\begin{array}[]{ll}1&\hbox{if}\ n\notin p^{ \mathbb{N}}\\ E_{p}(xt^{p^{k}})&\hbox{if}\ n=p^{k}.\end{array}\right.\] The above identity can be checked directly knowing that \((1-xt^{n})^{-1}=V_{n}(\tau(x))\) and by applying the equality \[E_{p}\star(1-xt^{n})^{-1}=E_{p}\star V_{n}(\tau(x))=V_{n}(F_{n}(E_{p})\star \tau(x))\] together with Proposition 6.1\((3)\) and the equality \[\tau(y)\star f(t)=(1-yt)^{-1}\star f(t)=f(yt)\] which holds for any element \(f(t)\in\Lambda(A)\). In particular, for the Teichmüller lift \(\tau(y)=[y]\) of an element \(y\in A\) one gets \[\theta_{A}(\tau(y))_{n}=\tau(y^{n})\,,\quad~{}\forall n\in I(p)\] (58) where, on the right hand side, \(\tau\) denotes the original Teichmüller lift \(\tau:A\to{\mathbb{W}}_{p^{\infty}}(A)\). Indeed one has \(F_{n}(\tau(y))=\tau(y^{n})\).∎ **Corollary 6.3****.**: _Let \(A\) be an \({\mathbb{F}}_{p}\)-algebra. Then, the common fixed points of the endomorphisms \(F_{n}:{\mathbb{W}}(A)\to{\mathbb{W}}(A)\) for \(n\in I(p)\), are the elements of the form_ \[L(\lambda)=\sum_{m\in I(p)}\frac{1}{m}V_{m}(E_{p}\star\lambda)\,,\ \ \lambda \in{\mathbb{W}}_{p^{\infty}}(A).\] (59) _One also has_ \[\varphi_{A}(L(\lambda))=\prod_{n\in I(p)}h_{\lambda}(t^{n})^{\frac{1}{n}}.\] Proof.: Let \(x\in{\mathbb{W}}(A)\) with \(F_{n}(x)=x\) for all \(n\in I(p)\). Then, it follows from (56) and (55) that all the components \((\theta_{A}(x))_{n}\) are equal, so that for some \(\lambda\in{\mathbb{W}}_{p^{\infty}}(A)\) one has \[E_{p}(n)\star x=\frac{1}{n}V_{n}(E_{p}\star\lambda)\] and \(x\) is of the required form. Conversely, by Proposition 6.1\((3)\), one has \(F_{a}(E_{p})=0_{\Lambda}\) for all \(a\in I(p),\,a\neq 1\). Thus when one applies \(F_{k}\) to \(\frac{1}{n}V_{n}(E_{p}\star\lambda)\), one gets \(1(=0_{\Lambda})\) unless \(k|n\) using Proposition 5.1\((2)\), \((3)\). When \(k|n\) one obtains \(\frac{1}{m}V_{m}(E_{p}\star\lambda)\), with \(m=n/k\). Thus the elements of the form (59) are fixed under all \(F_{k}\). ∎ We now apply these results to the case \(A=\bar{\mathbb{F}}_{p}\). We identify \({\mathbb{W}}_{p^{\infty}}(\bar{\mathbb{F}}_{p})\) with a subring of \({\mathbb{C}}_{p}\) (the \(p\)-adic completion of an algebraic closure of \({\mathbb{Q}}_{p}\)). Let \(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}\subset{\mathbb{C}}_{p}\) be the completion of the maximal unramified extension of \({\mathbb{Q}}_{p}\). Then one knows that \({\mathbb{W}}_{p^{\infty}}(\bar{\mathbb{F}}_{p})={\mathcal{O}}_{\widehat{{ \mathbb{Q}}_{p}^{\rm ur}}}\) is the ring of integers of \(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}\). With \(\Theta\) the isomorphism of (56), we have \[\Theta:{\mathbb{W}}(\bar{\mathbb{F}}_{p})\stackrel{{\sim}}{{\to}}( {\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}})^{I(p)}\,,\ \ (\Theta(x)_{ n})_{p^{k}}=F_{n}(x)_{p^{k}},\quad\forall n\in I(p),~{}\forall x\in{\mathbb{W} }(\bar{\mathbb{F}}_{p}).\] (60) Thus \(\Theta\) makes \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\) a module over \({\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\). To the Frobenius automorphism of \(\bar{\mathbb{F}}_{p}\) corresponds, by functoriality, a canonical automorphism \({\rm Fr}\) of \({\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\) which extends to a continuous automorphism \[{\rm Fr}\in{\rm Aut}(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}).\] (61) We can now describe the \(p\)-adic analogues of the complex irreducible representations of the BC-system (_cf._ (86)). We recall that \(X_{p}\) denotes the space of all injective group homomorphisms \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{C}}^{\times}\). The choice of \(\sigma\in X_{p}\) determines an embedding \(\rho:{\mathbb{Q}}^{\rm cyc,p}\to{\mathbb{C}}_{p}\) of the cyclotomic field generated by the abstract roots of unity of order prime to \(p\) inside \({\mathbb{C}}_{p}\). In the following we shall use the simplified notation \({\mathcal{O}}={\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\). For \(m\in I(p)\), we let \(\epsilon_{m}\) be the vector in \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\) with only one non-zero component: \(\epsilon_{m}(m)=1\). **Theorem 6.4****.**: _Let \(\sigma\in X_{p}\). The representation \(\pi_{\sigma}\) as in Theorem 4.5 extends by continuity to a representation of the integral BC-algebra \({\mathcal{H}}_{\mathbb{Z}}\) on \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). For \(n\in I(p)\) and for \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), \(\pi_{\sigma}(\mu_{n})\), \(\pi_{\sigma}(x)\) and \(\pi_{\sigma}(\mu_{n}^{*})\) are \({\mathcal{O}}\)-linear operators on \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\)_ \[\pi_{\sigma}(\mu_{n})\epsilon_{m}=\epsilon_{nm},\ \ \ \ \pi_{ \sigma}(e(a/b)) \epsilon_{m}=\rho(\zeta_{a/b}^{m})\epsilon_{m}\,,\quad~{}\forall a \in{\mathbb{Z}},\ \forall b,m\in I(p)\] (62) \[\pi_{\sigma}(\mu_{n}^{*})\epsilon_{k}=\left\{\begin{array}[]{ll}0&\hbox{if}\,k \notin n{\mathbb{N}}\\ \epsilon_{k/n}&\hbox{if}\,k\in n{\mathbb{N}}\,.\end{array}\right.\] (63) _One has \(\pi_{\sigma}(x)=\pi_{\sigma}(r(x))\) for all \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) (\(r:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{({\mathbb{Q}}/{ \mathbb{Z}})^{(p)}}]\) the retraction as in (28)) and_ \[\pi_{\sigma}(\mu_{p})={\rm Fr}^{-1},\quad\pi_{\sigma}(\mu_{p}^{*})={\rm Fr}\] (64) _where \({\rm Fr}\) is the Frobenius automorphism, acting componentwise as a skew-linear operator._ Proof.: Theorem 4.5 and the density of \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) in \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\) (_cf.__e.g._[23], 1.8) show that \(\pi_{\sigma}\) extends by continuity to a representation of the integral BC-algebra \({\mathcal{H}}_{\mathbb{Z}}\) on \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). In view of the invertibility of the elements \(n\in I(p)\) in \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\), the description of the representation \(\pi_{\sigma}\) is simplified by using the elements \(\mu_{n}=\frac{1}{n}\tilde{\mu}_{n}\), to stress the analogy with the complex case. It follows from Corollary 6.3 that the subring \({\mathcal{O}}\) of \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\) is the fixed subring for the action of the operators \(F_{n}\), for all \(n\in I(p)\). For \(n\in I(p)\), the operators \(F_{n}\) are \({\mathcal{O}}\)-linear likewise the \(V_{n}\) (_cf._ Proposition 2.2, \((2)\)) which correspond to the \(\tilde{\mu}_{n}\) by means of the representation \(\pi_{\sigma}\). Thus we obtain the first equality in (62). The operators \(\pi_{\sigma}(e(a/b))\) are the multiplication operators (_cf._ Corollary 2.4) by \(\tau(e(a/b))\), thus they are \({\mathcal{O}}\)-linear and the second equation in (62) follows from (58). By applying (37) one has \(\pi_{\sigma}(\mu_{n}^{*})=F_{n}\) for all \(n\). Taking \(n=p\), one gets that \(\pi_{\sigma}(\mu_{p}^{*})=F_{p}\) which coincides with \({\rm Fr}\) acting componentwise, as it follows from the commutation \(F_{p}\circ\frac{1}{n}V_{n}=\frac{1}{n}V_{n}\circ F_{p}\) for \(n\in I(p)\) and (46). Since \(\mu_{p}^{*}\mu_{p}=1\) and \({\rm Fr}\) is invertible one gets (64). ∎ **Definition 6.5****.**: _We denote by \({\mathcal{J}}_{p}\subset{\mathcal{H}}_{\mathbb{Z}}\) the two sided ideal generated by the elements_ \[1-e(p^{-k})\,,\quad~{}\forall k\in{\mathbb{N}}.\] (65) **Proposition 6.6****.**: _One has \({\mathcal{J}}_{p}={\rm Ker}\,\pi_{\sigma}\) (cf. (62)) and the intersection \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\cap{\mathcal{J}}_{p}\) is the ideal \({\mathcal{J}}_{p}^{0}\) of \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) generated by the elements as in (65)._ _The sequence of commutative algebras_ \[0\to{\mathcal{J}}_{p}^{0}\to{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\stackrel{{ r}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{ (p)}}]\to 0\] (66) _is exact._ Proof.: Let \(r=id_{{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]}\otimes\epsilon:{ \mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{ Z}})^{(p)}}]\) be the retraction map introduced in (28). By construction, one has \[{\mathcal{J}}_{p}^{0}={\rm Ker}(r).\] (67) Since \(\pi_{\sigma}(e(a/b))\) only depends upon \(r(e(a/b))\) it follows that \({\mathcal{J}}_{p}\subset{\rm Ker}\,\pi_{\sigma}\). One knows (_cf._[15], Lemma 4.8) that any element of the algebra \({\mathcal{H}}_{\mathbb{Z}}\) can be written as a finite sum of monomials of the form \[\sum_{\{a,b\}\in{\mathbb{N}}^{2}\atop(a,b)=1}\tilde{\mu}_{a}\,x_{\{a,b\}}\,\mu _{b}^{*},\qquad x_{\{a,b\}}\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}].\] (68) We show that for any finite sum \(X\) as in (68) we have \[\pi_{\sigma}(X)=0\implies x_{\{a,b\}}\in{\mathcal{J}}_{p}^{0}.\] (69) It is enough to prove that \(r(x_{\{a,b\}})=0\), \(\forall a,b\in{\mathbb{N}}\) and since \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) is torsion free it suffices to show that \(ar(x_{\{a,b\}})=0\), \(\forall a,b\in{\mathbb{N}}\). Define \(y:{\mathbb{Q}}_{+}^{*}\to{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\), \(y(\frac{a}{b}):=a\,r(x_{\{a,b\}})\), then \(y\) has finite support. For any group homomorphism \[\chi:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{\mathcal{O}}^{\times}\] there is a unique ring homomorphism \(h_{\chi}\) with \[h_{\chi}:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathcal{O}}, \qquad h_{\chi}(e(\gamma))=\chi(\gamma)\,,\quad~{}\forall\gamma\in{({\mathbb{Q }}/{\mathbb{Z}})^{(p)}}.\] (70) This applies in particular, for any integer \(j\), to \(\chi=\rho^{j}\) where we view \(\rho:{\mathbb{Q}}^{\rm cyc,p}\to{\mathbb{C}}_{p}\) as a group homomorphism \(\rho:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{\mathcal{O}}^{\times}\). One has \[\bigcap_{j\in{\mathbb{Z}}}\,{\rm Ker}\,h_{\rho^{j}}=\{0\}\] (71) since an injective character of a finite cyclic group generates the dual group. Let \(n,m\in I(p)\) be relatively prime. Then one has for any \(j\in I(p)\) and \(z\in{\mathcal{O}}\) \[(\pi_{\sigma}(X)z\epsilon_{jm})_{jn}=\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{ -k}\frac{n}{m}))\,{\rm Fr}^{k}(z).\] (72) Thus if \(\pi_{\sigma}(X)=0\) one has for all \(j\) and \(m,n\) as above \[\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))\,{\rm Fr}^{k}(z)=0 \qquad\forall z\in{\mathcal{O}}.\] (73) For \(z\) a root of unity one has \({\rm Fr}^{k}(z)=z^{p^{k}}\), thus the polynomial \[\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))\,Z^{p^{k+n}}\] vanishes, for \(n\) large enough, on all roots of unity thus it is identically zero, hence all its coefficients must vanish _i.e._ \[h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))=0\,,\quad~{}\forall k\in{\mathbb{Z}},\ j\in {\mathbb{N}}.\] (74) It then follows from (71) that \(y(\frac{a}{b})=y(p^{-k}\frac{n}{m})=0\), hence (69) holds and the proof that any element of \({\rm Ker}\,\pi_{\sigma}\) is in \({\mathcal{J}}_{p}\) is complete. Finally, if \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) belongs to \({\rm Ker}\,\pi_{\sigma}\) one has \(x\in{\mathcal{J}}_{p}^{0}\) by (69) and thus the intersection \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\cap{\mathcal{J}}_{p}\) is the ideal \({\mathcal{J}}_{p}^{0}\).∎ **Definition 6.7****.**: _We denote by \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) the quotient by \({\mathcal{J}}_{p}\) of the subalgebra of \({\mathcal{H}}_{\mathbb{Z}}\) generated by \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), \(\tilde{\mu}_{n}\), \(\mu_{n}^{*}\), for \(n\in I(p)\)._ The algebra \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) is generated by \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) the operators \(\tilde{\mu}_{n}\) and \(\mu_{n}^{*}\), for \(n\in I(p)\) and its presentation is similar to the presentation of \({\mathcal{H}}_{\mathbb{Z}}\). The relations are \[\begin{array}[]{l}\tilde{\mu}_{nm}=\tilde{\mu}_{n}\tilde{\mu}_{m}\,,\ \mu_{nm} ^{*}=\mu_{n}^{*}\mu_{m}^{*}\,,\quad~{}\forall n,m\in I(p)\\[8.535827pt] \mu_{n}^{*}\tilde{\mu}_{n}=n\,,\quad~{}\forall n\in I(p)\\[8.535827pt] \tilde{\mu}_{n}\mu_{m}^{*}=\mu_{m}^{*}\tilde{\mu}_{n}\,,\quad~{}\forall n,m\in I (p)\quad\text{with}~{}(n,m)=1\end{array}\] (75) as well as the relations \[\begin{array}[]{l}\tilde{\mu}_{n}x\mu_{n}^{*}=\tilde{\rho}_{n}(x)\,,\ \mu_{n}^ {*}x=\sigma_{n}(x)\mu_{n}^{*}\,,\ x\tilde{\mu}_{n}=\tilde{\mu}_{n}\sigma_{n}(x )\end{array}\] (76) where \(\tilde{\rho}_{n}\), \(n\in I(p)\) is defined by \[\tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{\prime}=\gamma}e(\gamma^{\prime})\, ,\quad~{}\forall\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (77) Given an algebra \({\mathcal{A}}\), an automorphism \(\theta\in{\rm Aut}({\mathcal{A}})\) and an integer \(p\) we let \({\mathcal{A}}\rtimes_{\theta,\,p}{\mathbb{Z}}\) be the subalgebra of the algebraic cross product \(\{{\sum_{n\in{\mathbb{Z}}}}a_{n}V^{n}\mid a_{n}\in{\mathcal{A}}\}\) determined by the condition \[a_{-n}\in p^{n}{\mathcal{A}}\,,\quad~{}\forall n\in{\mathbb{N}}.\] (78) If we let \(V=U^{*}\) and \(pV^{-1}=\tilde{U}\), then it is easy to see that \({\mathcal{A}}\rtimes_{\theta,\,p}{\mathbb{Z}}\) is generated by \({\mathcal{A}},\tilde{U},U^{*}\) with the relations \[U^{*}\tilde{U}=p,\ \tilde{U}xU^{*}=p\theta^{-1}(x)\,,\ U^{*}x=\theta(x)U^{*}\, ,\ x\tilde{U}=\tilde{U}\theta(x)\,,\quad~{}\forall x\in{\mathcal{A}}.\] (79) **Proposition 6.8****.**: _There exists a unique automorphism \({\rm Fr}\in{\rm Aut}({\mathcal{H}}_{\mathbb{Z}}^{(p)})\) such that_ \[{\rm Fr}(e(\gamma))=e(\gamma)^{p}\,,\quad~{}\forall\gamma\in{({\mathbb{Q}}/{ \mathbb{Z}})^{(p)}}\,,\ {\rm Fr}(\tilde{\mu}_{n})=\tilde{\mu}_{n}\,,\ {\rm Fr} (\mu_{n}^{*})=\mu_{n}^{*}\,,\quad~{}\forall n\in I(p).\] (80) _One derives an isomorphism_ \[{\mathcal{H}}_{\mathbb{Z}}/{\mathcal{J}}_{p}={\mathcal{H}}_{\mathbb{Z}}^{(p)} \rtimes_{{\rm Fr},\,p}{\mathbb{Z}}.\] (81) Proof.: The map \(\gamma\to p\gamma\) defines an automorphism of \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Its linearization \({\rm Fr}\) acts on \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) and commutes with the endomorphisms \(\sigma_{n}\) and \(\tilde{\rho}_{n}\). In fact by applying the isomorphism of Proposition 4.4, \({\rm Fr}\) corresponds to the Frobenius automorphism of \(\bar{\mathbb{F}}_{p}\). Thus it extends to an automorphism \({\rm Fr}\in{\rm Aut}({\mathcal{H}}_{\mathbb{Z}}^{(p)})\). The second statement follows by comparing the presentation of \({\mathcal{H}}_{\mathbb{Z}}/{\mathcal{J}}_{p}\) with that of the crossed product \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\rtimes_{{\rm Fr},\,p}{\mathbb{Z}}\) as in (79). ∎ **Proposition 6.9****.**: _Let \(\sigma\in X_{p}\)._ \((1)\) _The restriction \(\pi_{\sigma}|_{{\mathcal{H}}_{\mathbb{Z}}^{(p)}}\) of the representation \(\pi_{\sigma}\) (as in Theorem 6.4) to \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) is \({\mathcal{O}}\)-linear and indecomposable over \({\mathcal{O}}\)._ \((2)\) _The representations \(\pi_{\sigma}|_{{\mathcal{H}}_{\mathbb{Z}}^{(p)}}\) are pairwise inequivalent._ \((3)\) _The representation \(\pi_{\sigma}\) is linear and indecomposable over \({\mathbb{Z}}_{p}\)._ \((4)\) _Two representations \(\pi_{\sigma}\) and \(\pi_{\sigma^{\prime}}\) are equivalent over \({\mathbb{Z}}_{p}\) if and only if there exists \(\alpha\in{\rm Aut}(\bar{\mathbb{F}}_{p})\) such that \(\sigma^{\prime}=\sigma\circ\alpha\)._ Proof.: \((1)\) The \({\mathcal{O}}\)-linearity property is checked directly on the generators using Theorem 6.4. It follows from (62) that the vector \(\epsilon_{1}\) is cyclic for \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\), _i.e._\(\pi_{\sigma}({\mathcal{H}}_{\mathbb{Z}}^{(p)})\,\epsilon_{1}\) is dense in \({\mathbb{W}}(\bar{\mathbb{F}}_{p})={\mathcal{O}}^{I(p)}\). One has \[{\mathcal{O}}\epsilon_{1}=\{\xi\in{\mathbb{W}}(\bar{\mathbb{F}}_{p})\mid\pi_{ \sigma}(\mu_{n}^{*})(\xi)=0\,,\quad~{}\forall n\neq 1,\ n\in I(p)\}.\] (82) For any \({\mathcal{O}}\)-linear continuous operator \(T\) in the commutant of \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) one has \(\pi_{\sigma}(\mu_{n}^{*})T\epsilon_{1}=T\pi_{\sigma}(\mu_{n}^{*})\epsilon_{1}=0\), \(\forall n>1\) and by (82) there exists \(\lambda\in{\mathcal{O}}\) such that \(T\epsilon_{1}=\lambda\epsilon_{1}\). Thus since \(\epsilon_{1}\) is cyclic, \(T\) is given by the module action of \(\lambda\in{\mathcal{O}}\). \((2)\) By (62), the action of \(\pi_{\sigma}(e(\gamma))\) for \(\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) on the subspace (82) is given by the multiplication by \(\rho(\gamma)\in{\mathcal{O}}\). Thus \(\rho\) is an invariant of the representation. \((3)\) Any element of the commutant of the action of \({\mathcal{H}}_{\mathbb{Z}}\) is given by the module action of \(\lambda\in{\mathcal{O}}\), where \(\lambda\) is fixed for the action of the Frobenius on \({\mathcal{O}}\), _i.e._\(\lambda\in{\mathbb{Z}}_{p}\). This shows that \(\pi_{\sigma}\) is indecomposable. \((4)\) We show first that if there exists \(\alpha\in{\rm Aut}(\bar{\mathbb{F}}_{p})\) such that \(\sigma^{\prime}=\sigma\circ\alpha^{-1}\), the representations \(\pi_{\sigma}\) and \(\pi_{\sigma^{\prime}}\) are equivalent over \({\mathbb{Z}}_{p}\). Let \(\tilde{\alpha}={\mathbb{W}}_{p^{\infty}}(\alpha)\in{\rm Aut}({\mathbb{W}}_{p^{ \infty}}(\bar{\mathbb{F}}_{p}))={\rm Aut}({\mathcal{O}})\) and define \(U:{\mathcal{O}}^{I(p)}\to{\mathcal{O}}^{I(p)}\,,\ \ (U\xi)_{n}=\tilde{\alpha}( \xi_{n})\,,\quad~{}\forall n\in I(p)\). One has \(U\epsilon_{n}=\epsilon_{n}\) for all \(n\in I(p)\) and if \(T\) is an \({\mathcal{O}}\)-linear operator so is \(UTU^{-1}\). It thus follows from (62) and (63) that \(U\pi_{\sigma}(\mu_{n})U^{-1}=\pi_{\sigma}(\mu_{n})\) and \(U\pi_{\sigma}(\mu_{n}^{*})U^{-1}=\pi_{\sigma}(\mu_{n}^{*})\). For \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), \(U\pi_{\sigma}(x)U^{-1}\) only depends on \(r(x)\) and for \(x=e(a/b)\), \(b\in I(p)\), one has \(U\pi_{\sigma}(e(a/b))U^{-1}\epsilon_{m}=\tilde{\alpha}(\rho(\zeta_{a/b}^{m})) \epsilon_{m}=\rho^{\prime}(\zeta_{a/b}^{m})\epsilon_{m}=\pi_{\sigma^{\prime}}( e(a/b))\). Moreover since \(\tilde{\alpha}\) commutes with \({\rm Fr}\), it follows from (64) that \(U\pi_{\sigma}(\mu_{p})U^{-1}=\pi_{\sigma}(\mu_{p})\) and \(U\pi_{\sigma}(\mu_{p}^{*})U^{-1}=\pi_{\sigma}(\mu_{p}^{*})\). Thus one gets the required equivalence. Conversely, assume that two representations \(\pi_{\sigma}\) and \(\pi_{\sigma^{\prime}}\) are equivalent over \({\mathbb{Z}}_{p}\). By (82) the \({\mathbb{Z}}_{p}\)-linear representation \(\pi_{\sigma}\) (and similarly \(\pi_{\sigma^{\prime}}\)) determines uniquely the following representation of \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) in the \({\mathbb{Z}}_{p}\)-module \({\mathcal{O}}\) \[\beta_{\sigma}(e(a/b))\xi=\rho(\zeta_{a/b})\xi\,,\quad~{}\forall\xi\in{ \mathcal{O}}.\] (83) In turns this determines an extension of the \(p\)-adic valuation to the subfield \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) generated over \({\mathbb{Q}}\) by \(\mu^{(p)}\). Indeed the formula \[{\rm val}(x)=\inf\{k\geq 0\mid\beta_{\sigma}(x){\mathcal{O}}\subset p^{k}{ \mathcal{O}}\}\,,\quad~{}\forall x\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}}) ^{(p)}}]\] (84) only depends on the class of \(x\) in \({\mathbb{Q}}^{\rm cyc,p}\) and extends uniquely to a valuation on \({\mathbb{Q}}^{\rm cyc,p}\). The conclusion then follows from Proposition 8.14. ∎ ## 7. The KMS theory of the BC-system at a prime \(p\) In [4] it was shown that the extremal, complex KMS states below critical temperature of the BC-system (_cf._ (24)) are of the form \[\varphi_{\beta,\rho}(X)=\frac{{\rm Tr}(\pi_{\rho}(X)e^{-\beta H})}{{\rm Tr}(e^ {-\beta H})}\,,\quad~{}\forall X\in{\mathcal{H}}_{\mathbb{Z}}\] (85) where \(H\) is the Hamiltonian operator of multiplication by \(\log n\) in the canonical basis \(\epsilon_{n}\) of the Hilbert space \(\ell^{2}({\mathbb{N}})\) and \(\pi_{\rho}\) is the irreducible representation of the algebra \({\mathcal{H}}_{\mathbb{Q}}\) given by \[\pi_{\rho}(\mu_{n})\epsilon_{m}=\epsilon_{nm},\ \ \pi_{\rho}(\mu_{n}^{*})=\pi_ {\rho}(\mu_{n})^{*}\,,\ \ \pi_{\rho}(e(a/b))\epsilon_{m}=\rho(\zeta_{a/b}^{m}) \epsilon_{m},\] (86) where \(\rho\in\hat{\mathbb{Z}}^{*}\) determines an embedding in \({\mathbb{C}}\) of the cyclotomic field \({{\mathbb{Q}}^{\rm cyc}}\) generated by the abstract roots of unity. Thus the extremal KMS states \(\varphi_{\beta,\rho}\) are directly computable using the representation \(\pi_{\rho}\) and the explicit description of the Hamiltonian. In section 6, we have described the \(p\)-adic analogue of the representation \(\pi_{\rho}\). In this section, our goal is to obtain the \(p\)-adic analogue of the KMS states \(\varphi_{\beta,\rho}\). The guiding equation is provided by the general algebraic formulation of the KMS condition which is described by the equality \[\varphi(x\sigma(y))=\varphi(y\,x)\,,\quad~{}\forall x,y\in{\mathcal{A}},\] (87) where \(\varphi\) is a linear form on an algebra \({\mathcal{A}}\) endowed with an automorphism \(\sigma\in{\rm Aut}({\mathcal{A}})\). In our case the algebra is \[{\mathcal{A}}={\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}={\mathcal{H}}_{\mathbb{Z} }^{(p)}\otimes_{\mathbb{Z}}{\mathbb{C}}_{p}.\] (88) In §7.1 we introduce, using the Iwasawa logarithm as a substitute for the above complex Hamiltonian \(H\), the automorphisms \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\). These automorphisms are defined for \(\beta\) in the “extended \(s\)-disk” \(D_{p}\) (_cf._ (91) below). In §7.5 we shall show how to extend their definition from the domain \(D_{p}\) to a covering \(M\) of \({\mathbb{C}}_{p}\). The construction of the KMS states is based on the classical construction of the \(p\)-adic L-functions and \(p\)-adic polylogarithm and many properties that we obtain rely on the simplifications which occur when \(\beta=1-k(p-1)\) (\(k\in{\mathbb{Z}}\)). In §7.2 we prove the identities in the cyclotomic field, involving Bernoulli polynomials, which are behind the verification of the KMS condition. In §7.3 we provide the construction of the linear forms \(\varphi_{\beta,\rho}\) using some of the results from [37] (_cf._ Chapter V). In §7.4 we prove that the functionals \(\varphi_{\beta,\rho}\) fulfill the KMS condition with respect to the automorphism \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\). Unlike the complex case, this construction exhibits the (new) phenomenon of the invariance of the linear forms \(\varphi_{\beta,\rho}\) under the symmetry of \({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\) given by the automorphism \(e(\gamma)\mapsto e(-\gamma)\). Throughout this section we fix a finite, rational prime \(p\) and an algebraic closure \(\bar{\mathbb{Q}}_{p}\) whose completion is denoted \({\mathbb{C}}_{p}\). We also use the following notation \[q=4,\ \text{if}\ p=2,\qquad q=p,\ \text{if}\ p\neq 2\,.\] (89) and \[\varphi(q)=2,\ \text{if}\ p=2,\qquad\varphi(q)=p-1,\ \text{if}\ p\neq 2\,.\] (90) We consider the “extended \(s\)-disk” \[D_{p}:=\{\beta\in{\mathbb{C}}_{p}\mid|\beta|_{p}<qp^{-1/(p-1)}>1\}\,,\ \\] (91) and first develop the theory for \(\beta\in D_{p}\). In §7.5 we shall explain how the Iwasawa construction of \(p\)-adic \(L\)-functions allows one to extend the whole theory from the domain \(D_{p}\) to the covering of \({\mathbb{C}}_{p}\) given by the multiplicative group \(M\) which is the open disk of radius one and center \(1\) in \({\mathbb{C}}_{p}\). ### The automorphisms \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) Let \({\mathbb{Z}}_{(p)}^{\times}\subset{\mathbb{Q}}^{\times}\) be the multiplicative group of rational fractions whose numerator and denominator are prime to \(p\). **Lemma 7.1****.**: _Let \(r\in{\mathbb{Z}}_{(p)}^{\times}\). There exists a unique analytic function_ \[D_{p}\to{\mathbb{C}}_{p},\quad\beta\mapsto r^{(\beta)}\] (92) _such that_ \[r^{(\beta)}=r^{\beta}\,,\quad~{}\forall\beta=1-k\varphi(q).\] (93) Proof.: We recall that the Iwasawa logarithm \(\log_{p}\) is the unique extension of the function defined in the open unit disk centered at \(1\) by \[-\log_{p}(1-x)=\sum_{n=1}^{\infty}\frac{x^{n}}{n}\,,\quad~{}\forall x\in{ \mathbb{C}}_{p},\ |x|_{p}<1\] (94) to a map \(\log_{p}:{\mathbb{C}}_{p}^{\times}\to{\mathbb{C}}_{p}\) such that \[\log_{p}(xy)=\log_{p}(x)+\log_{p}(y)\,,\quad~{}\forall x,y\in{\mathbb{C}}_{p} \,,\ \ \log_{p}(p)=0\,.\] (95) One has \(\log_{p}(-1)=0\) since \(-1\) is a root of unity, and \[|\log_{p}(r)|_{p}\leq q^{-1}\,,\quad~{}\forall r\in{\mathbb{Z}}_{(p)}^{\times}.\] (96) Moreover the exponential function is defined by the series \[{\rm exp}(x)=\sum_{n=1}^{\infty}\frac{x^{n}}{n!}\,,\quad~{}\forall x\in{ \mathbb{C}}_{p}\,,\ |x|_{p}<r_{p}=p^{-\frac{1}{p-1}}.\] (97) We define \[r^{(\beta)}:=r\,{\rm exp}((\beta-1)\log_{p}(r))\,,\quad~{}\forall\beta\in D_{p}.\] (98) This is a well-defined, analytic function of \(\beta\in D_{p}\) since \(\beta-1\in D_{p}\) and thus \(|(\beta-1)\log_{p}(r)|_{p}<r_{p}\) by (96). We show that (93) holds. This follows from the equality \[{\rm exp}(k\varphi(q)\log_{p}(r))=r^{k\varphi(q)}\,,\quad~{}\forall r\in{ \mathbb{Z}}_{(p)}^{\times},\ k\in{\mathbb{Z}}\] which holds for \(r=-1\) since \(\varphi(q)\) is even. In general, (93) follows from the formula \[{\rm exp}(n\log_{p}(a))=a^{n}\,,\quad~{}\forall a\in{\mathbb{Z}}_{p}^{*}\,,\ n \in\varphi(q){\mathbb{Z}}\] (99) as shown in [37] (Chapter 5, p. 52), where the notation \[\langle a\rangle={\rm exp}(\log_{p}(a))\] (100) is introduced. The uniqueness follows from the discreteness of the set of zeros of analytic functions. ∎ **Lemma 7.2****.**: _Let \(\beta\in D_{p}\), then_ \[{\mathbb{Z}}_{(p)}^{\times}\ni r\mapsto r^{(\beta)}\in{\mathbb{C}}_{p}^{\times}\] (101) _is a group homomorphism. Moreover, for \(r\in{\mathbb{Z}}_{(p)}^{\times}\)_ \[r^{(\beta_{1})}r^{(\beta_{2})}=r^{(\beta_{1}+\beta_{2})}r^{(0)}\,,\quad~{} \forall\beta_{j}\in D_{p}\] (102) Proof.: This follows from (95) and the equality (_cf._[32]) \[{\rm exp}(x_{1}+x_{2})={\rm exp}(x_{1}){\rm exp}(x_{2})\,,\quad~{}\forall x_{j },\ |x_{j}|_{p}<r_{p}.\] (103) ∎ The standard notation for \(r^{(0)}\) is \(\omega(r)\): it is the unique \(\varphi(q)\) root of unity which is congruent to \(r\) modulo \(q\). In particular one has \[(r^{(0)})^{\varphi(q)}=1\,,\quad~{}\forall r\in{\mathbb{Z}}_{(p)}^{\times}.\] (104) **Proposition 7.3****.**: \((1)\) _For \(\beta\in D_{p}\) there exists a unique automorphism \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) such that_ \[\sigma^{(\beta)}(\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*})=\left(\frac{b}{a}\right) ^{(\beta)}\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*}\,,\quad~{}\forall a,b\in I(p),\ \gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (105) \((2)\) _One has_ \[\sigma^{(\beta_{1})}\circ\sigma^{(\beta_{2})}=\sigma^{(\beta_{1}+\beta_{2})} \circ\sigma^{(0)}\,,\quad~{}\forall\beta_{j}\in D_{p}\] (106) _and \(\sigma^{(0)}\) is an automorphism of order \(\varphi(q)\)._ Proof.: It suffices to check that \(\sigma^{(\beta)}\) preserves the presentation given by the relations (75) and (76). This follows from the multiplicativity shown in Lemma 7.2. Similarly (106) follows from (102). The last statement follows from (104).∎ ### Cyclotomic identities for the polylogarithm We recall that the Bernoulli polynomials \(B_{n}(u)\) are defined inductively as follows \[B_{0}(x)=1\,,\ \ B^{\prime}_{n}(x)=nB_{n-1}(x)\,,\ \ \int_{0}^{1}B_{n}(x)dx=0.\] Equivalently, these polynomials can be introduced using the generating function \[F(u,t)=\frac{te^{ut}}{e^{t}-1}=\sum_{n=0}^{\infty}B_{n}(u)\frac{t^{n}}{n!}.\] (107) The first few are \[B_{0}(u) = 1\] \[B_{1}(u) = -\frac{1}{2}+u\] \[B_{2}(u) = \frac{1}{6}-u+u^{2}\] \[B_{3}(u) = \frac{u}{2}-\frac{3u^{2}}{2}+u^{3}\] \[B_{4}(u) = -\frac{1}{30}+u^{2}-2u^{3}+u^{4}\] \[B_{5}(u) = -\frac{u}{6}+\frac{5u^{3}}{3}-\frac{5u^{4}}{2}+u^{5}.\] These polynomials fulfill the equation \(B_{n}(1-u)=(-1)^{n}B_{n}(u)\). The Bernoulli numbers are \(B_{n}=B_{n}(0)\). Using (107), one checks the identity (_cf._[37], Chapter 4, Proposition 4.1) \[g^{n-1}\sum_{j=0}^{g-1}B_{n}(\frac{x+j}{g})=B_{n}(x)\,.\] (108) We also introduce inductively the rational fractions \(\ell_{\beta}(z)\) for \(\beta\in-{\mathbb{N}}\), as follows \[z\partial_{z}\ell_{\beta}(z)=\ell_{\beta-1}(z)\,,\ \ell_{0}(z)=\frac{z}{1-z}.\] (109) For \(\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\) we denote by \(\zeta_{\alpha}\in{{\mathbb{Q}}^{\rm cyc}}\) the class of \(e(\alpha)\in{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) modulo the cyclotomic ideal (_cf._ Definition 8.1). It is a root of unity whose order is the denominator of \(\alpha\). **Lemma 7.4****.**: _Let \(n>1\), \(a,b\in{\mathbb{N}}\). Then_ \[b^{n-1}\sum_{j=0}^{b-1}\zeta_{a/b}^{j}B_{n}(\frac{j}{b})=\left\{\begin{array}[ ]{ll}-n\ell_{1-n}(\zeta_{a/b}),&\hbox{if}\ \zeta_{a/b}\neq 1\\ B_{n},&\hbox{if}\ \zeta_{a/b}=1.\end{array}\right.\] (110) Proof.: The equality (110) for \(\zeta_{a/b}=1\) follows from (108). Thus we can assume that \(z=\zeta_{a/b}\neq 1\). The Taylor expansion at \(t=0\) of \((ze^{t}-1)^{-1}\) is given by \[(ze^{t}-1)^{-1}=(z-1)^{-1}-\sum_{n=1}^{\infty}\ell_{-n}(z)\frac{t^{n}}{n!}\] (111) since \((z-1)^{-1}=-1-\ell_{0}(z)\) and \(\partial_{t}\) agrees with \(z\partial_{z}\). Then for \(b\in{\mathbb{N}}\) and \(t\) such that \(ze^{\frac{t}{b}}\neq 1\) one has \[\sum_{j=0}^{b-1}z^{j}e^{\frac{j}{b}t}=\frac{z^{b}e^{t}-1}{ze^{\frac{t}{b}}-1}.\] Since \(z^{b}=1\), one derives \[\sum_{n=0}^{\infty}\left(\sum_{j=0}^{b-1}z^{j}B_{n}(\frac{j}{b})\right)\frac{t ^{n}}{n!}=\sum_{j=0}^{b-1}z^{j}F(\frac{j}{b},t)=\frac{t}{ze^{\frac{t}{b}}-1}.\] Since \(z\neq 1\), taking the Taylor expansion at \(t=0\) using (111), gives the equality \[\sum_{j=0}^{b-1}z^{j}B_{n}(\frac{j}{b})=-\frac{n}{b^{n-1}}\ell_{1-n}(z),\qquad \forall n>1\,.\] (112) ∎ **Proposition 7.5****.**: _Let \(n>1\), \(a,b\in{\mathbb{N}}\)._ \((1)\) _The following sum only depends upon \(n\) and \(\frac{a}{b}\in{\mathbb{Q}}/{\mathbb{Z}}\)_ \[Y_{n}(a/b)=f^{n-1}\sum_{j=0}^{f-1}\zeta_{a/b}^{j}B_{n}(\frac{j}{f})\,,\quad~{} \forall f\in b{\mathbb{N}},\ f\neq 0.\] (113) \((2)\) _One has_ \[\frac{1}{b}\sum_{a=0}^{b-1}Y_{n}(a/b)=b^{n-1}B_{n}=b^{n-1}Y_{n}(0).\] (114) \((3)\) _For \(g\geq 1\), \(x^{g}\neq 1\) one has_ \[\frac{1}{g}\sum_{j=0}^{g-1}\ell_{1-n}(\zeta_{j/g}\,x)=g^{n-1}\ell_{1-n}(x^{g}).\] (115) Proof.: \((1)\) Follows from (110). To obtain \((2)\), note that \[\frac{1}{b}\sum_{a=0}^{b-1}\zeta_{a/b}^{j}=0\,,\quad~{}\forall j\neq 0\ (b)\,, \ \ \frac{1}{b}\sum_{a=0}^{b-1}\zeta_{a/b}^{j}=1\,,\quad~{}\forall j=0\ (b).\] \((3)\) One checks (115) as an identity between rational fractions by induction on \(n\in{\mathbb{N}}\). It holds for \(n=1\) by applying the operation \(-z\partial_{z}\log()\) to both sides of the identity \[\prod_{j=0}^{g-1}(1-\zeta_{j/g}z)=1-z^{g}.\] To obtain (115) for \(n\) assuming it for \(n-1\) one applies the operation \(z\partial_{z}\) to both sides of the identity for \(n-1\). ∎ Combining (115) with (110) we obtain, using (114) when \(\alpha\in{\mathbb{Z}}\) \[\frac{1}{b}\sum_{j=0}^{b-1}Y_{n}(\frac{\alpha+j}{b})=b^{n-1}Y_{n}(\alpha)\,, \quad~{}\forall\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\] (116) ### The linear forms \(\varphi_{\beta,\rho}\) In this section we shall provide a meaning to expressions of the form \[Z_{\rho}(\frac{a}{b},\beta)=\sum_{m\in I(p)}\rho(\zeta_{a/b}^{m})\,m^{-\beta}, \qquad\beta\in D_{p}\] (117) where \(\frac{a}{b}\in{\mathbb{Q}}\), \(b\in I(p)\) is an integer prime to \(p\) and \(\rho:{{\mathbb{Q}}^{\rm cyc}}\hookrightarrow{\mathbb{C}}_{p}\). Note that as a function of \(m\in I(p)\), \(\rho(\zeta_{a/b}^{m})\) only depends on the residue of \(m\) modulo \(b\). We let \(f=bp\) and decompose the sum (117) according to the residue \(\alpha\) of \(m\) modulo \(f\). One has \({\mathbb{Z}}/f{\mathbb{Z}}={\mathbb{Z}}/p{\mathbb{Z}}\times{\mathbb{Z}}/b{ \mathbb{Z}}\). The elements of \(I(p)\) are characterized by the fact that their residues mod. \(f\) are given by pairs \(\alpha=(\alpha_{1},\alpha_{2})\in{\mathbb{Z}}/f{\mathbb{Z}}\), with \(\alpha_{1}\neq 0\). For \(\alpha\in({\mathbb{Z}}/p{\mathbb{Z}})^{\times}\times{\mathbb{Z}}/b{\mathbb{Z}}\), we let \(\tilde{\alpha}\in{\mathbb{N}}\) be the smallest integer with residue modulo \(f\) equal to \(\alpha\). Then, the sum (117) can be written as \[Z_{\rho}(\frac{a}{b},\beta)=\sum_{\alpha}\rho(\zeta_{a/b}^{\alpha})\,\sum_{n \geq 0}(\tilde{\alpha}+fn)^{-\beta},\qquad\beta\in D_{p}.\] (118) Notice that the first sum (over \(\alpha\)) in (118) only involves finitely many terms. Each infinite sum in (118) is of the form (with \(z=\tilde{\alpha}/f\)) \[\sum_{n\in{\mathbb{N}}}(\tilde{\alpha}+fn)^{-\beta}=f^{-\beta}\,\sum_{n\in{ \mathbb{N}}}(z+n)^{-\beta},\qquad\beta\in D_{p}\] (119) and it is well known that this expression retains a meaning in the \(p\)-adic context (_cf._[37] Chapter V). More precisely, the asymptotic expansion in the complex case, for \(z\to\infty\) (this process goes back to Euler’s computation of \(\sum_{1}^{\infty}n^{-2}\)) \[\sum_{n=0}^{\infty}(z+n)^{-\beta}\sim\frac{z^{1-\beta}}{\beta-1}\sum_{0}^{ \infty}\binom{1-\beta}{j}B_{j}z^{-j}\] motivates the following precise formula, where we prefer to leave some freedom in the choice of the multiple \(f\) of \(bq\). **Lemma 7.6****.**: _With \(q\) as in (91), and \(f\in{\mathbb{N}}\), \(f\neq 0\), a multiple of \(bq\), the expression_ \[Z_{\rho}(\frac{a}{b},\beta,f):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{ \mathbb{N}}}\rho(\zeta_{a/b}^{c})\,\frac{\langle c\rangle^{1-\beta}}{\beta-1} \sum_{j=0}^{\infty}\binom{1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j},\qquad \beta\in D_{p},\] (120) _defines a meromorphic function of \(\beta\in D_{p}\) with a single pole at \(\beta=1\)._ Proof.: It follows from [37] (Proposition 5.8) and the inequality (_cf._[37] Theorem 5.10) \[|\left(\frac{f}{c}\right)^{j}B_{j}|_{p}\leq p|f|_{p}^{j}\] that the series \[\sum_{j=0}^{\infty}\binom{1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j}\] converges for \(|\beta|_{p}<|f|_{p}^{-1}p^{-\frac{1}{p-1}}\geq qp^{-\frac{1}{p-1}}>1\).∎ **Lemma 7.7****.**: _For \(\beta\) a negative odd integer of the form \(\beta=1-m=1-k\varphi(q)\), and \(f\in{\mathbb{N}}\), \(f\neq 0\), \(f\) a multiple of \(bq\), one has, with \(Y_{m}\) defined by (113)_ \[Z_{\rho}(\frac{a}{b},\beta,f)=-\frac{1}{m}\rho\left(Y_{m}\left(\frac{a}{b} \right)-p^{m-1}Y_{m}\left(\frac{pa}{b}\right)\right)\,.\] (121) Proof.: For \(1\leq c<f\), \(c\notin p{\mathbb{N}}\), one has \(\langle c\rangle^{1-\beta}=c^{m}\). The binomial coefficients \(\binom{1-\beta}{j}\) in (120) all vanish for \(j>m\) and the sum defining \(Z(\frac{a}{b},\beta,f)\) is therefore finite. One has \[\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1-\beta}{j }\left(\frac{f}{c}\right)^{j}B_{j}=-\frac{c^{m}}{m}\sum_{j=0}^{m}\binom{m}{j} \left(\frac{f}{c}\right)^{j}B_{j}.\] Moreover for any integer \(m>0\), the Bernoulli polynomials fulfill the equation \[\sum_{j=0}^{m}\binom{m}{j}z^{-j}B_{j}=z^{-m}B_{m}(z)\,.\] For \(1\leq c<f\), \(c\notin p{\mathbb{N}}\), one thus gets, taking \(z=\frac{c}{f}\) \[\frac{1}{f}\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom {1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j}=-\frac{f^{m-1}}{m}B_{m}\left( \frac{c}{f}\right)\,.\] (122) One defines for any \(c\in{\mathbb{N}}\) \[T(c):=-\frac{f^{m-1}}{m}B_{m}\left(\frac{c}{f}\right).\] (123) One has \[Z_{\rho}(\frac{a}{b},\beta,f)=\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}T(c) \rho(\zeta_{a/b}^{c})=\sum_{0\leq c<f}T(c)\rho(\zeta_{a/b}^{c})-\sum_{c=jp \atop 0\leq j<f/p}T(c)\rho(\zeta_{a/b}^{c}).\] Since \(b\) divides \(f\), one derives \[\sum_{0\leq c<f}T(c)\rho(\zeta_{a/b}^{c})=-\frac{f^{m-1}}{m}\sum_{0\leq c<f} \rho(\zeta_{a/b}^{c})B_{m}\left(\frac{c}{f}\right)=-\frac{1}{m}\rho(Y_{m}( \zeta_{a/b}))\] while, since \(b\) divides \(f/p=f^{\prime}\) one gets \[\sum_{c=jp\atop 0\leq j<f/p}T(c)\rho(\zeta_{a/b}^{c})=-\frac{f^{m-1}}{m}\sum_{ 0\leq j<f/p}\rho(\zeta_{a/b}^{jp})B_{m}\left(\frac{j}{f^{\prime}}\right)=- \frac{p^{m-1}}{m}\rho(Y_{m}(\zeta_{a/b}^{p})).\] The equality (121) follows.∎ **Corollary 7.8****.**: _The function_ \[Z_{\rho}(\frac{a}{b},\beta):=Z_{\rho}(\frac{a}{b},\beta,f)\] (124) _is independent of the choice of \(f\in bq{\mathbb{N}}\), \(f\neq 0\)._ Proof.: For two choices \(f,f^{\prime}\) the analytic function of \(\beta\in D_{p}\) \[(\beta-1)(Z_{\rho}(\frac{a}{b},\beta,f)-Z_{\rho}(\frac{a}{b},\beta,f^{\prime}))\] vanishes at all negative integers \(1-k\varphi(q)\) by the equality (121), thus it is identically \(0\).∎ **Definition 7.9****.**: _The following equation defines a linear form \(\varphi_{\beta,\rho}\) on \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) for any \(\beta\in D_{p}\)_ \[\varphi_{\beta,\rho}(\tilde{\mu}_{n}e(\frac{a}{b})\mu_{m}^{*})=\left\{\begin{ array}[]{ll}Z_{\rho}(\frac{a}{b},\beta)&\hbox{if}\ n=m=1\,,\\ 0&\hbox{otherwise,}\end{array}\right.\] (125) _for \(n,m\in I(p)\) relatively prime._ The next lemma will play an important role in the proof (_cf._ next section) that \(\varphi_{\beta,\rho}\) fulfills the KMS condition. **Lemma 7.10****.**: _For any \(n\in I(p)\) and \(\beta\in D_{p}\), \(\beta\neq 1\), one has_ \[\varphi_{\beta,\rho}(\tilde{\rho}_{n}(X))=\langle n\rangle^{1-\beta}\varphi_{ \beta,\rho}(X)\,,\quad~{}\forall X\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}}) ^{(p)}}]\] (126) _(cf. (77) for the definition of \(\tilde{\rho}_{n}\))._ Proof.: After multiplication by \(\beta-1\), both sides of (126) are analytic functions of \(\beta\in D_{p}\). Thus it is enough to show that (126) holds for \(\beta=1-k\varphi(q)=1-m\). In this case one has \(\langle n\rangle^{1-\beta}=n^{m}\) and, from (121) one gets \[\varphi_{\beta,\rho}(e(\gamma))=-\frac{1}{m}\rho\left(Y_{m}(\gamma)-p^{m-1}Y_{ m}(p\gamma)\right)\,,\quad~{}\forall\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p) }}.\] To prove the equality (126) we can assume that \(X=e(\alpha)\) for \(\alpha\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). One has \[\tilde{\rho}_{n}(X)=\sum_{j=0}^{n-1}e(\frac{\alpha+j}{n})\] so that \[\varphi_{\beta,\rho}(\tilde{\rho}_{n}(X))=-\frac{1}{m}\sum_{j=0}^{n-1}\rho \left(Y_{m}(\frac{\alpha+j}{n})-p^{m-1}Y_{m}(p\frac{\alpha+j}{n})\right).\] Then (126) follows from (116). Since \(p\) is prime to \(n\) and the rational numbers \(p\frac{\alpha+j}{n}\in{\mathbb{Q}}/{\mathbb{Z}}\) form the same subset as the set made by the \(\frac{p\alpha+j}{n}\), we derive \[\sum_{j=0}^{n-1}Y_{m}(\frac{\alpha+j}{n})=n^{m}Y_{m}(\alpha)\,,\ \ \sum_{j=0}^ {n-1}Y_{m}(p\frac{\alpha+j}{n})=n^{m}Y_{m}(p\alpha).\] ∎ ### The KMS\({}_{\beta}\) condition The main result of this section is the following **Theorem 7.11****.**: _For any \(\beta\in D_{p}\), \(\beta\neq 1\) and \(\rho:{\mathbb{Q}}^{\rm cyc,p}\hookrightarrow{\mathbb{C}}_{p}\), the linear form \(\varphi_{\beta,\rho}\) fulfills the KMS\({}_{\beta}\) condition:_ \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=\varphi_{\beta,\rho}(y\,x)\,,\quad~ {}\forall x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}.\] (127) _Moreover the partition function is the \(p\)-adic \(L\)-function_ \[Z(\beta):=\varphi_{\beta,\rho}(1)=L_{p}(\beta,1)\] (128) _which does not vanish for \(\beta\in D_{p}\)._ Proof.: We fix \(x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\), then after multiplication by \(\beta-1\), both sides of (127) are analytic functions of \(\beta\in D_{p}\). We first assume that \(\beta\neq 1\); we shall consider the case \(\beta=1\) separately later. Since any element of the algebra \({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\) can be written as a finite linear combination of \(\tilde{\mu}_{n}X\mu_{m}^{*}\), for \(X\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), we may assume that \[x=\tilde{\mu}_{n}X\mu_{m}^{*}\,,\ \ y=\tilde{\mu}_{s}Y\mu_{t}^{*}\] where \(n,m\in I(p)\), \((n,m)=1\), \(s,t\in I(p)\), \((s,t)=1\) and \(X,Y\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\). Then, we use the presentation of \({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\) to compute \(xy=\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}\,.\) Let \(u\) be the gcd of \(m=um^{\prime}\) and \(s=us^{\prime}\). One has \[\mu^{*}_{m}\,\tilde{\mu}_{s}=\mu^{*}_{m^{\prime}}\,\mu^{*}_{u}\,\tilde{\mu}_{u }\tilde{\mu}_{s^{\prime}}=u\mu^{*}_{m^{\prime}}\,\tilde{\mu}_{s^{\prime}}=u\, \tilde{\mu}_{s^{\prime}}\mu^{*}_{m^{\prime}}\] \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{n}\,X\,\tilde{\mu}_{s^{\prime}}\mu^{*}_{m^{\prime}}\,Y\,\mu^{*}_{t}=\,u\, \tilde{\mu}_{n}\,\tilde{\mu}_{s^{\prime}}\sigma_{s^{\prime}}(X)\sigma_{m^{ \prime}}(Y)\mu^{*}_{m^{\prime}}\,\mu^{*}_{t}\] Let \(v\) be the gcd of \(ns^{\prime}=vw\) and \(m^{\prime}t=vz\). One has \(\tilde{\mu}_{n}\,\tilde{\mu}_{s^{\prime}}=\tilde{\mu}_{w}\,\tilde{\mu}_{v}\), \(\mu^{*}_{m^{\prime}}\,\mu^{*}_{t}=\mu^{*}_{v}\,\mu^{*}_{z}\) \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{w}\,\tilde{\mu}_{v}\,\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(y)\,\mu^{*}_ {v}\,\mu^{*}_{z}=u\,\tilde{\mu}_{w}\,\tilde{\rho}_{v}(\sigma_{s^{\prime}}(X) \sigma_{m^{\prime}}(Y))\,\mu^{*}_{z}\,.\] We obtain \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{w}\,\tilde{\rho}_{v}(\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(Y))\,\mu^{*} _{z}\,,\ \ \frac{w}{z}=\frac{n}{m}\frac{s}{t}.\] (129) It follows that unless \(s=m\) and \(t=n\) one has \(\frac{w}{z}\neq 1\) and \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=\varphi_{\beta,\rho}(y\,x)=0.\] (130) Thus we can assume that \(s=m\) and \(t=n\). Then we have \[x\sigma^{(\beta)}(y)=m\left(\frac{n}{m}\right)^{(\beta)}\tilde{\mu}_{n}\,XY\, \mu^{*}_{n}=m\left(\frac{n}{m}\right)^{(\beta)}\tilde{\rho}_{n}(XY)\] so that, by (126) one derives \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=m\left(\frac{n}{m}\right)^{(\beta)} \langle n\rangle^{1-\beta}\varphi_{\beta,\rho}(XY).\] (131) Similarly one has, by applying again (126) \[yx=n\tilde{\mu}_{m}YX\mu_{m}^{*}\,,\ \ \varphi_{\beta,\rho}(y\,x)=n\langle m \rangle^{1-\beta}\varphi_{\beta,\rho}(XY).\] Thus (127) follows from the equality \[m\left(\frac{n}{m}\right)^{(\beta)}\langle n\rangle^{1-\beta}=n\langle m \rangle^{1-\beta}\] which in turn derives from (98) and (100). Now, we turn to the normalization factor (_i.e._ partition function) in (125) which is given by \[Z(\beta):=\varphi_{\beta,\rho}(1)=\frac{1}{q}\sum_{1\leq c<q\atop c\notin p{ \mathbb{N}}}\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty} \binom{1-\beta}{j}\left(\frac{q}{c}\right)^{j}B_{j}\,.\] (132) This is the \(p\)-adic \(L\)-function for the character \(\chi=1\) (_cf._[37], Chapter 5, Theorem 5.11) \[Z(\beta)=L_{p}(\beta,1).\] (133) Moreover, notice that the Iwasawa construction of \(L\)-functions (_cf._[37], Chapter 7, Theorem 7.10) yields a formal power series \(\frac{1}{2}g(T)\in{\mathbb{Z}}_{p}[[T]]^{\times}\) such that (with \(q\) as in (89)) the following equality holds \[L_{p}(\beta,1)=g\left((1+q)^{\beta}-1\right)/\left(1-(1+q)^{1-\beta}\right)\,, \quad~{}\forall\beta\in D_{p}.\] (134) Since \(\frac{1}{2}g(T)\in{\mathbb{Z}}_{p}[[T]]^{\times}\) is invertible (_cf._[37] Lemma 7.12), this gives the required result. ∎ Note that \(Z(\beta)\) has a pole at \(\beta=1\), with residue given by \[\frac{1}{q}\sum_{1\leq c<q\atop c\notin p{\mathbb{N}}}1=\frac{\varphi(q)}{q}= \frac{p-1}{p}\,.\] **Proposition 7.12****.**: _When \(\beta\to 1\) one has_ \[\lim_{\beta\to 1}Z(\beta)^{-1}Z_{\rho}(\frac{a}{b},\beta)=\left\{\begin{array} []{ll}1&\hbox{if}\ \frac{a}{b}\in{\mathbb{Z}}\\ 0&\hbox{otherwise.}\end{array}\right.\] (135) Proof.: Assume first that \(\frac{a}{b}\notin{\mathbb{Z}}\). Then \(\xi=\rho(\zeta_{a/b})\) is a non-trivial root of unity, whose order \(m>1\) divides \(b\) which is prime to \(p\) and hence prime to \(q\). Thus using the decomposition \({\mathbb{Z}}/bq{\mathbb{Z}}={\mathbb{Z}}/q{\mathbb{Z}}\times{\mathbb{Z}}/b{ \mathbb{Z}}\) we get \[\sum_{1\leq c<bq\atop c\notin p{\mathbb{N}}}\xi^{c}=\varphi(q)\sum_{n\in{ \mathbb{Z}}/b{\mathbb{Z}}}\xi^{n}=0.\] If \(\frac{a}{b}\in{\mathbb{Z}}\) the result follows from the above discussion.∎ Notice in particular that the limit of the functional values \(Z(\beta)^{-1}Z(\frac{a}{b},\beta)\) as \(\beta\to 1\) is independent of values of \(\rho\) (_i.e._ independent of the choice of \(\sigma\in X_{p}\)). In the complex case, the functional values for \(\beta>1\), are given by the formula (24). In that case, we shall now check directly that for \(\beta\in{\mathbb{C}}\), \(\Re(\beta)>1\), the functional values determine \(\rho:{{\mathbb{Q}}^{\rm cyc}}\to{\mathbb{C}}\) as an embedding of the abstract cyclotomic field \({{\mathbb{Q}}^{\rm cyc}}\) in \({\mathbb{C}}\). **Lemma 7.13****.**: \((1)\) _Let \(\lambda\in\hat{\mathbb{Z}}^{*}\), \(\lambda\neq\pm 1\). Then the graph of the multiplication by \(\lambda\) in \({\mathbb{Q}}/{\mathbb{Z}}\) is a dense subset of \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\)._ \((2)\) _Let \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\). Assume that \(\theta\notin\{\pm p^{\mathbb{Z}}\}\). Then the graph of \(\theta\) is dense in \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\)._ Proof.: \((1)\) The set \(G=\{(\alpha,\lambda\alpha)\mid\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\}\) is a subgroup of \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\) and so is its closure \(\bar{G}\). If \(G\) were not dense, then there would exist a non-trivial character \(\chi\) of the compact group \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\) whose kernel contains \(\bar{G}\). Thus there would exist a non-zero pair \((n,m)\in{\mathbb{Z}}^{2}\) such that \(n\alpha+m\lambda\alpha\in{\mathbb{Z}}\), for all \(\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\). This would imply that the multiplication by \(\lambda\in\hat{\mathbb{Z}}^{*}\) in the group \({\mathbb{Q}}/{\mathbb{Z}}={\mathbb{A}}_{{\mathbb{Q}},\,f}/\hat{\mathbb{Z}}\) (\({\mathbb{A}}_{{\mathbb{Q}},\,f}\) are the finite adèles) ought to fulfill \(n\alpha+m\lambda\alpha\in\hat{\mathbb{Z}}\,,\quad~{}\forall\alpha\in{\mathbb{A }}_{{\mathbb{Q}},\,f}\). This implies \((n+m\lambda_{p})\alpha\in{\mathbb{Z}}_{p}\,,\quad~{}\forall\alpha\in{\mathbb{Q }}_{p}\) and hence \(n+m\lambda_{p}=0\) for all primes \(p\). If \(n/m\notin\{\pm 1\}\), this contradicts the fact that \(\lambda\in\hat{\mathbb{Z}}^{*}\)_i.e._\(\lambda_{p}\in\hat{\mathbb{Z}}_{p}^{*}\) for all \(p\). \((2)\) By Lemma 8.6 the group \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) is the group of automorphisms of the group \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) viewed as the additive group \(\Gamma=\prod^{res}_{\ell\neq p}{\mathbb{Q}}_{\ell}/{\mathbb{Z}}_{\ell}\). Let \(\lambda\in G_{p}\) represent \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\). Then the same proof as in \((1)\) shows that if the graph of \(\theta\) is not dense, there exists a non-zero pair \((n,m)\in{\mathbb{Z}}^{2}\) such that \(n+m\lambda_{\ell}=0\) for all primes \(\ell\neq p\). It follows that \(-n/m\in\{\pm p^{\mathbb{Z}}\}\) and \(\theta\in\{\pm p^{\mathbb{Z}}\}\).∎ From Lemma 7.13 we derive that, if \(f:\{z\in{\mathbb{C}}\mid|z|=1\}\to{\mathbb{C}}\) is a continuous non-constant function, and \(\rho_{j}:{{\mathbb{Q}}^{\rm cyc}}\to{\mathbb{C}}\), are injective, an equality of the form \[f(\rho_{1}(\zeta_{a/b}))=f(\rho_{2}(\zeta_{a/b}))\,,\quad~{}\forall a/b\in{ \mathbb{Q}}/{\mathbb{Z}}\] (136) necessarily implies that \(\rho_{2}=\rho_{1}\) or \(\rho_{2}=\bar{\rho}_{1}\). In the latter case one also gets \[f(\bar{z})=f(z)\,,\quad~{}\forall z,\ |z|=1.\] By uniqueness of the Fourier decomposition however, this case cannot occur if \(f(z)=\sum_{n=1}^{\infty}n^{-\beta}z^{n}\), for \(\Re\mathfrak{e}(\beta)>1\). Next, we fix an integer \(\beta=1-m=1-k\varphi(q)\), \(k>0\), and we investigate the dependence on \(\rho\) in the expressions (121). For a chosen pair of embeddings \(\rho,\rho^{\prime}\), assume that \(Z_{\rho}(\frac{a}{b},\beta)=Z_{\rho^{\prime}}(\frac{a}{b},\beta)\) holds for all \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), _i.e._ the equality holds for all fractions with denominator \(b\) prime to \(p\). It follows from (121) that one has (with \({\rm Fr}\) the Frobenius automorphism of \(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}\)) \[(1-p^{m-1}{\rm Fr})^{-1}Z_{\rho}(\frac{a}{b},\beta)=-\frac{b^{m-1}}{m}\sum_{1 \leq c\leq b}\rho(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})\in\widehat{{\mathbb{Q}} _{p}^{\rm ur}}.\] (137) Thus we get \[\sum_{1\leq c\leq b}\rho(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})=\sum_{1\leq c \leq b}\rho^{\prime}(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})\qquad\forall a/b\in{ ({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (138) Since both \(\rho\) and \(\rho^{\prime}\) are isomorphisms of the group of roots of unity in \({\mathbb{Q}}^{\rm cyc,p}\) with the group of roots of unity in \({\mathbb{C}}_{p}\) of order prime to \(p\), there exists an automorphism \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\) such that \(\rho^{\prime}(\zeta_{a/b})=\rho(\zeta_{\theta(a/b)})\) for all \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). One has \[\sum_{1\leq c\leq b}\rho^{\prime}(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})=\sum_{1 \leq c\leq b}\rho(\zeta_{\theta(c/b)}^{a})\,B_{m}(\frac{c}{b})=\sum_{1\leq c \leq b}\rho(\zeta_{a/b}^{c})\,B_{m}(\theta^{-1}(\frac{c}{b})).\] By uniqueness of the Fourier transform for the finite group \({\mathbb{Z}}/b{\mathbb{Z}}\), (138) yields the equality \[B_{m}(\theta^{-1}(\frac{c}{b}))=B_{m}(\frac{c}{b})\qquad\forall c/b\in{({ \mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (139) **Lemma 7.14****.**: _Let \(p>2\) and let \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\). If \(\theta\in\{\pm 1\}\) one has_ \[Z_{\rho}(\frac{a}{b},\beta)=Z_{\theta\circ\rho}(\frac{a}{b},\beta)\,,\quad~{} \forall a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}},\ \beta\in D_{p}.\] (140) _If \(\theta\notin\{\pm 1\}\) and \(\beta=1-m=1-k\varphi(q)\), \(k>0\), then the functionals \(Z_{\rho}(\cdot,\beta)\) and \(Z_{\theta\circ\rho}(\cdot,\beta)\) are distinct._ Proof.: To prove (140) we can assume that \(\theta=-1\)_i.e._ that \(\theta(\zeta_{a/b})=\zeta_{a/b}^{-1}\) for all \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Then we have, with \(\rho^{\prime}=\theta\circ\rho\): \(\rho^{\prime}(\zeta_{a/b}^{c})=\rho(\zeta_{a/b}^{b-c})\). Let first \(\beta=1-m=1-k\varphi(q)\). One has \[\sum_{1\leq c\leq b}\rho^{\prime}(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})=\sum_{0 \leq c\leq b-1}\rho(\zeta_{a/b}^{c})\,B_{m}(\frac{b-c}{b})\,.\] Since \(m=k\varphi(q)\) is even, the Bernoulli polynomial \(B_{m}\) fulfills the equality \[B_{m}(1-x)=B_{m}(x)\,,\quad~{}\forall m\in 2{\mathbb{N}}\,.\] (141) Thus (140) follows for all values \(\beta=1-m=1-k\varphi(q)\). Since these values admit \(0\) as an accumulation point, one derives the equality of the analytic functions on their domain \(D_{p}\). Now, we assume that \(\theta\notin\{\pm p^{\mathbb{Z}}\}\). Then it follows from Lemma 7.13 that the graph of \(\theta\) is dense in \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\). Thus (139) implies that \(B_{m}(x)\) is constant which is a contradiction. It remains to show that for non-zero powers \(p^{a}\) of \(p\) one cannot have an equality of the form \[B_{m}(x)=B_{m}(p^{a}x-[p^{a}x])\,,\quad~{}\forall x\in[0,1]\] where \([p^{a}x]\) is the integral part of \(p^{a}x\). In fact, this would imply that \(B_{m}(x)-B_{m}(p^{a}x)\) has infinitely many zeros, thus \(B_{m}(x)=B_{m}(p^{a}x)\) which is a contradiction. ∎ ### Extension of the KMS\({}_{\beta}\) theory to the covering of \({\mathbb{C}}_{p}\) In this section we show that the construction of the KMS\({}_{\beta}\) states \(\varphi_{\beta,\rho}\), for \(\beta\in D_{p}\), extends naturally to the covering of \({\mathbb{C}}_{p}\) defined by the following group homomorphism \[M=D(1,1^{-})\ni\lambda\mapsto\beta=\ell(\lambda)=\frac{\log_{p}\lambda}{\log_{ p}(1+q)}\in{\mathbb{C}}_{p}\] (142) where \(M=D(1,1^{-})\) is the open unit disk in \({\mathbb{C}}_{p}\) with radius \(1\), viewed as a multiplicative group. Up to the normalization factor \(\log_{p}(1+q)\), this group homomorphism coincides with the definition of the Iwasawa logarithm, it is surjective with kernel the subgroup of roots of unity of order a \(p\)-power (_cf._[32], Theorem p. 257) and it defines by restriction a bijection \[\ell:\{\lambda\in M\mid|\lambda-1|_{p}<p^{-1/(p-1)}\}\stackrel{{ \sim}}{{\to}}D_{p}\] (143) whose inverse is given by the map \[D_{p}\ni\beta\mapsto\psi(\beta)=(1+q)^{\beta}={\rm exp}(\beta\log_{p}(1+q)).\] (144) By construction, this local section is a group homomorphism which allows one to view the additive group \(D_{p}\) as a subgroup of \(M\). We start by extending the definition of the functions \(r^{(\beta)}\) as in (98) which were implemented in the construction of the automorphisms \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) (_cf._ Proposition 7.3). For \(r\in{\mathbb{Z}}_{(p)}^{\times}\) the equality \[i_{p}(r)=\frac{\log_{p}(r)}{\log_{p}(1+q)}\in{\mathbb{Z}}_{p}\] (145) defines a group homomorphism from \({\mathbb{Z}}_{(p)}^{\times}\) to the additive group \({\mathbb{Z}}_{p}\). **Lemma 7.15****.**: _For \(\beta\in D_{p}\), \(r\in{\mathbb{Z}}_{(p)}^{\times}\) and \(\lambda=(1+q)^{\beta}\) one has_ \[\langle r\rangle^{\beta}=\lambda^{i_{p}(r)}\,,\ \ r^{(\beta)}=\omega(r)\, \lambda^{i_{p}(r)}.\] (146) Proof.: One has \(\log_{p}(r)=i_{p}(r)\log_{p}(1+q)\in q{\mathbb{Z}}_{p}\). Thus \(|\beta\log_{p}(r)|_{p}<p^{-1/(p-1)}\) and \[\langle r\rangle^{\beta}={\rm exp}(\beta\log_{p}(r))={\rm exp}(\beta i_{p}(r) \log_{p}(1+q))=(1+q)^{\beta i_{p}(r)}=\lambda^{i_{p}(r)}.\] The second equality follows from the definition (98).∎ Proposition 7.3 and its proof thus extend from \(D_{p}\) to \(M\). This means that for \(\lambda\in M\) there exists a unique automorphism \(\sigma[\lambda]\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) such that \[\sigma[\lambda](\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*})=\omega(b/a)\lambda^{i_{p} (b/a)}\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*}\,,\quad~{}\forall a,b\in I(p),\ \gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (147) Next, we extend the construction of the linear forms \(\varphi_{\beta,\rho}\) given in §7.3. It is sufficient to extend the definition of the functions of Lemma 7.6 (which we proved to be independent of the choice of \(f\neq 0\) multiple of \(bq\)) \[Z_{\rho}(\frac{a}{b},\beta):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{\mathbb {N}}}\rho(\zeta_{a/b}^{c})\,\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j= 0}^{\infty}\binom{1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j},\qquad\beta\in D _{p}.\] (148) To define the sought for extension it is convenient to express the above function in terms of the \(p\)-adic \(L\)-functions \(L_{p}(\beta,\chi)\) associated to even Dirichlet characters of conductor \(f_{\chi}\) prime to \(p\). By definition, a Dirichlet character \(\chi\) is a character of the multiplicative group \(\hat{\mathbb{Z}}^{*}\) and its conductor \(f_{\chi}\) is the integer such that the kernel of \(\chi\) is the kernel of the projection \(\hat{\mathbb{Z}}^{*}\to({\mathbb{Z}}/f_{\chi}{\mathbb{Z}})^{*}\). The definition of \(L_{p}(\beta,\chi)\) is similar to (148) precisely as follows \[L_{p}(\beta,\chi):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}\chi( c)\,\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1- \beta}{j}\left(\frac{f}{c}\right)^{j}B_{j}\] (149) where \(f\) is any multiple of \(pf_{\chi}\) and where \(\chi\) has been extended to a periodic function of period \(f_{\chi}\) vanishing outside \(({\mathbb{Z}}/f_{\chi}{\mathbb{Z}})^{*}\). We recall that the \(L\)-function \(L_{p}(\beta,\chi)\) is identically zero when the character \(\chi\) is odd, _i.e._ when \(\chi(-1)=-1\) (_cf._[37] Remarks p. 57). Moreover when \(\chi\) is even, non-trivial, and its conductor is prime to \(p\), there exists an analytic function \(H_{\chi}\) on \(M\) such that (_cf._[37] Theorem 7.10) \[L_{p}(\beta,\chi)=H_{\chi}((1+q)^{\beta})\,,\quad~{}\forall\beta\in D_{p}\,.\] (150) The extension of the functions \(Z_{\rho}(\frac{a}{b},\beta)\) to \(M\) is a consequence of the following **Lemma 7.16****.**: _For any \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) there exists coefficients \(c(d,\chi)\in{\mathbb{C}}_{p}\) such that_ \[Z_{\rho}(\frac{a}{b},\beta)=\sum_{d|b,\,\chi}c(d,\chi)L_{p}(\beta,\chi)d^{-1} \langle d\rangle^{1-\beta}\prod(1-\chi(\ell)\ell^{-1}\langle\ell\rangle^{1- \beta})\] (151) _where \(d\) varies among the divisors of \(b\), and, for fixed \(d\), \(\chi\) varies among the set of Dirichlet characters whose conductor \(f_{\chi}\) divides \(m=b/d\). The integers \(\ell\) are the primes which divide \(m/f_{\chi}\) but not \(f_{\chi}\)._ Proof.: Let \(b\) be an integer prime to \(p\), and \(g\in C({\mathbb{Z}}/b{\mathbb{Z}},{\mathbb{C}}_{p})\). The expression \[Y(g,\beta):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}g(c)\,\frac{ \langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1-\beta}{j}\left (\frac{f}{c}\right)^{j}B_{j},\qquad\beta\in D_{p}\] (152) is independent of the choice of the multiple \(f\neq 0\) of \(bq\). Let \(\chi\) be a Dirichlet character (with values in \({\mathbb{C}}_{p}\)) with conductor \(f_{\chi}\) and let \(m\) be a multiple of \(f_{\chi}\). Then the following defines a multiplicative map from \({\mathbb{Z}}/m{\mathbb{Z}}\) to \({\mathbb{C}}_{p}\) \[z(\chi,m)(c)=\left\{\begin{array}[]{ll}\chi(c)&\hbox{if}\,c\in({\mathbb{Z}}/m{ \mathbb{Z}})^{*}\\ 0&\hbox{otherwise.}\end{array}\right.\] (153) If \(m\) divides \(b\) and one replaces \(\chi\) with \(z(\chi,m)\) in (149) one obtains instead of \(L_{p}(\beta,\chi)\) the function \[Y(z(\chi,m),\beta)=L_{p}(\beta,\chi)\prod(1-\chi(\ell)\ell^{-1}\langle\ell \rangle^{1-\beta})\] (154) where the integers \(\ell\) are the primes which divide \(m/f_{\chi}\) without dividing \(f_{\chi}\). Next, define for any divisor \(d\) of \(b\) and any function \(h\in C({\mathbb{Z}}/m{\mathbb{Z}},{\mathbb{C}}_{p})\), \(m=b/d\), \[e_{d}(h)(a)=\left\{\begin{array}[]{ll}h(a/d)&\hbox{if}\,d|a\\ 0&\hbox{otherwise.}\end{array}\right.\] One then gets \[Y(e_{d}(h),\beta)=d^{-1}\langle d\rangle^{1-\beta}Y(h,\beta).\] (155) Thus using (154) and (155) it is enough to prove that for any function \(g\in C({\mathbb{Z}}/b{\mathbb{Z}},{\mathbb{C}}_{p})\) there exists coefficients \(c(d,\chi)\in{\mathbb{C}}_{p}\) such that \[g(c)=\sum_{d|b,\,\chi}c(d,\chi)e_{d}(z(\chi,b/d)).\] It is in fact enough to check this for \(g=\delta_{a}\) where \(a\in{\mathbb{Z}}/b{\mathbb{Z}}\). Let then \(d\) be the gcd of \(a\) and \(b\). One has \(\delta_{a}=e_{d}(\delta_{c})\) where \(c=a/d\) is prime to \(m=b/d\). Moreover for any element \(c\in({\mathbb{Z}}/m{\mathbb{Z}})^{*}\) one has \[\delta_{c}(x)=\frac{1}{\varphi(m)}\sum_{\chi,\,f_{\chi}|m}\chi(c)^{-1}z(\chi,m )(x)\,,\quad~{}\forall x\in{\mathbb{Z}}/m{\mathbb{Z}},\] which gives the required equality.∎ We thus obtain the following extension of Theorem 7.11 **Theorem 7.17****.**: _There exists an analytic family of functionals \(\psi_{\lambda,\rho}\), \(\lambda\in M\), on \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) such that_ \(\bullet\)_\(\psi_{\lambda,\rho}(1)=1.\)_ \(\bullet\)_\(\psi_{\lambda,\rho}\) fulfills the KMS condition_ \[\psi_{\lambda,\rho}(x\sigma[\lambda](y))=\psi_{\lambda,\rho}(y\,x)\,,\quad~{} \forall x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}.\] (156) \(\bullet\) _For \(\beta\in D_{p}\) and \(\lambda=(1+q)^{\beta}\) one has_ \[\psi_{\lambda,\rho}=Z(\beta)^{-1}\varphi_{\beta,\rho}\,.\] Proof.: It follows from (134) that there exists an analytic function \(z(\lambda)\) of \(\lambda\in M\) such that \[Z(\beta)^{-1}=(1+q-\lambda)z(\lambda)\,,\ \ \lambda=(1+q)^{\beta}.\] By applying (150), Lemma 7.15 and Lemma 7.16, we see that there exists, for \(b\in I(p)\) and \(a/b\notin{\mathbb{Z}}\), an analytic function \(H_{a,b}(\lambda)\) of \(\lambda\in M\) such that \[Z_{\rho}(\frac{a}{b},\beta)=H_{a,b}(\lambda)\,,\ \ \lambda=(1+q)^{\beta}.\] This proves the existence of the analytic family of functionals \(\psi_{\lambda,\rho}\) fulfilling the required conditions. ∎ ## 8. Extension of the \(p\)-adic valuation to \({{\mathbb{Q}}^{\rm cyc}}\) For a global field \({\mathbb{K}}\) of positive characteristic (_i.e._ a function field associated to a projective, non-singular curve \(C\) over a finite field \({\mathbb{F}}_{q}\)) it is a well known fact that the space of valuations of the maximal abelian extension \({\mathbb{K}}^{\rm ab}\) of \({\mathbb{K}}\) has a geometric meaning. In fact, for each finite extension \(E\) of \(\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}}\subset{\mathbb{K}}^ {\rm ab}\) the space \({\rm Val}(E)\) of (discrete) valuations of \(E\) is turned into an algebraic, one-dimensional scheme whose non-empty open sets are the complements of finite subsets \(F\subset{\rm Val}(E)\). The structure sheaf is locally defined by the intersection \(\bigcap_{F}R\) of the valuation rings inside \(E\). Then the space \({\rm Val}({\mathbb{K}}^{\rm ab})\) is the projective limit of the schemes \({\rm Val}(E)\), \(E\subset{\mathbb{K}}^{\rm ab}\). For the global field \({\mathbb{K}}={\mathbb{Q}}\) of rational numbers, one can consider its maximal abelian extension \({{\mathbb{Q}}^{\rm cyc}}\) as an abstract field (_cf._ Definition 8.1) and try to follow a similar idea. In Section 9, we will see however that the space \({\rm Val}({{\mathbb{Q}}^{\rm cyc}})\) provides only a rough analogue, in characteristic zero, of \({\rm Val}({\mathbb{K}}^{\rm ab})\). This section develops the preliminary step of presenting 5 different but equivalent descriptions of the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) of extensions of the \(p\)-adic valuation of \({\mathbb{Q}}\) to the abstract cyclotomic field \({{\mathbb{Q}}^{\rm cyc}}\). The field \({{\mathbb{Q}}^{\rm cyc}}\) is the composite of the field generated by roots of unity of order a \(p\)-power and the field \({\mathbb{Q}}^{\rm cyc,p}\) generated by the roots of unity of order prime to \(p\). We describe canonical isomorphisms of \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) with¹: [FOOTNOTE:1][ENDFOOTNOTE] \((1)\) The space of sequences of irreducible polynomials \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), fulfilling the basic conditions of the Conway polynomials (_cf._ Theorem 8.7). \((2)\) The space \(\Sigma_{p}\) of bijections of the monoid \({{\mathcal{M}}{(p)}}=\mu^{(p)}\cup\{0\}\) of roots of unity of order prime to \(p\) which commute with their conjugates, as in Definition 8.5 (_cf._ Proposition 8.8). \((3)\) The space \({\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) of field homomorphisms, where \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) is the fixed field under the Frobenius automorphism (_cf._ Proposition 8.12). \((4)\) The quotient of the space \(X_{p}\) of Definition 4.3 by the action of \({\rm Gal}(\bar{\mathbb{F}}_{p})\) (_cf._ Proposition 8.14). \((5)\) The algebraic spectrum of the quotient algebra \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]/J_{p}\), where \(J_{p}\) is the reduction modulo \(p\) of the cyclotomic ideal (_cf._ Definition 8.1 and Proposition 8.16). Incidentally, we notice that \((1)\) describes the link between \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and the explicit construction of an algebraic closure \(\bar{\mathbb{F}}_{p}\) of \({\mathbb{F}}_{p}\), by means of a sequence of irreducible polynomials over \({\mathbb{F}}_{p}\), fulfilling the basic conditions of the Conway polynomials². Theorem 8.7 states that the map which associates to a valuation \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) the sequence \(\{P_{n}\}\) of characteristic polynomials for the action (by multiplication) of the primitive root \(\xi_{\frac{1}{p^{n}-1}}\in{\mathbb{Q}}^{\rm cyc,p}\) on the residue field of the restriction of \(v\) to \({\mathbb{Q}}^{\rm cyc,p}\), determines a bijection between \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and sequences of polynomials in \({\mathbb{F}}_{p}[T]\) fulfilling the basic conditions of the Conway polynomials. [FOOTNOTE:2][ENDFOOTNOTE] **Definition 8.1****.**: _The abstract cyclotomic field \({{\mathbb{Q}}^{\rm cyc}}\) is the quotient of the group ring \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) by the ideal \(J\) generated by the idempotents_ \[\pi_{n}=\frac{1}{n}\sum_{j=0}^{n-1}e(\frac{j}{n}),\qquad n\geq 2.\] (157) In general, if we let \[\sigma_{k}(x)=\sum_{j=0}^{k-1}\,x^{j},\] (158) then one knows that the \(n\)-th cyclotomic polynomial \(\Phi_{n}(x)\) is the gcd of the polynomials \(\sigma_{m}(x^{d})\), for \(m>1\), \(m|n\) and \(d=n/m\). For \(x=e(1/n)\), and \(n=md\) one has \[\sigma_{m}(x^{d})=\sum_{j=0}^{m-1}\,e(j/m)=m\,\pi_{m}\in J\] thus \(\Phi_{n}(e(1/n))\in J\). It follows that the homomorphism \[\rho_{0}:{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]/J\to{\mathbb{C}}\,,\ \ \rho_{ 0}(e(\gamma))=e^{2\pi i\gamma}\] (159) induces an isomorphism of \({{\mathbb{Q}}^{\rm cyc}}\) with the subfield of \({\mathbb{C}}\) generated by roots of unity. Using the identification \({\mathbb{Q}}/{\mathbb{Z}}={\mathbb{A}}_{{\mathbb{Q}}}^{f}/\hat{\mathbb{Z}}\) the group \(\hat{\mathbb{Z}}^{*}\) acts by automorphisms of \({\mathbb{Q}}/{\mathbb{Z}}\) and hence by automorphisms of the group ring \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\). This action preserves globally the \(n\)-torsion in \({\mathbb{Q}}/{\mathbb{Z}}\) and hence fixes each of the projection \(\pi_{n}\). It follows that it leaves the ideal \(J\) globally invariant and hence it induces an action on the quotient field \({{\mathbb{Q}}^{\rm cyc}}\). This action gives the Galois group \(G={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\simeq\hat{\mathbb{Z}}^{*}\) which acts on roots of unity as it acts on \({\mathbb{Q}}/{\mathbb{Z}}\). For each prime \(p\), one has (\(\ell=\) rational prime) \[G=\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}={\mathbb{Z}}_{p}^{*}\times\prod_{\ell \neq p}{\mathbb{Z}}_{\ell}^{*}={\mathbb{Z}}_{p}^{*}\times G_{p}.\] (160) One lifts \({\mathbb{Z}}_{p}^{*}\) to the subgroup \({\mathbb{Z}}_{p}^{*}\times 1\subset G\), with all components equal to \(1\) except at \(p\). This subgroup acts trivially on \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Its fixed subfield \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) is the subfield of \({{\mathbb{Q}}^{\rm cyc}}\) generated over \({\mathbb{Q}}\) by the group \(\mu^{(p)}\subset{{\mathbb{Q}}^{\rm cyc}}\) of roots of unity of order prime to \(p\). It coincides with the _inertia subfield_ \[{{\mathbb{Q}}^{\rm cyc}}\cap{\mathbb{Q}}_{p}^{\rm ur}\subset{{\mathbb{Q}}^{\rm cyc}}\] (161) for any extension \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) of the \(p\)-adic valuation to \({{\mathbb{Q}}^{\rm cyc}}\). More precisely let \(({{\mathbb{Q}}^{\rm cyc}})_{v}\) be the completion of \({{\mathbb{Q}}^{\rm cyc}}\) for the valuation \(v\). Then one knows that the composite subfield \({\mathbb{Q}}_{p}\cdot{{\mathbb{Q}}^{\rm cyc}}\subset({{\mathbb{Q}}^{\rm cyc}}) _{v}\) is the maximal abelian extension \({\mathbb{Q}}_{p}^{\rm ab}\) of \({\mathbb{Q}}_{p}\). This extension is the composite (_cf._[34]) \[{\mathbb{Q}}_{p}^{\rm ab}={\mathbb{Q}}_{p}^{\rm ur}\cdot{\mathbb{Q}}_{p^{ \infty}}\] (162) where \({\mathbb{Q}}_{p}^{\rm ur}\) denotes the maximal unramified extension of \({\mathbb{Q}}_{p}\) and \({\mathbb{Q}}_{p^{\infty}}\) is obtained by adjoining to \({\mathbb{Q}}_{p}\) all roots of unity of order a \(p\)-power. The translation Theorem of Galois theory gives a canonical isomorphism (by restriction) of Galois groups \[{\rm Gal}({\mathbb{Q}}_{p}^{\rm ab}:{\mathbb{Q}}_{p})\stackrel{{ \sim}}{{\to}}{\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{{\mathbb{Q}}^{\rm cyc}}\cap{ \mathbb{Q}}_{p}),\qquad\alpha\mapsto\alpha|_{{\mathbb{Q}}^{\rm cyc}}.\] (163) The _decomposition subfield_: \({{\mathbb{Q}}^{\rm cyc}}\cap{\mathbb{Q}}_{p}\) is independent of the choice of the valuation \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) since \(G\) is abelian and acts transitively on \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\), more precisely one has the following classical result **Proposition 8.2****.**: \((1)\) _The group \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) is the group of automorphisms of the group \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\)._ \((2)\) _The inertia subfield \({\mathbb{Q}}^{\rm cyc,p}\) is the fixed subfield of \({\mathbb{Z}}_{p}^{*}\subset G\) and its Galois group is canonically isomorphic to \(G_{p}\) acting on \(\mu^{(p)}\subset{\mathbb{Q}}^{\rm cyc,p}\) as it acts on \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\)._ \((3)\) _Let \(f_{p}\in G_{p}\) be the element of \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) with all components equal to \(p\). Then the associated automorphism \({\rm Fr}\in{\rm Aut}({\mathbb{Q}}^{\rm cyc,p})\) is the unique automorphism which acts by \(x\mapsto x^{p}\) on the multiplicative group \(\mu^{(p)}\subset{\mathbb{Q}}^{\rm cyc,p}\)._ \((4)\) _The fixed subfield \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) of \({\rm Fr}\) is the decomposition subfield \({{\mathbb{Q}}^{\rm cyc}}\cap{\mathbb{Q}}_{p}\)._ \((5)\) _The group \(G={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\) acts transitively on \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) with isotropy \({\mathbb{Z}}_{p}^{*}\times f_{p}^{\hat{\mathbb{Z}}}\), where \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\) is the closure of \(f_{p}^{\mathbb{Z}}\)._ Proof.: \((1)\) Let \(\Gamma={({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) viewed as a discrete group. The Pontrjagin dual \(\hat{\Gamma}\) is the product \(\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}\). We claim that the group of automorphisms of \(\Gamma\) is \[{\rm Aut}(\Gamma)=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\,.\] (164) Indeed, one has \(\Gamma=\prod^{res}_{\ell\neq p}{\mathbb{Q}}_{\ell}/{\mathbb{Z}}_{\ell}\), so that the dual of \(\Gamma\) is \(\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}\). This is a compact ring which contains \({\mathbb{Z}}\) as a dense subring. Thus an automorphism \(\theta\) of the additive group is characterized by the assignment \(a=\theta(1)\) and is given by multiplication by \(a\). Invertibility shows that \(a\in\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\). This proves (164). \((2)\) Under the isomorphism (163) the Galois group \({\rm Gal}({\mathbb{Q}}_{p^{\infty}}:{\mathbb{Q}}_{p})\simeq{\mathbb{Z}}_{p}^{*}\) becomes the subgroup \({\mathbb{Z}}_{p}^{*}\times 1\subset G\). The fixed subfield of this subgroup is \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) and is the inertia subfield of \({{\mathbb{Q}}^{\rm cyc}}\). The quotient \(G/{\mathbb{Z}}_{p}^{*}\) is canonically isomorphic to \(G_{p}\). \((3)\) Under the isomorphism \({\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q}})=G_{p}\) the action of \({\rm Fr}\) on \(\mu^{(p)}\) corresponds to the multiplication by \(p\) in \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). \((4)\) The Galois group \({\rm Gal}({\mathbb{Q}}_{p}^{\rm ur}:{\mathbb{Q}}_{p})\simeq\hat{\mathbb{Z}}\) is topologically generated by the Frobenius automorphism \({\rm Fr}_{p}\) whose action on the roots of unity of order prime to \(p\) is given by \({\rm Fr}_{p}(\xi)=\xi^{p}\). Under the isomorphism (163) this automorphism restricts to the automorphism \({\rm Fr}\in{\rm Aut}({\mathbb{Q}}^{\rm cyc,p})\). Notice that the fields \({\mathbb{Q}}^{\rm cyc,p}\) and \({\mathbb{Q}}_{p}\) are linearly disjoint over their intersection \[K={\mathbb{Q}}^{\rm cyc,p}\cap{\mathbb{Q}}_{p}={{\mathbb{Q}}^{\rm cyc}}\cap{ \mathbb{Q}}_{p}\,.\] (165) Then, the translation theorem in Galois theory shows that, by restriction to \({\mathbb{Q}}^{\rm cyc,p}\), one has an isomorphism \[{\rm Gal}({\mathbb{Q}}_{p}^{\rm ur}:{\mathbb{Q}}_{p})\stackrel{{ \sim}}{{\to}}{\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:K),\qquad{\rm Fr}_{p}\mapsto{ \rm Fr}.\] This shows that \(K\) is the fixed subfield \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) of \({\rm Fr}\). \((5)\) It is well known that the Galois group acts transitively on extensions of a valuation. Moreover the isotropy subgroup is the subgroup of the Galois group corresponding to the decomposition subfield and is hence given by \({\mathbb{Z}}_{p}^{*}\times f_{p}^{\hat{\mathbb{Z}}}\). ∎ **Corollary 8.3****.**: _The natural map \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\to{\rm Val}_{p}({\mathbb{Q}}^{\rm cyc, p})\) given by restriction of valuations is equivariant and bijective._ Proof.: The restriction map is equivariant for the action of \(G\) on both spaces, these actions are transitive and have the same isotropy group so the restriction map is bijective.∎ In fact it is worth giving explicitly the unique extension of a valuation \(v\in{\rm Val}_{p}({\mathbb{Q}}^{\rm cyc,p})\) to \({{\mathbb{Q}}^{\rm cyc}}\). The latter field is obtained by adjoining to \({\mathbb{Q}}^{\rm cyc,p}\) primitive roots of unity of order a power of \(p\), _i.e._ a solution \(z\) of an equation of the form \[z^{(p-1)p^{m-1}}+z^{(p-2)p^{m-1}}+\ldots+1=0.\] One writes \(z=1+\pi\) and finds that the equation fulfilled by \(\pi\) is of Eisenstein type, the constant term being equal to \(p\), and reduces to \(\pi^{\varphi(n)}=0\), modulo \(p\). This shows that \[v(\pi)=\frac{v(p)}{\varphi(n)}\,,\ \ \varphi(n)=(p-1)p^{m-1}.\] Then the valuation \(v\), normalized so that \(v(p)=1\), extends uniquely to elements of the extension \({\mathbb{Q}}^{\rm cyc,p}[z]\) by setting \[v(a_{0}+a_{1}\pi+\ldots+a_{\varphi(n)-1}\pi^{\varphi(n)-1})=\inf\{v(a_{j})+ \frac{j}{\varphi(n)}\}.\] (166) **Remark 8.4****.**: The decomposition subfield \({\mathbb{Q}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\) is an infinite extension of \({\mathbb{Q}}\) which contains for instance \(\sqrt{n}\) for \(n\) a quadratic residue modulo \(p\). Its Galois group \({\rm Gal}({\mathbb{Q}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\) is the quotient of \(G_{p}\) by the closure of the group of powers of \(f_{p}\) and is a compact group which contains for each prime \(\ell\neq p\) the cyclic group of order \(\ell-1\) coming from the torsion part of \({\mathbb{Z}}_{\ell}^{*}\). **Definition 8.5****.**: _Let \({{\mathcal{M}}{(p)}}=\{0\}\cup\mu^{(p)}\) be the monoid obtained by adjoining a zero element to the multiplicative group \(\mu^{(p)}\). We denote by \(\Sigma_{p}\) the set of bijections \(s:{{\mathcal{M}}{(p)}}\to{{\mathcal{M}}{(p)}}\) which commute with all their conjugates \(R\circ s\circ R^{-1}\) under rotations \(R\) by elements of \(\mu^{(p)}\), and fulfill the relations: \(s(0)=1\), \(s^{p}=s\circ s\circ\ldots\circ s=id\)._ The maps \(s\) encode the addition of \(1\) on \({{\mathcal{M}}{(p)}}\), when one enriches the multiplicative structure of the monoid \({{\mathcal{M}}{(p)}}\) with an additive structure turning it to a field of characteristic \(p\) (_i.e._ an algebraic closure of \({\mathbb{F}}_{p}\)). Notice that using distributivity the addition of \(1\) encodes the full additive structure (_cf._[12]). **Lemma 8.6****.**: _The group \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) acts transitively on \(\Sigma_{p}\) with isotropy \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\)._ Proof.: We check that \(G_{p}\) acts transitively on \(\Sigma_{p}\). Let \(s_{j}\in\Sigma_{p}\), for \(j=1,2\) and let \({\mathbb{K}}(s_{j})\) be the two corresponding field structures on \({{\mathcal{M}}{(p)}}\). Then the two fields \({\mathbb{K}}(s_{j})\) are algebraic closures of \({\mathbb{F}}_{p}\) and hence they are isomorphic. We let \(\theta:{\mathbb{K}}(s_{1})\to{\mathbb{K}}(s_{2})\) be such an isomorphism. By construction \(\theta\) is an automorphism of the multiplicative group \(\mu^{(p)}\) and it transports the operation \(s_{1}\) of addition of \(1\) in \({\mathbb{K}}(s_{1})\) into the operation \(s_{2}\) of addition of \(1\) in \({\mathbb{K}}(s_{2})\). Since the Galois group of \(\bar{\mathbb{F}}_{p}\) is topologically generated by the Frobenius \(x\mapsto x^{p}\) one gets, using Galois theory, that the isotropy of any \(s\in\Sigma_{p}\) is the closure of the group of powers of \(f_{p}\), _i.e._ the subgroup \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\).∎ We are now ready to state the main result of this section **Theorem 8.7****.**: _An element \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) is entirely characterized by a sequence of polynomials \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\) of degree \(n\geq 1\), such that_ \(\bullet\) _each \(P_{n}(T)\) is monic and irreducible._ \(\bullet\)_\(T\in{\mathbb{F}}_{p}[T]/(P_{n}(T))\) is a generator of the multiplicative group of the quotient field._ \(\bullet\) _For any integer \(m|n\) and for \(d=(p^{n}-1)/(p^{m}-1)\), \(P_{m}(T^{d})\) is a multiple of \(P_{n}(T)\)._ Proof.: The first step in the proof is to construct a natural map \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\ni v\mapsto s_{v}\in\Sigma_{p}\). We know that \({\mathbb{Q}}_{p}\subset({{\mathbb{Q}}^{\rm cyc}})_{v}\) and that \(\mu^{(p)}\cup\{0\}\subset{{\mathbb{Q}}^{\rm cyc}}\), thus we consider the valuation ring \({\mathbb{Z}}_{p}^{\rm ur}\subset({{\mathbb{Q}}^{\rm cyc}})_{v}\) of \({\mathbb{Q}}_{p}^{\rm ur}\). It contains \({\mathbb{Z}}_{p}\) and \(\mu^{(p)}\). Note that the ring generated by \({\mathbb{Z}}\) and \(\mu^{(p)}\) is the ring of integers of the subfield \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) generated over \({\mathbb{Q}}\) by \(\mu^{(p)}\). One has the diagram of inclusions \({({{\mathbb{Q}}^{\rm cyc}})_{v}}\)\({{{\mathbb{Q}}^{\rm cyc}}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)oo\({\bar{\mathbb{F}}_{p}}\)\({{\mathbb{Z}}_{p}^{\rm ur}\ignorespaces\ignorespaces\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)OO\({\epsilon}\)oo\({{\mathbb{Z}}_{p}^{\rm ur}\cap{{\mathbb{Q}}^{\rm cyc}}\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)OOoo\({\mu^{(p)}\cup\{0\}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)oo\({{\mathbb{F}}_{p}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)OO\({{\mathbb{Z}}_{p}\ignorespaces\ignorespaces\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)\({\epsilon}\)ooOO\({{\mathbb{Z}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)OOoo\({\tau({\mathbb{F}}_{p})\ignorespaces\ignorespaces\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)OOoo (173) where \(\tau:{\mathbb{F}}_{p}\to{\mathbb{Z}}_{p}\) is the Teichmüller lift. Note that \(\tau({\mathbb{F}}_{p})\subset{\mathbb{Z}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\) since this lift is formed of roots of unity (of order \(p-1\)). In the middle line of the above diagram, the composite map \(\epsilon\) from \(\mu^{(p)}\cup\{0\}\) to \(\bar{\mathbb{F}}_{p}\) is an isomorphism of multiplicative monoids. Indeed, the Teichmüller lift \(\bar{\mathbb{F}}_{p}\ni x\mapsto\tau(x)\in{\mathbb{Z}}_{p}^{\rm ur}\) gives the inverse map. Since \(\bar{\mathbb{F}}_{p}\) is a field one can transport its additive structure using \(\epsilon\) and one obtains a unique element \(s_{v}\in\Sigma_{p}\). **Proposition 8.8****.**: _The map \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\ni v\mapsto s_{v}\in\Sigma_{p}\) is a bijection and is equivariant for the action of \(G_{p}={\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q}})\)._ Proof.: The action of \(G_{p}\) on the subset \(\mu^{(p)}\) is the one described in Lemma 8.6. This shows that the map \(v\mapsto s_{v}\) is equivariant. Since both spaces \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and \(\Sigma_{p}\) are homogeneous spaces over \(G_{p}\) with the same isotropy groups \(p^{\hat{\mathbb{Z}}}\subset G_{p}\) as follows from Lemmas 8.2 and 8.6, the map \(v\mapsto s_{v}\) is bijective. ∎ We can produce a concrete construction of the valuation \(v\) associated to the map \(s_{v}\). One first determines \(v\) on the subfield \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\). It is enough to determine the valuation \(v\) on elements of the form \[x=\sum n_{j}\xi_{j}\,,\ \ n_{j}\in{\mathbb{Z}}\,,\ \ \xi_{j}\in\mu^{(p)} \subset{{\mathbb{Q}}^{\rm cyc}}.\] Let \(K=\bar{\mathbb{F}}_{p}\) be the algebraic closure of \({\mathbb{F}}_{p}\) obtained by endowing the multiplicative monoid \(\mu^{(p)}\cup\{0\}\) with the addition associated to \(s_{v}\). One then has \[v(x)=w_{p}\left(\sum n_{j}\tau(\xi_{j})\right)\] (174) where \(w_{p}\) is the \(p\)-adic valuation in the Witt ring \({\mathbb{W}}_{p^{\infty}}(K)\) and \(\tau\) the Teichmüller lift. Finally since the field \({{\mathbb{Q}}^{\rm cyc}}\) is the composite of the subfields \({\mathbb{Q}}^{\rm cyc,p}\) and the fixed field of the action of \(G_{p}\subset\hat{\mathbb{Z}}^{*}={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q }})\) which is generated by roots of unity of order a \(p\)-power, one can use (166) to extend the valuation \(v\) uniquely to \({{\mathbb{Q}}^{\rm cyc}}\). [FIGURE:S8.F1][ENDFIGURE] We are now ready to complete the proof of Theorem 8.7, _i.e._ we prove that: **Lemma 8.9****.**: _An element \(s\in\Sigma_{p}\) is entirely characterized by a sequence \(P_{n}(T)\) of polynomials of \({\mathbb{F}}_{p}[T]\) fulfilling the Conway conditions as in Theorem 8.7._ Proof.: Let \(s\in\Sigma_{p}\). For each \(n\in{\mathbb{N}}\), let \({\mathbb{K}}_{n}(s)\) be the corresponding field structure on the union \(\{0\}\cup\mu^{(p)}(n)\), where \(\mu^{(p)}(n)\) is the group of roots of unity of order \(p^{n}-1\) in \({{\mathbb{Q}}^{\rm cyc}}\) generated by \(\xi=e(\frac{1}{p^{n}-1})\). The \({\mathbb{F}}_{p}\) vector space \({\mathbb{K}}_{n}(s)\) is of dimension \(n\) since its cardinality is \(p^{n}\). The canonical generator \(\xi\) of \(\mu^{(p)}(n)\) acts on the \({\mathbb{F}}_{p}\) vector space \({\mathbb{K}}_{n}(s)\) by the multiplication \(M_{\xi}\). We let \(P_{n}(T)\) be its characteristic polynomial _i.e._ the determinant \(P_{n}(T)=\det(T-M_{\xi})\). It is a monic polynomial of degree \(n\) with coefficients in \({\mathbb{F}}_{p}\). In the field \({\mathbb{K}}_{n}(s)\) one has \(P_{n}(\xi)=0\), since \(M_{\xi}\) fulfills its characteristic equation. Thus we derive a homomorphism of algebras \(\rho:{\mathbb{F}}_{p}[T]/(P_{n}(T))\to{\mathbb{K}}_{n}(s)\) which sends \(T\mapsto\xi\). It is surjective since any non-zero element of \({\mathbb{K}}_{n}(s)\) is a power of \(\xi\). Since \(P_{n}(T)\) has degree \(n\), the two algebras have the same dimension over \({\mathbb{F}}_{p}\) and thus \(\rho\) is an isomorphism. It follows that \(P_{n}(T)\) is irreducible over \({\mathbb{F}}_{p}\). The second property of \(P_{n}(T)\) also follows, since \(\xi\) is a generator of the multiplicative group. Now let \(m|n\) be a divisor of \(n\). Then \(r=p^{m}-1\) divides \(k=p^{n}-1\) and the group \(\mu^{(p)}(m)\) is a subgroup of \(\mu^{(p)}(n)\). Thus one has a field inclusion \({\mathbb{K}}_{m}(s)\subset{\mathbb{K}}_{n}(s)\), where the canonical generator \(\xi_{m}=e(\frac{1}{p^{m}-1})\) of \({\mathbb{K}}_{m}(s)\) is sent to \(\xi_{n}^{d}\), where \(\xi_{n}\) is the canonical generator \(\xi_{n}=e(\frac{1}{p^{n}-1})\) of \({\mathbb{K}}_{n}(s)\) and \(d=(p^{n}-1)/(p^{m}-1)\). One has \(P_{m}(\xi_{m})=0\) and hence \(P_{m}(\xi_{n}^{d})=0\) so that, using the above isomorphism \(\rho\), it follows that the polynomial \(P_{m}(T^{d})\) is a multiple of \(P_{n}(T)\). Conversely, given a sequence \(P_{n}(T)\) of polynomials fulfilling the conditions of the theorem, one constructs an algebraic closure \(\bar{\mathbb{F}}_{p}\) and an isomorphism \[\bar{\mathbb{F}}_{p}^{*}\stackrel{{ j}}{{\longrightarrow}}\mu^{(p)}\] as follows. One lets for each \(n\), \({\mathbb{K}}_{n}={\mathbb{F}}_{p}[T]/(P_{n}(T))\) and one gets an inductive system using for \(m|n\) the field homomorphism which sends the generator \(T_{m}\) of \({\mathbb{K}}_{m}\) to \(T_{n}^{d}\), \(d=(p^{n}-1)/(p^{m}-1)\). The inductive limit \({\mathbb{K}}=\varinjlim{\mathbb{K}}_{n}\) is an algebraic closure \(\bar{\mathbb{F}}_{p}\) of \({\mathbb{F}}_{p}\) and the map \(T_{n}\mapsto e^{2\pi i/k}\), \(k=p^{n}-1\), defines an isomorphism \(j\) of \(\bar{\mathbb{F}}_{p}^{*}\) with \(\mu^{(p)}\). Note that this construction makes sense also for \(n=1\) and that the first polynomial is of degree one and thus picks a specific generator of the multiplicative group of \({\mathbb{F}}_{p}\). One checks that the sequence of polynomials associated to the pair \((\bar{\mathbb{F}}_{p},j)\) is the sequence \(P_{n}(T)\). Thus there is a complete equivalence between elements \(s\in\Sigma_{p}\) and sequences of polynomials fulfilling the Conway conditions of the Theorem. ∎ To make the above map from \(\Sigma_{p}\) to sequences of polynomials more explicit we introduce the “trace invariant” of an element \(s\in\Sigma_{p}\). We continue to denote by \({\mathbb{K}}_{n}(s)\) the field structure on the union \(\{0\}\cup\mu^{(p)}(n)\), where \(\mu^{(p)}(n)\) is the group of roots of unity generated by \(\xi=e(\frac{1}{p^{n}-1})\). In particular, \({\mathbb{K}}_{1}(s)\) is a field uniquely isomorphic to \({\mathbb{F}}_{p}\). Let \(\eta\in\mu^{(p)}\), then the orbit \({\mathcal{O}}=\{{\rm Fr}^{k}(\eta)\mid k\in{\mathbb{N}}\}\) of the map \(x\mapsto{\rm Fr}(x)=x^{p}\) is a finite set, let \(|{\mathcal{O}}|\) be its cardinality. Then the following sum \[{\rm tr}_{s}({\mathcal{O}})=\sum_{{\mathcal{O}}}\eta\] (175) computed in any \({\mathbb{K}}_{n}(s)\), for \(|{\mathcal{O}}||n\) is the same and determines an element of \({\mathbb{K}}_{1}(s)={\mathbb{F}}_{p}\). **Definition 8.10****.**: _Let \({\mathbb{O}}(p)\) be the space of orbits of the map \(x\mapsto{\rm Fr}(x)=x^{p}\) acting on \(\mu^{(p)}\). Let \(s\in\Sigma_{p}\). We call the map_ \[{\rm tr}_{s}:{\mathbb{O}}(p)\to{\mathbb{F}}_{p}\,,\ \ {\mathcal{O}}\mapsto{\rm tr }_{s}({\mathcal{O}})\] (176) _the trace invariant of \(s\)._ The trace invariant characterizes \(s\) as shown by the next Proposition. **Proposition 8.11****.**: _Let \(s\in\Sigma_{p}\). Then for each \(n\in{\mathbb{N}}\) the polynomial \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\) associated to \(s\) by Lemma 8.9 is given by_ \[P_{n}(T)=T^{n}+\sum_{k=1}^{n-1}(-1)^{k}\sigma_{k}T^{n-k}\] (177) _for_ \[\sigma_{k}=\sum_{{\mathcal{O}}\subset D_{k}}{\rm tr}_{s}({\mathcal{O}}),\] (178) _where \(D_{k}\subset{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) is the set of fractions \(\frac{a}{p^{n}-1}\) where \(1\leq a\leq p^{n}-1\) and the digits of \(a\) in base \(p\) are all zeros except for \(k\) of them which are equal to \(1\)._ Proof.: In the field \({\mathbb{K}}_{n}(s)\) the \(n\) roots of the polynomial \(P_{n}(T)\) are the elements \(e(\frac{p^{j}}{p^{n}-1})\), for \(j=0,\ldots,n-1\). For each \(k=1,\ldots,n\), the set of products of \(k\) distinct roots is the set of elements of the form \[e\left(\sum_{j\in Y}\frac{p^{j}}{p^{n}-1}\right)\,,\ \ Y\subset\{0,1,\ldots,n- 1\}\,,\ |Y|=k.\] One thus gets that the \(k\)-th symmetric function \(\sigma_{k}\) of the roots of \(P_{n}(T)\) is given by the sum (178), over orbits \({\mathcal{O}}\) satisfying the prescribed condition \({\mathcal{O}}\subset D_{k}\).∎ We now give a third equivalent description of the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). We recall that the decomposition subfield \({\mathbb{Q}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\) is independent of the choice of \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and is equal to \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{{\mathbb{Q}}^{\rm cyc}}\). **Proposition 8.12****.**: _The map_ \[\beta:{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\to{\mbox{Hom}}({{\mathbb{Q}}^{ \rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p}),\qquad\beta(v)=\beta_{v}:{{\mathbb{Q}}^ {\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}_{p}\] _where the fields inclusion \(\beta_{v}\) derives from (165), determines a canonical and equivariant isomorphism of sets._ Proof.: Notice that the inclusion \(\beta_{v}:{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}_{p}\) depends upon the choice of the valuation \(v\). One has \(\beta_{v}\in{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) and the map \(v\mapsto\beta_{v}\) is equivariant for the action of \(G_{p}/f_{p}^{\hat{\mathbb{Z}}}\) on \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and on the space \({\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) by \[{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\ni\beta \mapsto\beta\circ\gamma\,,\quad~{}\forall\gamma\in G_{p}={\rm Gal}({\mathbb{Q} }^{\rm cyc,p}:{\mathbb{Q}}).\] (179) Since for both spaces the action of \(G_{p}/f_{p}^{\hat{\mathbb{Z}}}\) is free and transitive, it follows that the map \(\beta\) is bijective. ∎ We let \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) be the group ring of \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) and let \({\rm Fr}\in{\rm Aut}({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}])\) be the Frobenius automorphism given by the natural linearization of the group automorphism \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), of multiplication by \(p\) (_cf._ Corollary 2.4). The natural ring homomorphism \[\delta:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Q}}^{\rm cyc ,p}\] (180) is equivariant for the action of \({\rm Fr}\), its image is the subring of integers of \({\mathbb{Q}}^{\rm cyc,p}\) while the kernel is described by the intersection \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\cap J\), where \(J\) is the ideal of Definition 8.1. The \({\mathbb{F}}_{p}\)-algebra \[{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\otimes_{\mathbb{Z}}{\mathbb{ F}}_{p}={\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\] (181) is perfect since the group \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) is uniquely \(p\)-divisible. By restriction to the fixed points of \({\rm Fr}\) and composition with the residue map \(\epsilon:{\mathbb{Z}}_{p}\to{\mathbb{F}}_{p}\), one obtains the map \[{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\to{\mbox{ Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr},{\mathbb{ F}}_{p}),\quad\alpha\mapsto{\rm res}(\alpha)=\epsilon\circ\alpha\circ\delta.\] (182) Note that elements of \({\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr},{ \mathbb{F}}_{p})\) are finitely supported maps from \({\mathbb{O}}(p)\) to \({\mathbb{F}}_{p}\), thus they can be lifted to elements of \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\). One derives \[{\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}={\mathbb{Z}}[{( {\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\otimes_{\mathbb{Z}}{\mathbb{F}}_{p}.\] Next, we show that the map res as in (182) is injective. **Proposition 8.13****.**: _Let \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). We denote by \(s_{v}\in\Sigma_{p}\) and \(\beta_{v}:{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\to{\mathbb{Q}}_{p}\) the corresponding elements as in Lemma 8.8 and Proposition 8.12. Then the trace invariant map of \(s_{v}\) has the following description_ \[{\rm tr}_{s_{v}}={\rm res}(\beta_{v}).\] (183) _The map \({\rm res}\) as in (182) is injective._ Proof.: The additive structure \(s_{v}\) on \({{\mathcal{M}}{(p)}}=\{0\}\cup\mu^{(p)}\) is the same as that of the residue field of the completion \({\mathbb{Q}}^{\rm cyc,p}\) for the restriction of \(v\). It follows that on each orbit \({\mathcal{O}}\) of the action of \({\rm Fr}\) on \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), the sum \({\rm tr}_{s_{v}}({\mathcal{O}})\) coincides with the residue \[\epsilon(\beta_{v}(u))\,,\ \ u=\sum_{\mathcal{O}}\xi\in{{\mathbb{Q}}^{\rm cyc, p}_{\rm Fr}}.\] Since \(u=\delta(w)\) where \(w=\sum_{\mathcal{O}}\xi\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{ \rm Fr}\) one gets (183). Then, it follows from Proposition 8.11 that the map \({\rm res}\) is injective.∎ We now briefly explain how one can reconstruct \(\alpha\in{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) from its residue \({\rm res}(\alpha)\), using the Witt functor \({\mathbb{W}}_{p^{\infty}}\). Given \(\varsigma\in{\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] ^{\rm Fr},{\mathbb{F}}_{p})\), the Witt functor \({\mathbb{W}}_{p^{\infty}}\) yields a homomorphism \[{\mathbb{W}}_{p^{\infty}}(\varsigma)\in{\mbox{Hom}}({\mathbb{W}}_{p^{\infty}}( {\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}),{\mathbb{Z}}_{ p}).\] (184) If \(\varsigma={\rm res}(\alpha)\), one can reconstruct \(\alpha\) directly using \({\mathbb{W}}_{p^{\infty}}(\varsigma)\). This gives a direct proof of the injectivity of the map \({\rm res}\). Indeed, for an orbit \({\mathcal{O}}\) of the action of \({\rm Fr}\) on \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), the element (\(\tau=\) Teichmüller lift) \[\nu({\mathcal{O}})=\sum_{\mathcal{O}}\tau(\upsilon)\in{\mathbb{W}}_{p^{\infty} }({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}])\] is fixed by the Frobenius, _i.e._\(\nu({\mathcal{O}})\in{\mathbb{W}}_{p^{\infty}}({\mathbb{F}}_{p}[{({\mathbb{Q}} /{\mathbb{Z}})^{(p)}}]^{\rm Fr})\). One then sees that \[\alpha\left(\sum_{\mathcal{O}}\upsilon\right)={\mathbb{W}}_{p^{\infty}}( \varsigma)(\nu({\mathcal{O}}))\,.\] (185) We end this section by giving the relation between \(\Sigma_{p}={\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and the space \(X_{p}\) of all injective group homomorphisms \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to({{\mathbb{Q}}^{\rm cyc}})^{\times}\) (_cf._ Definition 4.3). We recall that the Galois group \({\rm Aut}(\bar{\mathbb{F}}_{p})\) is the closure \(f_{p}^{\hat{\mathbb{Z}}}\) of the group generated by the Frobenius \(f_{p}\). **Proposition 8.14****.**: _Let \(\bar{\mathbb{F}}_{p}\) be a fixed algebraic closure of \({\mathbb{F}}_{p}\). Then_ \((1)\)_\(G_{p}\) acts freely and transitively on \(X_{p}\)._ \((2)\) _The quotient of \(X_{p}\) by \(f_{p}^{\hat{\mathbb{Z}}}\) is isomorphic to \(\Sigma_{p}={\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\)._ Proof.: Let \(\sigma\in X_{p}\). The range of \(\sigma\) is the group \(\mu^{(p)}\) of all roots of unity in \({{\mathbb{Q}}^{\rm cyc}}\) of order prime to \(p\). Thus for a pair \(\sigma_{j}\in X_{p}\), \(j=1,2\), one has \(\sigma_{1}\circ\sigma_{2}^{-1}\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}} )=G_{p}\). This proves the first statement. For any isomorphism \(\sigma:\bar{\mathbb{F}}_{p}^{*}\stackrel{{}}{{\longrightarrow}}({{ \mathbb{Q}}^{\rm cyc}})^{\times}\) of the multiplicative group of the algebraic closure \(\bar{\mathbb{F}}_{p}\) with the group \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), the following defines an element \(s\in\Sigma_{p}\), \[s(x)=\sigma(\sigma^{-1}(x)+1)\,,\quad~{}\forall x\neq-1\,,\ s(-1)=0.\] (186) All elements of \(\Sigma_{p}\) arise this way. Two pairs \((\bar{\mathbb{F}}_{p},\sigma_{j})\), \(j=1,2\) whose associated \(s_{j}\in\Sigma_{p}\) are the same are easily seen to be related by an automorphism \(\theta\in{\rm Aut}(\bar{\mathbb{F}}_{p})\)_i.e._\(\sigma_{2}=\sigma_{1}\circ\theta\). The second statement thus follows.∎ Proposition 8.12 suggests a more appropriate equivalent description of \(X_{p}\) using a chosen algebraic closure \(\bar{\mathbb{Q}}_{p}\) of the \(p\)-adic field and its completion \({\mathbb{C}}_{p}\). **Corollary 8.15****.**: _The map_ \[i:X_{p}\to{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p}),\qquad\sigma \mapsto\tau\circ\sigma^{-1}\\] (187) _where \(\sigma^{-1}\) is composed with the Teichmüller lift to determine a field homomorphism from \({\mathbb{Q}}^{\rm cyc,p}\) to \({\mathbb{C}}_{p}\), is a bijection of sets._ _The canonical surjection \(X_{p}\to\Sigma_{p}\) of Proposition 8.14\((2)\) is the restriction map_ \[{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\to{\mbox{Hom}}({{ \mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p}).\] (188) Proof.: Let \(\sigma\in X_{p}\), then \(\sigma^{-1}:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to\bar{\mathbb{F}}_{p}^{\times}\) composed with the Teichmüller lift \(\tau:\bar{\mathbb{F}}_{p}^{\times}\to{\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^ {\rm ur}}}\subset{\mathbb{C}}_{p}\) extends to a unique homomorphism \(i(\sigma)\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\). The map \(i\) is equivariant for the action of \(G_{p}\) on \(X_{p}\) as in Proposition 8.14 and on \({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\) by composition with elements of \(G_{p}={\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q}})\). Since both actions are free and transitive, \(i\) is bijective. For any \(\gamma\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\), the range of \(\gamma\) is the subfield of the maximal unramified extension \({\mathbb{Q}}_{p}^{\rm ur}\subset{\mathbb{C}}_{p}\) generated over \({\mathbb{Q}}\) by roots of unity of order prime to \(p\). One has by construction \(\gamma\circ{\rm Fr}={\rm Fr}_{p}\circ\gamma\). Thus the image \(\gamma({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}})\) is contained in the fixed subfield \({\mathbb{Q}}_{p}\) for the action of \({\rm Fr}_{p}\) on \({\mathbb{Q}}_{p}^{\rm ur}\). This shows that the restriction map (188) is well defined. For \(j=1,2\), let \(\gamma_{j}\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\), then \(\gamma_{2}^{-1}\circ\gamma_{1}\in{\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q }})\) and this automorphism fixes \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\) pointwise if and only the restrictions \(\gamma_{j}|_{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\) are equal. Since \({\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}})\) is topologically generated by \({\rm Fr}\), this happens if and only if the \(\gamma_{j}\) are the same in the quotient of \(X_{p}\) by \(f_{p}^{\hat{\mathbb{Z}}}\).∎ We implement the homomorphism \(\delta:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Q}}^{\rm cyc ,p}\) of (180) to associate to an element \(\rho\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\) its residue \[{\rm res}(\rho)=\epsilon\circ\rho\circ\delta\in{\mbox{Hom}}({\mathbb{F}}_{p}[{ ({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}],\bar{\mathbb{F}}_{p}).\] (189) The image of \(\delta\) is the ring of integers of \({\mathbb{Q}}^{\rm cyc,p}\), thus the image of \(\rho\circ\delta\) in \({\mathbb{C}}_{p}\) is contained in \({\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\) and the composite \(\epsilon\circ\rho\circ\delta\) is well defined. Moreover, since \(\text{Ker}(\delta)=J\cap{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\), it follows that \(\text{Ker}({\rm res}(\rho))\) contains the ideal \(J_{p}\) reduction of \(\text{Ker}(\delta)\) modulo \(p\). **Proposition 8.16****.**: _Let \({{\mathcal{A}}}\) be the quotient algebra \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]/J_{p}\). Then_ \((1)\) _The map_ \[{\rm res}:{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\to{\mbox{Hom }}({{\mathcal{A}}},\bar{\mathbb{F}}_{p}),\qquad{\rm res}(\rho)=\epsilon\circ \rho\circ\delta\] (190) _is a bijection of sets._ \((2)\) _The algebraic spectrum \({\rm Spec\,}({{\mathcal{A}}})\) is in canonical bijection with the set \(\Sigma_{p}\)._ \((3)\) _The canonical surjection \(X_{p}\to\Sigma_{p}\) of Proposition 8.14\((2)\) corresponds to the natural map_ \[{\mbox{Hom}}({{\mathcal{A}}},\bar{\mathbb{F}}_{p})\to{\rm Spec\,}({{\mathcal{A }}}).\] (191) Proof.: \((1)\) For any integer \(m\) prime to \(p\), the ideal \(J_{p}\) contains the projection (_cf._ Definition 8.1) \(\pi_{m}=\frac{1}{m}\sum_{j=0}^{m-1}e(\frac{j}{m})\). Thus an element \(\rho\in{\mbox{Hom}}({{\mathcal{A}}},\bar{\mathbb{F}}_{p})\) is given by a group homomorphism \(\rho:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to\bar{\mathbb{F}}_{p}^{\times}\) such that (for \(m>1\) prime to \(p\)) \(\sum_{j=0}^{m-1}\rho(e(\frac{j}{m}))=0\). Notice that this equality holds if and only if \(\rho\) is injective and hence, by restriction to the finite level subgroups in the projective limit \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), if and only if it is bijective. Thus \((1)\) follows from the first statement of Corollary 8.15. \((2)\) Consider the finite field \({\mathbb{F}}_{p^{n}}\). Two generators of the multiplicative group \({\mathbb{F}}_{p^{n}}^{\times}\) have the same characteristic polynomial if and only if they are conjugate under the action of the Galois group \(\text{Gal}({\mathbb{F}}_{p^{n}}:{\mathbb{F}}_{p})\). This shows that the cardinality of the set \(I_{n}\) of irreducible primitive polynomials of degree \(n\) over \({\mathbb{F}}_{p}\) is \(\varphi(p^{n}-1)/n\), where \(\varphi\) is the Euler totient function. Each of these polynomials \(P(X)\) divides the reduction modulo \(p\) of the cyclotomic polynomial \(\Phi_{p^{n}-1}(X)\), thus one derives, modulo \(p\), the following equality \[\Phi_{p^{n}-1}(X)=\prod_{I_{n}}P(X)\] (192) since the degrees of the polynomials are the same and the right hand side divides the left one. Moreover one also has \[\Phi_{p^{n}-1}\left(e(\frac{1}{p^{n}-1})\right)\in J_{p}\,.\] This determines a canonical isomorphism \[{{\mathcal{A}}}_{n}={\mathbb{F}}_{p}[\mu^{(p)}(n)]/(J_{p}\cap{\mathbb{F}}_{p}[ \mu^{(p)}(n)])\to\prod_{I_{n}}{\mathbb{F}}_{p^{n}}\] (193) and thus a canonical bijection of sets \({\rm Spec\,}({{\mathcal{A}}}_{n})\to I_{n}\). Since \({{\mathcal{A}}}\) is the inductive limit of the \({{\mathcal{A}}}_{n}\), \({\rm Spec\,}({{\mathcal{A}}})\) is the projective limit of the \(I_{n}\), _i.e._ the space of sequences of Conway polynomials as in Theorem 8.7. This space is in canonical bijection with \(\Sigma_{p}\). \((3)\) follows from the proof of \((2)\). ∎ The restriction to the fixed points of the Frobenius automorphism \({\rm Fr}\in{\rm Aut}({{\mathcal{A}}})\) does not change the algebraic spectrum as a set, thus we derive a canonical bijection of sets \[{\rm Spec\,}({{\mathcal{A}}})\stackrel{{\sim}}{{\to}}{\rm Spec\,}( {{\mathcal{A}}}^{\rm Fr}).\] (194) Finally, we characterize the image of the map \({\rm res}\) as in (182). **Corollary 8.17****.**: _Let \(\varsigma\in{\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] ^{\rm Fr},{\mathbb{F}}_{p})\). Then \(\varsigma\) belongs to the image of the map \({\rm res}\) as in (182) if and only if \(\text{Ker}(\varsigma)\) contains \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\cap J_{p}\)._ Proof.: By (194), and Proposition 8.16, \((2)\), one has natural bijections of sets \[\Sigma_{p}\simeq{\rm Spec\,}({{\mathcal{A}}})\simeq{\rm Spec\,}({{\mathcal{A}} }^{\rm Fr})\simeq{\mbox{Hom}}({{\mathcal{A}}}^{\rm Fr},{\mathbb{F}}_{p}).\] Then, the statement follows by noticing that the elements of \({\mbox{Hom}}({{\mathcal{A}}}^{\rm Fr},{\mathbb{F}}_{p})\) are the elements of \({\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr},{ \mathbb{F}}_{p})\) whose kernel contains \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\cap J_{p}\).∎ ## 9. The base point problem and the “curve” for the global field \({\mathbb{Q}}\) In this section we compare the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) of extensions of the \(p\)-adic valuation to \({{\mathbb{Q}}^{\rm cyc}}\) (studied at length in section 8), with the fiber over a prime \(p\) of a space \(Y\) which represents, in this set-up, the analogue of the curve that, for function fields, plays a fundamental role in A. Weil’s proof of the Riemann Hypothesis. Our results show that for each place \(v\in\Sigma({\mathbb{Q}})\), there is a natural model \(Y_{v}\) for the fiber over \(v\) and an embedding of this model in a noncommutative space \(X({\mathbb{C}}_{v})\) which is a \(v\)-adic avatar of the adèle class space \({\mathbb{H}}_{\mathbb{Q}}={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}\). We shall denote by \({\mathbb{K}}\) a global field. To motivate our constructions we first recall a few relevant facts holding for function fields. ### Adelic interpretation of the loop groupoid \(\Pi_{1}^{\rm ab}(X)^{\prime}\) for function fields In this subsection we assume that \({\mathbb{K}}\) is a function field. We let \({\mathbb{F}}_{q}\subset{\mathbb{K}}\) be the field of constants. Let \(\bar{\mathbb{K}}\) be a fixed separable closure of \({\mathbb{K}}\) and let \({\mathbb{K}}^{\rm ab}\subset\bar{\mathbb{K}}\) be the maximal abelian extension of \({\mathbb{K}}\). We denote by \(\bar{\mathbb{F}}_{q}\) the algebraic closure of the finite field \({\mathbb{F}}_{q}\) inside \({\mathbb{K}}^{\rm ab}\). A main result holding for function fields is that for each finite field extension \(E\) of \(\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}}\) the space of (discrete) valuations \({\rm Val}(E)\) inherits the structure of an algebraic, one-dimensional scheme \(X_{E}\) whose non-empty open sets are the complements of the finite subsets and whose structure sheaf is defined by considering the intersection of the valuation rings inside \(E\). More precisely, \({\rm Val}(E)\) coincides with the set of (closed) points of the unique projective, nonsingular algebraic curve \(X_{E}\) with function field \(E\). We recall (_cf._[21] Corollary 6.12) that the category of nonsingular, projective algebraic curves and dominant morphisms is equivalent to the category of function fields of dimension one over \(\bar{\mathbb{F}}_{q}\). Thus, one associates (uniquely) to \({\mathbb{K}}^{\rm ab}=\varinjlim_{E}E\) the projective limit \(X^{\rm ab}=\varprojlim_{E}X_{E}\) which is the abelian cover \(X^{\rm ab}\to X\) of the non singular projective curve \(X\) over \({\mathbb{F}}_{q}\) with function field \({\mathbb{K}}\). By restricting valuations, one also derives a natural projection map \[\pi:X^{\rm ab}={\rm Val}({\mathbb{K}}^{\rm ab})\to\Sigma({\mathbb{K}})\] onto the space \(\Sigma({\mathbb{K}})\) of valuations of \({\mathbb{K}}\). Thus, in the function field case one derives a geometric interpretation for the natural fibration associated to the space of valuations of the field extension \({\mathbb{K}}^{\rm ab}\supset{\mathbb{K}}\). In [13] we have given an adelic description of the loop groupoid \(\Pi_{1}^{\rm ab}(X)^{\prime}\) of the abelian cover \(X^{\rm ab}\to X\). We recall that the adèle class space \({\mathbb{A}}_{\mathbb{K}}/{\mathbb{K}}^{*}\) of any global field \({\mathbb{K}}\) has a natural structure of hyperring \({\mathbb{H}}_{\mathbb{K}}\) (_cf._[13]) and that the prime elements \(P({\mathbb{H}}_{\mathbb{K}})\) of this hyperring determine a groupoid. The units of this groupoid form the set \(\Sigma({\mathbb{K}})\) of places of \({\mathbb{K}}\) and the source and range maps coincide with the map \[s:P({\mathbb{H}}_{\mathbb{K}})\to\Sigma({\mathbb{K}})\] which associates to a prime element of \({\mathbb{H}}_{\mathbb{K}}\) the principal prime ideal of \({\mathbb{H}}_{\mathbb{K}}\) it generates (and thus the associated place). When \({\mathbb{K}}\) is a function field, the groupoid \(P({\mathbb{H}}_{\mathbb{K}})\) is canonically isomorphic to the loop groupoid \(\Pi_{1}^{\rm ab}(X)^{\prime}\) of the abelian cover \(X^{\rm ab}\to X\), and the isomorphism is equivariant for the respective actions of the abelianized Weil group \({\mathcal{W}}^{\rm ab}\) (_i.e._ the subgroup of elements of \({\rm Gal}({\mathbb{K}}^{\rm ab}:{\mathbb{K}})\) whose restriction to \(\bar{\mathbb{F}}_{q}\) is an integral power of the Frobenius), and of the idèle class group \(C_{\mathbb{K}}={\mathbb{A}}_{\mathbb{K}}^{*}/{\mathbb{K}}^{*}\). It follows that, as a group action on a set, the action of \({\mathcal{W}}^{\rm ab}\) on \({\rm Val}({\mathbb{K}}^{\rm ab})\) is isomorphic to the action of the idèle class group \(C_{\mathbb{K}}\) on \(P({\mathbb{H}}_{\mathbb{K}})\). In other words, by choosing a set theoretic section \(\xi\) of the projection \[\pi\;:\;{\rm Val}({\mathbb{K}}^{\rm ab})\to\Sigma({\mathbb{K}})\,,\ \ \pi(v)=v |_{\mathbb{K}},\] (195) one obtains an equivariant set theoretic bijection \(P({\mathbb{H}}_{\mathbb{K}})\simeq_{\xi}{\rm Val}({\mathbb{K}}^{\rm ab})\) which depends though, in a crucial manner, on the choice of the base point \(\xi(w)\), for each place \(w\in\Sigma({\mathbb{K}})\). This dependence prevents one from transporting the algebraic geometric structure of \(X^{\rm ab}\) onto \(P({\mathbb{H}}_{\mathbb{K}})\), and it also shows that the adelic space \(P({\mathbb{H}}_{\mathbb{K}})\) carries only the information on the curve \(X^{\rm ab}\) given in terms of a set with a group action. ### Fiber over a finite place of \({\mathbb{Q}}\) Now, we turn to the global field \({\mathbb{K}}={\mathbb{Q}}\). A natural starting point for the construction of a replacement of the covering \(X^{\rm ab}\) in this number field case is to consider the maximal abelian extension of \({\mathbb{Q}}\), _i.e._ the cyclotomic field \({{\mathbb{Q}}^{\rm cyc}}\) as analogue of \({\mathbb{K}}^{\rm ab}\). Then, the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) of extensions of the \(p\)-adic valuation to \({{\mathbb{Q}}^{\rm cyc}}\) appears as the first candidate for the analogue of the fiber, over a finite place, of the abelian cover \(X^{\rm ab}\to X\). Thus, the first step is evidently that to compare \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) with the fiber \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) of the fibration \(s:P({\mathbb{H}}_{\mathbb{Q}})\to\Sigma({\mathbb{Q}})\) over a rational prime \(p\in\Sigma({\mathbb{Q}})\). At the level of sets with group actions, this process shows that \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) is not yet the correct fiber. The following discussion indicates that one should consider instead the total space of a principal bundle, with base \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and structure group a connected compact solenoid \(S\) whose definition is given in Proposition 9.2. Then, a natural construction of the fiber is provided by the mapping torus \(Y_{p}\) of the action of the Frobenius on the space \(X_{p}\) of Definition 4.3. **Proposition 9.1****.**: _Let \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) be the fiber of the groupoid \(P({\mathbb{H}}_{\mathbb{Q}})\) over a non-archimedean, rational prime \(p\in\Sigma_{\mathbb{Q}}\). Then, the following results hold._ \((1)\) _The idèle class group \(C_{\mathbb{Q}}={\mathbb{A}}^{*}_{\mathbb{Q}}/{\mathbb{Q}}^{*}\) acts transitively on \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\). The isotropy group of any element of \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) is the cocompact subgroup \(W_{p}={\mathbb{Q}}_{p}^{*}\subset C_{\mathbb{Q}}\) of classes of idèles \((j_{v})\) such that \(j_{v}=1\), \(\forall v\neq p\)._ \((2)\) _Under the class field theory isomorphism_ \[{\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\simeq C_{\mathbb{Q}}/D_{ \mathbb{Q}}\,,\ \ D_{\mathbb{Q}}=\text{connected component of}\;1,\] (196) \(C_{\mathbb{Q}}\) _acts transitively on \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) and the isotropy group of any element of \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) is_ \[I_{p}={\mathbb{Z}}_{p}^{*}\times H\times{\mathbb{R}}_{+}^{*}\subset\hat{ \mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}=C_{\mathbb{Q}}.\] (197) \(H\subset G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) _is the closed subgroup \(p^{\hat{\mathbb{Z}}}\subset G_{p}\) generated by \(p\) in \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\)._ Proof.: \((1)\) follows from Theorem 7.10 of [13]. \((2)\) follows from Lemma 8.2. ∎ Notice that if \({\mathbb{K}}\) is a function field and \(v\) is a valuation of \({\mathbb{K}}^{\rm ab}\) extending the valuation \(w\) of \({\mathbb{K}}\), any \(g\in{\mathcal{W}}^{\rm ab}\subset{\rm Gal}({\mathbb{K}}^{\rm ab}:{\mathbb{K}})\) such that \(g(v)=v\), belongs to the local Weil group \({\mathcal{W}}^{\rm ab}_{w}\subset{\mathcal{W}}^{\rm ab}\). This is due to the fact that the restriction of \(g\) to an automorphism of \(\bar{\mathbb{F}}_{q}\) is an integral power of the Frobenius. When \({\mathbb{K}}={\mathbb{Q}}\), the isotropy group of the valuation \(v\) is instead larger than the local Weil group \(W_{p}\). The difference is determined by the presence of the quotient \(I_{p}/W_{p}\) of the isotropy group \(I_{p}\) by the local Weil group \(W_{p}={\mathbb{Q}}_{p}^{*}={\mathbb{Z}}_{p}^{*}\times(\tilde{p})^{\mathbb{Z}}\). Here, \(\tilde{p}\) is represented by the idèle all of whose components are \(1\) except at the place \(p\) where it is equal to \(p^{-1}\). By multiplying with the principal idèle \(p\), one gets the same class as the element of \(\hat{\mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}\) which is equal to \(p\) everywhere except at the place \(p\) where it is equal to \(1\). Thus, its image in \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) is \(p\). The quotient group \[I_{p}/W_{p}=(H\times{\mathbb{R}}_{+}^{*})/(\tilde{p})^{\mathbb{Z}}\simeq(\hat{ \mathbb{Z}}\times{\mathbb{R}})/{\mathbb{Z}}=S\] (198) is a compact connected solenoid which is described in the following Proposition 9.2. The presence of the connected piece \(S\) is due to the fact that the connected component of the identity in the idèle class group acts trivially, at the Galois level, on \({{\mathbb{Q}}^{\rm cyc}}\). **Proposition 9.2****.**: _The group \(S\) is compact and connected and is canonically isomorphic to the projective limit of the compact groups \({\mathbb{R}}/n{\mathbb{Z}}\), under divisibility of the labels \(n\)._ Proof.: We consider first the factor \[S_{n}=(({\mathbb{Z}}/n{\mathbb{Z}})\times{\mathbb{R}})/{\mathbb{Z}}\] of the projective limit \(S\), where \({\mathbb{Z}}\) acts diagonally, _i.e._ by the element \((1,1)\), on \(({\mathbb{Z}}/n{\mathbb{Z}})\times{\mathbb{R}}\). One has a natural map \(p_{n}:S_{n}\to{\mathbb{R}}/n{\mathbb{Z}}\) given by \[p_{n}(j,s)=s-j\,,\quad~{}\forall s\in{\mathbb{R}},\ j\in{\mathbb{Z}}/n{\mathbb {Z}},\] where one views \({\mathbb{Z}}/n{\mathbb{Z}}\) as a subgroup of \({\mathbb{R}}/n{\mathbb{Z}}\). The map \(p_{n}\) is an isomorphism of groups. When \(n\) divides \(m\), the subgroup \(m{\mathbb{Z}}\subset{\mathbb{Z}}\) is contained in \(n{\mathbb{Z}}\subset{\mathbb{Z}}\) and this inclusion corresponds to the projection \({\mathbb{Z}}/m{\mathbb{Z}}\to{\mathbb{Z}}/n{\mathbb{Z}}\). Under the isomorphisms \(p_{n}\), this corresponds to the projection \({\mathbb{R}}/m{\mathbb{Z}}\to{\mathbb{R}}/n{\mathbb{Z}}\). Thus the projective system defining \(S\) is isomorphic to the projective system of the projections \({\mathbb{R}}/m{\mathbb{Z}}\to{\mathbb{R}}/n{\mathbb{Z}}\) and the projective limits are isomorphic.∎ Next, we describe a general construction of mapping torus which yields, when applied to the groups \[X=G_{p}\,,\ \ Z=G_{p}/p^{\hat{\mathbb{Z}}},\] (199) the fiber \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) of the groupoid \(P({\mathbb{H}}_{\mathbb{Q}})\) over a finite, rational prime \(p\in\Sigma({\mathbb{Q}})\). **Proposition 9.3****.**: _Let \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) be the group of automorphisms of the multiplicative group \(\mu^{(p)}\) of roots of unity in \({{\mathbb{Q}}^{\rm cyc}}\) of order prime to \(p\) and let \(f_{p}\in G_{p}\) be the element \(\xi\mapsto\xi^{p}\). Let \(G_{p}\) act freely and transitively on a compact space \(X\). Let \(Y\) be the quotient space_ \[Y=\left(X\times(0,1)\right)/\sigma^{\mathbb{Z}},\] (200) _where \(\sigma^{\mathbb{Z}}\) acts on the product \(X\times(0,1)\) as follows_ \[\sigma(x,\rho)=(f_{p}x,\rho^{p})\,,\quad~{}\forall x\in X,\ \rho\in(0,1).\] (201) _Then, the following results hold._ \((1)\) _The space \(Y\) is compact and is an \(S\)-principal bundle over the quotient \(Z\) of \(X\) by \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\), where \(S\) is the solenoid group of Proposition 9.2._ \((2)\) _Let \(X\) and \(Z\) be as in (199), then \(Y\) is canonically isomorphic to the fiber \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\)._ Proof.: \((1)\) We first look at the action of \({\mathbb{Z}}\) on the open interval \((0,1)\) given by \(\rho\mapsto\rho^{p}\). We consider the map \(\psi:(0,1)\to{\mathbb{R}}\) given by \[\psi(\rho)=\log(-\log(\rho))\,,\quad~{}\forall\rho\in(0,1).\] (202) One has \[\psi(\rho^{p})=\log(-\log(\rho^{p}))=\log(-p\log(\rho))=\log(-\log(\rho))+\log (p)=\psi(\rho)+\log(p)\] which shows that the action of \({\mathbb{Z}}\) on \((0,1)\) given by \(\rho\mapsto\rho^{p}\) is isomorphic to the action of \({\mathbb{Z}}\) on \({\mathbb{R}}\) given by translation by \(\log(p)\). By construction \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) is a compact, totally disconnected group. Next, we show that the map which associates to \(n\in{\mathbb{Z}}\) the element \(f_{p}^{n}\in G_{p}\) extends to a bijection of \(\hat{\mathbb{Z}}\) with the closed subgroup of \(G_{p}\) generated by \(f_{p}\). In fact, the isomorphism follows from the isomorphism between \(G_{p}\) and \(\text{Gal}(\bar{\mathbb{F}}_{p}:{\mathbb{F}}_{p})\), with \(f_{p}\) being the Frobenius. The result follows by applying _e.g._[5] (Chapitre V, Appendice II, Exercice 5). This gives a natural inclusion \(\hat{\mathbb{Z}}\subset G_{p}\), \(a\mapsto f_{p}^{a}\), as a closed subgroup. We now consider the action of the product group \(\hat{\mathbb{Z}}\times{\mathbb{R}}_{+}^{*}\) on \(X\times(0,1)\) given by \[(a,\lambda).(x,\rho)=(f_{p}^{a}\,x,\rho^{\lambda}).\] (203) By construction the element \((1,p)\in\hat{\mathbb{Z}}\times{\mathbb{R}}_{+}^{*}\) acts as \(\sigma\) (_cf._ (201)). The quotient group \[(\hat{\mathbb{Z}}\times{\mathbb{R}}_{+}^{*})/s^{\mathbb{Z}}\,,\ \ s=(1,p)\] (204) is isomorphic to the solenoid \(S\), by using the isomorphism of the group \({\mathbb{R}}_{+}^{*}\) with \({\mathbb{R}}\) given by the logarithm in base \(p\). To see that \(Y\) is a principal bundle over \(S\) one uses the map \(\psi\) of (202) to check that \(S\) acts freely on \(Y\). The quotient of \(Y\) by the action of \(S\) is the quotient of \(X\) by the action of \(\hat{\mathbb{Z}}\). \((2)\) The fiber \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) has a canonical base point given by the idempotent \(u\in P_{p}({\mathbb{H}}_{\mathbb{Q}}),u^{2}=u\). Hence by applying Proposition 9.1, this fiber is canonically isomorphic to the quotient \(C_{\mathbb{Q}}/W_{p}\). By identifying \(C_{\mathbb{Q}}\) with \(\hat{\mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}\), this quotient coincides with the quotient of \(G_{p}\times{\mathbb{R}}_{+}^{*}\) by the powers of the element \((p,p)\in G_{p}\times{\mathbb{R}}_{+}^{*}\). Under the bijection \(\rho\mapsto-\log(\rho)\) from \((0,1)\) to \({\mathbb{R}}_{+}^{*}\), one obtains the same action as in (201) and hence the desired isomorphism. ∎ In order to obtain the analogue, for the global field \({\mathbb{K}}={\mathbb{Q}}\), of the fiber of the algebraic curve \(X^{\rm ab}\), we should apply the construction of Proposition 9.3 to a compact space \(X_{p}\) so that the following requirements are satisfied \((1)\)\(G_{p}\) acts freely and transitively on \(X_{p}\) \((2)\) The quotient of \(X_{p}\) by \(f_{p}^{\hat{\mathbb{Z}}}\) is canonically isomorphic to \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Proposition 8.14 provides a natural candidate for \(X_{p}\). Moreover, equation (187) shows that one can equivalently describe \(X_{p}\) as the space \({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\) and that the canonical identification of \(X_{p}/f_{p}^{\hat{\mathbb{Z}}}\) with \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) is given by the restriction map to the fixed points of \({\rm Fr}\) as in (188). We derive the definition of the following model for the fiber \(Y_{p}\) over a finite prime \(p\) \[Y_{p}=\left({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\times(0,1) \right)/\sigma^{\mathbb{Z}}.\] (205) ### Fiber over the archimedean place of \({\mathbb{Q}}\) We move now to the discussion of the analogues of the spaces \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\), \(X_{p}\) and \(Y_{p}\), when \(p\) is the archimedean prime \(p=\infty\) (_i.e._ the archimedean valuation). The space \({\rm Val}_{\infty}({{\mathbb{Q}}^{\rm cyc}})\) is the space of multiplicative norms on \({{\mathbb{Q}}^{\rm cyc}}\) whose restriction to \({\mathbb{Q}}\) is the usual absolute value. For \(v\in{\rm Val}_{\infty}({{\mathbb{Q}}^{\rm cyc}})\), the field completion \(({{\mathbb{Q}}^{\rm cyc}})_{v}\) is isomorphic to \({\mathbb{C}}\), thus one derives \[{\rm Val}_{\infty}({{\mathbb{Q}}^{\rm cyc}})={\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc }},{\mathbb{C}})/\{\pm 1\}\] (206) where \(\{\pm 1\}\subset\hat{\mathbb{Z}}^{*}={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{ \mathbb{Q}})\) corresponds to complex conjugation. It follows that for \(p=\infty\) the space \(X_{p}\) is simply \[X_{\infty}={\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc}},{\mathbb{C}}).\] (207) On the other hand, the fiber \(P_{\infty}({\mathbb{H}}_{\mathbb{Q}})\) is the quotient \(C_{\mathbb{Q}}/W_{\infty}\), where \(W_{\infty}={\mathbb{R}}^{*}\) is the cocompact subgroup of \(C_{\mathbb{Q}}\) given by classes of idèles, whose components are all \(1\) except at the archimedean place. Then, we derive that \[P_{\infty}({\mathbb{H}}_{\mathbb{Q}})=\hat{\mathbb{Z}}^{*}/\{\pm 1\}.\] (208) This discussion shows that at \(p=\infty\) there is no need for a mapping torus, and that the expected fiber is simply given by \[Y_{\infty}={\rm Val}_{\infty}({{\mathbb{Q}}^{\rm cyc}})={\mbox{Hom}}({{\mathbb {Q}}^{\rm cyc}},{\mathbb{C}})/\{\pm 1\}=X_{\infty}/\{\pm 1\}.\] (209) ### Ambient noncommutative space The model (205) for the fiber over a rational prime \(p\) is only a preliminary step toward the global construction of the “curve” which we expect to replace, when \({\mathbb{K}}={\mathbb{Q}}\), the geometric cover \(X^{\rm ab}\). In fact, one still needs to suitably combine these models into a noncommutative space to account for the presence of transversality factors in the explicit formulas. We explain why in some details below. In [11] we showed how to determine the counting function \(N(q)\) (a distribution on \([1,\infty)\)) which replaces, for \({\mathbb{K}}={\mathbb{Q}}\), the classical Weil counting function for a field \({\mathbb{K}}\) of functions of an algebraic curve \(Y\) over \({\mathbb{F}}_{p}\) (_cf._[27, 35]). The Weil counting function determines the number of rational points on the curve \(Y\) defined over field extensions \({\mathbb{F}}_{q}\) of \({\mathbb{F}}_{p}\) \[\#Y({\mathbb{F}}_{q})=N(q)=q-\sum_{\alpha}\alpha^{r}+1,\qquad q=p^{r}.\] The numbers \(\alpha\)’s are the complex roots of the characteristic polynomial of the Frobenius endomorphism acting on the étale cohomology \(H^{1}(Y\otimes\bar{\mathbb{F}}_{p},{\mathbb{Q}}_{\ell})\), for \(\ell\neq p\). In [11] we have shown that the distribution \(N(q)\) associated to the (complete) Riemann zeta function is described by the similar formula \[N(u)=u-\frac{d}{du}\left(\sum_{\rho\in Z}{\rm order}(\rho)\frac{u^{\rho+1}}{ \rho+1}\right)+1.\] (210) where \(Z\) is the set of non trivial zeros of the Riemann zeta function. This distribution is positive on \((1,\infty)\) and fulfills all the expected properties of a counting function. In particular, it takes the correct value \(N(1)=-\infty\) in agreement with the (expected) value of the Euler characteristic. In [14] we pushed these ideas further and we explained how to implement the trace formula understanding of the explicit formulas in number-theory, to express the distribution \(N(q)\) as an _intersection number_ involving the scaling action of the idèle class group on the adèle class space. This development involves a Lefschetz formula whose geometric side corresponds to the following expression of the counting distribution \(N(u)\) \[N(u)=\frac{d}{du}\varphi(u)+\kappa(u),\ \ \varphi(u)=\sum_{n<u}n\,\Lambda(n).\] (211) Here, \(\Lambda(n)\) is the von-Mangoldt function taking the value \(\log p\) at prime powers \(p^{\ell}\) and zero otherwise and \(\kappa(u)\) is the distribution defined, for any test function \(f\), as \[\int_{1}^{\infty}\kappa(u)f(u)d^{*}u=\int_{1}^{\infty}\frac{u^{2}f(u)-f(1)}{u^ {2}-1}d^{*}u+cf(1)\,,\qquad c=\frac{1}{2}(\log\pi+\gamma)\] (212) where \(\gamma=-\Gamma^{\prime}(1)\) is the Euler constant. The distribution \(\kappa(u)\) is positive on \((1,\infty)\) and in this domain it is equal to the function \(\kappa(u)=\frac{u^{2}}{u^{2}-1}\). The contribution in the counting distribution \(N(u)\) coming from the term \(\frac{d}{du}\varphi(u)\) in (211) can be understood geometrically as arising from a counting process performed on the fibers \(Y_{p}\) (each of them accounting for the delta functions located on the powers of \(p\)). The value \(\log(p)\) coming from the von-Mangoldt function \(\Lambda(n)\) corresponds to the length of the orbit in the mapping torus (_cf._[14], §2.2). On the other hand, as explained in [14], the contribution of the archimedean place cannot be understood in a naive manner as a simple counting process of points and its expression involves a transversality factor measuring the transversality of the action of the idèle class group with respect to periodic orbits. This shows that the periodic orbits cannot be considered in isolation and must be thought as (suitably) embedded in the ambient adèle class space. This development supplies a precious hint toward the final construction of the “curve” and shows that the role of ergodic theory and noncommutative geometry is indispensable. ### The BC-system over \({\mathbb{Z}}\) and \({\mathbb{F}}_{1^{\infty}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}\) Next, we shall explain how the BC-system over \({\mathbb{Z}}\) gives, for each \(p\), a natural embedding of the fiber \(Y_{p}\) (_cf._ (209)) into a noncommutative space constructed using the set \({\mathcal{E}}({\mathbb{C}}_{p})\) of the \({\mathbb{C}}_{p}\)-rational points of the affine group scheme \({\mathcal{E}}\) which describes the abelian part of the system (_cf._[15]). Since the fields \({\mathbb{C}}_{p}\) are abstractly pairwise isomorphic the obtained spaces are also abstractly isomorphic, but in a non canonical manner. In [15], following a proposal of C. Soulé for the meaning of the ring \({\mathbb{F}}_{1^{n}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}\), we noted that the inductive limit \[{\mathbb{F}}_{1^{\infty}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}:=\varinjlim_{n }{\mathbb{F}}_{1^{n}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}={\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}]\] (213) coincides with the abelian part of the algebra defining the integral BC-system. The description given in that paper of the BC-system as an affine pro-group scheme \({\mathcal{E}}\) over \({\mathbb{Z}}\) together with the dynamic of the action of a semigroup of endomorphisms, allows one to consider its rational points over any ring \(A\) \[{\mathcal{E}}(A)={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],A)\,.\] (214) Then, one can implement, for each rational prime \(p\), the canonical inclusion \[X_{p}={\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\subset{\mbox{Hom }}({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],{\mathbb{C}}_{p})={\mathcal{E}}({ \mathbb{C}}_{p})\,.\] (215) The next result shows that the space \[X({\mathbb{C}}_{p}):=\left({\mathcal{E}}({\mathbb{C}}_{p})\times(0,\infty) \right)/({\mathbb{N}}\times\{\pm 1\})\] (216) matches, for any \(p\) including \(p=\infty\), the definition of the adèle class space \({\mathbb{H}}_{\mathbb{Q}}\). The action of \(m=\pm n\) (in the semigroup \({\mathbb{N}}\times\{\pm 1\}\)) is the product of the linearization of the action \(e(\gamma)\mapsto e(m\gamma)\) on the (\({\mathbb{C}}_{p}\)-rational points of the) scheme \({\mathcal{E}}\), with the action on \((0,\infty)\) given by the map \(x\mapsto x^{m}\). **Proposition 9.4****.**: \((1)\) _The space \(X({\mathbb{C}})\) is canonically isomorphic to the adèle class space \({\mathbb{H}}_{\mathbb{Q}}\)._ \((2)\) _The subspace of the adèle class space made by classes whose archimedean component vanishes corresponds to the quotient_ \[{\mathcal{E}}({\mathbb{C}})/({\mathbb{N}}\times\{\pm 1\})=\hat{\mathbb{Z}}/({ \mathbb{N}}\times\{\pm 1\}).\] (217) Proof.: \((1)\) The space \({\mathcal{E}}({\mathbb{C}})\) is the space of complex characters of the abelian group \({\mathbb{Q}}/{\mathbb{Z}}\) and is canonically isomorphic to \(\hat{\mathbb{Z}}\). We use the map \(\rho\mapsto-\log(\rho)\) to map the interval \((0,\infty)\) to \({\mathbb{R}}\). Under this map the transformation \(x\mapsto x^{m}\) becomes the multiplication by \(m\). The action \(e(\gamma)\mapsto e(m\gamma)\) on the scheme \({\mathcal{E}}\) corresponds to the multiplication by \(m\) in \(\hat{\mathbb{Z}}\). Since any adèle class is equivalent to an element of \(\hat{\mathbb{Z}}\times{\mathbb{R}}\), (216) gives, for \(p=\infty\) \[X({\mathbb{C}})=\left(\hat{\mathbb{Z}}\times{\mathbb{R}}\right)/({\mathbb{N}} \times\{\pm 1\})={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}={\mathbb{H}}_{ \mathbb{Q}}.\] (218) \((2)\) follows from the identification (218).∎ Note that by using the inclusion \((0,1)\subset(0,\infty)\), one derives a natural inclusion \[Y_{p}=\left({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\times(0,1) \right)/\sigma^{\mathbb{Z}}\to\left({\mathcal{E}}({\mathbb{C}}_{p})\times(0, \infty)\right)/({\mathbb{N}}\times\{\pm 1\})=X({\mathbb{C}}_{p}).\] For \(p=\infty\) one has the natural inclusion \[Y_{\infty}={\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc}},{\mathbb{C}})/\{\pm 1\}\to \left({\mathcal{E}}({\mathbb{C}})\times(0,\infty)\right)/({\mathbb{N}}\times\{ \pm 1\})=X({\mathbb{C}})\] (219) which is obtained by using the canonical inclusion (215) for \(p=\infty\) and the fixed point \(1\in(0,\infty)\). The group ring \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) is a Hopf algebra for the coproduct \[\Delta(e(\gamma))=e(\gamma)\otimes e(\gamma)\,,\quad~{}\forall\gamma\in{ \mathbb{Q}}/{\mathbb{Z}}\] (220) and the antipode \(e(\gamma)\mapsto e(-\gamma)\), thus \({\mathcal{E}}\) is a group scheme. **Proposition 9.5****.**: _Let \(A\) be a commutative ring._ \((1)\) _The abelian group \({\mathcal{E}}(A)\) is torsion free._ \((2)\) _The space_ \[X(A)=\left({\mathcal{E}}(A)\times(0,\infty)\right)/({\mathbb{N}}\times\{\pm 1\})\] (221) _is a module over the hyperring \({\mathbb{H}}_{\mathbb{Q}}\)._ \((3)\) _For any rational prime \(p\), \(X({\mathbb{C}}_{p})\) is a free module of rank one over \({\mathbb{H}}_{\mathbb{Q}}\)._ Proof.: \((1)\) One has \[{\mathcal{E}}(A)={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],A)={ \mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},A^{\times})\] where the second Hom is taken in the category of abelian groups. Since the group \({\mathbb{Q}}/{\mathbb{Z}}\) is divisible the group \({\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},H)\) has no torsion, for any abelian group \(H\). \((2)\) We first show that \(X(A)\) is a hypergroup and in fact a vector space over the Krasner hyperfield \(\mathbf{K}=\{0,1\}\) (_cf._[13]). The two abelian groups \({\mathcal{E}}(A)\) and \((0,\infty)\) are both torsion free, thus one gets \[\left({\mathcal{E}}(A)\times(0,\infty)\right)/({\mathbb{N}}\times\{\pm 1\})= \left(\left({\mathcal{E}}(A)\times(0,\infty)\right)\otimes_{\mathbb{Z}}{ \mathbb{Q}}\right)/{\mathbb{Q}}^{\times}\] (222) which is a projective space, hence a vector space over \(\mathbf{K}\) (_cf._[13]). Next we show that \(X(A)\) is a module over \({\mathbb{H}}_{\mathbb{Q}}\). We use the canonical ring isomorphism \(\hat{\mathbb{Z}}={\mbox{End}}_{\mathbb{Z}}({\mathbb{Q}}/{\mathbb{Z}})\) to define the following ring homomorphism from \(\hat{\mathbb{Z}}\) to the ring \({\mbox{End}}_{\mathbb{Z}}({\mathcal{E}}(A))\) \[c_{A}:\hat{\mathbb{Z}}\to{\mbox{End}}_{\mathbb{Z}}({\mathcal{E}}(A))\,,\ \ c_{ A}(\alpha)\xi=\xi\circ\alpha\,,\quad~{}\forall\xi\in{\mbox{Hom}}({\mathbb{Q}}/ {\mathbb{Z}},A^{\times}).\] (223) The map \[p:{\mathbb{R}}\to{\mbox{End}}_{\mathbb{Z}}({\mathbb{R}}_{+}^{*}),\quad p( \lambda)x=x^{\lambda}\] (224) is a ring homomorphism, thus \(c_{A}\times p\) defines a ring homomorphism from \(\hat{\mathbb{Z}}\times{\mathbb{R}}\) to the endomorphisms of the abelian group \({\mathcal{E}}(A)\times(0,\infty)\). For any \(m\in{\mathbb{Z}}\subset\hat{\mathbb{Z}}\times{\mathbb{R}}\), one has \[(c_{A}\times p)(m)((e(\gamma),x))=(e(m\gamma),x^{m}),\] (225) thus the restriction of \(c_{A}\times p\) to the monoid of non-zero elements of \({\mathbb{Z}}\) gives the equivalence relation which defines \(X(A)\) as in (221). It follows an action of the hyperring \[\left((\hat{\mathbb{Z}}\times{\mathbb{R}})\otimes_{\mathbb{Z}}{\mathbb{Q}} \right)/{\mathbb{Q}}^{\times}={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{\times}= {\mathbb{H}}_{\mathbb{Q}}\] on the hypergroup (222). \((3)\) It is easy to see that, once one fixes an embedding \(\rho:{{\mathbb{Q}}^{\rm cyc}}\to{\mathbb{C}}_{p}\) and an \(x\in(0,\infty)\) and a real number \(x\neq 1\), the element \((\rho,x)\in X({\mathbb{C}}_{p})\) is a generator of \(X({\mathbb{C}}_{p})\) as a free module over \({\mathbb{H}}_{\mathbb{Q}}\). ∎ The next result displays some interesting arithmetic-geometric properties of the scheme \({\mathcal{E}}\). **Proposition 9.6****.**: \((1)\) _Let \({\mathbb{Q}}_{p}^{\rm ab}\subset{\mathbb{C}}_{p}\) be the maximal abelian extension of \({\mathbb{Q}}_{p}\). Then the natural map \({\mathcal{E}}({\mathbb{Q}}_{p}^{\rm ab})\to{\mathcal{E}}({\mathbb{C}}_{p})\) is a bijection of sets._ \((2)\) _Let \({\mathbb{Q}}_{p}^{\rm ur}\subset{\mathbb{Q}}_{p}^{\rm ab}\) be the maximal unramified extension of \({\mathbb{Q}}_{p}\) and \({\mathbb{Z}}_{p}^{\rm ur}\subset{\mathbb{Q}}_{p}^{\rm ur}\) the valuation ring of the \(p\)-adic valuation. Then the natural map \({\mathcal{E}}({\mathbb{Z}}_{p}^{\rm ur})\to{\mathcal{E}}({\mathbb{Q}}_{p}^{\rm ur})\) is a bijection of sets._ \((3)\) _Let \(\epsilon:{\mathbb{Z}}_{p}^{\rm ur}\to\bar{\mathbb{F}}_{p}\) be the residue homomorphism. Then the associated map \({\mathcal{E}}({\mathbb{Z}}_{p}^{\rm ur})\to{\mathcal{E}}(\bar{\mathbb{F}}_{p})\) is a bijection._ \((4)\) _The \({\mathbb{H}}_{\mathbb{Q}}\)-module_ \[X(\bar{\mathbb{F}}_{p})\simeq X({\mathbb{Z}}_{p}^{\rm ur})\simeq X({\mathbb{Q} }_{p}^{\rm ur})\subset X({\mathbb{Q}}_{p}^{\rm ab})\simeq X({\mathbb{C}}_{p})\] _is described as_ \[X(\bar{\mathbb{F}}_{p})=\mathfrak{p}_{p}X({\mathbb{C}}_{p})\] (226) _where \(\mathfrak{p}_{p}\in{\rm Spec}\,({\mathbb{H}}_{\mathbb{Q}})\) is the prime ideal of adèle classes whose \(p\)-component vanishes._ Proof.: \((1)\) Let \(\rho\in{\mathcal{E}}({\mathbb{C}}_{p})={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/ {\mathbb{Z}}],{\mathbb{C}}_{p})\). Then the image of \(\rho\) is contained in the subfield of \({\mathbb{C}}_{p}\) generated over \({\mathbb{Q}}\) by roots of unity, which is contained in \({\mathbb{Q}}_{p}^{\rm ab}\). \((2)\) Let \(\rho\in{\mathcal{E}}({\mathbb{Q}}_{p}^{\rm ur})={\mbox{Hom}}({\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],{\mathbb{Q}}_{p}^{\rm ur})\). Then the image of \(\rho\) is contained in the subring of \({\mathbb{Q}}_{p}^{\rm ur}\) generated over \({\mathbb{Z}}\) by roots of unity (of order prime to \(p\)) which is contained in \({\mathbb{Z}}_{p}^{\rm ur}\). \((3)\) Let \(\rho\in{\mathcal{E}}({\mathbb{Z}}_{p}^{\rm ur})={\mbox{Hom}}({\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],{\mathbb{Z}}_{p}^{\rm ur})\). Then \(\rho\) is entirely characterized by the group homomorphism \[\rho:{\mathbb{Q}}/{\mathbb{Z}}\to G\] where \(G\) is the group of roots of unity in \({\mathbb{Z}}_{p}^{\rm ur}\), which is non canonically isomorphic to the group \(\mu^{(p)}\) of abstract roots of unity of order prime to \(p\). Similarly an element of \({\mathcal{E}}(\bar{\mathbb{F}}_{p})={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/{ \mathbb{Z}}],\bar{\mathbb{F}}_{p})\) is entirely characterized by the associated group homomorphism from \({\mathbb{Q}}/{\mathbb{Z}}\) to \(\bar{\mathbb{F}}_{p}^{*}\). Since the residue morphism \(\epsilon\) gives an isomorphism \(G\stackrel{{\simeq}}{{\to}}\bar{\mathbb{F}}_{p}^{*}\) one obtains the conclusion. \((4)\) One has \(\hat{\mathbb{Z}}={\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},{\mathbb{Q}}/{\mathbb{ Z}})\). Let, as above, \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{\mathbb{Z}}\) be the subgroup of elements of denominator prime to \(p\). Then the subset \({\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}) \subset{\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},{\mathbb{Q}}/{\mathbb{Z}})\) is given by \[\{(a_{\ell})\in\prod{\mathbb{Z}}_{\ell}=\hat{\mathbb{Z}}\mid\ \ a_{p}=0\}\] which corresponds to the prime, principal ideal \(\mathfrak{p}_{p}\) of the hyperring structure \({\mathbb{H}}_{\mathbb{Q}}\) inherent to the adèle class space (_cf._[13]).∎ ## 10. The standard model of \(\bar{\mathbb{F}}_{p}\) and the BC-system As shown in section 8, the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) is intimately related to the space of sequences of irreducible polynomials \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), fulfilling the basic conditions of the Conway polynomials (_cf._ Theorem 8.7) and hence to the explicit construction of an algebraic closure of \({\mathbb{F}}_{p}\). The normalization condition using the lexicographic ordering just specifies a particular element \(v_{c}\) of \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Since the explicit computation of the sequence \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), associated to \(v_{c}\) has been proven to be completely untractable, B. de Smit and H. Lenstra have recently devised a more efficient construction of \(\bar{\mathbb{F}}_{p}\) (_cf._[18]). Our goal in this section is to make explicit the relation between their construction, the BC-system and the sought for “curve”. When \({\mathbb{K}}\) is a global field of positive characteristic _i.e._ the function field of an algebraic curve over a finite field \({\mathbb{F}}_{q}\), the intermediate extension \({\mathbb{K}}\subset\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}} \subset{\mathbb{K}}^{\rm ab}\) plays an important geometric role since it corresponds to working over an algebraically closed field. For \({\mathbb{K}}={\mathbb{Q}}\), it is therefore natural to ask for an intermediate extension \({\mathbb{Q}}\subset L\subset{{\mathbb{Q}}^{\rm cyc}}\) playing a similar role. One feature of the former extension is that the residue fields are algebraically closed. In their construction, de Smit and Lenstra use the intermediate extension \({\mathbb{Q}}\subset{{\mathbb{Q}}^{\rm cycl}_{\Delta}}\subset{{\mathbb{Q}}^{\rm cyc}}\) which comes very close to fulfill the expected properties. For each prime \(\ell\), let us denote by \(\Delta_{\ell}\subset{\mathbb{Z}}_{\ell}^{*}\) the torsion subgroup. For \(\ell=2\) one has \(\Delta_{2}=\{\pm 1\}\), while for \(\ell\neq 2\) one gets \(\Delta_{\ell}=\tau({\mathbb{F}}_{\ell}^{*})\), where \(\tau:{\mathbb{F}}_{\ell}\to{\mathbb{Z}}_{\ell}\) is the Teichmüller lift. The product \[\Delta:=\prod_{\ell}\Delta_{\ell}\subset\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}\] (227) is a compact group, and a subgroup of the Galois group \(\hat{\mathbb{Z}}^{*}={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\). By Galois theory, one can thus associate to \(\Delta\) a (fixed) field extension \[L={{\mathbb{Q}}^{\rm cycl}_{\Delta}}\subset{{\mathbb{Q}}^{\rm cyc}}.\] (228) Notice that one derives a subsystem of the BC-system given by the fixed points of the action of \(\Delta\). At the rational level and by implementing the cyclotomic ideal \(J\) of Definition 8.1, one obtains the exact sequence of algebras \[0\to J\cap{{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\to{{\mathbb{Q}}[{ \mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\stackrel{{ q}}{{\to}}{{\mathbb {Q}}^{\rm cycl}_{\Delta}}\to 0\] (229) The image of the restriction to \({{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\) of the homomorphism \(q\) is contained in the integers of \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\) and one has \[{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\simeq\hat{\mathbb{Z }}^{*}/\Delta\simeq\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}.\] (230) The space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) is the total space of a principal bundle whose base is the space \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) of valuations on \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\) extending the \(p\)-adic valuation. The group of the principal bundle is the quotient of \(\Delta\) by its intersection \(\Delta_{p}\) with the isotropy group of elements of \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). The projection \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\to{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl }_{\Delta}})\) is given by restriction of valuations from \({{\mathbb{Q}}^{\rm cyc}}\) to \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\). For \(w\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\), the isotropy group \(\Pi_{p}\) of \(w\) for the action of \({\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\) is the image of the isotropy group of \(v\) in \({\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\) for any extension \(v\) of \(w\) to \({{\mathbb{Q}}^{\rm cyc}}\). It follows from Lemma 8.2 that the isotropy subgroup of \(v\) is \({\mathbb{Z}}_{p}^{*}\times f_{p}^{\hat{\mathbb{Z}}}\subset{\mathbb{Z}}_{p}^{*} \times G_{p}\), thus one gets \[\Pi_{p}\simeq{\mathbb{Z}}_{p}^{*}/\Delta_{p}\times\overline{f_{p}^{\mathbb{Z}} }\,,\ \ \overline{f_{p}^{\mathbb{Z}}}\subset\prod_{\ell\neq p}{\mathbb{Z}}_{ \ell}^{*}/\Delta_{\ell}.\] (231) **Lemma 10.1****.**: _For each prime \(\ell\) the group \({\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\) is canonically isomorphic to the additive group \({\mathbb{Z}}_{\ell}\). Moreover, for each prime \(p\neq\ell\) the closed subgroup of \({\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\) generated by \(p\) is open and of finite index \(\ell^{u(p,\ell)}\) where_ \[u(p,\ell)=\begin{cases}v_{\ell}(p^{\ell-1}-1)-1,&\text{for $\ell>2$}\\ v_{2}(p^{2}-1)-3,&\text{for $\ell=2$.}\end{cases}\] (232) Proof.: For each prime \(\ell\) there is a canonical isomorphism of groups \[{\mathbb{Z}}_{\ell}^{*}\stackrel{{\sim}}{{\to}}\Delta_{\ell}\times {\mathbb{Z}}_{\ell},\quad x\mapsto(\omega(x),i_{\ell}(x))\] (233) where the group \({\mathbb{Z}}_{\ell}\) is viewed as an additive group. For \(\ell\) odd, \(\omega(x)\) is the unique \(\ell-1\) root of unity which is congruent to \(x\) modulo \(\ell\) and \(i_{\ell}(x)\), as in (145), is the ratio \({\log_{\ell}x/\log_{\ell}(1+\ell)}\). For \(\ell=2\), \(\omega(x)=\pm 1\) is congruent to \(x\) modulo \(4\) and \(i_{2}(x)=\log_{2}x/\log_{2}(1+4)\). The first statement thus follows. The second statement follows since one has \[v_{\ell}(i_{\ell}(p))=u(p,\ell)\] and the closed subgroup of \({\mathbb{Z}}_{\ell}\) generated by \(i_{\ell}(p)\) is \(\ell^{u(p,\ell)}{\mathbb{Z}}_{\ell}\).∎ Under the isomorphisms \[{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\simeq\prod_{\ell}{ \mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\simeq\prod_{\ell}{\mathbb{Z}}_{\ell} \simeq\hat{\mathbb{Z}}\] (234) one gets, by the Chinese remainder theorem, that \[\Pi_{p}\simeq{\mathbb{Z}}_{p}\times\prod_{\ell\neq p}\ell^{u(p,\ell)}{\mathbb{ Z}}_{\ell}\subset\hat{\mathbb{Z}}\,.\] (235) Notice the independence of the places \(\ell\) in the above formula which makes the group \(\Pi_{p}\) a cartesian product and allows one to express \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) as an infinite product of finite sets. To label concretely these finite sets consider, for each prime \(\ell\) the \({\mathbb{Z}}_{\ell}\)-extension \({\mathbb{B}}_{\infty}(\ell)\) of \({\mathbb{Q}}\). One has \({\mathbb{B}}_{\infty}(\ell)=\cup_{k}{\mathbb{B}}_{k}(\ell))\) where, for \(k\in{\mathbb{N}}\), the finite extension \({\mathbb{B}}_{k}(\ell)\) of \({\mathbb{Q}}\) is associated to \(\ell^{-k}\in{\mathbb{Q}}/{\mathbb{Z}}\) viewed as a character of \(\hat{\mathbb{Z}}\simeq{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\). For \(\ell\) odd, \({\mathbb{B}}_{k}(\ell)\) is the fixed subfield for the action of \(\Delta_{\ell}\) on the extension of \({\mathbb{Q}}\) generated by a primitive root of unity of order \(\ell^{k+1}\). For \(\ell=2\) one uses a primitive root of unity of order \(2^{k+2}\). We denote by \({\mathbb{B}}(\ell,p)={\mathbb{B}}_{u(p,\ell)}(\ell)\): this is a cyclic extension of \({\mathbb{Q}}\) of degree \(\ell^{u(p,\ell)}\). The Artin reciprocity law shows that, for \(p\) a prime \(p\neq\ell\), the reduction modulo \(p\) of the integers of \({\mathbb{B}}(\ell,p)\), decomposes as a product of \(\ell^{u(p,\ell)}\) copies of \({\mathbb{F}}_{p}\), parameterized by the set \({\rm Val}_{p}({\mathbb{B}}(\ell,p))\) of extensions of the \(p\)-adic valuation to \({\mathbb{B}}(\ell,p)\), which is a finite set of cardinality \(\ell^{u(p,\ell)}\). The following result is a consequence of the construction of the “standard model” of de Smit and Lenstra for the algebraic closure of a finite field **Theorem 10.2****.**: _Let \(p\) be a rational prime._ \((1)\) _For \(\ell\neq p\) a prime, the restriction map \({\rm Val}_{p}({\mathbb{B}}_{\infty}(\ell))\to{\rm Val}_{p}({\mathbb{B}}(\ell,p))\) is bijective._ \((2)\) _The restriction maps from \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\) to \({\mathbb{B}}_{\infty}(\ell)\) give a bijection_ \[{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})=\prod_{\ell\neq p}{\rm Val}_ {p}({\mathbb{B}}_{\infty}(\ell)).\] (236) \((3)\) _The restriction of \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) to \({\mathbb{Q}}^{\rm cyc,p}_{\Delta}\) is unramified and the residue field is isomorphic to_ \[\bigcup_{n\in I(p)}{\mathbb{F}}_{p^{n}}\subset\bar{\mathbb{F}}_{p}\] (237) _where \(I(p)\subset{\mathbb{N}}\) denotes the subset of positive integers which are prime to \(p\)._ Proof.: \((1)\) It is enough to show that the image of the isotropy group \({\mathbb{Z}}_{p}^{*}\times p^{\hat{\mathbb{Z}}}\subset{\mathbb{Z}}_{p}^{*} \times G_{p}\) of Lemma 8.2, maps surjectively onto the Galois group \({\rm Gal}({\mathbb{B}}_{\infty}(\ell):{\mathbb{B}}(\ell,p))\). This follows from Lemma 10.1. \((2)\) The restriction maps determine an equivariant map \[{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\to\prod_{\ell\neq p}{\rm Val }_{p}({\mathbb{B}}_{\infty}(\ell))\] (238) for the action of the Galois group \({\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\). By (234) and (235), the isotropy groups are the same so that the map (238) is bijective. \((3)\) By extending \(v\) to an element of \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) one gets that the restriction to \({\mathbb{Q}}^{\rm cyc,p}\) and hence to \({\mathbb{Q}}^{\rm cyc,p}_{\Delta}\) is unramified. Moreover the residue field is determined by the topology on the closure set of the action of the Frobenius, _i.e._ on \(\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}\). The result follows.∎ Next, we shall explain the link with the notations used by de Smit and Lenstra and their construction. First, we recall that the additive group \({\mathbb{Q}}/{\mathbb{Z}}\) is the direct sum of its \(\ell\)-torsion components \[H_{\ell}=\{\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\mid\exists n\ \ell^{n}\alpha=0\} \simeq{\mathbb{Q}}_{\ell}/{\mathbb{Z}}_{\ell}.\] (239) Thus the group ring \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) can be written as a tensor product \[{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]=\bigotimes_{\ell\,\rm prime}{\mathbb{Z }}[H_{\ell}].\] (240) The natural action of \(\hat{\mathbb{Z}}^{*}\) on \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) by automorphisms of the group \({\mathbb{Q}}/{\mathbb{Z}}\) factorizes in the individual actions of \({\mathbb{Z}}_{\ell}^{*}={\rm Aut}(H_{\ell})\). One lets \(A_{\ell}\) be the ring \({\mathbb{Z}}[X_{0},X_{1},\ldots]\) modulo the ideal generated by \[\sum_{j=0}^{\ell-1}X_{0}^{j}\,,\ \ X_{k+1}^{\ell}-X_{k}\,,\quad~{}\forall k \geq 0.\] (241) Thus one has \(X_{0}^{\ell}=1\) in \(A_{\ell}\) and \(X_{k+1}^{\ell}=X_{k}\) for all \(k\geq 0\). The algebra \(B_{\ell}\) of de Smit and Lenstra is defined as \(B_{\ell}=A_{\ell}^{\Delta_{\ell}}\). The next lemma shows that the algebra \(B_{\ell}\) is intimately related to the fixed point algebra \({\mathbb{Z}}[H_{\ell}]^{\Delta_{\ell}}\). **Lemma 10.3****.**: _One has_ \[B_{\ell}\simeq({\mathbb{Z}}[H_{\ell}]/J)^{\Delta_{\ell}}\] (242) _where \(J\) is the ideal generated by the relations \(\sum_{\ell\gamma=0}e(\gamma)\in{\mathbb{Z}}[H_{\ell}]\)._ Proof.: It follows from the relations (241) that \(X_{k}^{\ell^{k+1}}=1\) for all \(k\). Moreover, the map \(\theta(e(\ell^{-k}))=X_{k-1}\) extends to a surjective homomorphism \({\mathbb{Z}}[H_{\ell}]\to A_{\ell}\) with kernel \(J\), one thus gets (242).∎ One has the trace map \[\Sigma:A_{\ell}\to B_{\ell},\qquad\Sigma(x)=\sum_{\sigma\in\Delta_{\ell}} \sigma(x)\] (243) and natural ring homomorphisms \(B_{\ell}\to E(\ell)\). De Smit and Lenstra (_cf._[18]) lift the natural generator of \(E_{k}(\ell)\) as an extension of \(E_{k-1}(\ell)\), and the Galois conjugates under \({\rm Gal}(E_{k}(\ell):E_{k-1}(\ell))\) as the following elements of \(B_{\ell}\) \[\eta_{\ell,k,i}=\Sigma(e(\frac{1}{\ell^{k+1}}+\frac{i}{\ell})),\ \ i=0,\ldots \ell-1.\] (244) When \(\ell=2\), one has simply \({\Delta_{2}}=\{\pm 1\}\subset{\mathbb{Z}}_{2}^{*}\) and in this case the above list of elements reduces to \[\eta_{2,k}=\Sigma(e(\frac{1}{2^{k+2}})).\] (245) The two authors show that the prime ideals \(\mathfrak{p}\) of \(B_{\ell}\) which contain \(p\), are uniquely specified by a finite system of elements \(a(\mathfrak{p},j)\in{\mathbb{F}}_{p}\), \(0\leq j<\ell u(p,\ell)\). More precisely, \(\mathfrak{p}\) is generated by \(p\) and by the \(\eta_{\ell,k+1,i}-a(\mathfrak{p},i+k\ell)\) for \(0\leq k<u(p,\ell)\) and \(0\leq i<\ell\). To complete the dictionary with the notations of de Smit and Lenstra, we leave to the reader as an exercise to show that \(\bullet\) The prime ideals \(\mathfrak{p}\) of \(B_{\ell}\) which contain \(p\) correspond to the valuations \({\rm Val}_{p}({\mathbb{B}}_{\infty}(\ell))\). \(\bullet\) The subfield \({\mathbb{Q}}_{p}\cap{\mathbb{B}}_{\infty}(\ell)\subset{\mathbb{B}}_{\infty}( \ell)_{v}\) is equal to \({\mathbb{B}}(\ell,p)\). \(\bullet\) The system of elements \(a(\mathfrak{p},j)\in{\mathbb{F}}_{p}\) corresponds, as in Proposition 8.13, to the residue of the inclusion \(\gamma_{v}:{\mathbb{B}}(\ell,p)\to{\mathbb{Q}}_{p}\), defined as in Proposition 8.12. Theorem 10.2 does not yield the full algebraic closure of \({\mathbb{F}}_{p}\) but only the subfield \[\bigcup_{n\in I(p)}{\mathbb{F}}_{p^{n}}\subset\bar{\mathbb{F}}_{p}.\] (246) Thus it remains to understand how to produce naturally the missing part \[\bigcup_{n}{\mathbb{F}}_{p^{p^{n}}}\subset\bar{\mathbb{F}}_{p}\] (247) in such a way that the tensor product over \({\mathbb{F}}_{p}\) yields \(\bar{\mathbb{F}}_{p}\). De Smit and Lenstra construction of \({\mathbb{F}}_{p^{p^{\infty}}}=\varinjlim_{n}{\mathbb{F}}_{p^{p^{n}}}\) is performed using the following Artin–Schreier equations \[y_{0}^{p}-y_{0}=1\,,\ \ y_{n+1}^{p}-y_{n+1}+\frac{y_{n}}{y_{n}+1}=0\,,\quad~{} \forall n\geq 0\] (248) which have the advantage of simplicity. E. Witt gave in [38] a conceptual construction of \({\mathbb{F}}_{p^{p^{\infty}}}\) based on the Witt functor \({\mathbb{W}}_{p^{\infty}}\) and its finite truncations \({\mathbb{W}}_{p^{n}}\). The addition of two Witt vectors \(x=(x_{j})\) and \(y=(y_{j})\) is a vector whose components \(S_{j}(x,y)\) were proven by Witt to be polynomials with integer coefficients. Note also that for \(p\neq 2\) the Witt components of \(-x\) (the additive inverse of \(x\)) are simply \(-x_{j}\), but this result does not hold for \(p=2\). Recall also that in terms of the Witt vectors, the Frobenius \(F\) is given in characteristic \(p\), by \((F(x))_{j}=x_{j}^{p}\,,\quad~{}\forall j\). From [38], one derives the following result **Theorem 10.4****.**: _Let \(n\in{\mathbb{N}}\). Let \(R_{n}={\mathbb{F}}_{p}[x_{0},x_{1},\ldots,x_{n-1}]\) be the ring of polynomials in \(n\) variables and \(J_{n}\subset R_{n}\) the ideal generated by the components of the Witt vector \(F(x)-x-1\), where \(x\in{\mathbb{W}}_{p^{n-1}}(R)\) is the Witt vector with components \(x_{j}\). Then \(J_{n}\) is a prime ideal and the quotient field of the integral ring \(R_{n}/J_{n}\) defines the field extension \(E_{n}\simeq{\mathbb{F}}_{p^{p^{n}}}\)._ _As an extension of \(E_{n-1}\), \(E_{n}\) is given by an Artin–Schreier equation of the form_ \[X^{p}=X+\alpha,\ \ \alpha\in E_{n-1}.\] (249) One derives, for instance, that the first extensions for \(p=2\) are given by the equations with coefficients in \({\mathbb{F}}_{2}\) \[x_{0}^{2} = 1+x_{0}\] \[x_{1}^{2} = x_{0}+x_{1}\] \[x_{2}^{2} = x_{0}+x_{0}^{3}+x_{0}x_{1}+x_{2}\] \[x_{3}^{2} = x_{0}+x_{0}^{3}+x_{0}^{5}+x_{0}^{7}+x_{0}^{2}x_{1}+x_{0}^{3}x_{1 }+x_{0}^{4}x_{1}+x_{0}x_{1}^{3}+x_{0}x_{2}+x_{0}^{3}x_{2}+x_{0}x_{1}x_{2}+x_{3}\] For \(p=3\) one gets the following equations with coefficients in \({\mathbb{F}}_{3}\) \[x_{0}^{3} = 1+x_{0}\] \[x_{1}^{3} = 2x_{0}+2x_{0}^{2}+x_{1}\] \[x_{2}^{3} = 2x_{0}+2x_{0}^{2}+2x_{0}^{4}+2x_{0}^{5}+2x_{0}^{7}+2x_{0}^{8}+2x _{0}^{2}x_{1}+x_{0}^{3}x_{1}+2x_{0}^{4}x_{1}+x_{0}x_{1}^{2}+x_{0}^{2}x_{1}^{2} +x_{2}\] In this way one obtains a completely canonical construction of the field \({\mathbb{F}}_{p^{p^{\infty}}}\) by simply writing the equation \(F(X)=X+1\) in the ring of Witt vectors \({\mathbb{W}}_{p^{\infty}}\). ## References * [1] G. Almkvist, _Endomorphisms of finitely generated projective modules over a commutative ring_, Arkiv för Matematik Volume 11, Numbers 1-2 (1973), 263–301. * [2] G. Almkvist, _The Grothendieck ring of the category of endomorphisms_, J. of Algebra 28,(1974), 375–388. * [3] R. Auer, _A functorial property of nested Witt vectors_, J. of Algebra 252 (2002), 293–299. * [4] J.B. Bost, A. Connes, _Hecke algebras, type III factors and phase transitions with spontaneous symmetry breaking in number theory_, Selecta Math. (N.S.) 1 (1995), no. 3, 411–457. * [5] N. Bourbaki _Algebra II. Chapters 4–7_. Translated from the 1981 French edition by P. M. Cohn and J. Howie. Reprint of the 1990 English edition. Elements of Mathematics (Berlin). Springer-Verlag, Berlin, 2003. * [6] P. Cartier, _Groupes formels associés aux vecteurs de Witt généralisés_, Compt. Rend. Acad. Sci. Paris, Ser. A-B 265 (1967), A49–A52. * [7] A. Connes, _Trace formula in noncommutative geometry and the zeros of the Riemann zeta function_, Selecta Math. (N.S.) 5 (1999), no. 1, 29–106. * [8] A. Connes _The Witt construction in characteristic one and quantization_, to appear in the Proceedings volume dedicated to H. Moscovici (2011). * [9] A. Connes _The BC-system and L-functions_, to appear in Japanese Journal of Mathematics. * [10] A. Connes, C. Consani _On the notion of geometry over \({\mathbb{F}}_{1}\)_, to appear in Journal of Algebraic Geometry; arXiv08092926v2 [mathAG]. * [11] A. Connes, C. Consani _Schemes over \({\mathbb{F}}_{1}\) and zeta functions_, Compositio Mathematica 146 (6), (2010) 1383–1415; doi:10.1112/S0010437X09004692. * [12] A. Connes, C. Consani _Characteristic \(1\), entropy and the absolute point_, in Proceedings of the 21st JAMI Conference “Noncommutative Geometry, arithmetic and related topics”, Baltimore 2009, JHUP (2011); (in press). arXiv:0911.3537v1 [mathAG]. * [13] A. Connes, C. Consani _The hyperring of adèle classes_, Journal iof Number Theory 131 (2011) 159–194. * [14] A. Connes, C. Consani _From monoids to hyperstructures: in search of an absolute arithmetic_, in Casimir Force, Casimir Operators and the Riemann Hypothesis, de Gruyter (2010), 147–198. * [15] A. Connes, C. Consani, M. Marcolli, _Fun with \({\mathbb{F}}_{1}\)_, Journal of Number Theory 129 (2009) 1532–1561. * [16] A. Connes, M. Marcolli, _Noncommutative Geometry, Quantum Fields, and Motives_, Colloquium Publications, Vol.55, American Mathematical Society, 2008. * [17] C. Consani, M. Marcolli, _Quantum statistical mechanics over function fields_. J. Number Theory 123 (2007), no. 2, 487–528. * [18] B. de Smit, H. W. Lenstra _Standard model for finite fields: the definition_, http://www.math.leidenuniv.nl/ desmit/papers/standard-models.pdf * [19] D. Grayson _Grothendieck rings and Witt vectors_, Comm. Algebra 6 (1978), no. 3, 249–255. * [20] A. Grothendieck _La théorie des classes de Chern_. (French) Bull. Soc. Math. France 86 1958 137–154. * [21] R. Hartshorne _Algebraic Geometry_, Graduate Texts in Mathematics 52, Springer-Verlag, New York Heidelberg Berlin 1977. * [22] M. Hazewinkel _Witt vectors. Part 1_, in: M. Hazewinkel, ed., Handbook of algebra. Volume 6, Elsevier, 2009, 319–472. * [23] M. Hazewinkel _Operations in the \(K\)-theory of endomorphisms_, J. of Algebra 84 (1983), 285–304. * [24] L. Hesselholt _The big De Rham Witt complex_, arXiv:1006.3125. * [25] Kelley-Spanier _Euler characteristics_ Pacific Journal of Mathematics 26, 2 (1968). * [26] H. W. Lenstra, _Finding isomorphisms between finite fields_, Math. Comp. 56 (1991), no. 193, 329–347 * [27] Y. I. Manin, _Lectures on zeta functions and motives (according to Deninger and Kurokawa)_ Columbia University Number-Theory Seminar (1992), Astérisque No. 228 (1995), 4, 121–163. * [28] D. Mumford, _Lectures on Curves on an Algebraic Surface_, Annals of Mathematics Studies, 59, Princeton, NJ: Princeton University Press. * [29] D. Quillen _On the Cohomology and K-Theory of the General Linear Groups Over a Finite Field_ Annals of Mathematics, 2nd Ser., Vol. 96, No. 3. (1972), pp. 552-586. * [30] J. Rabinoff, _The theory of Witt vectors_. Notes available at http://math.harvard.edu/ rabinoff/misc/witt.pdf * [31]J. P. Ramis, _Séries divergentes et théories asymptotiques_. Bull. Soc. Math. France 121 (1993), Panoramas et Synthèses, suppl., 74 pp. * [32] A. Robert, _A course in \(p\)-adic analysis_. (English summary) Graduate Texts in Mathematics, 198. Springer-Verlag, New York, 2000. * [33] L. Roberts, _The ring of Witt vectors_, in Queen’s Papers in Pure and Appl. Math. 105 (1997) 2–36. * [34] J. P. Serre, _Corps locaux_. (French) Deuxième edition. Publications de l’Université de Nancago, No. VIII. Hermann, Paris, 1968. * [35] C. Soulé, _Les variétés sur le corps à un élément_. Mosc. Math. J. 4 (2004), no. 1, 217–244. * [36] O. Teichmüller, _Über die Struktur diskret bewerteter perfekter Körper_, Nachr. Ges. Wiss. Göttingen N.F. 1 (1936), 151-161. * [37] L. Washington, _Introduction to cyclotomic fields_. Second edition. Graduate Texts in Mathematics, 83. Springer-Verlag, New York, 1997. * [38] E. Witt, _Zyklische Körper und Algebren der Charakteristik \(p\) vom Grad \(p^{n}\). Struktur diskret bewerteter perfekter Körper mit vollkommenem Restklassen-körper der Charakteristik \(p\)_. J. Reine Angew. Math. , 176 (1937), 126–140. * [39] E. Witt, _Vektorkalkül und Endomorphismen der Einspotenzreihengruppe_ in: I. Kersten (Ed.), Ernst Witt, Collected Papers, Springer, Berlin, 1998, 157–164.

# Об арифметике BC-системы BC-система является одной из основных систем счисления, используемых для арифметических операций. Основное свойство BC-системы заключается в том, что она позволяет представлять числа с использованием ограниченного набора символов. Основной идеей BC-системы является использование символов 'B' и 'C' для представления чисел. Каждый символ имеет свою числовую эквивалентность, определяющую его значение в системе счисления. Например: - Символ 'B' имеет числовую эквивалентность 0. - Символ 'C' имеет числовую эквивалентность 1. Таким образом, число 'BCB' в BC-системе будет представлять собой число, эквивалентное 1010 в двоичной системе счисления. Операции сложения и вычитания в BC-системе выполняются путем простого объединения или разделения символов 'B' и 'C'. Например: - Сложение: 'BCB' + 'C' = 'BCC' (1010 + 1 = 1011) - Вычитание: 'BCC' - 'C' = 'BCB' (1011 - 1 = 1010) BC-система также позволяет выполнять умножение и деление с использованием тех же основных операций сложения и вычитания. Это делается путем повторных применений этих операций в соответствии с правилами умножения и деления. Например: - Умножение: 'BCB' * 'C' = 'BCB' + 'BCB' + 'BCB' (1010 * 1 = 1010 + 1010 + 1010 = 11110) - Деление: 'BCB' / 'C' = 'B' (1010 / 1 = 1010) BC-система предоставляет удобный и эффективный метод для выполнения арифметических операций с использованием ограниченного набора символов. Это позволяет сократить количество символов, необходимых для представления чисел, и упростить процесс выполнения арифметических операций. Перевод markdown с английского на русский. Сохранить формулу: Alain Connes Катерина Консани **Перевод с использованием сохранения формул:** A. Коннес: Коллеж де Франс, 3, рю д'Ульм, Париж, Франция, F-75005 [email protected] C. Консани: Математический отдел, Университет Джонса Хопкинса, Балтимор, Мэриленд, 21218, США [email protected] ###### Аннотация. Для каждого простого \( p \) и каждой вложенной \(\sigma\) мультипликативной группы алгебраического замыкания \({\mathbb{F}}_{p}\) в качестве комплексных корней из единицы, мы строим \( p \)-адическое неразложимое представление \(\pi_{\sigma}\) целостной BC-системы как аддитивных эндоморфизмов большого Witt-кольца \(\bar{\mathbb{F}}_{p}\). Полученные представления являются \( p \)-адическими аналогами комплексных, экстремальных KMS\({}_{\infty}\) состояний BC-системы. Роль функции Римана-зета, как функции разбиения BC-системы над комплексными числами \({\mathbb{C}}\), заменяется в \( p \)-адическом случае \( p \)-адическими \( L \)-функциями и полилогарифмами, значения которых на корнях из единицы кодируют KMS состояния. Мы используем теорию Ивасавы для расширения KMS-теории на покрытие завершения \({\mathbb{C}}_{p}\) алгебраического замыкания \({\mathbb{Q}}_{p}\). Мы показываем, что наша предыдущая работа по гиперкольцевой структуре классовой площади коммутаторов, совместно с \( p \)-адическим анализом, позволяет уточнить пространство оценок на циклотомическом расширении \({\mathbb{Q}}\) как некоммутативное пространство, тесно связанное с целостной BC-системой и арифметико-геометрической ориентацией, которая приближается к ожиданиям "арифметического сайта". Наконец, мы объясняем, как целостная BC-система естественным образом возникает также в конструкции стандартной модели \(\bar{\mathbb{F}}_{p}\) де Смита и Ленстры, которая выделяет подсистему, связанную с \(\hat{\mathbb{Z}}\)-расширением \({\mathbb{Q}}\). Ключевые слова и фразы: кольца Витта, конечные поля, BC-система 2000 Классификация математических наук: 11M55, 46L55, 58B34 Авторы частично поддерживаются грантом NSF DMS-FRG-0652164. Первый автор благодарит Ив Андре за полезные предложения. Второй автор хочет поблагодарить Институт высоких научных исследований и Коллеж де Франс за финансовую поддержку. ###### Содержание Содержание * 1 Введение * 2 Функтор \({\mathbb{W}}_{0}\) * 3 Интегральная BC-система * 4 \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) и BC-система * 5 Функтор Виттовых векторов и усеченные квоценты * 6 \(p\)-адические представления \(\pi_{\sigma}\) BC-системы * 7 Теория KMS BC-системы при простом числе \(p\) * 7.1 Автоморфизмы \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) * 7.2 Циклотомические тождества для полилогарифма * 7.3 Линейные формы \(\varphi_{\beta,\rho}\) * 7.4 Условие KMS\({}_{\beta}\) * 7.5 Расширение теории KMS\({}_{\beta}\) на покрытие \({\mathbb{C}}_{p}\) * 8 Расширение \(p\)-адической оценки на \({{\mathbb{Q}}^{\rm cyc}}\) * 9 Проблема базовой точки и "кривая" для глобального поля \({\mathbb{Q}}\) * 9.1 Адельная интерпретация петлевой группоид \(\Pi_{1}^{\rm ab}(X)^{\prime}\) для функциональных полей * 9.2 Волокно над конечным местом \({\mathbb{Q}}\) * 9.3 Волокно над архимедовым местом \({\mathbb{Q}}\) * 9.4 Общая некоммутативная пространственная структура * 9.5 BC-система над \({\mathbb{Z}}\) и \({\mathbb{F}}_{1^{\infty}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}\) * 10 Стандартная модель \(\bar{\mathbb{F}}_{p}\) и BC-система ## 1. Введение Эта статья описывает несколько арифметических свойств системы BC, демонстрируя новые и интересные связи с теорией витовых векторов над алгебраическим замыканием конечных полей и с п-адическим анализом. Система BC - это система квантовой статистической механики, определенная некоммутативной алгеброй Хекке двойных классов в \(P^{+}({\mathbb{Q}})\) относительно подгруппы \(P^{+}({\mathbb{Z}})\), где \(P\subset GL_{2}\) - это алгебраическая группа "ax+b" (_см._[4, 9]). Комплексная алгебра Хекке \({\mathcal{H}}_{\mathbb{C}}\) этой системы имеет очень сложную структуру, поскольку ее регулярное представление, в гильбертовом пространстве односторонних классов, порождает фактор типа III\({}_{1}\) и каноническую "эволюцию по времени" \(\sigma_{t}\in{\rm Aut}({\mathcal{H}}_{\mathbb{C}})\). Изучение состояний равновесия КМС при разных температурах показало арифметическую природу этой динамической системы в свете следующих фактов \(\bullet\) Функция разбиения системы является функцией Римана-зета \(\bullet\) В полюсе функции зета происходит фазовый переход с самопроизвольным нарушением симметрии. \(\bullet\) Вакуумные состояния нулевой температуры реализуют глобальный изоморфизм классовых полей для \({\mathbb{Q}}\). Изучение BC-системы инициировало взаимодействие между теорией чисел и некоммутативной геометрией. Именно некоммутативность алгебры Хекке системы порождает ее нетривиальную динамику. Более того, на некоммутативном пространстве классов аделей \({\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}\), которое естественным образом связано с двойственностью типа II по отношению к BC-системе, можно получить спектральную реализацию нулей \(L\)-функций и интерпретацию следовой формулы явных формул Римана-Вейля (_см_. [7]). Дополнительное исследование (_cf._[15]) показало, что интегральная алгебра Хеке \({\mathcal{H}}_{\mathbb{Z}}={\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\rtimes{ \mathbb{N}}\) предоставляет интегральную модель BC-системы. Эндоморфизмы \(\sigma_{n}(e(r))=e(nr)\), \(n\in{\mathbb{N}}\) действуют на канонические генераторы \(e(r)\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) для \(r\in{\mathbb{Q}}/{\mathbb{Z}}\) и имеют естественные линейные квазиобратные. \[\tilde{\rho}_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\,,\ \ \tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{\prime}=\gamma}e(\gamma^{\prime}),\] (1) которые используются при построении крестового произведения и при представлении алгебры. В этой статье мы устанавливаем для каждого простого числа \(p\) сильную связь между интегральной системой BC и универсальным кольцом Витта \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) алгебраического замыкания простого поля. Конструкция Витта фактически рассматривается в следующих трех различных формах. \(-\) как \(K\)-теоретический эндофунктор \(A\mapsto{\mathbb{W}}_{0}(A)=K_{0}({\mbox{\text@underline{End}}}_{A})/K_{0}(A)\) в категории коммутативных колец (с единицей) \(-\) как большое кольцо Витта \({\mathbb{W}}(A)\) Как функтор \(A\mapsto\mathbb{W}_{p^{\infty}}(A)\), где \(A\) имеет характеристику \(p\). В первых двух случаях ключевые структуры предоставляются следующими операторами. \(-\) мультипликативное поднятие Тайхмюллера \(\tau:A\to{\mathbb{W}}_{0}(A)\) \( - \) Фробениусовым эндоморфизмам \(F_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\), \(n\in{\mathbb{N}}\) \(-\) преобразование Вершевинг, преобразование, сохраняющее аддитивную функциональность \(V_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\), \(n\in{\mathbb{N}}\) \(-\) \(n\)-я компонента призрака \({\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A\), \(n\in{\mathbb{N}}\). Эти основные операторы распространяются от универсального кольца \({\mathbb{W}}_{0}(A)\) до его завершения \({\mathbb{W}}(A)\), элементы которого выражаются витт-векторами, с помощью которых все алгебраические операции можно определить с помощью полиномов с целыми коэффициентами. Это свойство целостности кодирует богатую и глубокую арифметическую информацию. Кроме того, кольцевая структура ограничивается подмножествами, устойчивыми относительно делителей в \({\mathbb{N}}\), что приводит к функтору \({\mathbb{W}}_{p^{\infty}}\) для множества степеней простого числа \(p\). В Предложении 4.4 и Теореме 4.5 мы доказываем, что первичная структура интегральной BC-системы полностью кодируется универсальным кольцом \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), с точным словарём, выражающим основные операторы \(\sigma_{n}\) и \(\tilde{\rho}_{n}\) BC-системы как соответственно Фробениуса \(F_{n}\) и Вершевинга \(V_{n}\) на \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). Изоморфизм, связывающий эти алгебраические структуры, зависит от выбора изоморфизма группы мультипликативной группы \(\bar{\mathbb{F}}_{p}\) с группой _комплексных_ корней из единицы порядка, взаимно простых с \(p\): неопределенность, inherent to this choice is the same as that pertaining to the construction of Brauer lift of characters. Процесс завершения, связанный с включением \({\mathbb{W}}_{0}(A)\subset{\mathbb{W}}(A)\) со сжимающим отображением, затем используется в Теореме 6.4 для получения \(p\)-адического _неразложимого_ представления \(\pi_{\sigma}\) целочисленной BC-системы в качестве аддитивных эндоморфизмов большого кольца Витта \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\), где \(A=\bar{\mathbb{F}}_{p}\) и \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{C}}^{\times}\) - инъективный гомоморфизм групп. Для этого используется установленная тождественность, доказанная в Теореме 4.5, и реализация экспоненциалей Артин-Хассе. Эти представления являются \(p\)-адическими аналогами комплексных, экстремальных состояний KMS\({}_{\infty}\) BC-системы. В разделе 7 эта аналогия развивается гораздо дальше. Реализуя теорию \(p\)-адических \(L\)-функций, мы конструируем аналог, в \(p\)-адическом случае, функции разбиения и состояний KMS\({}_{\beta}\). В частности, мы показываем, что отношения деления для \(p\)-адических полилогарифмов в корнях из единицы соответствуют условию KMS. В §7.5 мы доказываем, что определение функционалов, удовлетворяющих такому условию, распространяется от стандартного "расширенного s-диска" до естественной мультипликативной группы покрытия \({\mathbb{C}}_{p}\). Эти результаты являются \(p\)-адическими аналогами утверждений, доказанных в [17] для функциональных полей. Однако мы также признаём важное отличие с комплексным случаем, а именно наличие добавочной симметрии при ненулевой температуре, вызванной инвариантностью состояний относительно естественной инволюции \({{\mathbb{Q}}^{\rm cyc}}\), которая заменяет каждый корень из единицы его обратным. Эта добавочная симметрия является следствием обращения в ноль \(p\)-адических \(L\)-функций, связанных с нечетными символами Дирихле. Для \(p\) простого числа множество \(X_{p}\) всех инъективных гомоморфизмов групп \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{Q}}/{\mathbb{Z}}\) является параметрическим пространством \(p\)-адических представлений интегральной BC-системы. В разделе 8 мы связываем это множество со пространством \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) расширений \(p\)-адической оценки на максимальное абелево полевое расширение \({{\mathbb{Q}}^{\rm cyc}}\) числового поля \({\mathbb{Q}}\). Мы рассматриваем \({{\mathbb{Q}}^{\rm cyc}}\) как абстрактное поле, определенное как факторгруппа группового кольца \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) по циклотомическому идеалу (_см._ Определение 8.1). Пусть \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) будет подгруппой \({\mathbb{Q}}/{\mathbb{Z}}\) дробей с знаменателем, взаимно простым с \(p\), и пусть \({\mathbb{Q}}^{\rm cyc,p}\) будет подполем (_т.е._ подполем инерции) \({{\mathbb{Q}}^{\rm cyc}}\), порожденным группой \(\mu^{(p)}\sim{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) корней из единицы порядка, взаимно простых с \(p\). Мы описываем канонические изоморфизмы \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) с каждым из следующих пространств \((1)\) Пространство последовательностей неприводимых многочленов \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), удовлетворяющих основным условиям полиномов Конвея (см. Теорема 8.7). \((2)\) Пространство \(\Sigma_{p}\) биекций моноида \({{\mathcal{M}}{(p)}}=\mu^{(p)}\cup\{0\}\), коммутирующих со своими сопряжениями, как в Определении 8.5 (_см._ Предложение 8.8). \((3)\) Пространство \({\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) гомоморфизмов полей, где \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) является подполем разложения, определенным фиксированным полем под действием автоморфизма Фробениуса (_см._ Предложение 8.12). \((4)\) Частное пространства \(X_{p}\) относительно действия \({\rm Gal}(\bar{\mathbb{F}}_{p})\) (_см._ Предложение 8.14). \(5\) Алгебраический спектр фактор-алгебры \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]/J_{p}\), где \(J_{p}\) - это сокращение по модулю \(p\) циклотомического идеала (_см._ Определение 8.1 и Предложение 8.16). Для глобального поля \({\mathbb{K}}\) положительной характеристики (_т.е._ функционального поля, связанного с проективной, негладкой кривой над конечным полем \({\mathbb{F}}_{q}\)), хорошо известно, что пространство оценок максимального абелева расширения \({\mathbb{K}}^{\rm ab}\) над \({\mathbb{K}}\) имеет геометрическое значение. Фактически, для каждого конечного расширения \(E\) из \(\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}}\subset{\mathbb{K}}^{\rm ab}\), пространство \({\rm Val}(E)\) (дискретных) оценок \(E\) является алгебраической одномерной схемой, непустые открытые множества которой являются дополнениями конечных подмножеств \(F\subset{\rm Val}(E)\). Структурный пучок определен локально пересечением \(\bigcap_{F}R\) кольцевых оценок внутри \(E\). Затем пространство \({\rm Val}({\mathbb{K}}^{\rm ab})\) является проективным пределом схем \({\rm Val}(E)\), \(E\subset{\mathbb{K}}^{\rm ab}\). Для глобального поля \({\mathbb{K}}={\mathbb{Q}}\) рациональных чисел, можно рассмотреть его максимальное абелево расширение \({{\mathbb{Q}}^{\rm cyc}}\) как абстрактное поле и попытаться следовать подобной идее. Однако в разделе 9 мы показываем, что пространство \({\rm Val}({{\mathbb{Q}}^{\rm cyc}})\) предоставляет только грубый аналог в характеристике ноль, \({\rm Val}({\mathbb{K}}^{\rm ab})\). Наш подход к этой проблеме опирается на следующие три результата, содержащиеся в нашей предыдущей работе. \((а)\) Аделевая интерпретация петлевого группоида \(\Pi_{1}^{\rm ab}(X)^{\prime}\) абелевого покрытия алгебраической кривой \(X\), связанной с полем функций (_см._[13] и § 9.1) \((b)\) Определение функции подсчета \(N(q)\) (распределения на \([1,\infty)\)), которая заменяет классическую функцию подсчета Вейля для функционального поля при \({\mathbb{K}}={\mathbb{Q}}\) (_см._[11] и § 9.4) \((c)\) Интерпретация функции подсчета \(N(q)\) в качестве числа пересечений, используя действие группы идеальных классов на пространство классов идеалов (_см._ [14]). Применяя эти результаты, мы получаем, что искомое геометрическое волокно над неархимедовым рациональным простым \(p\) является полным пространством главного пучка с основанием \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и группой структуры, заданной связным компактным соленоидом \(S\), определение которого приводится в Утверждении 9.2. Затем, в Утверждении 9.3 мы получаем естественную конструкцию волокна в виде маппинг-торуса \(Y_{p}\) действия Фробениуса на пространство \(X_{p}\). В разделе 9.3 мы рассматриваем волокно \(Y_{\infty}\) над архимедовым простым, с использованием теории мультипликативных норм. Интерпретация, представленная в пункте \((c)\) для функции подсчета в качестве числа пересечений, показывает, что волокна \(Y_{p}\) не должны рассматриваться изолированно, а как часть окружающего не коммутативного пространства, которое отвечает за поперечные факторы, обусловленные архимедовым вкладом в явные формулы. Эта интерпретация подробно разъясняется в разделе 9.4. В разделе 9.5 мы показываем, что интегральная система BC дает для каждого \(p\) (включая архимедово простое) естественное вложение волокна \(Y_{p}\) в некоммутативное пространство, построенное с использованием множества \({\mathcal{E}}({\mathbb{C}}_{p})\) \({\mathbb{C}}_{p}\)-рациональных точек аффинной групповой схемы \({\mathcal{E}}\), которая определяет абелеву часть системы (_см._[15]). Здесь \({\mathbb{C}}_{p}\) обозначает \(p\)-адическое завершение алгебраического замыкания \({\mathbb{Q}}_{p}\). Этот результат показывает, что пространство \[X({\mathbb{C}}_{p}):=\left({\mathcal{E}}({\mathbb{C}}_{p})\times(0,\infty) \right)/({\mathbb{N}}\times\{\pm 1\})\] (2) \[X({\mathbb{C}}_{p}) := \left({\mathcal{E}}({\mathbb{C}}_{p}) \times (0, \infty) \right) / ({\mathbb{N}} \times \{\pm 1\})\] (2) соответствуют, для любого рационального простого числа \(p\), включая \(p=\infty\), определение пространства адельных классов. В Предложении 9.5 мы показываем, используя тот факт, что \({\mathcal{E}}\) является групповой схемой, что \(X({\mathbb{C}}_{p})\) является свободным модулем ранга один над гиперкольцом \({\mathbb{H}}_{\mathbb{Q}}\) адельных классов. Проблема правильной интерпретации связанного фактора \((0,\infty)\) в (2) остается открытой. Это общий принцип, что в наших конструкциях некоммутативные пространства возникают как \(X(A)\) для коммутативного кольца \(A\) (_cf._ (2)), в то время как классические подпространства \(X(A)\) определены как носитель циклотомического идеала (в аффинной схеме \({\mathcal{E}}={\rm Spec}\,({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}])\)). Мы заканчиваем статью, показывая в разделе 10 значимость недавних работ Б. де Смита и Х. Ленстры (_см._ [18]) о "стандартной модели" для алгебраического замыкания конечного поля. Когда \({\mathbb{K}}\) является функциональным полем, промежуточное расширение \({\mathbb{K}}\subset L=\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K }}\subset{\mathbb{K}}^{\rm ab}\) играет важную геометрическую роль, а именно, расширение скаляров до алгебраически замкнутого поля для алгебраической кривой, связанной с \({\mathbb{K}}\). Когда \({\mathbb{K}}={\mathbb{Q}}\), мы показываем, что промежуточное расширение \({\mathbb{Q}}\subset{{\mathbb{Q}}^{\rm cycl}_{\Delta}}\subset{{\mathbb{Q}}^{\rm cyc}}\), используемое де Смитом и Ленстрой, очень близко подходит к ожидаемым свойствам для аналогичного промежуточного расширения \({\mathbb{Q}}\subset L\subset{{\mathbb{Q}}^{\rm cyc}}\). Их построение предоставляет концептуальное построение подполя \(\bar{\mathbb{F}}_{p}\), объединяющего все расширения, степень которых взаимно проста с \(p\). В самой последней части статьи мы напоминаем об одном из первых применений, предоставленных Э. Виттом, своего функтора, который представляет концептуальное построение недостающего куска \(\bigcup_{n}{\mathbb{F}}_{p^{p^{n}}}\subset\bar{\mathbb{F}}_{p}\), используя простое уравнение \(X^{p}=X+1\) в векторах Витта. ## 2. Функтор \({\mathbb{W}}_{0}\) В данном разделе мы вспомним определение и основные свойства универсального кольца \({\mathbb{W}}_{0}(A)\), где \(A\) - любое коммутативное кольцо с единицей. Дополнительные детали можно найти в [1]. Вторая часть раздела описывает \({\mathbb{W}}_{0}(k)\) для алгебраически замкнутого поля \(k\). Пусть \({\mbox{\textunderline{End}}}_{A}\) (или \(\text{End}~{}{\mathcal{P}}(A)\)) - это категория эндоморфизмов проективных \(A\)-модулей конечного ранга. Объектами являются пары \((E, f)\), где \(E\) - конечный проективный \(A\)-модуль, а \(f\in{\mbox{End}}_{A}(E)\). Морфизмы в этой категории должны коммутировать с эндоморфизмами \(f\). Следующие операции - операция прямой суммы и тензорного произведения. \[(E_{1},f_{1})\oplus(E_{2},f_{2})=(E_{1}\oplus E_{2},f_{1}\oplus f_{2})\,,\ \ ( E_{1},f_{1})\otimes(E_{2},f_{2})=(E_{1}\otimes E_{2},f_{1}\otimes f_{2})\] (3) превратить группу Гротендика \(K_{0}({\mbox{\text@underline{End}}}_{A})\) в (коммутативное) кольцо. Пары вида \((E,f=0)\) порождают идеал \(K_{0}(A)\subset K_{0}({\mbox{\text@underline{End}}}_{A})\). Мы обозначаем факторкольцо через \({\mathbb{W}}_{0}(A)\) \[{\mathbb{W}}_{0}(A)=K_{0}({\mbox{\text@underline{End}}}_{A})/K_{0}(A).\] (4) \[\mathbb{W}_{0}(A)=K_{0}(\underline{\text{End}}_{A})/K_{0}(A).\] (4) По определению, \({\mathbb{W}}_{0}\) является эндофунктором категории \(\mathfrak{Ring}\) коммутативных колец с единицей. На \({\mathbb{W}}_{0}\) действуют несколько ключевых операторов и отображений, следующие из них являются наиболее значимыми для наших приложений. \((1)\) Подъем Тейхмюллера \(\tau:A\to{\mathbb{W}}_{0}(A)\), который является мультипликативным отображением. \((2)\) Для \(n\in{\mathbb{N}}\), кольцевые эндоморфизмы Фробениуса \(F_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\). \((3)\) Для \(n\in{\mathbb{N}}\) Вершубунг (сдвиг) аддитивный функториальный отображения \(V_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A)\). \((4)\) Для \(n\in{\mathbb{N}}\), \(n\)-тая гомоморфизм компонента приведенной группы \({\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A\). Мы кратко вспомним их определения. \((1)\) Тейхмюллеров подъем \(\tau=[\cdot]:A\to{\mathbb{W}}_{0}(A)\) определяется как \(f\mapsto\tau(f)=[f]=(A,f)\). \((2)\) Для \(n\in{\mathbb{N}}\) операции в \({\mbox{\text@underline{End}}}_{A}\), при возведении эндоморфизма \(f\) в \(n\)-ую степень, порождают Frobenius-эндоморфизмы кольца в \({\mathbb{W}}_{0}(A)\) \[F_{n}:{\mathbb{W}}_{0}(A)\rightarrow{\mathbb{W}}_{0}(A),\qquad F_{n}(E,f)=(E,f^{n}).\] (5) \((3)\) Для \(n\in{\mathbb{N}}\) отображения Вершубунг определены следующими операциями над матрицами \[V_{n}:{\mathbb{W}}_{0}(A)\to{\mathbb{W}}_{0}(A),\qquad V_{n}(E,f)=(E^{\oplus n },\begin{bmatrix}0&0&\cdots&\cdots&f\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}).\] (6) \((4)\) Для \(n\in{\mathbb{N}}\), компоненты призрака задаются \[{\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A,\quad{\rm gh}_{n}(E,f)={\rm Trace}(f^{n}).\] (7) \[{\rm gh}_{n}:{\mathbb{W}}_{0}(A)\to A,\quad{\rm gh}_{n}(E,f)={\rm Trace}(f^{n}).\] (7) Пусть \(\Lambda(A):=1+tA[[t]]\) - это мультипликативная абелева группа формальных степенных рядов с постоянным членом \(1\). (Обратное) характеристическое уравнение определяет гомоморфизм абелевых групп. \[L:{\mathbb{W}}_{0}(A)\to\Lambda(A),\quad L(E,f)=\det(1-tM(f))^{-1}\] (8) Это выражение не требует перевода, так как является математическим выражением и сохраняет свою форму независимо от языка. где \(M(f)=(a_{ij})\) - матрица, связанная с \(f:E\to E\) (_т.е._\(f~{}\leftrightarrow~{}\sum_{i}x_{i}^{*}\otimes x_{i}\), \(x_{i}^{*}\in E^{*},x_{i}\in E\), \(a_{ij}=\langle x_{i}^{*},x_{j}\rangle\)). По фундаментальному результату G. Almkvist ([1] Теорема 6.4 или [2] Главная Теорема), имеется **Теорема 2.1.**: _Отображение \(L\) инъективно, и его образ является подгруппой \(\Lambda(A)\)_. \[{\rm Диапазон}(L)=\left\{\frac{{1+a_{1}t+\ldots+a_{n}t^{n}}}{{1+b_{1}t+\ldots+b_{n}t^{n}}}\mid a _{j},b_{j}\in A\right\}.\] (9) Обратите внимание, что для \(E\) конечного проективного \(A\)-модуля и \(f,g\in{\mbox{End}}_{A}(E)\) имеем \[(E,fg)=(E,gf)\in{\mathbb{W}}_{0}(A).\] (10) \[(E,fg)=(E,gf)\in{\mathbb{W}}_{0}(A).\] (10) Однако у нас есть: \[V_{nm}=V_{n}\circ V_{m}=V_{m}\circ V_{n}\,,\ \ F_{nm}=F_{n}\circ F_{m}=F_{m} \circ F_{n}.\] (11) \[V_{nm}=V_{n}\circ V_{m}=V_{m}\circ V_{n}\,,\ \ F_{nm}=F_{n}\circ F_{m}=F_{m} \circ F_{n}.\] (11) Следующее предложение собирает вместе несколько стандартных уравнений, связывающих эти операторы. **Утверждение 2.2**: _Пусть \(A\) - коммутативное кольцо, а \(x,y\in{\mathbb{W}}_{0}(A)\). Выполняются следующие равенства._ \((1)\) \(F_{n} \circ V_{n}(x) = nx\). \((2)\)_\(V_{n}(F_{n}(x)y)=xV_{n}(y)\)_ \((3)\) _Если \((m,n)=1\), то \(V_{m}\circ F_{n}=F_{n}\circ V_{m}\)._ \((4)\) _Для \(n\in{\mathbb{N}}\), \(V_{n}(x)V_{n}(y)=nV_{n}(xy)\)._ \((5)\) _Для \(n\in{\mathbb{N}}\), \(F_{n}(\tau(f))=\tau(f^{n})\)._ \((6)\) _Для \(n,m\in{\mathbb{N}}\), \({\rm gh}_{n}(F_{m}(f))={\rm gh}_{nm}(f)\)._ \((7)\)_\({\rm gh}_{n}(V_{m}(f))=\begin{cases}m\,{\rm gh}_{n/m}(f)&\text{если $m|n$}\\ 0&\text{в противном случае.}\end{cases}\)_ Доказательство: Все доказательства прямолинейны, мы просто проверяем \((4)\) в качестве примера. Для \(x\in{\mbox{End}}_{A}(E)\), действие \(X=V_{n}(E,x)\) на векторы \(\xi=(\xi_{1},\ldots,\xi_{n})\in E^{\oplus n}\) задается \[(X\xi)_{1}=x\xi_{n}\,,\ \ (X\xi)_{j}=\xi_{j-1}\,,\quad~{}\forall j,~{}2\leq j \leq n.\] translates to: \[(X\xi)_{1}=x\xi_{n}\,,\ \ (X\xi)_{j}=\xi_{j-1}\,,\quad~{} \forall j,~{}2\leq j \leq n.\] Аналогичные формулы справедливы для \(Y=V_{n}(F,y)\), для \(y\in{\mbox{End}}_{A}(F)\). По определению, \(V_{n}(x)V_{n}(y)\) соответствует \(X\otimes Y\in{\mbox{End}}_{A}(E^{\oplus n}\otimes F^{\oplus n})\). Этот эндоморфизм разлагается в прямую сумму \(n\) эндоморфизмов \((E\otimes F)^{\oplus n}\), каждый из которых имеет вид \[\begin{bmatrix}0&0&\cdots&\cdots&x\otimes 1\\ 1&0&0&\cdots&0\\ 0&1\otimes y&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix},\quad\text{или}\quad\begin{bmatrix}0&0&\cdots&\cdots&x \otimes y\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}.\] Применяя (10), можно убедиться, что каждое из указанных эндоморфизмов эквивалентно \(V_{n}(x\otimes y)\). Следовательно, выполняется равенство \(V_{n}(x)V_{n}(y)=nV_{n}(xy)\). ∎ Мы применим следующее предложение к случаю \(A=k=\bar{\mathbb{F}}_{p}\), где \(\bar{\mathbb{F}}_{p}\) - алгебраическое замыкание \({\mathbb{F}}_{p}\). **Утверждение 2.3.**: _Пусть \(k\) - алгебраически замкнутое поле. Тогда отображение, сопоставляющее \((E,f)\) из \(\mbox{\text@underline{End}}_{k}\) делителю \(\delta(f)\) ненулевых собственных значений \(f\) (с учетом кратности), продолжается до изоморфизма колец_. \[\delta:{\mathbb{W}}_{0}(k)\stackrel{{\sim}}{{\to}}{\mathbb{Z}}[k^{ \times}].\] (12) \[\delta:{\mathbb{W}}_{0}(k)\stackrel{{\sim}}{{\rightarrow}}{\mathbb{Z}}[k^{ \times}].\] (12) Под вышеприведенным изоморфизмом Фробениус \(F_{n}\) на \({\mathbb{W}}_{0}(k)\) определяется на \({\mathbb{Z}}[k^{\times}]\) естественной линейной формализацией группового эндоморфизма \(k^{\times}\to k^{\times},~{}g\mapsto g^{n}\). Доказательство: Применяя Теорему 2.1, характеристический полином расширяется до полного инварианта на \(K_{0}({\mbox{\text@underline{End}}}_{k})\) и до изоморфизма \(K_{0}({\mbox{\text@underline{End}}}_{k})\) с кольцом частных монических полиномов в \(k[t]\). Модификация этого кольца по \(K_{0}(k)\) означает удаление степеней переменной. Таким образом, делитель ненулевых собственных значений \(f\) расширяется, чтобы определить взаимно однозначное соответствие между множествами \({\mathbb{W}}_{0}(k)\simeq{\mathbb{Z}}[k^{\times}]\). Остаётся проверить, что эта биекция сохраняет операции кольца. Для сложения, множество, лежащее в основе делителя \(\delta(f_{1}+f_{2})\), является объединением двух множеств корней \(f_{j}\), и, следовательно, \(\delta(f_{1}+f_{2})=\delta(f_{1})+\delta(f_{2})\). Для произведения достаточно и легко проверить, что тензорное произведение двух элементов ранга один \((k,a)\otimes(k,b)\) равно \((k,ab)\) для ненулевых элементов \(k\). Утверждение о \(F_{n}\) проверяется аналогичным образом, используя (5) на элементах \((k,a)\). ∎ Мы напоминаем следующую формулу для \(L(f)\) в терминах делителя \(\delta(f)=\sum n(\alpha)[\alpha]\in{\mathbb{Z}}[k^{\times}]\) \[L(f)=\prod(1-\alpha\,t)^{-n(\alpha)}.\] (13) → \[L(f)=\prod(1-\alpha\,t)^{-n(\alpha)}.\] (13) **Следствие 2.4**: _Для любого заданного изоморфизма \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\stackrel{{\sim}}{{ \longrightarrow}}{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) мультипликативной группы алгебраического замыкания \(\bar{\mathbb{F}}_{p}\) с подгруппой \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{\mathbb{Z}}\) дробей с знаменателем взаимно простым с \(p\), получается изоморфизм_ \[ \tilde{\sigma}:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\stackrel{{ \sim}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]. \] (14) _Под изоморфизмом \(\tilde{\sigma}\), Фробениус \(F_{n}\) из \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) действует на \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) естественной линеаризацией группового эндоморфизма \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), \(g\mapsto g^{n}\) (т.е. \(\gamma\mapsto n\gamma\) в аддитивной нотации)._ ## 3. Интегральная система BC Для каждого \(n\in{\mathbb{N}}\) определяются эндоморфизмы кольца группы \[\sigma_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{\mathbb{Q}} /{\mathbb{Z}}],\qquad\sigma_{n}(e(\gamma))=e(n\gamma)\] \begin{align*} \sigma_{n} & :{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}] \to {\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}], \\ \sigma_{n}(e(\gamma)) & =e(n\gamma) \end{align*} и следующие аддитивные отображения \[\tilde{\rho}_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],\qquad\tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{ \prime}=\gamma}e(\gamma^{\prime}).\] (15) (Russian translation) \[\tilde{\rho}_{n}:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],\qquad\tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{ \prime}=\gamma}e(\gamma^{\prime}).\] (15) Мы вспоминаем из [15], Предложение 4.4, следующий результат **Утверждение 3.1**: _Андоморфизмы \(\sigma_{n}\) и отображения \(\tilde{\rho}_{m}\) удовлетворяют следующим соотношениям_ \[\sigma_{nm}=\sigma_{n}\sigma_{m}\,,\ \ \tilde{\rho}_{mn}=\tilde{\rho}_{m} \tilde{\rho}_{n}\,,\quad~{}\forall m,n\in{\mathbb{N}}\] (16) \[\sigma_{nm}=\sigma_{n}\sigma_{m}\,,\ \ \tilde{\rho}_{mn}=\tilde{\rho}_{m} \tilde{\rho}_{n}\,,\quad~{}\forall m,n\in{\mathbb{N}}\] (16) \[\tilde{\rho}_{m}(\sigma_{m}(x)y)=x\tilde{\rho}_{m}(y)\,,\quad~{}\forall x,y\in {\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\] (17) \[\tilde{\rho}_{m}(\sigma_{m}(x)y)=x\tilde{\rho}_{m}(y)\,,\quad~{}\forall x,y\in {\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\] (17) \[\sigma_{c}(\tilde{\rho}_{b}(x))=(b,c)\,\tilde{\rho}_{b^{\prime}}(\sigma_{c^{ \prime}}(x))\,,\ \ b^{\prime}=b/(b,c)\,,\ \ c^{\prime}=c/(b,c)\,,\] (18) \[\sigma_{c}(\tilde{\rho}_{b}(x))=(b,c)\,\tilde{\rho}_{b^{\prime}}(\sigma_{c^{ \prime}}(x))\,,\ \ b^{\prime}=b/(b,c)\,,\ \ c^{\prime}=c/(b,c)\,,\] (18) _где \((b,c)=\text{НОД}(b,c)\)._ Обратите внимание, что при \(b=c=n\) в (18) получается \[\sigma_{n}(\tilde{\rho}_{n}(x))=n\,x\,,\quad~{}\forall x\in{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}].\] (19) \[\sigma_{n}(\tilde{\rho}_{n}(x))=n\,x\,,\quad~{}\text{для всех}~{}x\in{\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}].\] (19) Наоборот, если мы возьмем \(b=n\) и \(c=m\) взаимно простыми числами, то получим \[\sigma_{n}\circ\tilde{\rho}_{m}=\tilde{\rho}_{m}\circ\sigma_{n}.\] (20) \[\sigma_{n}\circ\tilde{\rho}_{m}=\tilde{\rho}_{m}\circ\sigma_{n}.\] (20) Мы напоминаем из [15] (Определение 4.7 и §4.2) следующие факты. Интегральная \(BC\)-алгебра - это алгебра \({\mathcal{H}}_{\mathbb{Z}}={\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\rtimes_{ \tilde{\rho}}{\mathbb{N}}\), порождённая групповым кольцом \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) и элементами \(\tilde{\mu}_{n}\) и \(\mu_{n}^{*}\), где \(n\in{\mathbb{N}}\), которые удовлетворяют следующим соотношениям: \[\begin{array}[]{l}\tilde{\mu}_{n}x\mu_{n}^{*}=\tilde{\rho}_{n}(x)\\[8.535827pt ] \mu_{n}^{*}x=\sigma_{n}(x)\mu_{n}^{*}\\[8.535827pt] x\tilde{\mu}_{n}=\tilde{\mu}_{n}\sigma_{n}(x),\end{array}\] (21) где \(\tilde{\rho}_{m}\), \(m\in{\mathbb{N}}\) определено в (15), а также отношения \[\begin{array}[]{l}\tilde{\mu}_{nm}=\tilde{\mu}_{n}\tilde{\mu}_{m}\,,\quad~{} \forall n,m\in{\mathbb{N}}\\[8.535827pt] \mu_{nm}^{*}=\mu_{n}^{*}\mu_{m}^{*}\,,\quad~{}\forall n,m\\[8.535827pt] \mu_{n}^{*}\tilde{\mu}_{n}=n\\[8.535827pt] \tilde{\mu}_{n}\mu_{m}^{*}=\mu_{m}^{*}\tilde{\mu}_{n}\ \ \ \ (n,m)=1.\end{array}\] (22) После тензорного произведения на \({\mathbb{Q}}\), алгебра Хекке \({\mathcal{H}}_{\mathbb{Q}}={\mathcal{H}}_{\mathbb{Z}}\otimes_{\mathbb{Z}}{ \mathbb{Q}}\) имеет более простое явное представление с генераторами \(\mu_{n}(=\frac{1}{n}\tilde{\mu}_{n})\), \(\mu_{n}^{*}\), \(n\in{\mathbb{N}}\) и \(e(r)\), для \(r\in{\mathbb{Q}}/{\mathbb{Z}}\), удовлетворяющими соотношениям \(\bullet\)\(\mu_{n}^{*}\mu_{n}=1\), \(\forall n\in{\mathbb{N}}\) \(\bullet\)\(\mu_{m}\mu_{n}=\mu_{mn}\), \(\mu^{*}_{m}\mu^{*}_{n}=\mu^{*}_{mn}\), \(\forall m,n\in{\mathbb{N}}\), \(\bullet\)\(\mu_{m}\mu_{n}=\mu_{mn}\), \(\mu^{*}_{m}\mu^{*}_{n}=\mu^{*}_{mn}\), \(\forall m,n\in{\mathbb{N}}\), \(\bullet\) \(\mu_{n}\mu_{m}^{*}=\mu_{m}^{*}\mu_{n}\), если \((n,m)=1\), \(\bullet\) \(e(0)=1\), \(e(r)^{*}=e(-r)\), и \(e(r)e(s)=e(r+s)\), \(\forall r,s\in{\mathbb{Q}}/{\mathbb{Z}}\) \(\bullet\) Для всех \(n\in{\mathbb{N}}\) и всех \(r\in{\mathbb{Q}}/{\mathbb{Z}}\) \[\mu_{n}\,e(r)\,\mu_{n}^{*}=\frac{1}{n}\sum_{ns=r}e(s).\] (23) \[\mu_{n}\,e(r)\,\mu_{n}^{*}=\frac{1}{n}\sum_{ns=r}e(s).\] (23) После тензорного произведения с \({\mathbb{C}}\) и завершения получается \(C^{*}\)-алгебра с естественной временной эволюцией \(\sigma_{t}\) ([4], [16], глава III). Экстремальные состояния KMS ниже критической температуры исчезают на мономах \(\mu_{n}x\mu_{m}^{*}\) для \(n\neq m\) и \(x\in{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\), и их значение на \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) задается \[\varphi_{\beta,\rho}(e(a/b))=\frac{1}{\zeta(\beta)}\sum_{n=1}^{\infty}n^{- \beta}\rho(\zeta_{a/b}^{n}),\] (24) где \(\rho\in\hat{\mathbb{Z}}^{*}\) определяет вложение в \({\mathbb{C}}\) циклотомического поля \({{\mathbb{Q}}^{\rm cyc}}\), порожденного абстрактными корнями из единицы. ## 4. \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) и BC-система В [29] Квиллен использует выбор вложения. \[ \sigma : \overline{\mathbb{F}}_{p}^{\times} \rightarrow \mathbb{C}^{\times} \] (25) \[\sigma : \overline{\mathbb{F}}_{p}^{\times} \rightarrow \mathbb{C}^{\times} \] (25) в изучении алгебраической K-теории общей линейной группы над конечным полем. В этом разделе мы сравниваем описание универсального кольца Витта \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), обладающего структурой, заданной морфизмами Фробениуса \(F_{n}\) и отображениями Вершебунга \(V_{n}\) с интегральной BC-алгеброй \({\mathcal{H}}_{\mathbb{Z}}\). При простом процессе сравнения мы замечаем, что отношения (16), (17), (18), справедливые для \({\mathcal{H}}_{\mathbb{Z}}\), те же самые, что и для эндоморфизмов Фробениуса \(F_{n}\) и отображений Вершубунга \(V_{n}\) на \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). Более точно, при соответствиях \(\sigma_{n}\to F_{n}\), \(\tilde{\rho}_{n}\to V_{n}\) два отношения из (11) соответствуют (16), и первые три отношения Proposition 2.2 соответствуют соответственно (19), (17) и (20). Эти результаты явно указывают на существование сильной связи между (\(\lambda\))-кольцом \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) и групповым кольцом \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), наделенным упомянутыми операторами. Затем мы сравниваем две групповые кольца: \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) и \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), которые возникают в описании \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) и в построении BC-алгебры соответственно. Существует сюръективный гомоморфизм групп: \({\mathbb{Q}}/{\mathbb{Z}}\to{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), индуцированный каноническим факторизацией групп. \[{ \mathbb{Q} }/{ \mathbb{Z} }={({ \mathbb{Q} }/{ \mathbb{Z} })^{(p)}}\times{ \mathbb{Q} }_{p}/{ \mathbb{Z} }_{p}\] (26) , где \({\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}\) является группой дробей, у которых знаменатель является степенью \(p\). Таким образом, получается соответствующая факторизация колец. \[{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]={\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z }})^{(p)}}]\otimes_{\mathbb{Z}}{\mathbb{Z}}[{\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}].\] (27) \[\mathbb{Z}[{\mathbb{Q}}/{\mathbb{Z}}]={\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z }})^{(p)}}]\otimes_{\mathbb{Z}}{\mathbb{Z}}[{\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}].\] (27) Используя тривиальное представление \({\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}\) (т.е. авгментацию \(\epsilon\) из \({\mathbb{Z}}[{\mathbb{Q}}_{p}/{\mathbb{Z}}_{p}]\)), получается ретракция \(r=id\otimes\epsilon\), создающая расщепление. \[\mathbb{Z}[{(\mathbb{Q}/\mathbb{Z})^{(p)}}] \stackrel{{j_{p}}}{{\longrightarrow}} \mathbb{Z}[\mathbb{Q}/\mathbb{Z}] \stackrel{{id\otimes\epsilon}}{{\longrightarrow}} \mathbb{Z}[{(\mathbb{Q}/\mathbb{Z})^{(p)}}].\] (28) Обратите внимание, что действие отображения \(\gamma\mapsto n\gamma\), \(\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), сохраняет \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Это означает, что эндоморфизмы \(\sigma_{n}\), действующие на BC-алгебре, естественным образом ограничиваются для определения эндоморфизмов \(\sigma_{n}:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Z}}[{( {\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\). Давайте обозначим \(I(p)\subset{\mathbb{N}}\) множество целых чисел, которые взаимно просты с \(p\). Следующая лемма описывает проекцию операторов \(\tilde{\rho}_{n}\) алгебры BC на групповое кольцо \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\). **Утверждение 4.1**: _Пусть \(n=p^{k}m\), где \(m\in I(p)\). Для \(\gamma\in{\mathbb{Q}}/{\mathbb{Z}}\), мы можем записать по модулю \(1\)_. \[\gamma=\frac{a}{b}+\frac{c}{p^{s}}\,,\ b\in I(p)\,,\ a,b,c,s\in{\mathbb{N}}.\] (29) \[\gamma=\frac{a}{b}+\frac{c}{p^{s}}\,,\ b\in I(p)\,,\ a,b,c,s\in{\mathbb{N}}.\] (29) _Потом, с \(\tilde{\rho}_{n}\) таким, как в (15), у нас есть_ \[r\circ\tilde{\rho}_{n}(e(\gamma))=p^{k}\sum_{w=0}^{m-1}e(\frac{f+wb}{bm})\] (30) _где \(y=\frac{f}{bm}\), \(f\in{\mathbb{Z}}/bm{\mathbb{Z}}\), является единственным решением в \({\mathbb{Q}}/{\mathbb{Z}}\), с знаменателем, взаимнопростым с \(p\), уравнения_ The translation of the given markdown to Russian is: \[ p^{k}y=\frac{a}{bm}\in{\mathbb{Q}}/{\mathbb{Z}}. \qquad (31) \] Доказательство. Существование и единственность разложения (29) вытекает из факторизации (26). Для \(d\in I(p)\), эндоморфизм \({\mathbb{Q}}/{\mathbb{Z}}\): \(x\mapsto px\) ограничивается автоморфизмом на подгруппе \(G_{d}=\{\frac{a}{d}\in{\mathbb{Q}}/{\mathbb{Z}}|\,a\in{\mathbb{Z}}\}\subset{ \mathbb{Q}}/{\mathbb{Z}}\). Для \(d=bm\), этот факт показывает существование и единственность решения \(y=\frac{f}{bm}\) уравнения (31). Для некоторого целого \(j\in{\mathbb{Z}}\), имеем \(p^{k}y=\frac{a}{bm}+j\), тем самым. \[y=\frac{a}{bmp^{k}}+\frac{j}{p^{k}}=\frac{a}{bn}+\frac{j}{p^{k}},\ \ ny=\frac{ a}{b}+jm.\] \[y=\frac{a}{bmp^{k}}+\frac{j}{p^{k}}=\frac{a}{bn}+\frac{j}{p^{k}},\ \ ny=\frac{ a}{b}+jm.\] Путем применения (26) также имеется разложение следующего вида \[\frac{c}{np^{s}}=\frac{c}{mp^{s+k}}=\frac{d}{m}+\frac{e}{p^{s+k}}.\] (32) \[\frac{c}{np^{s}}=\frac{c}{mp^{s+k}}=\frac{d}{m}+\frac{e}{p^{s+k}}.\] (32) Один имеет \(ny=\frac{a}{b}\) по модулю \(1\), \(n\frac{c}{np^{s}}=\frac{c}{p^{s}}\), поэтому решения уравнения \(n\gamma^{\prime}=\gamma\) в \({\mathbb{Q}}/{\mathbb{Z}}\), которые входят в (15), имеют форму \[\gamma^{\prime}=y+\frac{c}{np^{s}}+\frac{u}{m}+\frac{v}{p^{k}}\,,\ \ u\in\{0, \ldots,m-1\}\,,\ v\in\{0,\ldots,p^{k}-1\}.\] Используя (32), получаем \[\gamma^{\prime}=y+\frac{u}{m}+\frac{d}{m}+\frac{v}{p^{k}}+\frac{e}{p^{s+k}}\,, \ \ u\in\{0,\ldots,m-1\}\,,\ v\in\{0,\ldots,p^{k}-1\}\] Для проекции \(r(e(\gamma^{\prime}))\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\), следовательно, получается, что \[r(e(\gamma^{\prime}))=e(y+\frac{w}{m})=e(\frac{f+wb}{bm})\,, \ \ w\in\{0,\ldots ,m-1\}\] которое повторяется с кратностью \(p^{k}\). Следует уравнение (30). ∎ **Следствие 4.2.**: _У нас есть_ \[\displaystyle r\circ\tilde{\rho}_{n}(x)= r\circ\tilde{\rho}_{n}(r(x))\,,\quad~{}\forall x\in{ \mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\,,\ n\in{\mathbb{N}}.\] (33) _и_ \[r\circ\tilde{\rho}_{p^{k}}(x) = p^{k}\sigma_{p^{k}}^{-1}(r(x))\,,\quad \forall x \in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],~{}k\in{\mathbb{N}}\,.\] (34) Доказательство.: Оба утверждения следуют из (30).∎ **Определение 4.3**. _Для \(p\) простого числа мы обозначаем через \(X_{p}\) пространство всех инъективных гомоморфизмов группы \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{Q}}/{\mathbb{Z}}\)._ Связь между \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) и абелевой частью \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) целочисленной BC-алгебры \({\mathcal{H}}_{\mathbb{Z}}\) описывается следующей леммой. **Утверждение 4.4.**: _Пусть \(\sigma\in X_{p}\) и пусть \(\tilde{\sigma}\) будет связанным изоморфизмом колец_ \[\tilde{\sigma}:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\stackrel{{ \sim}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] \subset{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}].\] Перевод: \[\tilde{\sigma}:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\stackrel{{ \sim}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] \subset{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}].\] _Затем ограничение кольцевых эндоморфизмов \(\sigma_{n}\) и отображений \(\tilde{\rho}_{n}\) на \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) по формулам дают Фробениус \(F_{n}\) и отображение Verschiebung \(V_{n}\) на \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\)._ \[\tilde{\sigma}\circ F_{n}=\sigma_{n}\circ\tilde{\sigma}\,,\ \ \tilde{\sigma} \circ V_{n}=r\circ\tilde{\rho}_{n}\circ\tilde{\sigma}.\] (35) \[\tilde{\sigma}\circ F_{n}=\sigma_{n}\circ\tilde{\sigma}\,,\ \ \tilde{\sigma} \circ V_{n}=r\circ\tilde{\rho}_{n}\circ\tilde{\sigma}.\] (35) Доказательство.: В разделе 2 мы вспомнили (_см._ [19] для подробностей), что Фробениус \(F_{n}\) на \({\mathbb{W}}_{0}(A)\) задается как \(F_{n}(E,f)=(E,f^{n})\). На уровне делителя собственных значений \(f\) (виртуальном случае это делитель), _т.е._ на уровне соответствующего элемента в \({\mathbb{Z}}[k^{\times}]\), где \(A=k=\bar{\mathbb{F}}_{p}\), Фробениус \(F_{n}\) соответствует гомоморфизму группы \(g\mapsto g^{n}\) (_см._ Предложение 2.3). Отображения Вершибунга \(V_{n}\) описываются операцией (6) на матрицах. Отображения \(V_{n}\) являются аддитивными и, следовательно, определены элементами \(V_{n}([\alpha])\), где \(\alpha\in k^{\times}\). Они соответствуют \(n\) собственным значениям следующей матрицы \[V_{n}(\alpha)=\begin{bmatrix}0&0&\cdots&\cdots&\alpha\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}.\] translates to \[V_{n}(\alpha)=\begin{bmatrix}0&0&\cdots&\cdots&\alpha\\ 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ 0&0&0&1&0\end{bmatrix}.\] Так как \(n\)-я степень данной матрицы является умножением на \(\alpha\), все её собственные значения удовлетворяют уравнению \(\beta^{n}=\alpha\). Фактически, характеристический полином данной матрицы имеет вид \(P(X)=X^{n}-\alpha\). Пусть \(n=p^{k}m\), где \(m\) взаимно просто с \(p\). Так как \(\bar{\mathbb{F}}_{p}\) является совершенным полем, корень \(\alpha^{p^{-k}}\in\bar{\mathbb{F}}_{p}\) уравнения \(X^{p^{k}}-\alpha\) является единственным и имеет \(m\) различных корней порядка \(m\): \(\beta^{m}=\alpha^{p^{-k}}\), которые являются \(m\) корнями полинома \(P(X)\). Они имеют вид \(\xi\beta_{0}\), где \(\xi^{m}=1\). Таким образом, соответствующий делитель - \[\delta=\sum_{\xi^{m}=1}p^{k}[\xi\beta_{0}].\] (36) \[\delta=\sum_{\xi^{m}=1}p^{k}[\xi\beta_{0}].\] (36) Мы сравниваем описание делителя, связанного с \(V_{n}(E,f)\), с \(r\circ\tilde{\rho}_{n}(e(\gamma))\), где \(\gamma=\sigma(\alpha)=\frac{a}{b}\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset {\mathbb{Q}}/{\mathbb{Z}}\). Элементы \(\xi\beta_{0}\in\bar{\mathbb{F}}_{p}\) являются \(m\) различными корнями уравнения \(X^{n}=\alpha\). Аналогично, с обозначениями из (30), элементы \[\frac{f+wb}{bm}\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{ \mathbb{Z}},\ \ w\in\{0,\ldots,m-1\}\] will be translated as: \[\frac{f+wb}{bm}\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{ \mathbb{Z}},\ \ w\in\{0,\ldots,m-1\}\] являются \(m\) решениями в \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) уравнения \(nz=\gamma\). Получается \[\tilde{\sigma}(\delta) = p^{k}\sum_{w=0}^{m-1}e(\frac{f+wb}{bm}).\] Таким образом (30) показывает, что \[\tilde{\sigma}(V_{n}([\alpha]))=\tilde{\sigma}(\delta)=r\circ\tilde{\rho}_{n}( e(\gamma))=r\circ\tilde{\rho}_{n}\circ\tilde{\sigma}([\alpha]).\] \[\tilde{\sigma}(V_{n}([\alpha]))=\tilde{\sigma}(\delta)=r\circ\tilde{\rho}_{n}( e(\gamma))=r\circ\tilde{\rho}_{n}\circ\tilde{\sigma}([\alpha]).\] ∎ **Теорема 4.5****.**: _Пусть \(\sigma\in X_{p}\). Следующие формулы определяют представление \(\pi_{\sigma}\) интегральной BC-системы \({\mathcal{H}}_{\mathbb{Z}}\) как аддитивных эндоморфизмов \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\)_ \[\pi_{\sigma}(x)\xi=\tilde{\sigma}^{-1}(r(x))\,\xi\,,\ \ \pi_{\sigma}(\mu_{n}^{ *})=F_{n}\,,\ \ \pi_{\sigma}(\tilde{\mu}_{n})=V_{n}\] (37) \[\pi_{\sigma}(x)\xi=\tilde{\sigma}^{-1}(r(x))\,\xi\,,\ \ \pi_{\sigma}(\mu_{n}^{ *})=F_{n}\,,\ \ \pi_{\sigma}(\tilde{\mu}_{n})=V_{n}\] (37) _для всех \(\xi\in{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) и \(n\in{\mathbb{N}}\)._ Доказательство: По построению \(x\mapsto\tilde{\sigma}^{-1}(r(x))\) является гомоморфизмом группового кольца \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) в \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\), и, следовательно, композиция с левым регулярным представлением \(\pi_{\sigma}\) задает представление \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\). \(F_{n}\) и \(V_{n}\) являются аддитивными. Остается проверить соотношения (21) и (22). Первые две следуют из (11), а последние две - из \((1)\) и \((3)\) Предложения 2.2. Чтобы проверить первое соотношение из (21), необходимо показать, что \[V_{n}\pi_{\sigma}(x)F_{n}=\pi_{\sigma}(\tilde{\rho}_{n}(x)).\] (38) \[V_{n}\pi_{\sigma}(x)F_{n}=\pi_{\sigma}(\tilde{\rho}_{n}(x)).\] (38) Один имеет \(\pi_{\sigma}(x)=\pi_{\sigma}(r(x))\) для всех \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\). Таким образом, применяя (33), можно заменить \(x\) на \(r(x)\) без изменения обеих сторон уравнения. Следовательно, мы можем предположить, что \(x=\tilde{\sigma}(z)\) для некоторого \(z\in{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). Тогда \(\pi_{\sigma}(x)\) представляет собой просто умножение на \(z\). Имеется по (35) \[r\circ\tilde{\rho}_{n}(x)=r\circ\tilde{\rho}_{n}(\tilde{\sigma}(z))=\tilde{ \sigma}\circ V_{n}(z).\] \[\ r\circ\tilde{\rho}_{n}(x)=r\circ\tilde{\rho}_{n}(\tilde{\sigma}(z))=\tilde{ \sigma}\circ V_{n}(z).\] \[\ r\circ\tilde{\rho}_{n}(x)=r\circ\tilde{\rho}_{n}(\tilde{\sigma}(z))=\tilde{ \sigma}\circ V_{n}(z).\] \[\ r\circ\tilde{\rho}_{n}(x)=r\circ\tilde{\rho}_{n}(\tilde{\sigma}(z))=\tilde{ \sigma}\circ V_{n}(z).\] Таким образом, \(\pi_{\sigma}(\tilde{\rho}_{n}(x))\) - это умножение на \(V_{n}(z)\), и (38) следует от \[V_{n}(zF_{n}(\xi))=V_{n}(z)\xi\,,\quad~{}\forall\xi\in{\mathbb{W}}_{0}(\bar{ \mathbb{F}}_{p})\] can be translated to Russian as: \[V_{n}(zF_{n}(\xi))=V_{n}(z)\xi\,,\quad~{}\forall\xi\in{\mathbb{W}}_{0}(\bar{ \mathbb{F}}_{p})\] которое является утверждением (2) Предложения 2.2. Проверим другие два соотношения (21). Второе соотношение означает \[F_{n}\pi_{\sigma}(x)=\pi_{\sigma}(\sigma_{n}(x))F_{n}\] \[F_{n}\pi_{\sigma}(x)=\pi_{\sigma}(\sigma_{n}(x))F_{n}\] и так как \(r\circ\sigma_{n}=\sigma_{n}\circ r\), мы можем предположить, что \(x=\tilde{\sigma}(z)\), как и раньше, для некоторого \(z\in{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\). Тогда \(\pi_{\sigma}(x)\) является умножением на \(z\), и, согласно (35), \(\pi_{\sigma}(\sigma_{n}(x))\) является умножением на \(F_{n}(z)\). Требуемое равенство следует из того, что \(F_{n}\) является мультипликативной. Последнее соотношение из (21) означает \[\pi_{\sigma}(x)V_{n}=V_{n}\pi_{\sigma}(\sigma_{n}(x))\] will be translated to Russian as: \[\pi_{\sigma}(x)V_{n}=V_{n}\pi_{\sigma}(\sigma_{n}(x))\] и предполагая, что \(x=\tilde{\sigma}(z)\), это упрощается до \[\begin{aligned}zV_{n}(\xi)=V_{n}(F_{n}(z)\xi)\,,\quad~{}\forall\xi\in{\mathbb{W}}_{0}(\bar{ \mathbb{F}}_{p})\end{aligned}\] что, в свою очередь, следует из утверждения (2) Предложения 2.2. ∎ ## 5. Функтор векторов Витта и частичные частки В данном разделе мы предоставляем краткий обзор по строительству универсальной схемы Витта в форме, которая наиболее подходит для применений, содержащихся в данной статье. Для получения более подробной информации мы ссылаемся на [39, 28, 6, 22, 3, 33, 24]. Во второй части раздела мы связываем универсальное кольцо \({\mathbb{W}}_{0}(A)\) с \({\mathbb{W}}(A)\). Построение кольца больших векторов Витта (или обобщенных векторов Витта) описывается ковариантным эндофунктором \({\mathbb{W}}:\mathfrak{Ring}\to\mathfrak{Ring}\) в категории коммутативных колец (с единицей). Для \(A\in{\rm obj}(\mathfrak{Ring})\), и в качестве функтора в категорию множеств, определяется \[\mathbb{W}(A)=A^{\mathbb{N}}=\{(x_{1},x_{2},x_{3},\ldots)|x_{i}\in A\}.\] \[\mathbb{W}(A)=A^{\mathbb{N}}=\{(x_{1},x_{2},x_{3},\ldots)|x_{i}\in A\}.\] К набору обрезания \(N\subseteq{\mathbb{N}}\) (_т.е._ подмножество \({\mathbb{N}}\), которое содержит каждый положительный делитель каждого из своих элементов), ассоциируется обрезающий функтор \[\mathbb{W}_{N}:\mathfrak{Ring}\to\mathfrak{Sets},\qquad\mathbb{W}_{N}(A)=A ^{N}.\] Как функтор категории множеств, \({\mathbb{W}}_{N}\) лево представлен полиномиальным кольцом \(R_{N}={\mathbb{Z}}[x_{n}|n\in N]\). Отсюда следует, что большой функтор Витта \({\mathbb{W}}={\mathbb{W}}_{\mathbb{N}}\) лево представлен симметричной алгеброй \({\rm Symm}={\mathbb{Z}}[x_{1},x_{2},x_{3},\ldots]\) \[{\mathbb{W}}(A)={\mbox{Hom}}_{\mathfrak{Ring}}({\rm Symm},A)\qquad\forall A\in {\rm obj}(\mathfrak{Ring}).\] (39) \[{\mathbb{W}}(A)={\mbox{Гом}}_{\mathfrak{Ring}}({\rm Сим},A)\qquad\forall A\in {\rm obj}(\mathfrak{Ring}).\] (39) Как эндофунктор в категории коммутативных колец \({\mathbb{W}}_{N}:\mathfrak{Ring}\to\mathfrak{Ring}\) он _единственным образом_ определяется требованием, чтобы для любого коммутативного кольца \(A\) и для любого \(n\in N\) следующее отображение, называемое \(n\)-ым призрачным компонентом, было гомоморфизмом колец \[\text{{gh}}_{n}:{\mathbb{W}}_{N}(A)\to A,\quad \text{{gh}}_{n}(x)=\sum_{d|n}dx_{d}^{n/d}.\] (40) Для переменной \(t\), функториальное взаимно однозначное соответствие множеств \[\varphi_{A}:{\mathbb{W}}(A)\to\Lambda(A)=1+tA[[t]],\qquad x=(x_{n})_{n\in{ \mathbb{N}}}\mapsto f_{x}(t)=\prod_{n\in{\mathbb{N}}}(1-x_{n}t^{n})^{-1}\] (41) \[\varphi_{A}:{\mathbb{W}}(A)\to\Lambda(A)=1+tA[[t]],\qquad x=(x_{n})_{n\in{ \mathbb{N}}}\mapsto f_{x}(t)=\prod_{n\in{\mathbb{N}}}(1-x_{n}t^{n})^{-1}\] (41) переносит кольцевую структуру из \({\mathbb{W}}(A)\) в мультипликативную абелеву группу \(\Lambda(A)\) степенных рядов над \(A\) с постоянным членом \(1\), с помощью обычного умножения степенных рядов (степенной ряд \(1\) действует как единичный элемент). Другими словами, имеется \[\varphi_{A}(x+y)=\varphi_{A}(x)\varphi_{A}(y)\qquad\forall x,y\in{\mathbb{W}}( A).\] Для более ясного описания соответствующего продукта \(\star\) на \(\Lambda(A)\) вводятся сначала \(n\)-призраковые компоненты \(w_{n}:\Lambda(A)\rightarrow A\), \(n\in{\mathbb{N}}\), которые определяются формулой \[w(f)=w(1+a_{1}t+a_{2}t^{2}+a_{3}t^{3}+\cdots)=w_{1}t+w_{2}t^{2}+\cdots=t\frac{ d}{dt}(\log(f(t))).\] Перевод: \[w(f)=w(1+a_{1}t+a_{2}t^{2}+a_{3}t^{3}+\cdots)=w_{1}t+w_{2}t^{2}+\cdots=t\frac{ d}{dt}(\log(f(t))).\] Например, первые три компоненты духов даны универсальными формулами \[w_{1}(f)=a_{1},\quad w_{2}(f)=-a_{1}^{2}+2a_{2},\quad w_{3}(f)=a_{1}^{3}-3a_{1 }a_{2}+3a_{3}.\]is translated to: \[w_{1}(f)=a_{1},\quad w_{2}(f)=-a_{1}^{2}+2a_{2},\quad w_{3}(f)=a_{1}^{3}-3a_{1 }a_{2}+3a_{3}.\] Для произведений вида \(\prod_{k=1}^{m}(1-\xi_{k}t)^{-1}=1+a_{1}t+a_{2}t^{2}+\cdots=f(t)\) это означает, что \[ w_{1}t+w_{2}t^{2}+w_{3}t^{3}+\cdots =t\frac{d}{dt}(\log(f(t)))=t\frac{d}{dt}\sum_{k=1}^{m}\log((1-\xi _{k}t)^{-1})= \] \[ =\sum_{i=1}^{\infty}(\xi_{1}^{i}+\xi_{2}^{i}+\cdots+\xi_{m}^{i})t ^{i}=\sum_{i=1}^{\infty}p_{i}(\xi)t^{i}. \] Таким образом, "призрачные компоненты" задаются степенными суммами в \(\xi_{k}\). Затем, произведение \(\star\) на \(\Lambda(A)\) _единственным образом_ определяется требованием, чтобы эти "призрачные компоненты" были (функториальными) гомоморфизмами колец. Фактически, дистрибутивность и функториальность вместе заставляют умножение степенных рядов в \(\Lambda(A)\) быть выраженным следующим правилом \[\displaystyle f(t)=\prod_{i}(1-\xi_{i}t)^{-1},\quad g(t)=\prod_{i}(1-\eta_{i}t)^{-1},\quad \Rightarrow\quad(f\star g)(t)=\prod_{i,j}(1-\xi_{i}\eta_{j}t)^{-1}\] (42) где \[t\frac{d}{dt}(\log(\prod_{i,j}(1-\xi_{i}\eta_{j}t)^{-1}))=\sum_{n=1}^{\infty}p _{n}(\xi)p_{n}(\eta)t^{n}.\] \[t \frac{d}{dt} (\log(\prod_{i, j}(1 - \xi_{i}\eta_{j}t)^{-1})) = \sum_{n=1}^{\infty} p_n(\xi) p_n(\eta) t^n.\] Следовательно, умножение согласно (42) переводится в поэлементное умножение для компонент призраков на \(\Lambda(A)\). Это выражается явными полиномами с целочисленными коэффициентами формы \[ (1+\sum a_{n}t^{n})\star(1+\sum b_{n}t^{n})=1+a_{1}b_{1}t+(a_{1}^{2}b_{1} ^{2}-a_{2}b_{1}^{2}-a_{1}^{2}b_{2}+2a_{2}b_{2})t^{2}+\\ +(a_{1}^{3}b_{1}^{3}-2a_{1}a_{2}b_{1}^{3}+a_{3}b_{1}^{3}-2a_{1}^{3}b_{1}b_{2}+ 5a_{1}a_{2}b_{1}b_{2}-3a_{3}b_{1}b_{2}+a_{1}^{3}b_{3}-3a_{1}a_{2}b_{3}+3a_{3}b _{3})t^{3}+\cdots \] Компоненты-призраки \(gh_{n}(x)\) Виттового вектора \(x=(x_{1},x_{2},x_{3},\ldots)\in{\mathbb{W}}(A)\) становятся компонентами-призраками \(\varphi_{A}(x)\), _т.е._ \[gh_{n}:{\mathbb{W}}(A)\to A,\quad gh_{n}(x)=w_{n}(\varphi_{A}(x)).\] (43) \[\text{``}gh_{n}:{\mathbb{W}}(A)\to A,\quad gh_{n}(x)=w_{n}(\varphi_{A}(x)).\text{''} (43)\] Таким образом, биекция \(\varphi_{A}:{\mathbb{W}}(A)\to\Lambda(A)\) становится изоморфизмом колец. Обратите внимание, что гомоморфизм абелевых групп \(L:{\mathbb{W}}_{0}(A)\to\Lambda(A)\) из (8) сохраняет произведение, _т.е._ \[L((E,f)\otimes(F,g))=L((E,f))\star L((F,g))\] (44) \[L((E,f)\otimes(F,g))=L((E,f))\star L((F,g))\] (44) так чтобы оно определяло инъективный гомоморфизм колец. Два вектора Уитта \(x, y \in {\mathbb{W}}(A)\) складываются и умножаются с помощью универсальных полиномов с целочисленными коэффициентами \[x+_{{\mathbb{W}}}y=(\mu_{S,1}(x,y),\mu_{S,2}(x,y),\ldots),\quad x\times_{{ \mathbb{W}}}y=(\mu_{P,1}(x,y),\mu_{P,2}(x,y),\ldots).\] Многочлены \(\mu_{S,i}, \mu_{P,j}\) рекурсивно вычисляются с использованием фантомных компонентов по следующим формулам: \[gh_{n}(\mu_{S,1}(x,y),\mu_{S,2}(x,y),\ldots)=gh_{n}(x)+gh_{n}(y),\] would be translated to: \[gh_{n}(\mu_{S,1}(x,y),\mu_{S,2}(x,y),\ldots)=gh_{n}(x)+gh_{n}(y),\] \[\gh_{n}(\mu_{P,1}(x,y),\mu_{P,2}(x,y),\ldots)=gh_{n}(x)gh_{n}(y).\] Обратите внимание, что полиномы \(gh_{n}(x)\) зависят только от \(x_{d}\) для \(d\) - делителя \(n\), поэтому \(n\)-тые полиномы сложения и умножения \(\mu_{S,n}\), \(\mu_{P,n}\) - это полиномы, которые включают только \(x_{d}\) и \(y_{d}\) с делителями \(n\). Таким образом, для множества обрезания \(N\subseteq{\mathbb{N}}\), кольцо полиномов \(R_{N}={\mathbb{Z}}[x_{n}|n\in N]\) является подалгеброй Хопфа и подкольцевым объектом \({\rm Symm}\), это означает, что оно определяет функтор отношения, который совпадает с \({\mathbb{W}}_{N}\). Этот результат относится в частности к множеству обрезания \(N=\{p^{n}\mid n\geq 0\}\), где \(p\) - простое число. Таким образом, p-адические числа Витт \({\mathbb{W}}_{p^{\infty}}(A)\) могут быть истолкованы как функториальное отношение больших чисел Витт (аналогично, получается \({\mathbb{W}}_{p^{n}}(A)\) как p-адические числа Витт длины \(n+1\)). Представитель Тейхмюллера является мультипликативным отображением, которое определяет сечение для призракового отображения \(gh_{1}\). Если \(N\subset{\mathbb{N}}\) - это множество усечения, то представитель Тейхмюллера определяется как \[[\cdot]_{N}:A\to{\mathbb{W}}_{N}(A),\quad a\mapsto[a]_{N}=([a]_{N})_{n\in N}, \quad[a]_{N,n}=\begin{cases}a&\text{если $n=1$},\\ 0&\text{если $n>1$}.\end{cases}\] Одно имеет \(gh_{n}([a]_{N})=a^{n}\) для всех \(n\in N\). На функториальном кольце \({\mathbb{W}}(A)\) можно ввести несколько функториальных операций, которые производятся (большим количеством) кольцевых эндоморфизмов \({\rm Symm}\) и путем применения свойства представимости (39). Например, эндоморфизмы Вершабунг (сдвиг) аддитивного функтора на \({\mathbb{W}}\) и его квофиенты возникают из кольцевого эндоморфизма. \[{\bf V}_{n}:{\rm Symm}\to{\rm Symm}\,,\ \ x_{i}\mapsto\begin{cases}x_{i/n}& \text{если $i$ делится на $n$}\\ 0&\text{в противном случае}\end{cases}\] который соответствует отображению \(f(t)\mapsto f(t^{n})\) в \(\Lambda(A)\). Для \(N\subset{\mathbb{N}}\) - множества усечения, сдвиг является аддитивным отображением, заданным \[V_{n}:{\mathbb{W}}_{N/n}(A)\to{\mathbb{W}}_{N}(A),\quad V_{n}((a_{d}|d\in N/n) )=(a_{m}^{\prime}|m\in N);~{}a_{m}^{\prime}=\begin{cases}a_{d}&\text{если $m=nd$ }\\ 0&\text{иначе}\end{cases}\] где \(N/n=\{d\in{\mathbb{N}}|nd\in N\}\). Это означает, что составной с компонентами призрака дано \[gh_{m}V_{n}=\begin{cases}ngh_{m/n}&\text{если $n$ делит $m$}\\ 0&\text{в противном случае.}\end{cases}\] (45) n-ый Фробениус является (единственным) естественным гомоморфизмом колец. \[F_{n}:{\mathbb{W}}_{N}(A)\to{\mathbb{W}}_{N/n}(A)\] can be translated to Russian as: \[ F_{n}:{\mathbb{W}}_{N}(A)\rightarrow{\mathbb{W}}_{N/n}(A) \] который определен на экспонентных компонентах по формуле \(gh_{r}F_{n}=gh_{rn}\). Таким образом, по определению \(n\)-е отображение Фробениуса заставляет следующую диаграмму коммутировать \[\begin{CD}\mathbb{W}_{N}(A)@>{gh}>{}>A^{N}\\ @V{F_{n}}VV@VV{F_{n}^{gh}}V\\ \mathbb{W}_{N/n}(A)@>{gh}>{}>A^{N/n}\end{CD}\] где \(F_{n}^{gh}\) превращает последовательность \((a_{m}|m\in N)\) в последовательность, у которой d-й компонент \(a_{dn}\). На уровне компонент \(x_{j}\) виттова вектора \(x\in{\mathbb{W}}_{N}(A)\), Фробениус \(F_{n}\) задается многочленами с целочисленными коэффициентами. Например, следующие являются первыми \(5\) компонентами \(F_{3}(x)\). \[F_{3}(x)_{1} = x_{1}^{3}+3x_{3}\] \[F_{3}(x)_{2} = x_{2}^{3}-3x_{1}^{3}x_{3}-3x_{3}^{2}+3x_{6}\] \[F_{3}(x)_{3} = -3x_{1}^{6}x_{3}-9x_{1}^{3}x_{3}^{2}-8x_{3}^{3}+3x_{9}\] \[F_{3}(x)_{4} = -3x_{1}^{9}x_{3}+3x_{1}^{3}x_{2}^{3}x_{3}-18x_{1}^{6}x_{3}^{2}+3x _{2}^{3}x_{3}^{2}-36x_{1}^{3}x_{3}^{3}\] \[-24x_{3}^{4}+x_{4}^{3}-3x_{2}^{3}x_{6}+9x_{1}^{3}x_{3}x_{6}+9x_{3 }^{2}x_{6}-3x_{6}^{2}+3x_{12}\] \[F_{3}(x)_{5} = -3x_{1}^{12}x_{3}-18x_{1}^{9}x_{3}^{2}-54x_{1}^{6}x_{3}^{3}-81x_{ 1}^{3}x_{3}^{4}-48x_{3}^{5}+x_{5}^{3}+3x_{15}.\] Обратите внимание, что при \(p\) является рациональным простым числом, имеет место (_см._[30] Предложение 5.12) \[F_{p}(x)_{m}\equiv x_{m}^{p}~{}({\rm mod}~{}pA).\] (46) \[F_{p}(x)_{m}\equiv x_{m}^{p}~{}(\mod~{}pA).\] (46) Однако, (_см._[30], Предложение 5.9) имеется: \[V_{nm}=V_{n}\circ V_{m}=V_{m}\circ V_{n}\,,\ \ F_{nm}=F_{n}\circ F_{m}=F_{m} \circ F_{n}\] (47) \[V_{nm}=V_{n}\circ V_{m}=V_{m}\circ V_{n}\,,\ \ F_{nm}=F_{n}\circ F_{m}=F_{m} \circ F_{n}\] (47) где для отображений \(F_{n}\) предполагается, что \(nN\subset N\) и \(mN\subset N\). Предложение 2.2 не меняется (_см._ [30] Предложение 5.10). **Утверждение 5.1**. _Пусть \(N\subset{\mathbb{N}}\) - множество обрезания, и \(n\in N\) такое, что \(nN\subset N\). Пусть \(A\) - коммутативное кольцо и \(x,y\in{\mathbb{W}}_{N}(A)\). Тогда_ \((1)\)_\(F_{n}\circ V_{n}(x)=nx\). \((1)\)_\(F_{n}\circ V_{n}(x)=nx\). \((2)\)_\(V_{n}(F_{n}(x)y)=xV_{n}(y)\)._ Если \(m\) взаимно просто с \(n\), то выполняется \(V_{m}\circ F_{n}=F_{n}\circ V_{m}\). \((4)\) _У нас есть \(V_{n}(x)V_{n}(y)=nV_{n}(xy)\)_. Доказательство: Мы ссылаемся на предложение 5.10 из [30]. Утверждение (4) немного отличается от этой ссылки, его можно проверить непосредственно, используя предложение 2.2. Оно подразумевает, что когда \(n\) обратимо в \({\mathbb{W}}_{N}(A)\), то \(\frac{1}{n}V_{n}\) определяет кольцевой эндоморфизм. ∎ Важно видеть, как описание универсального кольца \({\mathbb{W}}_{0}(A)\) соответствует определению \({\mathbb{W}}(A)\). Существует канонический мономорфизм колец \({\mathbb{W}}_{0}(A)\hookrightarrow{\mathbb{W}}(A)\), который задается как композиция инъективного гомоморфизма колец \(L:{\mathbb{W}}_{0}(A)\to\Lambda(A)\), как в (8), и изоморфизма колец \(\varphi_{A}^{-1}:\Lambda(A)\stackrel{{\sim}}{{\to}}{\mathbb{W}}(A)\) (_см._ (41)). \[\mathbb{W}_{0}(A)\to\Lambda(A)\simeq\mathbb{W}(A),\qquad(E,f)\mapsto\det(1 -tM(f))^{-1}.\] (48) В случае \(A=\bar{\mathbb{F}}_{p}\) характеристический полином \(\det(1-tM(f))=\det(1-tf)\) факторизуется в произведение термов \((1-t\alpha_{j})\) степени один, где \(\alpha_{j}\in\bar{\mathbb{F}}_{p}\) являются собственными значениями \(f\) (_сравните (13)). **Лемма 5.2****.**: _Пусть \([\cdot]:\bar{\mathbb{F}}_{p}\to{\mathbb{W}}(\bar{\mathbb{F}}_{p}),~{}x\mapsto \tau(x):=[x]\) будет подъемом Тайхмюллера, а \(\delta:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\to{\mathbb{Z}}[\bar{\mathbb{F}}_ {p}^{\times}]\) будет изоморфизмом (12). Тогда каноническое отображение (48) задается явно как_ \[j:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\to{\mathbb{W}}(\bar{\mathbb{F}}_{p}), \quad j\circ\delta^{-1}:{\mathbb{Z}}[\bar{\mathbb{F}}_{p}^{\times}]\ni\sum n_{ j}\alpha_{j}\mapsto\sum n_{j}\tau(\alpha_{j})\in{\mathbb{W}}(\bar{\mathbb{F}}_ {p}).\] (49) \[j:{\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\to{\mathbb{W}}(\bar{\mathbb{F}}_{p}), \quad j\circ\delta^{-1}:{\mathbb{Z}}[\bar{\mathbb{F}}_{p}^{\times}]\ni\sum n_{ j}\alpha_{j}\mapsto\sum n_{j}\tau(\alpha_{j})\in{\mathbb{W}}(\bar{\mathbb{F}}_ {p}).\] (49) Эта лемма вместе с Теоремой 2.1 показывает, что подкольцо \( {\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\subset{\mathbb{W}}(\bar{\mathbb{F}}_{p}) \) представляет собой групповое кольцо \( {\mathbb{Z}}[\bar{\mathbb{F}}_{p}^{\times}] \) и свободно порождается над \( {\mathbb{Z}} \) лифтами Тейхмюллера. ## 6. \(p\)-адическое представление \(\pi_{\sigma}\) системы BC В этом разделе мы реализуем результаты [6, 33, 3], чтобы описать кольцо \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\), затем, используя вложение с плотным образом \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\hookrightarrow{\mathbb{W}}(\bar{\mathbb {F}}_{p})\), мы расширим представление \(\pi_{\sigma}\) группы \({\mathcal{H}}_{\mathbb{Z}}\) на \({\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p})\) (Теорема 4.5) до представления интегральной BC-системы на \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). Такое представление является \(p\)-адическим аналогом неразложимого комплексного представления (86). Начнем с напоминания определения изоморфизма. \[\mathbb{W}(\bar{\mathbb{F}}_{p})\simeq \mathbb{W}_{p^{\infty}}(\bar{\mathbb{F}}_{p})^{I(p)}\] (50) где \(I(p)\subset{\mathbb{N}}\) - множество положительных целых чисел, взаимно простых с \(p\), а \(p^{\infty}\) - множество целых степеней \(p\). На концептуальном уровне, данная изоморфность является особым случаем общего изоморфизма функторов, справедливого для любого коммутативного кольца \(A\) с единицей ([3] Теорема 1). \[\mathbb{W}(A)=\mathbb{W}_{I(p)}(\mathbb{W}_{p^{\infty}}(A)).\] (51) Когда \(A\) является \({\mathbb{F}}_{p}\)-алгеброй, каждый элемент \(\text{I}(p)\) обратим в \(B={\mathbb{W}}_{p^{\infty}}(A)\), следовательно, получается канонический изоморфизм \({\mathbb{W}}_{\text{I}(p)}(B)\simeq B^{\text{I}(p)}\), который определен в терминах спектральных компонент. Пусть \({\mathbb{Z}}_{(p)}\) - это кольцо \({\mathbb{Z}}\), локализованное в простом идеале \(p{\mathbb{Z}}\), так что каждый элемент \(\text{I}(p)\) обратим в \({\mathbb{Z}}_{(p)}\). Центральная роль в кольце \(\Lambda({\mathbb{Z}}_{(p)})\) играется артин-хассовым экспонентом, которая является степенным рядом. \[\displaystyle E_{p}(t)={\rm hexp}(t)={\rm exp}(t+\frac{t^{p}}{p}+\frac{t^{p^{2}}}{p^{2}}+ \cdots)\in\Lambda({\mathbb{Z}}_{(p)}).\] (52) Следующие свойства хорошо известны (_см._[3, 33]) **Предложение 6.1**: \((1)\)_\(E_{p}(t)\) является идемпотентом \(\Lambda({\mathbb{Z}}_{(p)})\)._ \((2)\) _Для \(n\in I(p)\), ряд \(E_{p}(n)(t):=\frac{1}{n}V_{n}(E_{p})(t)\in\Lambda({\mathbb{Z}}_{(p)})\) определяется как идемпотент. При изменении \(n\) в \(I(p)\), \(E_{p}(n)\) формируют разбиение единицы с помощью идемпотентов._ \((3)\) _Для \(n\notin p^{\mathbb{N}}\), \(F_{n}(E_{p})(t)=1(=0_{\Lambda})\) и \(F_{p^{k}}(E_{p})(t)=E_{p}(t)\), \(\forall k\in{\mathbb{N}}\)._ Для проверки \((1)\) непосредственно показывается, что существует единственная последовательность \((x_{n})_{n\in{\mathbb{N}}}\in{\mathbb{W}}({\mathbb{Z}}_{(p)})\) такая, что \(\bullet\)\(x_{1}=1\) \(\bullet\) \(x_{p^k} = 0\) для всех \(k > 0\) \(\bullet\) \(F_{m}(x)_{p^{k}}=0\) для всех \(m\in I(p)\) и \(k\geq 0\). Это следует из того, что коэффициент \(x_{mp^{k}}\) в \(F_{m}(x)_{p^{k}}\) равен \(m \in I(p)\), который обратим в \({\mathbb{Z}}_{(p)}\), так что \(x_{n}\) определяется индуктивно. Затем проверяется, что «призрачные» компоненты \((x_{n})_{n\in{\mathbb{N}}}\in{\mathbb{W}}({\mathbb{Z}}_{(p)})\) совпадают с компонентами \(E_{p}(t)\), _т.е._ \(gh_{n}(x)\) равно 1, если \(n\in p^{\mathbb{N}}\), и нулю в противном случае. Обратите внимание, что любое \(n\in I(p)\) является обратимым в \(\Lambda({\mathbb{Z}}_{(p)})\). Деление на \(n\) соответствует извлечению \(n\)-го корня из степенного ряда \(f(t)=1+g(t)\). Формально это задается биномиальной формулой. \[ f^{\frac{1}{n}}=(1+g)^{\frac{1}{n}}=1+\frac{1}{n}g+\ldots+\frac{\frac{1}{n}( \frac{1}{n}-1)\cdots(\frac{1}{n}-k+1)}{k!}g^{k}+\ldots\] (53) \] \[f^{\frac{1}{n}}=(1+g)^{\frac{1}{n}}=1+\frac{1}{n}g+\ldots+\frac{\frac{1}{n}( \frac{1}{n}-1)\cdots(\frac{1}{n}-k+1)}{k!}g^{k}+\ldots\] (53) \(p\)-адическая оценка рационального коэффициента \(g^{k}\) положительна, потому что \(\frac{1}{n}\in{\mathbb{Z}}_{p}\), следовательно, этот коэффициент может быть произвольно приближен биномиальным коэффициентом. Из Предложения 2.2, \((4)\) следует, что \(\frac{1}{n}V_{n}\) является эндоморфизмом \(\Lambda(\bar{\mathbb{F}}_{p})\) и также правым обратным элементом \(F_{n}\). Один легко выводит из [6, 3, 33] следующий результат **Утверждение 6.2****.**: _Пусть \(A\) будет алгеброй \({\mathbb{F}}_{p}\)._ \((a)\) _Карта_ \[\psi_{A}:{\mathbb{W}}_{p^{\infty}}(A)\to\Lambda(A)_{E_{p}},\quad x=(x_{p^{n}}) _{n\in{\mathbb{N}}},\quad\psi_{A}(x)(t):=h_{x}(t)=\prod_{\mathbb{N}}E_{p}(x_{p ^{n}}t^{p^{n}})\] (54) \[\psi_{A}:{\mathbb{W}}_{p^{\infty}}(A)\to\Lambda(A)_{E_{p}},\quad x=(x_{p^{n}}) _{n\in{\mathbb{N}}},\quad\psi_{A}(x)(t):=h_{x}(t)=\prod_{\mathbb{N}}E_{p}(x_{p ^{n}}t^{p^{n}})\] (54) _является изоморфизмом на сокращенное кольцо \(\Lambda(A)_{E_{p}}=\{x\in\Lambda(A)\mid x\star E_{p}=x\}\)._ \((b)\) _Для \(n\in I(p)\), композиция \(\psi_{A}^{-1}\circ F_{n}\) является изоморфизмом между уменьшенной алгеброй \(\Lambda(A)_{E_{p}(n)}\) и \({\mathbb{W}}_{p^{\infty}}(A)\)._ \((с)\) _Составной_ \[\theta_{A}(x)=(\theta_{A}(x))_{n}=\psi_{A}^{-1}\circ F_{n}(x\star E_{p}(n)),\ \ n\in I(p),~{}x\in\Lambda(A)\] (55) \[\theta_{A}(x)=(\theta_{A}(x))_{n}=\psi_{A}^{-1}\circ F_{n}(x\star E_{p}(n)),\ \ n\in I(p),~{}x\in\Lambda(A)\] (55) _является каноническим изоморфизмом \(\theta_{A}:\Lambda(A)\to{\mathbb{W}}_{p^{\infty}}(A)^{I(p)}={\mathbb{W}}(A)\)._ \((d)\) _Составная изоморфизм \(\Theta_{A}:=\theta_{A}\circ\varphi_{A}:{\mathbb{W}}(A)\to{\mathbb{W}}_{p^{ \infty}}(A)^{I(p)}\) явно задается на компонентах следующим образом_ \[(\Theta_{A}(x)_{n})_{p^{k}}=F_{n}(x)_{p^{k}}\,,\quad~{}\forall x\in{\mathbb{W} }(A)\,,\quad~{}\forall n\in I(p).\] (56) \[(\Theta_{A}(x)_{n})_{p^{k}}=F_{n}(x)_{p^{k}}\,,\quad~{}\text{для всех } x\in{\mathbb{W} }(A)\,,\quad~{}\text{для всех } n\in I(p).\] (56) Доказательство: Первые три утверждения следуют из [6] §3.b, [3], теоремы 1 и предложения 1, [33], теоремы 9.15. Мы докажем \((d)\). Поскольку Фробениус \(F_{n}\) является эндоморфизмом, и \(F_{n}(x\star E_{p}(n))=F_{n}(x)\star E_{p}\), можно переписать (55) как \[(\theta_{A}(x))_{n}=\psi_{A}^{-1}(E_{p}\star F_{n}(x))\,,\quad~{}\forall n\in I (p).\] (57) \[(\theta_{A}(x))_{n}=\psi_{А}^{-1}(E_{p}\star F_{n}(x))\,,\quad~{}\forall n\in I (p).\] (57) Таким образом, чтобы показать (56), достаточно доказать это для \(n=1\). Необходимо проверить, что для всех \(x\in{\mathbb{W}}(A)\) выполняется. \[E_{p}\star\varphi_{A}(x)=\prod_{\mathbb{N}}E_{p}(x_{p^{n}}t^{p^{n}}).\] \[E_{p} \star \varphi_{A}(x) = \prod_{\mathbb{N}}E_{p}(x_{p^{n}}t^{p^{n}}).\] Действительно, это следует из дистрибутивности и тождества \[\ E_{p}\star(1-xt^{n})^{-1}=\left\{\begin{array}[]{ll}1&\hbox{если}\ n\notin p^{ \mathbb{N}}\\ E_{p}(xt^{p^{k}})&\hbox{если}\ n=p^{k}.\end{array}\right.\] Вышеприведенное тождество можно проверить, зная, что \((1-xt^{n})^{-1}=V_{n}(\tau(x))\), и применяя равенство \[E_{p}\star(1-xt^{n})^{-1}=E_{p}\star V_{n}(\tau(x))=V_{n}(F_{n}(E_{p})\star \tau(x))\] translates to: \[E_{p}\star(1-xt^{n})^{-1}=E_{p}\star V_{n}(\tau(x))=V_{n}(F_{n}(E_{p})\star \tau(x))\] вместе с Предложением 6.1\((3)\) и равенством \[\tau(y)\star f(t)=(1-yt)^{-1}\star f(t)=f(yt)\] \[\tau(y)\star f(t) = (1-yt)^{-1}\star f(t) = f(yt)\] которое справедливо для любого элемента \(f(t)\in\Lambda(A)\). В частности, для подъема Тейхмюллера \(\tau(y)=[y]\) элемента \(y\in A\) получается \[\theta_{А}(\tau(y))_{n}=\tau(y^{n})\,,\quad~{}\forall n\in I(p)\] (58) где справа стоит \(\tau\), обозначающий исходный подъем Тайхмюллера \(\tau:A\to{\mathbb{W}}_{p^{\infty}}(A)\). Действительно, \(F_{n}(\tau(y))=\tau(y^{n})\). ∎ **Следствие 6.3**. Пусть \(A\) является \({\mathbb{F}}_{p}\)-алгеброй. Тогда общие неподвижные точки эндоморфизмов \(F_{n}:{\mathbb{W}}(A)\to{\mathbb{W}}(A)\) для \(n\in I(p)\) являются элементами формы. \[L(\lambda)=\sum_{m\in I(p)}\frac{1}{m}V_{m}(E_{p}\star\lambda)\,,\ \ \lambda \in{\mathbb{W}}_{p^{\infty}}(A).\] (59) \[L(\lambda)=\sum_{m\in I(p)}\frac{1}{m}V_{m}(E_{p}\star\lambda)\,,\ \ \lambda \in{\mathbb{W}}_{p^{\infty}}(A).\] (59) _Однако также имеется_ \[\varphi_{A}(L(\lambda))=\prod_{n\in I(p)}h_{\lambda}(t^{n})^{\frac{1}{n}}.\] would be translated to Russian as: \[\varphi_{A}(L(\lambda))=\prod_{n\in I(p)}h_{\lambda}(t^{n})^{\frac{1}{n}}.\] Доказательство: Пусть \(x\in{\mathbb{W}}(A)\) с \(F_{n}(x)=x\) для всех \(n\in I(p)\). Тогда из (56) и (55) следует, что все компоненты \((\theta_{A}(x))_{n}\) равны, так что для некоторого \(\lambda\in{\mathbb{W}}_{p^{\infty}}(A)\) имеем \[E_{p}(n)\star x=\frac{1}{n}V_{n}(E_{p}\star\lambda)\] и \(x\) имеет нужную форму. Обратно, согласно Предложению 6.1\((3)\), имеется \(F_{a}(E_{p})=0_{\Lambda}\) для всех \(a\in I(p),\,a\neq 1\). Таким образом, когда применяется \(F_{k}\) к \(\frac{1}{n}V_{n}(E_{p}\star\lambda)\), получается \(1(=0_{\Lambda})\) если только \(k|n\) с использованием Предложения 5.1\((2)\), \((3)\). Когда \(k|n\), получается \(\frac{1}{m}V_{m}(E_{p}\star\lambda)\), где \(m=n/k\). Таким образом, элементы формы (59) фиксированы при всех \(F_{k}\). ∎ Мы теперь применяем эти результаты к случаю \(A=\bar{\mathbb{F}}_{p}\). Мы идентифицируем \({\mathbb{W}}_{p^{\infty}}(\bar{\mathbb{F}}_{p})\) с подкольцом \({\mathbb{C}}_{p}\) (падическое завершение алгебраического замыкания \({\mathbb{Q}}_{p}\)). Пусть \(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}\subset{\mathbb{C}}_{p}\) будет завершением максимального нерамифицированного расширения \({\mathbb{Q}}_{p}\). Тогда известно, что \({\mathbb{W}}_{p^{\infty}}(\bar{\mathbb{F}}_{p})={\mathcal{O}}_{\widehat{{ \mathbb{Q}}_{p}^{\rm ur}}}\) является кольцом целых чисел \(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}\). C \(\Theta\) изоморфизмом (56), у нас есть \[\Theta:{\mathbb{W}}(\bar{\mathbb{F}}_{p})\stackrel{{\sim}}{{\to}}( {\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}})^{I(p)}\,,\ \ (\Theta(x)_{ n})_{p^{k}}=F_{n}(x)_{p^{k}},\quad\forall n\in I(p),~{}\forall x\in{\mathbb{W} }(\bar{\mathbb{F}}_{p}).\] (60) \[\Theta:{\mathbb{W}}(\bar{\mathbb{F}}_{p})\stackrel{{\sim}}{{\to}}( {\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}})^{I(p)}\,,\ \ (\Theta(x)_{ n})_{p^{k}}=F_{n}(x)_{p^{k}},\quad\forall n\in I(p),~{}\forall x\in{\mathbb{W} }(\bar{\mathbb{F}}_{p}).\] (60) Таким образом, \(\Theta\) делает \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\) модулем над \({\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\). Соответствует Фробениус-автоморфизму \(\bar{\mathbb{F}}_{p}\) , по функториальности, канонический автоморфизм \({\rm Fr}\) от \({\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\) , который расширяется до непрерывного автоморфизма. \[{\rm Fr}\in{\rm Aut}(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}).\] (61) can be translated to Russian as: \[\text{{Fr}}\in\text{{Aut}}(\widehat{{\mathbb{Q}}_{p}^{\text{{ur}}}}).\] (61) Мы теперь можем описать \(p\)-адические аналоги комплексных неразложимых представлений системы BC (_см._ (86)). Напомним, что \(X_{p}\) обозначает пространство всех инъективных гомоморфизмов групп \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to{\mathbb{C}}^{\times}\). Выбор \(\sigma\in X_{p}\) определяет вложение \(\rho:{\mathbb{Q}}^{\rm cyc,p}\to{\mathbb{C}}_{p}\) циклотомического поля, порожденного абстрактными корнями из единицы порядка, взаимно простого с \(p\), внутри \({\mathbb{C}}_{p}\). На следующем этапе мы будем использовать упрощенную нотацию \({\mathcal{O}}={\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\). Для \(m\in I(p)\) пусть \(\epsilon_{m}\) будет вектором в \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\) с только одной ненулевой компонентой: \(\epsilon_{m}(m)=1\). **Теорема 6.4**. Пусть \(\sigma\in X_{p}\). Представление \(\pi_{\sigma}\) такое же, как в Теореме 4.5, продолжается непрерывно до представления интегральной BC-алгебры \({\mathcal{H}}_{\mathbb{Z}}\) на \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). Для \(n\in I(p)\) и для \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), \(\pi_{\sigma}(\mu_{n})\), \(\pi_{\sigma}(x)\) и \(\pi_{\sigma}(\mu_{n}^{*})\) являются \({\mathcal{O}}\)-линейными операторами на \({\mathbb{W}}(\bar{\mathbb{F}}_{p})\). \[\pi_{\sigma}(\mu_{n})\epsilon_{m}=\epsilon_{nm},\ \ \ \ \pi_{ \sigma}(e(a/b)) \epsilon_{m}=\rho(\zeta_{a/b}^{m})\epsilon_{m}\,,\quad~{}\forall a \in{\mathbb{Z}},\ \forall b,m\in I(p)\] (62) \[\pi_{\sigma}(\mu_{n})\epsilon_{m}=\epsilon_{nm},\ \ \ \ \pi_{\sigma}(e(a/b)) \epsilon_{m}=\rho(\zeta_{a/b}^{m})\epsilon_{m}\,,\quad~{}\text{для всех } a \in{\mathbb{Z}},\ \text{для всех } b,m\in I(p)\] (62) \[\pi_{\sigma}(\mu_{n}^{*})\epsilon_{k}=\left\{\begin{array}[]{ll}0&\hbox{если}\,k \notin n{\mathbb{N}}\\ \epsilon_{k/n}&\hbox{если}\,k\in n{\mathbb{N}}\,.\end{array}\right.\] (63) _У нас есть \(\pi_{\sigma}(x)=\pi_{\sigma}(r(x))\) для всех \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) (\(r:{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{({\mathbb{Q}}/{ \mathbb{Z}})^{(p)}}]\) ретракция как в (28)) и_ \[\pi_{\sigma}(\mu_{p})={\rm Fr}^{-1},\quad\pi_{\sigma}(\mu_{p}^{*})={\rm Fr}\] (64) is translated as: \[\pi_{\sigma}(\mu_{p})={\rm Fr}^{-1},\quad\pi_{\sigma}(\mu_{p}^{*})={\rm Fr}\] (64) _где \({\rm Fr}\) - автоморфизм Фробениуса, действующий компонентно как антилинейный оператор._ Доказательство: Теоремы 4.5 и плотность \( {\mathbb{W}}_{0}(\bar{\mathbb{F}}_{p}) \) в \( {\mathbb{W}}(\bar{\mathbb{F}}_{p}) \) (_cf.__e.g._[23], 1.8) показывают, что \( \pi_{\sigma} \) продолжается непрерывно до представления целочисленной BC-алгебры \( {\mathcal{H}}_{\mathbb{Z}} \) на \( {\mathbb{W}}(\bar{\mathbb{F}}_{p}) \). В связи с обратимостью элементов \( n\in I(p) \) в \( {\mathbb{W}}(\bar{\mathbb{F}}_{p}) \), описание представления \( \pi_{\sigma} \) упрощается с использованием элементов \( \mu_{n}=\frac{1}{n}\tilde{\mu}_{n} \), чтобы подчеркнуть аналогию с комплексным случаем. Из следствия 6.3 следует, что подкольцо \( {\mathcal{O}} \) в \( {\mathbb{W}}(\bar{\mathbb{F}}_{p}) \) является неподвижным подкольцом для действия операторов \( F_{n} \), для всех \( n\in I(p) \). Для \( n\in I(p) \) операторы \( F_{n} \) являются \( {\mathcal{O}} \)-линейными, подобно \( V_{n} \) (_cf._ Предложение 2.2, \((2)\)), которые соответствуют \( \tilde{\mu}_{n} \) с помощью представления \( \pi_{\sigma} \). Таким образом, получаем первое равенство в (62). Операторы \( \pi_{\sigma}(e(a/b)) \) - это операторы умножения (_cf._ Следствие 2.4) на \( \tau(e(a/b)) \), поэтому они \( {\mathcal{O}} \)-линейны, и второе уравнение в (62) следует из (58). Применяя (37), получаем \( \pi_{\sigma}(\mu_{n}^{*})=F_{n} \) для всех \( n \). Взяв \( n=p \), получаем, что \( \pi_{\sigma}(\mu_{p}^{*})=F_{p} \), что совпадает с действием \( {\rm Fr} \) компонентно, как следует из коммутации \( F_{p}\circ\frac{1}{n}V_{n}=\frac{1}{n}V_{n}\circ F_{p} \) для \( n\in I(p) \) и (46). Поскольку \( \mu_{p}^{*}\mu_{p}=1 \) и \( {\rm Fr} \) обратим, получаем (64). ∎ **Определение 6.5**: _Обозначим через \({\mathcal{J}}_{p}\subset{\mathcal{H}}_{\mathbb{Z}}\) двусторонний идеал, порожденный элементами_ \ [1-e(p^{-k})\,,\quad~{}\forall k\in{\mathbb{N}}.\] (65) \[1-e(p^{-k})\,,\quad~{}\forall k\in{\mathbb{N}}.\] (65) **Утверждение 6.6.**: _У нас есть \({\mathcal{J}}_{p}={\rm Ker}\,\pi_{\sigma}\) (см. (62)) и пересечение \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\cap{\mathcal{J}}_{p}\) является идеалом \({\mathcal{J}}_{p}^{0}\) в \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), порожденным элементами, как в (65)._ _Последовательность коммутативных алгебр_ \[0\rightarrow{\mathcal{J}}_{p}^{0}\rightarrow{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\stackrel{{ r}}{{\longrightarrow}}{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{ (p)}}]\rightarrow 0\] (66) _это точно._ Доказательство .: Пусть \(r=id_{{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]}\otimes\epsilon:{ \mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\to{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{ Z}})^{(p)}}]\) будет отображением ретракции, введенным в (28). Согласно конструкции, имеем \[{ \mathcal{J}}_{p}^{0}={\rm Ker}(r). \] (67) Поскольку \(\pi_{\sigma}(e(a/b))\) зависит только от \(r(e(a/b))\), следует, что \({\mathcal{J}}_{p}\subset{\rm Ker}\,\pi_{\sigma}\). Известно (_см._[15], Лемма 4.8), что любой элемент алгебры \({\mathcal{H}}_{\mathbb{Z}}\) можно записать в виде конечной суммы мономов вида \[\sum_{\{a,b\}\in{\mathbb{N}}^{2}\atop(a,b)=1}\tilde{\mu}_{a}\,x_{\{a,b\}}\,\mu _{b}^{*},\qquad x_{\{a,b\}}\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}].\] (68) \[\sum_{{\{a,b\}\in{\mathbb{N}}^{2}\atop(a,b)=1}}\tilde{\mu}_{a}\,x_{\{a,b\}}\,\mu _{b}^{*},\qquad x_{\{a,b\}}\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}].\] (68) Мы доказываем, что для любой конечной суммы \(X\), как в (68), у нас есть \[\pi_{\sigma}(X)=0\implies x_{\{a,b\}}\in{\mathcal{J}}_{p}^{0}.\] (69) translates to: \[ \pi_{\sigma}(X)=0 \implies x_{\{a,b\}}\in{\mathcal{J}}_{p}^{0}. \] (69) Достаточно доказать, что \(r(x_{\{a,b\}})=0\), \(\forall a,b\in{\mathbb{N}}\), и так как \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) является свободным от кручения, достаточно показать, что \(ar(x_{\{a,b\}})=0\), \(\forall a,b\in{\mathbb{N}}\). Определим \(y:{\mathbb{Q}}_{+}^{*}\to{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\), \(y(\frac{a}{b}):=a\,r(x_{\{a,b\}})\), затем \(y\) имеет конечную поддержку. Для любого гомоморфизма группы \[\chi:{(\mathbb{Q}/\mathbb{Z})^{(p)}}\to\mathcal{O}^\times\] есть единственный гомоморфизм колец \(h_{\chi}\) с \[h_{\chi}:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathcal{O}}, \qquad h_{\chi}(e(\gamma))=\chi(\gamma)\,,\quad~{}\forall\gamma\in{({\mathbb{Q }}/{\mathbb{Z}})^{(p)}}.\] (70) \[h_{\chi}:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathcal{O}}, \qquad h_{\chi}(e(\gamma))=\chi(\gamma)\,,\quad~{}\forall\gamma\in{({\mathbb{Q }}/{\mathbb{Z}})^{(p)}}.\] (70) Это особенно справедливо для любого целого числа \(j\), для \(\chi=\rho^{j}\), где мы рассматриваем \(\rho:{\mathbb{Q}}^{\rm cyc,p}\to{\mathbb{C}}_{p}\) как гомоморфизм группы \(\rho:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{\mathcal{O}}^{\times}\). У нас есть \[\bigcap_{j\in{\mathbb{Z}}}\,{\rm Ker}\,h_{\rho^{j}}=\{0\}\] (71) will be translated as: \[\bigcap_{j\in{\mathbb{Z}}}\,{\rm Ker}\,h_{\rho^{j}}=\{0\}\] (71) поскольку инъективный характер конечной циклической группы порождает двойственную группу. Пусть \(n, m \in I(p)\) будут взаимно простыми. Тогда для любого \(j \in I(p)\) и \(z \in {\mathcal{O}}\) имеем: \[(\pi_{\sigma}(X)z\epsilon_{jm})_{jn}=\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{ -k}\frac{n}{m}))\,{\rm Fr}^{k}(z).\] (72) \[ (\pi_{\sigma}(X)z\epsilon_{jm})_{jn}=\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{ -k}\frac{n}{m}))\,{\rm Fr}^{k}(z).\] (72) Таким образом, если \(\pi_{\sigma}(X)=0\), то для всех \(j\) и \(m, n\), указанных выше, имеем \[\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))\,{\rm Fr}^{k}(z)=0 \qquad\text{для всех}\ z\in{\mathcal{O}}.\] (73) Для \(z\) - корня из единицы имеем \({\rm Fr}^{k}(z)=z^{p^{k}}\), следовательно, полином \[\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))\,Z^{p^{k+n}}\] would be translated to Russian as: \[\sum_{k\in{\mathbb{Z}}}h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))\,Z^{p^{k+n}}\] исчезает, при достаточно большом \(n\), на всех корнях из единицы, поэтому она тождественно равна нулю, отсюда все её коэффициенты должны обращаться в ноль, то есть \[h_{\rho^{j}}(y(p^{-k}\frac{n}{m}))=0\,,\quad\forall k\in{\mathbb{Z}},\ j\in {\mathbb{N}}.\] (74) Из (71) следует, что \(y(\frac{a}{b})=y(p^{-k}\frac{n}{m})=0\), отсюда (69) верно и доказательство того, что любой элемент из \({\rm Ker}\,\pi_{\sigma}\) находится в \({\mathcal{J}}_{p}\), завершено. Наконец, если \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) принадлежит \({\rm Ker}\,\pi_{\sigma}\), то в силу (69) имеем \(x\in{\mathcal{J}}_{p}^{0}\), и тем самым пересечение \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\cap{\mathcal{J}}_{p}\) является идеалом \({\mathcal{J}}_{p}^{0}\).∎ **Определение 6.7**. _Обозначим через \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) фактор алгебры \({\mathcal{H}}_{\mathbb{Z}}\) по идеалу \({\mathcal{J}}_{p}\), порожденному \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), \(\tilde{\mu}_{n}\), \(\mu_{n}^{*}\) для \(n\in I(p)\)._ Алгебра \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) порождена \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) операторами \(\tilde{\mu}_{n}\) и \(\mu_{n}^{*}\), где \(n\in I(p)\), и её представление аналогично представлению \({\mathcal{H}}_{\mathbb{Z}}\). Соотношения следующие: \[\begin{array}[]{l}\tilde{\mu}_{nm}=\tilde{\mu}_{n}\tilde{\mu}_{m}\,,\ \mu_{nm} ^{*}=\mu_{n}^{*}\mu_{m}^{*}\,,\quad~{}\forall n,m\in I(p)\\[8.535827pt] \mu_{n}^{*}\tilde{\mu}_{n}=n\,,\quad~{}\forall n\in I(p)\\[8.535827pt] \tilde{\mu}_{n}\mu_{m}^{*}=\mu_{m}^{*}\tilde{\mu}_{n}\,,\quad~{}\forall n,m\in I (p)\quad\text{с}~{}(n,m)=1\end{array}\] (75) Переведите математическую нотацию (маркдаун) с английского на русский язык. Сохраните формулы и соотношения. \[\begin{array}[]{l}\tilde{\mu}_{n}x\mu_{n}^{*}=\tilde{\rho}_{n}(x)\,,\ \mu_{n}^ {*}x=\sigma_{n}(x)\mu_{n}^{*}\,,\ x\tilde{\mu}_{n}=\tilde{\mu}_{n}\sigma_{n}(x )\end{array}\] (76) где \(\tilde{\rho}_{n}\), \(n\in I(p)\) определяется как \[\tilde{\rho}_{n}(e(\gamma))=\sum_{n\gamma^{\prime}=\gamma}e(\gamma^{\prime})\, ,\quad~{}\forall\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (77) (\77) Учитывая алгебру \({\mathcal{A}}\), автоморфизм \(\theta\in{\rm Aut}({\mathcal{A}})\) и целое число \(p\), мы позволяем \({\mathcal{A}}\rtimes_{\theta,\,p}{\mathbb{Z}}\) быть подалгеброй алгебраического кросс-произведения \(\{{\sum_{n\in{\mathbb{Z}}}}a_{n}V^{n}\mid a_{n}\in{\mathcal{A}}\}\), определенной условием. \[a_{-n}\in p^{n}{\mathcal{A}}\,,\quad~{}\forall n\in{\mathbb{N}}.\] (78) \[a_{-n} \in p^{n}{\mathcal{A}}, \quad ~{} \forall n \in{\mathbb{N}}.\] (78) Если мы позволим \(V=U^{*}\) и \(pV^{-1}=\tilde{U}\), то легко видеть, что \({\mathcal{A}}\rtimes_{\theta,\,p}{\mathbb{Z}}\) порождается \({\mathcal{A}},\tilde{U},U^{*}\) с соотношениями \[U^{*}\tilde{U}=p,\ \tilde{U}xU^{*}=p\theta^{-1}(x)\,,\ U^{*}x=\theta(x)U^{*}\, ,\ x\tilde{U}=\tilde{U}\theta(x)\,,\quad~{}\forall x\in{\mathcal{A}}.\] (79) \[U^{*}\tilde{U}=p,\ \tilde{U}xU^{*}=p\theta^{-1}(x)\,,\ U^{*}x=\theta(x)U^{*}\, ,\ x\tilde{U}=\tilde{U}\theta(x)\,,\quad~{}\forall x\in{\mathcal{A}}.\] (79) **Утверждение 6.8**: _Существует единственный автоморфизм \({\rm Fr}\in{\rm Aut}({\mathcal{H}}_{\mathbb{Z}}^{(p)})\), такой что_ \[{\rm Fr}(e(\gamma))=e(\gamma)^{p}\,,\quad~{}\forall\gamma\in{({\mathbb{Q}}/{ \mathbb{Z}})^{(p)}}\,,\ {\rm Fr}(\tilde{\mu}_{n})=\tilde{\mu}_{n}\,,\ {\rm Fr} (\mu_{n}^{*})=\mu_{n}^{*}\,,\quad~{}\forall n\in I(p).\] (80) _Один выводит изоморфизм_ \[{\mathcal{H}}_{\mathbb{Z}}/{\mathcal{J}}_{p}={\mathcal{H}}_{\mathbb{Z}}^{(p)} \rtimes_{{\rm Fr},\,p}{\mathbb{Z}}.\] (81) \[{\mathcal{H}}_{\mathbb{Z}}/{\mathcal{J}}_{p}={\mathcal{H}}_{\mathbb{Z}}^{(p)} \rtimes_{{\rm Fr},\,p}{\mathbb{Z}}.\] (81) Доказательство. Отображение \(\gamma\to p\gamma\) определяет автоморфизм \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Его линеаризация \({\rm Fr}\) действует на \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) и коммутирует с эндоморфизмами \(\sigma_{n}\) и \(\tilde{\rho}_{n}\). Фактически, применяя изоморфизм из Предложения 4.4, \({\rm Fr}\) соответствует автоморфизму Фробениуса \(\bar{\mathbb{F}}_{p}\). Таким образом, он расширяется до автоморфизма \({\rm Fr}\in{\rm Aut}({\mathcal{H}}_{\mathbb{Z}}^{(p)})\). Второе утверждение следует из сравнения представления \({\mathcal{H}}_{\mathbb{Z}}/{\mathcal{J}}_{p}\) с представлением крестового произведения \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\rtimes_{{\rm Fr},\,p}{\mathbb{Z}}\) как в (79). ∎ **Предложение 6.9**: _Пусть \(\sigma\in X_{p}\)._ Ограничение \(\pi_{\sigma}|_{{\mathcal{H}}_{\mathbb{Z}}^{(p)}}\) представления \(\pi_{\sigma}\) (как в Теореме 6.4) на \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) является \({\mathcal{O}}\)-линейным и неразложимым над \({\mathcal{O}}\). \((2)\) _Представления \(\pi_{\sigma}|_{{\mathcal{H}}_{\mathbb{Z}}^{(p)}}\) являются попарно неэквивалентными._ \((3)\) _Представление \(\pi_{\sigma}\) линейно и неразложимо над \({\mathbb{Z}}_{p}\)._ \((4)\) _Две представления \(\pi_{\sigma}\) и \(\pi_{\sigma^{\prime}}\) эквивалентны над \({\mathbb{Z}}_{p}\) тогда и только тогда, когда существует \(\alpha\in{\rm Aut}(\bar{\mathbb{F}}_{p})\) такое, что \(\sigma^{\prime}=\sigma\circ\alpha\)._ Доказательство: \((1)\) Cвойство \({\mathcal{O}}\)-линейности проверяется непосредственно на генераторах с использованием Теоремы 6.4. Из (62) следует, что вектор \(\epsilon_{1}\) является циклическим для \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\), то есть \(\pi_{\sigma}({\mathcal{H}}_{\mathbb{Z}}^{(p)})\,\epsilon_{1}\) плотно в \({\mathbb{W}}(\bar{\mathbb{F}}_{p})={\mathcal{O}}^{I(p)}\). Имеем \[\mathcal{O}\epsilon_{1}=\{\xi\in\mathbb{W}(\bar{\mathbb{F}}_{p})\mid\pi_{\sigma}(\mu_{n}^{*})(\xi)=0,\quad\forall n\neq 1,\ n\in I(p)\}.\] (82) Для любого непрерывного \({\mathcal{O}}\)-линейного оператора \(T\) в коммутанте \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) имеем \(\pi_{\sigma}(\mu_{n}^{*})T\epsilon_{1}=T\pi_{\sigma}(\mu_{n}^{*})\epsilon_{1}=0\), \(\forall n>1\) и по формуле (82) существует \(\lambda\in{\mathcal{O}}\) такое, что \(T\epsilon_{1}=\lambda\epsilon_{1}\). Так как \(\epsilon_{1}\) является циклическим вектором, \(T\) задается действием модуля \(\lambda\in{\mathcal{O}}\). \((2)\) По (62) действие \(\pi_{\sigma}(e(\gamma))\) для \(\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) на подпространство (82) определяется умножением на \(\rho(\gamma)\in{\mathcal{O}}\). Таким образом, \(\rho\) является инвариантом представления. \((3)\) Любой элемент коммутанта действия \({\mathcal{H}}_{\mathbb{Z}}\) представлен модульным действием \(\lambda\in{\mathcal{O}}\), где \(\lambda\) фиксировано для действия Фробениуса на \({\mathcal{O}}\), _т.е._\(\lambda\in{\mathbb{Z}}_{p}\). Это показывает, что \(\pi_{\sigma}\) неразложимый. \((4)\) Сначала покажем, что если существует \(\alpha\in{\rm Aut}(\bar{\mathbb{F}}_{p})\), такое что \(\sigma^{\prime}=\sigma\circ\alpha^{-1}\), то представления \(\pi_{\sigma}\) и \(\pi_{\sigma^{\prime}}\) эквивалентны над \({\mathbb{Z}}_{p}\). Пусть \(\tilde{\alpha}={\mathbb{W}}_{p^{\infty}}(\alpha)\in{\rm Aut}({\mathbb{W}}_{p^{ \infty}}(\bar{\mathbb{F}}_{p}))={\rm Aut}({\mathcal{O}})\) и определим \(U:{\mathcal{O}}^{I(p)}\to{\mathcal{O}}^{I(p)}\,,\ \ (U\xi)_{n}=\tilde{\alpha}( \xi_{n})\,,\quad~{}\forall n\in I(p)\). Имеем \(U\epsilon_{n}=\epsilon_{n}\) для всех \(n\in I(p)\) и если \(T\) является \({\mathcal{O}}\)-линейным оператором, то таковым является и \(UTU^{-1}\). Отсюда следует из (62) и (63), что \(U\pi_{\sigma}(\mu_{n})U^{-1}=\pi_{\sigma}(\mu_{n})\) и \(U\pi_{\sigma}(\mu_{n}^{*})U^{-1}=\pi_{\sigma}(\mu_{n}^{*})\). Для \(x\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), \(U\pi_{\sigma}(x)U^{-1}\) зависит только от \(r(x)\) и для \(x=e(a/b)\), \(b\in I(p)\), имеем \(U\pi_{\sigma}(e(a/b))U^{-1}\epsilon_{m}=\tilde{\alpha}(\rho(\zeta_{a/b}^{m})) \epsilon_{m}=\rho^{\prime}(\zeta_{a/b}^{m})\epsilon_{m}=\pi_{\sigma^{\prime}}( e(a/b))\). Кроме того, так как \(\tilde{\alpha}\) коммутирует с \({\rm Fr}\), из (64) следует, что \(U\pi_{\sigma}(\mu_{p})U^{-1}=\pi_{\sigma}(\mu_{p})\) и \(U\pi_{\sigma}(\mu_{p}^{*})U^{-1}=\pi_{\sigma}(\mu_{p}^{*})\). Таким образом, получаем требуемое равенство. Допустим, что два представления \(\pi_{\sigma}\) и \(\pi_{\sigma^{\prime}}\) эквивалентны над \({\mathbb{Z}}_{p}\). По (82) \({\mathbb{Z}}_{p}\)-линейное представление \(\pi_{\sigma}\) (и аналогично \(\pi_{\sigma^{\prime}}\)) единственным образом определяет следующее представление \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) в \({\mathbb{Z}}_{p}\)-модуле \({\mathcal{O}}\). \[\beta_{\sigma}(e(a/b))\xi=\rho(\zeta_{a/b})\xi\,,\quad~{}\forall\xi\in{ \mathcal{O}}.\] (83) \[\beta_{\sigma}(e(a/b))\xi=\rho(\zeta_{a/b})\xi\,,\quad~{}\forall\xi\in{ \mathcal{O}}.\] (83) В свою очередь это определяет расширение p-адической оценки на подполе \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\), порожденное над \({\mathbb{Q}}\) элементами \(\mu^{(p)}\). Действительно, формула \[{\rm val}(x)=\inf\{k\geq 0\mid\beta_{\sigma}(x){\mathcal{O}}\subset p^{k}{ \mathcal{O}}\}\,,\quad~{}\forall x\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}}) ^{(p)}}]\] (84) \[\text{(84)}: \, \text{{\rm val}}(x) = \inf\{k\geq 0 \mid \beta_{\sigma}(x){\mathcal{O}}\subset p^{k}{\mathcal{O}}\}\,,\quad~{}\forall x\in{\mathbb{Z}}[ {(\mathbb{Q}/{\mathbb{Z}}) ^{(p)} }]\] зависит только от класса \(x\) в \({\mathbb{Q}}^{\rm cyc,p}\) и единственным образом продолжается до оценки на \({\mathbb{Q}}^{\rm cyc,p}\). Заключение тогда следует из Предложения 8.14. ∎ ## 7. Теория KMS-системы BC при простом числе \(p\) В [4] было показано, что экстремальные комплексные состояния KMS ниже критической температуры для BC-системы (_см._ (24)) имеют форму \[\varphi_{\beta,\rho}(X)=\frac{{\rm Tr}(\pi_{\rho}(X)e^{-\beta H})}{{\rm Tr}(e^ {-\beta H})}\,,\quad~{}\forall X\in{\mathcal{H}}_{\mathbb{Z}}\] (85) где \(H\) - оператор Гамильтона умножения на \(\log n\) в каноническом базисе \(\epsilon_{n}\) гильбертового пространства \(\ell^{2}({\mathbb{N}})\), а \(\pi_{\rho}\) - несократимое представление алгебры \({\mathcal{H}}_{\mathbb{Q}}\), заданное \[\pi_{\rho}(\mu_{n})\epsilon_{m}=\epsilon_{nm},\ \ \pi_{\rho}(\mu_{n}^{*})=\pi_ {\rho}(\mu_{n})^{*}\,,\ \ \pi_{\rho}(e(a/b))\epsilon_{m}=\rho(\zeta_{a/b}^{m}) \epsilon_{m},\] (86) \[\pi_{\rho}(\mu_{n})\epsilon_{m}=\epsilon_{nm},\ \ \pi_{\rho}(\mu_{n}^{*})=\pi_ {\rho}(\mu_{n})^{*}\,,\ \ \pi_{\rho}(e(a/b))\epsilon_{m}=\rho(\zeta_{a/b}^{m}) \epsilon_{m},\] (86) где \(\rho\in\hat{\mathbb{Z}}^{*}\) определяет вложение в \({\mathbb{C}}\) циклотомического поля \({{\mathbb{Q}}^{\rm cyc}}\), порожденного абстрактными корнями из единицы. Таким образом, экстремальные состояния KMS \(\varphi_{\beta,\rho}\) могут быть вычислены непосредственно с использованием представления \(\pi_{\rho}\) и явного описания гамильтониана. ## В разделе 6 мы описали \(p\)-адический аналог представления \(\pi_{\rho}\). В этом разделе нашей целью является получение \(p\)-адического аналога состояний КМС \(\varphi_{\beta,\rho}\). Наравне с этим, уравнение, определяющее общую алгебраическую формулировку условия КМС, описывающее равенство \[\varphi(x\sigma(y))=\varphi(y\,x)\,,\quad~{}\forall x,y\in{\mathcal{A}},\] (87) \[\varphi(x\sigma(y))=\varphi(y\,x)\,,\quad~{}\forall x,y\in{\mathcal{A}},\] (87) где \(\varphi\) - линейная форма на алгебре \({\mathcal{A}}\), оснащенной автоморфизмом \(\sigma\in{\rm Aut}({\mathcal{A}})\). В нашем случае алгебра \[{\mathcal{A}}={\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}={\mathcal{H}}_{\mathbb{Z} }^{(p)}\otimes_{\mathbb{Z}}{\mathbb{C}}_{p}.\] (88) В §7.1 мы вводим, используя логарифм Ивасавы в качестве замены для комплексного гамильтониана \(H\), автоморфизмы \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\). Эти автоморфизмы определены для \(\beta\) в "расширенном \(s\)-диске" \(D_{p}\) (_см._ (91) ниже). В §7.5 мы покажем, как расширить их определение из области \(D_{p}\) до покрытия \(M\) \({\mathbb{C}}_{p}\). Конструкция KMS-состояний основана на классическом построении \(p\)-адических L-функций и \(p\)-адического полилогарифма, и многие свойства, которые мы получаем, основаны на упрощениях, происходящих, когда \(\beta=1-k(p-1)\) (\(k\in{\mathbb{Z}}\)). В §7.2 мы доказываем тождества в циклотомическом поле, включающие полиномы Бернулли, которые лежат в основе проверки условия KMS. В §7.3 мы предоставляем конструкцию линейных форм \(\varphi_{\beta,\rho}\), используя некоторые результаты из [37] (_см._ Глава V). В §7.4 мы доказываем, что функционалы \(\varphi_{\beta,\rho}\) удовлетворяют условию KMS относительно автоморфизма \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\). В отличие от комплексного случая, эта конструкция показывает (новое) явление инвариантности линейных форм \(\varphi_{\beta,\rho}\) относительно симметрии \({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\), заданной автоморфизмом \(e(\gamma)\mapsto e(-\gamma)\). В течение этого раздела мы фиксируем конечное, рациональное простое число \(p\) и алгебраическое замыкание \(\bar{\mathbb{Q}}_{p}\), его завершение обозначено \({\mathbb{C}}_{p}\). Мы также используем следующую нотацию \[q=4,\ \text{если}\ p=2,\qquad q=p,\ \text{если}\ p\neq 2\,.\] (89) and \[\varphi(q)=2,\ \text{if}\ p=2,\qquad\varphi(q)=p-1,\ \text{if}\ p\neq 2\,.\] (90) \[\varphi(q)=2,\ \text{если}\ p=2,\qquad\varphi(q)=p-1,\ \text{если}\ p\neq 2\,.\] (90) Мы рассматриваем "расширенный \(s\)-диск". \[D_{p}:=\{\beta\in{\mathbb{C}}_{p}\mid|\beta|_{p}<qp^{-1/(p-1)}>1\}\,,\ \\] (91) \[D_{p} := \{\beta \in {\mathbb{C}}_{p} \mid |\beta|_{p} < qp^{-1/(p-1)} > 1\}\,,\ \\] (91) и вначале разработаем теорию для \(\beta\in D_{p}\). В §7.5 мы объясним, как построение Ивасавы \(p\)-адических \(L\)-функций позволяет расширить всю теорию из области \(D_{p}\) на покрытие \({\mathbb{C}}_{p}\), заданное мультипликативной группой \(M\), которая является открытым диском радиусом один и центром в \(1\) в \({\mathbb{C}}_{p}\). ### Автоморфизмы \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) Пусть \({\mathbb{Z}}_{(p)}^{\times}\subset{\mathbb{Q}}^{\times}\) - это мультипликативная группа рациональных дробей, в которых числитель и знаменатель взаимно просты с \(p\). **Лемма 7.1**. _Пусть \(r\in{\mathbb{Z}}_{(p)}^{\times}\). Существует единственная аналитическая функция_ \[ D_{p}\to{\mathbb{C}}_{p},\quad\beta\mapsto r^{(\beta)} \] (92) \[ D_{p}\to{\mathbb{C}}_{p},\quad\beta\mapsto r^{(\beta)} \] (92) _так что_ \[r^{(\beta)}=r^{\beta}\,,\quad~{}\forall\beta=1-k\varphi(q).\] (93) \[r^{(\beta)}=r^{\beta}\,,\quad~{}\forall\beta=1-k\varphi(q).\] (93) Доказательство. Мы напомним, что логарифм Ивасавы \(\log_{p}\) является уникальным расширением функции, определенной в открытом единичном диске с центром в \(1\) по формуле \[-\log_{p}(1-x)=\sum_{n=1}^{\infty}\frac{x^{n}}{n}\,,\quad~{}\forall x\in{ \mathbb{C}}_{p},\ |x|_{p}<1\] (94) \[-\log_{p}(1-x)=\sum_{n=1}^{\infty}\frac{x^{n}}{n}\,,\quad~{}\forall x\in{ \mathbb{C}}_{p},\ |x|_{p}<1\] (94) в отображение \(\log_{p}:{\mathbb{C}}_{p}^{\times}\to{\mathbb{C}}_{p}\) такое, что \[\log_{p}(xy)=\log_{p}(x)+\log_{p}(y)\,,\quad~{}\forall x,y\in{\mathbb{C}}_{p} \,,\ \ \log_{p}(p)=0\,.\] (95) \[\log_{p}(xy)=\log_{p}(x)+\log_{p}(y)\,,\quad~{}\forall x,y\in{\mathbb{C}}_{p} \,,\ \ \log_{p}(p)=0\,.\] (95) У нас есть \(\log_{p}(-1)=0\) так как \(-1\) является корнем из единицы, и \[|\log_{p}(r)|_{p}\leq q^{-1}\,,\quad~{}\forall r\in{\mathbb{Z}}_{(p)}^{\times}.\] (96) \[|\log_{p}(r)|_{p}\leq q^{-1}\,,\quad~{}\forall r\in{\mathbb{Z}}_{(p)}^{\times}.\] (96) Более того, экспоненциальная функция определяется рядом \[{\rm exp}(x)=\sum_{n=1}^{\infty}\frac{x^{n}}{n!}\,,\quad~{}\forall x\in{ \mathbb{C}}_{p}\,,\ |x|_{p}<r_{p}=p^{-\frac{1}{p-1}}.\] (97) \[\exp(x)=\sum_{n=1}^{\infty}\frac{x^{n}}{n!}\,,\quad~{}\forall x\in{ \mathbb{C}}_{p}\,,\ |x|_{p}<r_{p}=p^{-\frac{1}{p-1}}.\] (97) Мы определяем \[r^{(\beta)}:=r\,{\rm exp}((\beta-1)\log_{p}(r))\,,\quad~{}\forall\beta\in D_{p}.\] (98) \[\Large r^{(\beta)}:=r\,{\rm exp}((\beta-1)\log_{p}(r))\,,\quad~{}\forall\beta\in D_{p}.\] (98) Это хорошо определенная аналитическая функция \(\beta\in D_{p}\), так как \(\beta-1\in D_{p}\) и, следовательно, \(|(\beta-1)\log_{p}(r)|_{p}<r_{p}\) по (96). Мы показываем, что (93) верно. Это следует из равенства. \[{\rm exp}(k\varphi(q)\log_{p}(r))=r^{k\varphi(q)}\,,\quad~{}\forall r\in{ \mathbb{Z}}_{(p)}^{\times},\ k\in{\mathbb{Z}}\] \[{\rm exp}(k\varphi(q)\log_{p}(r))=r^{k\varphi(q)}\,,\quad~{}\text{для всех}\ r\in{ \mathbb{Z}}_{(p)}^{\times},\ k\in{\mathbb{Z}}\] которая выполняется для \(r=-1\) так как \(\varphi(q)\) является четной. В общем случае, (93) следует из формулы \[{\rm exp}(n\log_{p}(a))=a^{n}\,,\quad~{}\forall a\in{\mathbb{Z}}_{p}^{*}\,,\ n \in\varphi(q){\mathbb{Z}}\] (99) \[\exp(n\log_{p}(a))=a^{n}\,,\quad~{}\forall a\in{\mathbb{Z}}_{p}^{*}\,,\ n \in\varphi(q){\mathbb{Z}}\] (99) как показано в [37] (Глава 5, стр. 52), где обозначение \[\langle a\rangle={\rm exp}(\log_{p}(a))\] (100) \[\langle a\rangle={\rm exp}(\log_{p}(a))\] (100) вводится. Уникальность следует из дискретности множества нулей аналитических функций. ∎ **Лемма 7.2****.**: _Пусть \(\beta\in D_{p}\), тогда_ \[{\mathbb{Z}}_{(p)}^{\times}\ni r\mapsto r^{(\beta)}\in{\mathbb{C}}_{p}^{\times}\] (101) \[{ \mathbb{Z}}_{(p)}^{\times}\in r\mapsto r^{(\beta)}\in{\mathbb{C}}_{p}^{\times}\] (101) _является гомоморфизмом группы. Более того, для \(r\in{\mathbb{Z}}_{(p)}^{\times}\)_ \[r^{(\beta_{1})}r^{(\beta_{2})}=r^{(\beta_{1}+\beta_{2})}r^{(0)}\,,\quad~{} \forall\beta_{j}\in D_{p}\] (102) \[r^{(\beta_{1})}r^{(\beta_{2})}=r^{(\beta_{1}+\beta_{2})}r^{(0)}\,,\quad~{} \forall\beta_{j}\in D_{p}\] (102) Доказательство: Это следует из (95) и равенства (сравнительн. [32]) \[{\rm exp}(x_{1}+x_{2})={\rm exp}(x_{1}){\rm exp}(x_{2})\,,\quad~{}\forall x_{j },\ |x_{j}|_{p}<r_{p}.\] (103) \[{\rm exp}(x_{1}+x_{2})={\rm exp}(x_{1}){\rm exp}(x_{2})\,,\quad~{}\forall x_{j },\ |x_{j}|_{p}<r_{p}.\] (103) ∎ Необходимо-: Стандартное обозначение для \(r^{(0)}\) - \(\omega(r)\): это единственный \(\varphi(q)\) корень из единицы, который сравним с \(r\) по модулю \(q\). В частности, имеем \[(r^{(0)})^{\varphi(q)}=1\,,\quad~{}\forall r\in{\mathbb{Z}}_{(p)}^{\times}.\] (104) \[(r^{(0)})^{\varphi(q)}=1\,,\quad~{}\forall r\in{\mathbb{Z}}_{(p)}^{\times}.\] (104) **Утверждение 7.3.**: \((1)\) _Для \(\beta\in D_{p}\) существует единственный автоморфизм \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\), такой что_ \[\sigma^{(\beta)}(\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*})=\left(\frac{b}{a}\right) ^{(\beta)}\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*}\,,\quad~{}\forall a,b\in I(p),\ \gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}. \] (105) \((2)\) _У нас есть_ \[\sigma^{(\beta_{1})}\circ\sigma^{(\beta_{2})}=\sigma^{(\beta_{1}+\beta_{2})} \circ\sigma^{(0)}\,,\quad~{}\forall\beta_{j}\in D_{p}\] (106) \[\sigma^{(\beta_{1})}\circ\sigma^{(\beta_{2})}=\sigma^{(\beta_{1}+\beta_{2})} \circ\sigma^{(0)}\,,\quad~{}\forall\beta_{j}\in D_{p}\] (106) _и \(\sigma^{(0)}\) — автоморфизм порядка \(\varphi(q)\)._ Доказательство. Достаточно проверить, что \(\sigma^{(\beta)}\) сохраняет представление, заданное отношениями (75) и (76). Это следует из мультипликативности, показанной в Лемме 7.2. Аналогично, (106) следует из (102). Последнее утверждение следует из (104).∎ ### Циклотомические тождества для полилогарифма Cyclotomic identities for the polylogarithm can be represented by the following equations: 1. **Identity 1:**  where  is the polylogarithm function of order *s*, 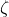 is the Riemann zeta function, and  is the imaginary unit. 2. **Identity 2:**  where  and 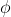 are the imaginary and real parts of , respectively. These identities play a crucial role in various areas of mathematics and have significant applications in number theory, complex analysis, and algebraic geometry. Мы напоминаем, что многочлены Бернулли \(B_{n}(u)\) определяются индуктивно следующим образом: \[B_{0}(x)=1\,,\ \ B^{\prime}_{n}(x)=nB_{n-1}(x)\,,\ \ \int_{0}^{1}B_{n}(x)dx=0.\] \[B_{0}(x)=1\,,\ \ B^{\prime}_{n}(x)=nB_{n-1}(x)\,,\ \ \int_{0}^{1}B_{n}(x)dx=0.\] Эти полиномы могут быть введены эквивалентно, используя функцию-генератор. \[\[F(u,t)=\frac{te^{ut}}{e^{t}-1}=\sum_{n=0}^{\infty}B_{n}(u)\frac{t^{n}}{n!}.\]\] (107) Первые几 - \[B_{0}(u) = 1\] \[B_{1}(u) = -\frac{1}{2}+u\] \[B_{2}(u) = \frac{1}{6}-u+u^{2}\] \[B_{3}(u) = \frac{u}{2}-\frac{3u^{2}}{2}+u^{3}\] \[B_{4}(u) = -\frac{1}{30}+u^{2}-2u^{3}+u^{4}\] \[B_{5}(u) = -\frac{u}{6}+\frac{5u^{3}}{3}-\frac{5u^{4}}{2}+u^{5}.\] Эти полиномы удовлетворяют уравнению \(B_{n}(1-u)=(-1)^{n}B_{n}(u)\). Числа Бернулли обозначаются как \(B_{n}=B_{n}(0)\). Используя (107), можно проверить тождество (_cf._[37], Глава 4, Предложение 4.1) \[g^{n-1}\sum_{j=0}^{g-1}B_{n}(\frac{x+j}{g})=B_{n}(x)\,.\] (108) \[g^{n-1}\sum_{j=0}^{g-1}B_{n}(\frac{x+j}{g})=B_{n}(x)\,.\] (108) Мы также вводим индуктивно рациональные дроби \(\ell_{\beta}(z)\) для \(\beta\in-{\mathbb{N}}\) следующим образом \[\partial_{z}\ell_{\beta}(z)=\frac{\ell_{\beta-1}(z)}{z}\,,\ \ell_{0}(z)=\frac{z}{1-z}.\] (109) Для \(\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\) мы обозначаем через \(\zeta_{\alpha}\in{{\mathbb{Q}}^{\rm cyc}}\) класс \(e(\alpha)\in{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) по модулю циклотомического идеала (_см._ Определение 8.1). Он является примитивным корнем из единицы, порядок которого равен знаменателю \(\alpha\). **Лемма 7.4****.**: _Пусть \(n>1\), \(a, b\in{\mathbb{N}}\). Тогда_ \[b^{n-1}\sum_{j=0}^{b-1}\zeta_{a/b}^{j}B_{n}(\frac{j}{b})=\left\{\begin{array}[ ]{ll}-n\ell_{1-n}(\zeta_{a/b}),&\hbox{если}\ \zeta_{a/b}\neq 1\\ B_{n},&\hbox{если}\ \zeta_{a/b}=1.\end{array}\right.\] (110) Доказательство.: Равенство (110) для \(\zeta_{a/b}=1\) следует из (108). Таким образом, мы можем предположить, что \(z=\zeta_{a/b}\neq 1\). Разложение Тейлора в точке \(t=0\) для \((ze^{t}-1)^{-1}\) задано \[(ze^{t}-1)^{-1}=(z-1)^{-1}-\sum_{n=1}^{\infty}\ell_{-n}(z)\frac{t^{n}}{n!}\] (111) поскольку \((z-1)^{-1}=-1-\ell_{0}(z)\) и \(\partial_{t}\) согласуется с \(z\partial_{z}\). Тогда для \(b\in{\mathbb{N}}\) и \(t\), таких что \(ze^{\frac{t}{b}}\neq 1\), одно имеет \[\sum_{j=0}^{b-1}z^{j}e^{\frac{j}{b}t}=\frac{z^{b}e^{t}-1}{ze^{\frac{t}{b}}-1}.\] would be translated to Russian as: \[\sum_{j=0}^{b-1}z^{j}e^{\frac{j}{b}t}=\frac{z^{b}e^{t}-1}{ze^{\frac{t}{b}}-1}.\] Так как \(z^{b}=1\), можно получить \[\sum_{n=0}^{\infty}\left(\sum_{j=0}^{b-1}z^{j}B_{n}(\frac{j}{b})\right)\frac{t ^{n}}{n!}=\sum_{j=0}^{b-1}z^{j}F(\frac{j}{b},t)=\frac{t}{ze^{\frac{t}{b}}-1}.\] \[\sum_{n=0}^{\infty}\left(\sum_{j=0}^{b-1}z^{j}B_{n}(\frac{j}{b})\right)\frac{t ^{n}}{n!}=\sum_{j=0}^{b-1}z^{j}F(\frac{j}{b},t)=\frac{t}{ze^{\frac{t}{b}}-1}.\] Поскольку \(z\neq 1\), разложение Тейлора в \(t=0\) с использованием (111) дает равенство \[\sum_{j=0}^{b-1}z^{j}B_{n}(\frac{j}{b})=-\frac{n}{b^{n-1}}\ell_{1-n}(z),\qquad \forall n>1\,.\] (112) \[\sum_{j=0}^{b-1}z^{j}B_{n}(\frac{j}{b})=-\frac{n}{b^{n-1}}\ell_{1-n}(z),\qquad \text{для всех } n>1\,.\] (112) ∎ **Утверждение 7.5**. _Пусть \(n>1\), \(a,b\in{\mathbb{N}}\)._ \((1)\) _Следующая сумма зависит только от \(n\) и того, что \(\frac{a}{b}\in{\mathbb{Q}}/{\mathbb{Z}}\)_ \[Y_{n}(a/b)=f^{n-1}\sum_{j=0}^{f-1}\zeta_{a/b}^{j}B_{n}(\frac{j}{f})\,,\quad~{} \forall f\in b{\mathbb{N}},\ f\neq 0.\] (113) \[Y_{n}(a/b)=f^{n-1}\sum_{j=0}^{f-1}\zeta_{a/b}^{j}B_{n}(\frac{j}{f})\,,\quad~{} \forall f\in b{\mathbb{N}},\ f\neq 0.\] (113) \((2)\) _У нас есть_ \[ \frac{1}{b}\sum_{a=0}^{b-1}Y_{n}(a/b)=b^{n-1}B_{n}=b^{n-1}Y_{n}(0).\] (114) \[ \frac{1}{b}\sum_{a=0}^{b-1}Y_{n}(a/b)=b^{n-1}B_{n}=b^{n-1}Y_{n}(0).\] (114) \((3)\) _Для \(g\geq 1\), \(x^{g}\neq 1\) мы имеем_ \[\frac{1}{g}\sum_{j=0}^{g-1}\ell_{1-n}(\zeta_{j/g}\,x)=g^{n-1}\ell_{1-n}(x^{g}).\] (115) \[\frac{1}{g}\sum_{j=0}^{g-1}\ell_{1-n}(\zeta_{j/g}\,x)=g^{n-1}\ell_{1-n}(x^{g}).\] (115) Доказательство: \((1)\) следует из (110). Чтобы получить \((2)\), заметим, что \[\frac{1}{b}\sum_{a=0}^{b-1}\zeta_{a/b}^{j}=0\,,\quad~{}\forall j\neq 0\ (b)\,, \ \ \frac{1}{b}\sum_{a=0}^{b-1}\zeta_{a/b}^{j}=1\,,\quad~{}\forall j=0\ (b).\] \[\frac{1}{b}\sum_{a=0}^{b-1}\zeta_{a/b}^{j}=0\,,\quad~{}\forall j\neq 0\ (b)\,, \ \ \frac{1}{b}\sum_{a=0}^{b-1}\zeta_{a/b}^{j}=1\,,\quad~{}\forall j=0\ (b).\] \((3)\) Определение (115) проверяется как тождество между рациональными дробями с помощью индукции по \(n\in{\mathbb{N}}\). Для \(n=1\) оно следует из применения операции \(-z\partial_{z}\log()\) к обеим сторонам тождества. \[\prod_{j=0}^{g-1}(1-\zeta_{j/g}z)=1-z^{g}.\] Чтобы получить (115) для \(n\), предполагая его для \(n-1\), применяется операция \(z\partial_{z}\) к обеим сторонам тождества для \(n-1\). ∎ Объединяя (115) с (110), получаем, используя (114), когда \(\alpha\in{\mathbb{Z}}\) \[\frac{1}{b}\sum_{j=0}^{b-1}Y_{n}(\frac{\alpha+j}{b})=b^{n-1}Y_{n}(\alpha)\,, \quad~{}\forall\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\] (116) \[\frac{1}{b}\sum_{j=0}^{b-1}Y_{n}(\frac{\alpha+j}{b})=b^{n-1}Y_{n}(\alpha)\,, \quad~{}\text{для всех }\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\] (116) ### Линейные формы \(\varphi_{\beta,\rho}\) В этом разделе мы дадим значение выражениям вида \[Z_{\rho}\left(\frac{a}{b},\beta\right)=\sum_{m\in I(p)}\rho\left(\zeta_{a/b}^{m}\right)\,m^{-\beta}, \qquad\beta\in D_{p}\] (117) где \(\frac{a}{b}\in{\mathbb{Q}}\), \(b\in I(p)\) является целым числом, взаимно простым с \(p\), и \(\rho:{{\mathbb{Q}}^{\rm cyc}}\hookrightarrow{\mathbb{C}}_{p}\). Обратите внимание, что как функция от \(m\in I(p)\), \(\rho(\zeta_{a/b}^{m})\) зависит только от остатка \(m\) по модулю \(b\). Пусть \(f=bp\) и раскладываем сумму (117) по остатку \(\alpha\) от \(m\) по модулю \(f\). Для этого имеем \({\mathbb{Z}}/f{\mathbb{Z}}={\mathbb{Z}}/p{\mathbb{Z}}\times{\mathbb{Z}}/b{ \mathbb{Z}}\). Элементы \(I(p)\) характеризуются тем, что их остатки по модулю \(f\) заданы парами \(\alpha=(\alpha_{1},\alpha_{2})\in{\mathbb{Z}}/f{\mathbb{Z}}\), где \(\alpha_{1}\neq 0\). Для \(\alpha\in({\mathbb{Z}}/p{\mathbb{Z}})^{\times}\times{\mathbb{Z}}/b{\mathbb{Z}}\) пусть \(\tilde{\alpha}\in{\mathbb{N}}\) будет наименьшим целым числом с остатком по модулю \(f\), равным \(\alpha\). Тогда сумму (117) можно записать как \[Z_{\rho}(\frac{a}{b},\beta)=\sum_{\alpha}\rho(\zeta_{a/b}^{\alpha})\,\sum_{n \geq 0}(\tilde{\alpha}+fn)^{-\beta},\qquad\beta\in D_{p}.\] (118) Обратите внимание, что первая сумма (по \(\alpha\)) в (118) содержит только конечное количество слагаемых. Каждая бесконечная сумма в (118) имеет вид (с \(z=\tilde{\alpha}/f\)) \[\sum_{n\in{\mathbb{N}}}(\tilde{\alpha}+fn)^{-\beta}=f^{-\beta}\,\sum_{n\in{ \mathbb{N}}}(z+n)^{-\beta},\qquad\beta\in D_{p}\] (119) и хорошо известно, что это выражение сохраняет смысл в \(p\)-адическом контексте (см. [37] Глава V). Более точно, асимптотическое разложение в комплексном случае для \(z\to\infty\) (этот процесс восходит к вычислению Эйлера \(\sum_{1}^{\infty}n^{-2}\)) \[\sum_{n=0}^{\infty}(z+n)^{-\beta}\sim\frac{z^{1-\beta}}{\beta-1}\sum_{0}^{ \infty}\binom{1-\beta}{j}B_{j}z^{-j}\] Перевод: \[\sum_{n=0}^{\infty}(z+n)^{-\beta}\sim\frac{z^{1-\beta}}{\beta-1}\sum_{0}^{ \infty}\binom{1-\beta}{j}B_{j}z^{-j}\] мотивирует следующую точную формулу, где мы предпочитаем оставить некоторую свободу в выборе множителя \(f\) для \(bq\). **Лемма 7.6**: _Пусть \(q\) как в (91), и \(f\in{\mathbb{N}}\), \(f\neq 0\), кратное \(bq\), выражение_ \[Z_{\rho}(\frac{a}{b},\beta,f):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{ \mathbb{N}}}\rho(\zeta_{a/b}^{c})\,\frac{\langle c\rangle^{1-\beta}}{\beta-1} \sum_{j=0}^{\infty}\binom{1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j},\qquad \beta\in D_{p},\] (120) _определяет мероморфную функцию \(\beta\in D_{p}\) с однополюсом в точке \(\beta=1\)._ Доказательство:. Следует из [37] (Утверждение 5.8) и неравенства (_см._[37] Теорема 5.10) \[|\left(\frac{f}{c}\right)^{j}B_{j}|_{p}\leq p|f|_{p}^{j}\] \[|\left(\frac{f}{c}\right)^{j}B_{j}|_{p}\leq p|f|_{p}^{j}\] что ряд \[\sum_{j=0}^{\infty}\binom{{1-\beta}}{{j}}\left(\frac{{f}}{{c}}\right)^{{j}}B_{{j}}\] сходится для \(|\beta|_{p}<|f|_{p}^{-1}p^{-\frac{1}{p-1}}\geq qp^{-\frac{1}{p-1}}>1\).∎ **Лемма 7.7**: _Для \(\beta\) отрицательного нечетного целого вида \(\beta=1-m=1-k\varphi(q)\) и \(f\in{\mathbb{N}}\), \(f\neq 0\), \(f\) кратно \(bq\), имеет место следующее соотношение, где \(Y_{m}\) определено как (113)_ \[Z_{\rho}\left(\frac{a}{b},\beta,f\right)=-\frac{1}{m}\rho\left(Y_{m}\left(\frac{a}{b} \right)-p^{m-1}Y_{m}\left(\frac{pa}{b}\right)\right)\,. (121)\] Доказательство: Для \(1\leq c<f\), \(c\notin p{\mathbb{N}}\), имеем \(\langle c\rangle^{1-\beta}=c^{m}\). Биномиальные коэффициенты \(\binom{1-\beta}{j}\) в (120) все исчезают для \(j>m\), и сумма, определяющая \(Z(\frac{a}{b},\beta,f)\), следовательно, является конечной. У нас есть \[\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1-\beta}{j }\left(\frac{f}{c}\right)^{j}B_{j}=-\frac{c^{m}}{m}\sum_{j=0}^{m}\binom{m}{j} \left(\frac{f}{c}\right)^{j}B_{j}.\] translates to: \[\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1-\beta}{j }\left(\frac{f}{c}\right)^{j}B_{j}=-\frac{c^{m}}{m}\sum_{j=0}^{m}\binom{m}{j} \left(\frac{f}{c}\right)^{j}B_{j}.\] Кроме того, для любого целого числа \(m>0\), многочлены Бернулли удовлетворяют уравнению \[\sum_{j=0}^{m}\binom{m}{j}z^{-j}B_{j}=z^{-m}B_{m}(z)\,.\] переводится на русский язык следующим образом: \[\sum_{j=0}^{m}\binom{m}{j}z^{-j}B_{j}=z^{-m}B_{m}(z)\,.\] Для \(1\leq c<f\), \(c\notin p{\mathbb{N}}\), получаем, взяв \(z=\frac{c}{f}\) \[\frac{1}{f}\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom {1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j}=-\frac{f^{m-1}}{m}B_{m}\left( \frac{c}{f}\right)\,.\] (122) \[\frac{1}{f}\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom {1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j}=-\frac{f^{m-1}}{m}B_{m}\left( \frac{c}{f}\right)\,.\] (122) Определим для любого \(c\in{\mathbb{N}}\) \[T(c):=-\frac{f^{m-1}}{m}B_{m}\left(\frac{c}{f}\right).\] (123) \[Т(с):=-\frac{f^{m-1}}{m}B_{m}\left(\frac{c}{f}\right).\] (123) Одно имеет \[Z_{\rho}(\frac{a}{b},\beta,f)=\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}T(c) \rho(\zeta_{a/b}^{c})=\sum_{0\leq c<f}T(c)\rho(\zeta_{a/b}^{c})-\sum_{c=jp \atop 0\leq j<f/p}T(c)\rho(\zeta_{a/b}^{c}).\] \[Z_{\rho}(\frac{a}{b},\beta,f)=\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}T(c) \rho(\zeta_{a/b}^{c})=\sum_{0\leq c<f}T(c)\rho(\zeta_{a/b}^{c})-\sum_{c=jp \atop 0\leq j<f/p}T(c)\rho(\zeta_{a/b}^{c}).\] С того факта, что \(b\) делит \(f\), следует \[\sum_{0\leq c<f}T(c)\rho(\zeta_{a/b}^{c})=-\frac{f^{m-1}}{m}\sum_{0\leq c<f} \rho(\zeta_{a/b}^{c})B_{m}\left(\frac{c}{f}\right)=-\frac{1}{m}\rho(Y_{m}( \zeta_{a/b}))\] в то время как, так как \(b\) делит \(f/p=f^{\prime}\), мы получаем \[\sum_{c=jp\atop 0\leq j<f/p}T(c)\rho(\zeta_{a/b}^{c})=-\frac{f^{m-1}}{m}\sum_{ 0\leq j<f/p}\rho(\zeta_{a/b}^{jp})B_{m}\left(\frac{j}{f^{\prime}}\right)=- \frac{p^{m-1}}{m}\rho(Y_{m}(\zeta_{a/b}^{p})).\] Равенство (121) следует. ∎ **Corollary 7.8****.**: _Функция_ \[Z_{\rho}(\frac{a}{b},\beta):=Z_{\rho}\left(\frac{a}{b},\beta,f\right)\] (124) _не зависит от выбора \(f\in bq{\mathbb{N}}\), \(f\neq 0\)._ Доказательство: Для двух выборов \(f, f^{\prime}\) аналитическая функция \(\beta\in D_{p}\) \[(\beta-1)(Z_{\rho}(\frac{a}{b},\beta,f)-Z_{\rho}(\frac{a}{b},\beta,f^{\prime}))\] \[(\beta-1)(Z_{\rho}(\frac{a}{b},\beta,f)-Z_{\rho}(\frac{a}{b},\beta,f^{\prime}))\] обращается в нуль при всех отрицательных целых \(1-k\varphi(q)\) по равенству (121), следовательно, он тождественно равен \(0\).∎ **Теорема 7.9**: _Следующее уравнение определяет линейную форму \(\varphi_{\beta,\rho}\) на \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) для любого \(\beta\in D_{p}\)_ \[\varphi_{\beta,\rho}(\tilde{\mu}_{n}e(\frac{a}{b})\mu_{m}^{*})=\left\{\begin{ array}[]{ll}Z_{\rho}(\frac{a}{b},\beta)&\hbox{если}\ n=m=1\,,\\ 0&\hbox{в противном случае,}\end{array}\right.\] (125) _для \(n, m \in I(p)\), взаимнопростые._ Следующая лемма будет играть важную роль в доказательстве (см. следующий раздел), что \(\varphi_{\beta,\rho}\) удовлетворяет условию KMS. **Лемма 7.10****.**: _Для любого \(n\in I(p)\) и \(\beta\in D_{p}\), \(\beta\neq 1\), выполнено_ \[\varphi_{\beta,\rho}(\tilde{\rho}_{n}(X))=\langle n\rangle^{1-\beta}\varphi_{ \beta,\rho}(X)\,,\quad~{}\forall X\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}}) ^{(p)}}]\] (126) \[\varphi_{\beta, \rho} (\tilde{\rho}_n(X)) = \langle n \rangle^{1-\beta} \varphi_{\beta, \rho}(X)\,,\quad~{}\forall X\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}}) ^{(p)}}]\] (126) _(см. (77) для определения \(\tilde{\rho}_{n}\))._ Доказательство. После умножения на \(\beta-1\) обе стороны (126) являются аналитическими функциями от \(\beta\in D_{p}\). Таким образом, достаточно показать, что (126) выполняется для \(\beta=1-k\varphi(q)=1-m\). В этом случае имеем \(\langle n\rangle^{1-\beta}=n^{m}\), и из (121) получаем \[\varphi_{\beta,\rho}(e(\gamma))=-\frac{1}{m}\rho\left(Y_{m}(\gamma)-p^{m-1}Y_{ m}(p\gamma)\right)\,,\quad~{}\forall\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p) }}.\] \[\varphi_{\beta,\rho}(e(\gamma))=-\frac{1}{m}\rho\left(Y_{m}(\gamma)-p^{m-1}Y_{ m}(p\gamma)\right)\,,\quad~{}\text{для всех }\gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p) }}.\] Чтобы доказать равенство (126), мы можем предположить, что \(X=e(\alpha)\) для \(\alpha\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Получается \[\tilde{\rho}_{n}(X)=\sum_{j=0}^{n-1}e(\frac{\alpha+j}{n})\] \[\tilde{\rho}_{n}(X)=\sum_{j=0}^{n-1}e(\frac{\alpha+j}{n})\] чтобы \[\varphi_{\beta,\rho}(\tilde{\rho}_{n}(X))=-\frac{1}{m}\sum_{j=0}^{n-1}\rho \left(Y_{m}(\frac{\alpha+j}{n})-p^{m-1}Y_{m}(p\frac{\alpha+j}{n})\right).\] \[\varphi_{\beta, \rho}(\tilde{\rho}_{n}(X)) = -\frac{1}{m}\sum_{j=0}^{n-1}\rho \left(Y_{m}\left(\frac{\alpha+j}{n}\right)-p^{m-1}Y_{m}\left(p\frac{\alpha+j}{n}\right)\right).\] Тогда (126) следует из (116). Поскольку \(p\) взаимно просто с \(n\) и рациональные числа \(p\frac{\alpha+j}{n}\in{\mathbb{Q}}/{\mathbb{Z}}\) образуют ту же подмножество, что и множество, состоящее из \(\frac{p\alpha+j}{n}\), мы получаем \[\sum_{j=0}^{n-1}Y_{m}\left(\frac{\alpha+j}{n}\right)=n^{m}Y_{m}(\alpha)\,,\ \ \sum_{j=0}^ {n-1}Y_{m}\left(p\frac{\alpha+j}{n}\right)=n^{m}Y_{m}(p\alpha).\] ∎ ### Условие KMS\({}_{\beta}\) Основным результатом этого раздела является следующее **Теорема 7.11**. Для любого \(\beta\in D_{p}\), \(\beta\neq 1\) и \(\rho:{\mathbb{Q}}^{\rm cyc,p}\hookrightarrow{\mathbb{C}}_{p}\), линейная форма \(\varphi_{\beta,\rho}\) удовлетворяет условию KMS\({}_{\beta}\): \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=\varphi_{\beta,\rho}(y\,x)\,,\quad~ {}\forall x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}.\] (127) \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=\varphi_{\beta,\rho}(y\,x)\,,\quad~ {}\forall x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}.\] (127) _Более того, функция разбиения - это \(p\)-адическая \(L\)-функция._ \[Z(\beta):\ \varphi_{\beta,\rho}(1)=L_{p}(\beta,1)\] (128) _который не обращается в нуль для \(\beta\in D_{p}\)._ Доказательство: Мы фиксируем \(x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\), затем после умножения на \(\beta-1\), обе стороны уравнения (127) становятся аналитическими функциями от \(\beta\in D_{p}\). Сначала мы предполагаем, что \(\beta\neq 1\); случай \(\beta=1\) мы рассмотрим отдельно позже. Поскольку любой элемент алгебры \({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\) может быть записан как конечная линейная комбинация \(\tilde{\mu}_{n}X\mu_{m}^{*}\), где \(X\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\), мы можем предположить, что \[x=\tilde{\mu}_{n}X\mu_{m}^{*}\,,\ \ y=\tilde{\mu}_{s}Y\mu_{t}^{*}\] => \[x=\tilde{\mu}_{n}X\mu_{m}^{*}\,,\ \ y=\tilde{\mu}_{s}Y\mu_{t}^{*}\] где \(n,m\in I(p)\), \((n,m)=1\), \(s,t\in I(p)\), \((s,t)=1\) и \(X,Y\in{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\). Затем, мы используем представление \({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}\) для вычисления \(xy=\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}\). Пусть \(u\) - НОД \(m=um^{\prime}\) и \(s=us^{\prime}\). Данное выражение вычисляется следующим образом: \[\mu^{*}_{m}\,\tilde{\mu}_{s}=\mu^{*}_{m^{\prime}}\,\mu^{*}_{u}\,\tilde{\mu}_{u }\tilde{\mu}_{s^{\prime}}=u\mu^{*}_{m^{\prime}}\,\tilde{\mu}_{s^{\prime}}=u\, \tilde{\mu}_{s^{\prime}}\mu^{*}_{m^{\prime}}\] \[\mu^{*}_{m}\,\tilde{\mu}_{s}=\mu^{*}_{m^{\prime}}\,\mu^{*}_{u}\,\tilde{\mu}_{u }\tilde{\mu}_{s^{\prime}}=u\mu^{*}_{m^{\prime}}\,\tilde{\mu}_{s^{\prime}}=u\, \tilde{\mu}_{s^{\prime}}\mu^{*}_{m^{\prime}}\] \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{n}\,X\,\tilde{\mu}_{s^{\prime}}\mu^{*}_{m^{\prime}}\,Y\,\mu^{*}_{t}=\,u\, \tilde{\mu}_{n}\,\tilde{\mu}_{s^{\prime}}\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(Y)\mu^{*}_{m^{\prime}}\,\mu^{*}_{t}\] Пусть \(v\) будет НОДом \(ns^{\prime}=vw\) и \(m^{\prime}t=vz\). Имеем \(\tilde{\mu}_{n}\,\tilde{\mu}_{s^{\prime}}=\tilde{\mu}_{w}\,\tilde{\mu}_{v}\), \(\mu^{*}_{m^{\prime}}\,\mu^{*}_{t}=\mu^{*}_{v}\,\mu^{*}_{z}\). \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{w}\,\tilde{\mu}_{v}\,\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(y)\,\mu^{*}_ {v}\,\mu^{*}_{z}=u\,\tilde{\mu}_{w}\,\tilde{\rho}_{v}(\sigma_{s^{\prime}}(X) \sigma_{m^{\prime}}(Y))\,\mu^{*}_{z}\,.\] \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{w}\,\tilde{\mu}_{v}\,\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(y)\,\mu^{*}_ {v}\,\mu^{*}_{z}=u\,\tilde{\mu}_{w}\,\tilde{\rho}_{v}(\sigma_{s^{\prime}}(X) \sigma_{m^{\prime}}(Y))\,\mu^{*}_{z}\,.\] Мы получаем \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{w}\,\tilde{\rho}_{v}(\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(Y))\,\mu^{*} _{z}\,,\ \ \frac{w}{z}=\frac{n}{m}\frac{s}{t}.\] (129) (129) \[\tilde{\mu}_{n}\,X\,\mu^{*}_{m}\,\tilde{\mu}_{s}\,Y\,\mu^{*}_{t}=u\,\tilde{\mu }_{w}\,\tilde{\rho}_{v}(\sigma_{s^{\prime}}(X)\sigma_{m^{\prime}}(Y))\,\mu^{*} _{z}\,,\ \ \frac{w}{z}=\frac{n}{m}\frac{s}{t}.\] Отсюда следует, что если не выполняется условие \(s=m\) и \(t=n\), то \(\frac{w}{z}\neq 1\) и. \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=\varphi_{\beta,\rho}(y\,x)=0.\] (130) \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=\varphi_{\beta,\rho}(y\,x)=0.\] (130) Таким образом, мы можем предположить, что \(s=m\) и \(t=n\). Затем у нас есть \[x\sigma^{(\beta)}(y)=m\left(\frac{n}{m}\right)^{(\beta)}\tilde{\mu}_{n}\,XY\, \mu^{*}_{n}=m\left(\frac{n}{m}\right)^{(\beta)}\tilde{\rho}_{n}(XY)\] \[x\sigma^{(\beta)}(y)=m\left(\frac{n}{m}\right)^{(\beta)}\tilde{\mu}_{n}\,XY\, \mu^{*}_{n}=m\left(\frac{n}{m}\right)^{(\beta)}\tilde{\rho}_{n}(XY)\] таким образом, с помощью (126) получаем \[\varphi_{\beta,\rho}(x\sigma^{(\beta)}(y))=m\left(\frac{n}{m}\right)^{(\beta)} \left\langle n\right\rangle^{1-\beta}\varphi_{\beta,\rho}(XY).\] (131) Аналогично имеем, применяя снова (126) \[yx=n\tilde{\mu}_{m}YX\mu_{m}^{*}\,,\ \ \varphi_{\beta,\rho}(y\,x)=n\langle m \rangle^{1-\beta}\varphi_{\beta,\rho}(XY).\] \[yx=n\tilde{\mu}_{m}YX\mu_{m}^{*}\,,\ \ \varphi_{\beta,\rho}(y\,x)=n\langle m \rangle^{1-\beta}\varphi_{\beta,\rho}(XY).\] Таким образом, (127) следует из равенства. \[m\left(\frac{n}{m}\right)^{(\beta)}\langle n\rangle^{1-\beta}=n\langle m \rangle^{1-\beta}\] will be translated to Russian as follows: \[m\left(\frac{n}{m}\right)^{(\beta)}\langle n\rangle^{1-\beta}=n\langle m \rangle^{1-\beta}\] который в свою очередь происходит из (98) и (100). Теперь мы обратимся к нормализационному коэффициенту (_т.е._ функции разбиения) в (125), которая задается уравнением \[Z(\beta):=\varphi_{\beta,\rho}(1)=\frac{1}{q}\sum_{1\leq c<q\atop c\notin p{ \mathbb{N}}}\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty} \binom{1-\beta}{j}\left(\frac{q}{c}\right)^{j}B_{j}\,.\] (132) \[Z(\beta):=\varphi_{\beta,\rho}(1)=\frac{1}{q}\sum_{1\leq c<q\atop c\notin p{ \mathbb{N}}}\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty} \binom{1-\beta}{j}\left(\frac{q}{c}\right)^{j}B_{j}\,.\] (132) Это \(p\)-адическая \(L\)-функция для характера \(\chi=1\) (_cf._[37], Глава 5, Теорема 5.11) \[Z(\beta)=L_{p}(\beta,1).\] (133) \[Z(\beta)=L_{p}(\beta,1).\] (133) Более того, заметим, что Иваcавская конструкция \(L\)-функций (_cf._[37], Глава 7, Теорема 7.10) даёт формальный степенной ряд \(\frac{1}{2}g(T)\in{\mathbb{Z}}_{p}[[T]]^{\times}\) такой, что (с \(q\) как в (89)) выполняется следующее равенство \[L_{p}(\beta,1)=g\left((1+q)^{\beta}-1\right)/\left(1-(1+q)^{1-\beta}\right)\,, \quad~{}\forall\beta\in D_{p}.\] (134) \[L_{p}(\beta,1)=g\left((1+q)^{\beta}-1\right)/\left(1-(1+q)^{1-\beta}\right)\,, \quad~{}\forall\beta\in D_{p}.\] (134) Так как \(\frac{1}{2}g(T)\in{\mathbb{Z}}_{p}[[T]]^{\times}\) является обратимым (_см._[37] Лемма 7.12), это дает требуемый результат. ∎ Обратите внимание, что \(Z(\beta)\) имеет полюс при \(\beta=1\), с остатком, заданным уравнением \[\frac{1}{q}\sum_{1\leq c<q\atop c\notin p{\mathbb{N}}}1=\frac{\varphi(q)}{q}= \frac{p-1}{p}\,.\] \[\frac{1}{q}\sum_{1\leq c<q\atop c\notin p{\mathbb{N}}}1=\frac{\varphi(q)}{q}= \frac{p-1}{p}\,.\] **Предложение 7.12**: _Когда \(\beta\to 1\), имеем_ \[\lim_{\beta\to 1}Z(\beta)^{-1}Z_{\rho}(\frac{a}{b},\beta)=\left\{\begin{array} []{ll}1&\text{если}\ \frac{a}{b}\in{\mathbb{Z}}\\ 0&\text{иначе.}\end{array}\right.\] (135) Доказательство: Предположим сначала, что \(\frac{a}{b}\notin{\mathbb{Z}}\). Тогда \(\xi=\rho(\zeta_{a/b})\) является ненулевым корнем из единицы, порядок которого \(m>1\) делит \(b\), которое взаимно просто с \(p\) и, следовательно, взаимно просто с \(q\). Используя разложение \({\mathbb{Z}}/bq{\mathbb{Z}}={\mathbb{Z}}/q{\mathbb{Z}}\times{\mathbb{Z}}/b{ \mathbb{Z}}\), мы получаем \[\sum_{1\leq c<bq\atop c\notin p{\mathbb{N}}}\xi^{c}=\varphi(q)\sum_{n\in{ \mathbb{Z}}/b{\mathbb{Z}}}\xi^{n}=0.\] \[\sum_{1\leq c<bq\atop c\notin p{\mathbb{N}}}\xi^{c}=\varphi(q)\sum_{n\in{ \mathbb{Z}}/b{\mathbb{Z}}}\xi^{n}=0.\] Если \(\frac{a}{b}\in{\mathbb{Z}}\), то результат следует из вышесказанного.∎ Обратите внимание, что предел функциональных значений \(Z(\beta)^{-1}Z(\frac{a}{b},\beta)\) при \(\beta\to 1\) не зависит от значений \(\rho\) (т.е. не зависит от выбора \(\sigma\in X_{p}\)). В комплексном случае функциональные значения при \(\beta>1\) задаются формулой (24). В этом случае мы теперь непосредственно проверим, что для \(\beta\in{\mathbb{C}}\), \(\Re(\beta)>1\) функциональные значения определяют \(\rho:{{\mathbb{Q}}^{\rm cyc}}\to{\mathbb{C}}\) как вложение абстрактного циклотомического поля \({{\mathbb{Q}}^{\rm cyc}}\) в \({\mathbb{C}}\). **Лемма 7.13**: \((1)\) _Пусть \(\lambda\in\hat{\mathbb{Z}}^{*}\), \(\lambda\neq\pm 1\). Тогда график умножения на \(\lambda\) в \({\mathbb{Q}}/{\mathbb{Z}}\) является плотным подмножеством \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\)._ \((2)\) _Пусть \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\). Предположим, что \(\theta\notin\{\pm p^{\mathbb{Z}}\}\). Тогда график \(\theta\) плотен в \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\)._ Доказательство: \((1)\) Множество \(G = \{(\alpha, \lambda\alpha) \mid \alpha \in {\mathbb{Q}}/{\mathbb{Z}}\}\) является подгруппой \({\mathbb{R}}/{\mathbb{Z}} \times {\mathbb{R}}/{\mathbb{Z}}\), а его замыкание \(\bar{G}\) также является подгруппой. Если \(G\) не было бы плотным, то существовал бы нетривиальный характер \(\chi\) компактной группы \({\mathbb{R}}/{\mathbb{Z}} \times {\mathbb{R}}/{\mathbb{Z}}\), ядро которого содержит \(\bar{G}\). Таким образом, существовал бы ненулевая пара \((n, m) \in {\mathbb{Z}}^2\), такая что \(n\alpha + m\lambda\alpha \in {\mathbb{Z}}\) для всех \(\alpha \in {\mathbb{Q}}/{\mathbb{Z}}\). Это означало бы, что умножение на \(\lambda \in \hat{\mathbb{Z}}^*\) в группе \({\mathbb{Q}}/{\mathbb{Z}} = {\mathbb{A}}_{{\mathbb{Q}},\,f}/\hat{\mathbb{Z}}\) (\({\mathbb{A}}_{{\mathbb{Q}},\,f}\) - конечные адели) должно выполняться \(n\alpha+m\lambda\alpha \in \hat{\mathbb{Z}}, \quad~{} \forall \alpha \in {\mathbb{A }}_{{\mathbb{Q}},\,f}\). Это означает, что \((n+m\lambda_p)\alpha \in {\mathbb{Z}}_p, \quad~{} \forall \alpha \in {\mathbb{Q }}_p\), и следовательно, \(n+m\lambda_p=0\) для всех простых чисел \(p\). Если \(n/m \notin \{\pm 1\}\), это противоречит тому факту, что \(\lambda \in \hat{\mathbb{Z}}^*\)_то есть_\(\lambda_p \in \hat{\mathbb{Z}}_p^*\) для всех \(p\). \((2)\) Согласно Лемме 8.6, группа \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) является группой автоморфизмов группы \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) в роли аддитивной группы \(\Gamma=\prod^{res}_{\ell\neq p}{\mathbb{Q}}_{\ell}/{\mathbb{Z}}_{\ell}\). Пусть \(\lambda\in G_{p}\) представляет \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\). Тогда тот же самый доказательство, что и в \((1)\), показывает, что если граф \(\theta\) не плотный, то существует ненулевая пара \((n,m)\in{\mathbb{Z}}^{2}\), такая что \(n+m\lambda_{\ell}=0\) для всех простых чисел \(\ell\neq p\). Отсюда следует, что \(-n/m\in\{\pm p^{\mathbb{Z}}\}\) и \(\theta\in\{\pm p^{\mathbb{Z}}\}\).∎ Из Леммы 7.13 следует, что если \(f:\{z\in{\mathbb{C}}\mid|z|=1\}\to{\mathbb{C}}\) - непрерывная не постоянная функция, и \(\rho_{j}:{{\mathbb{Q}}^{\rm cyc}}\to{\mathbb{C}}\), являются инъективными, то имеется равенство вида \[f(\rho_{1}(\zeta_{a/b}))=f(\rho_{2}(\zeta_{a/b}))\,,\quad~{}\forall a/b\in{ \mathbb{Q}}/{\mathbb{Z}}\] (136) translates to: \[\displaystyle f(\rho_{1}(\zeta_{a/b}))=f(\rho_{2}(\zeta_{a/b}))\,,\quad~{}\forall a/b\in{\mathbb{Q}}/{\mathbb{Z}}\] (136) обязательно означает, что \(\rho_{2}=\rho_{1}\) или \(\rho_{2}=\bar{\rho}_{1}\). В последнем случае также получается \[\displaystyle f(\bar{z})=f(z)\,,\quad~{}\forall z,\ |z|=1.\] С учетом уникальности разложения Фурье, такая ситуация не может возникнуть, если \(f(z)=\sum_{{n=1}}^{{\infty}}n^{-\beta}z^{n}\), где \(\Re\mathfrak{e}(\beta)>1\). Затем мы фиксируем целое число \(\beta=1-m=1-k\varphi(q)\), \(k>0\), и изучаем зависимость от \(\rho\) в выражениях (121). Для выбранной пары вложений \(\rho,\rho^{\prime}\), предположим, что \(Z_{\rho}(\frac{a}{b},\beta)=Z_{\rho^{\prime}}(\frac{a}{b},\beta)\) выполняется для всех \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), _т.е._ равенство выполняется для всех дробей с знаменателем \(b\), взаимно простым с \(p\). Из (121) следует, что имеет место равенство (с \({\rm Fr}\) обозначается автоморфизм Фробениуса для \(\widehat{{\mathbb{Q}}_{p}^{\rm ur}}\)) \[\left(1-p^{m-1}{\rm Fr}\right)^{-1}Z_{\rho}\left(\frac{a}{b},\beta\right)=-\frac{b^{m-1}}{m}\sum_{1 \leq c\leq b}\rho\left(\zeta_{a/b}^{c}\right)\,B_{m}\left(\frac{c}{b}\right)\in\widehat{{\mathbb{Q}} _{p}^{\rm ur}}.\] (137) Таким образом мы получаем \[\sum_{1\leq c\leq b}\rho(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})=\sum_{1\leq c \leq b}\rho^{\prime}(\zeta_{a/b}^{c})\,B_{m}(\frac{c}{b})\qquad\forall a/b\in{ ({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (138) Поскольку и \(\rho\) и \(\rho^{\prime}\) являются изоморфизмами группы корней из единицы в \({\mathbb{Q}}^{\rm cyc,p}\) с группой корней из единицы в \({\mathbb{C}}_{p}\) порядка, взаимно простого с \(p\), существует автоморфизм \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\), такой, что \(\rho^{\prime}(\zeta_{a/b})=\rho(\zeta_{\theta(a/b)})\) для всех \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). У нас есть \[ \sum_ {1 \ леюня \ c \ лею \ b} \rho ^ {'} (\zeta_ {а / б} ^ {с}) \, B_ {м} (\фрац {с} {б}) = \sum_ {1 \ лею \ c \ лею \ b} \rho (\zeta_ {\theta (с / б)} ^ {a}) \, B_ {м} (\фрац {с} {б}) = \sum_ {1 \ леюня \ c \ лею \ b} \rho (\zeta_ {а / б} ^ {с}) \, B_ {м} (\див^{-1} (\фрац {с} {б})). \] Используя уникальность преобразования Фурье для конечной группы \({\mathbb{Z}}/b{\mathbb{Z}}\), (138) дает равенство \[B_{m}(\theta^{-1}(\frac{c}{b}))=B_{m}(\frac{c}{b})\qquad\forall \frac{c}{b}\in{({ \mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (139) **Лемма 7.14**. _Пусть \(p>2\) и \(\theta\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}})\). Если \(\theta\in\{\pm 1\}\), то_ \[Z_{\rho}\left(\frac{a}{b},\beta\right)=Z_{\theta\circ\rho}\left(\frac{a}{b},\beta\right)\,,\quad~{} \forall a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}},\ \beta\in D_{p}.\] (140) _Если \(\theta\notin\{\pm 1\}\) и \(\beta=1-m=1-k\varphi(q)\), \(k>0\), то функционалы \(Z_{\rho}(\cdot,\beta)\) и \(Z_{\theta\circ\rho}(\cdot,\beta)\) различны._ Доказательство.: Чтобы доказать (140), мы можем предположить, что \(\theta=-1\)_т.е._ что \(\theta(\zeta_{a/b})=\zeta_{a/b}^{-1}\) для всех \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Тогда у нас есть, с \(\rho^{\prime}=\theta\circ\rho\): \(\rho^{\prime}(\zeta_{a/b}^{c})=\rho(\zeta_{a/b}^{b-c})\). Давайте сначала возьмем \(\beta=1-m=1-k\varphi(q)\). Имеем \[\sum_{1 \leq c \leq b}\rho^{\prime}(\zeta_{a/b}^{c})\,B_{m}\left(\frac{c}{b}\right)=\sum_{0 \leq c \leq b-1}\rho(\zeta_{a/b}^{c})\,B_{m}\left(\frac{b-c}{b}\right)\,.\] Поскольку \(m=k\varphi(q)\) — четное число, полином Бернулли \(B_{m}\) удовлетворяет равенству \[\text{B}_m(1-x)=\text{B}_\text{m}(x)\,,\quad~{}\forall m\in 2{\mathbb{N}}\,.\] (141) (\[\text{141}\]) Таким образом, (140) следует для всех значений \(\beta=1-m=1-k\varphi(q)\). Поскольку эти значения допускают \(0\) как точку сгущения, получается равенство аналитических функций на их области определения \(D_{p}\). Теперь мы предполагаем, что \(\theta\notin\{\pm p^{\mathbb{Z}}\}\). Тогда следует из Леммы 7.13, что график \(\theta\) плотен в \({\mathbb{R}}/{\mathbb{Z}}\times{\mathbb{R}}/{\mathbb{Z}}\). Таким образом, из (139) следует, что \(B_{m}(x)\) является константой, что является противоречием. Остается показать, что для ненулевых степеней \(p^{a}\) числа \(p\) невозможно иметь равенство вида \[B_{m}(x)=B_{m}(p^{a}x-[p^{a}x])\,,\quad~{}\forall x\in[0,1]\] translates to: \[\displaystyle B_{m}(x)=B_{m}(p^{a}x-[p^{a}x])\,,\quad~{}\forall x\in[0,1]\] где \([p^{a}x]\) - это целая часть \(p^{a}x\). На самом деле, это означает, что \(B_{m}(x)-B_{m}(p^{a}x)\) имеет бесконечное количество нулей, следовательно, \(B_{m}(x)=B_{m}(p^{a}x)\), что противоречит. ∎ ### Расширение теории KMS\({}_{\beta}\) до покрытия \({\mathbb{C}}_{p}\) В этом разделе мы показываем, что построение состояний KMS\({}_{\beta}\) \(\varphi_{\beta,\rho}\), для \(\beta \in D_{p}\), естественным образом расширяется на покрытие \({\mathbb{C}}_{p}\), определяемое следующим гомоморфизмом группы \[M=D(1,1^{-})\ni\lambda\mapsto\beta=\ell(\lambda)=\frac{\log_{p}\lambda}{\log_{ p}(1+q)}\in{\mathbb{C}}_{p}\] (142) \[\large M=D(1,1^{-})\ni\lambda\mapsto\beta=\ell(\lambda)=\frac{\log_{p}\lambda}{\log_{ p}(1+q)}\in{\mathbb{C}}_{p}\] (142) где \(M=D(1,1^{-})\) - открытый единичный диск в \({\mathbb{C}}_{p}\) с радиусом \(1\), рассматриваемый как мультипликативная группа. С точностью до нормализующего множителя \(\log_{p}(1+q)\), этот гомоморфизм группы совпадает с определением логарифма Ивасавы и является сюръективным с ядром, являющимся подгруппой корней из единицы порядка \(p\)-степеней (_cf._[32], Теорема p. 257), и он определяет по ограничению взаимно однозначное соответствие. \[ \ell:\{\lambda\in M\mid|\lambda-1|_{p}<p^{-1/(p-1)}\}\stackrel{{ \sim}}{{\to}}D_{p} \] (143) чей обратный элемент определяется отображением \[D_{p}\ni\beta\mapsto\psi(\beta)=(1+q)^{\beta}={\rm exp}(\beta\log_{p}(1+q)).\] (144) (\[D_{p}\in\beta \mapsto \psi(\beta)=(1+q)^{\beta}={\rm exp}(\beta\log_{p}(1+q)).\]) (144) Конструктивно, этот локальный раздел является гомоморфизмом группы, что позволяет рассматривать аддитивную группу \(D_{p}\) как подгруппу \(M\). Мы начинаем с расширения определения функций \(r^{(\beta)}\) как в (98), которые были внедрены в построение автоморфизмов \(\sigma^{(\beta)}\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) (_см._ Предложение 7.3). Для \(r\in{\mathbb{Z}}_{(p)}^{\times}\) выполняется равенство \[i_{p}(r)=\frac{\log_{p}(r)}{\log_{p}(1+q)}\in{\mathbb{Z}}_{p}\] (145) \[i_{p}(r)=\frac{\log_{p}(r)}{\log_{p}(1+q)}\in{\mathbb{Z}}_{p}\] (145) определяет гомоморфизм группы из \({\mathbb{Z}}_{(p)}^{\times}\) в аддитивной группе \({\mathbb{Z}}_{p}\). **Лемма 7.15**. Для \(\beta\in D_{p}\), \(r\in{\mathbb{Z}}_{(p)}^{\times}\) и \(\lambda=(1+q)^{\beta}\) имеет место следующее: \[\langle r\rangle^{\beta}=\lambda^{i_{p}(r)}\,,\ \ r^{(\beta)}=\omega(r)\, \lambda^{i_{p}(r)}.\] (146) \[\langle r\rangle^{\beta}=\lambda^{i_{p}(r)}\,,\ \ r^{(\beta)}=\omega(r)\, \lambda^{i_{p}(r)}.\] (146) Доказательство: У нас есть \(\log_{p}(r)=i_{p}(r)\log_{p}(1+q)\in q{\mathbb{Z}}_{p}\). Таким образом, \(|\beta\log_{p}(r)|_{p}<p^{-1/(p-1)}\) и \[\langle r\rangle^{\beta}={\rm exp}(\beta\log_{p}(r))={\rm exp}(\beta i_{p}(r) \log_{p}(1+q))=(1+q)^{\beta i_{p}(r)}=\lambda^{i_{p}(r)}.\] \[\langle r\rangle^{\beta}={\rm exp}(\beta\log_{p}(r))={\rm exp}(\beta i_{p}(r) \log_{p}(1+q))=(1+q)^{\beta i_{p}(r)}=\lambda^{i_{p}(r)}.\] Второе равенство следует из определения (98).∎ Предложение 7.3 и его доказательство таким образом распространяются от \(D_{p}\) к \(M\). Это означает, что для \(\lambda\in M\) существует единственное автоморфное преобразование \(\sigma[\lambda]\in{\rm Aut}({\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)})\) такое, что \[\sigma[\lambda](\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*})=\omega(b/a)\lambda^{i_{p} (b/a)}\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*}\,,\quad~{}\forall a,b\in I(p),\ \gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (147) \[\sigma[\lambda](\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*})=\omega(b/a)\lambda^{i_{p} (b/a)}\tilde{\mu}_{a}e(\gamma)\mu_{b}^{*}\,,\quad~{}\forall a,b\in I(p),\ \gamma\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}.\] (147) Затем мы расширяем построение линейных форм \(\varphi_{\beta,\rho}\), данное в §7.3. Достаточно расширить определение функций из Леммы 7.6 (которую мы доказали независимой от выбора \(f\neq 0\) кратного \(bq\)). \[Z_{\rho}(\frac{a}{b},\beta):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{\mathbb {N}}}\rho(\zeta_{a/b}^{c})\,\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j= 0}^{\infty}\binom{1-\beta}{j}\left(\frac{f}{c}\right)^{j}B_{j},\qquad\beta\in D _{p}.\] (148) Для определения искомого расширения удобно выразить указанную выше функцию через падиковые \(L\)-функции \(L_{p}(\beta,\chi)\), связанные с кратными символами Дирихле с некоторым примообразным \(f_{\chi}\), взаимно простым с \(p\). По определению, символ Дирихле \(\chi\) является характером мультипликативной группы \(\hat{\mathbb{Z}}^{*}\), и его примообразное \(f_{\chi}\) - это целое число такое, что ядро \(\chi\) совпадает с ядром проекции \(\hat{\mathbb{Z}}^{*}\to({\mathbb{Z}}/f_{\chi}{\mathbb{Z}})^{*}\). Определение \(L_{p}(\beta,\chi)\) аналогично (148) следующим образом \[L_{p}(\beta,\chi):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p\mathbb{N}}\chi( c)\,\frac{\langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1- \beta}{j}\left(\frac{f}{c}\right)^{j}B_{j}\] (149) где \(f\) - это любое кратное числа \(pf_{\chi}\), а \(\chi\) было расширено до периодической функции с периодом \(f_{\chi}\), и исчезает вне множества \(({\mathbb{Z}}/f_{\chi}{\mathbb{Z}})^{*}\). Мы напоминаем, что функция \(L\)-функции \(L_{p}(\beta,\chi)\) тождественно равна нулю, когда характер \(\chi\) нечетный, т.е. когда \(\chi(-1)=-1\) (_см._[37] Замечания стр. 57). Более того, когда \(\chi\) является четным, неприводимым, и его проводник взаимно прост с \(p\), существует аналитическая функция \(H_{\chi}\) на \(M\), такая что (_см._[37] Теорема 7.10) \[ L_{p}(\beta,\chi)=H_{\chi}((1+q)^{\beta})\,,\quad~{}\forall\beta\in D_{p}\,.\] (150) \] \[ L_{p}(\beta,\chi)=H_{\chi}((1+q)^{\beta})\,,\quad~{}\forall\beta\in D_{p}\,.\] (150) \] Расширение функций \(Z_{\rho}(\frac{a}{b},\beta)\) до \(M\) является следствием следующего. **Лемма 7.16****.**: _Для любого \(a/b\in{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) существуют коэффициенты \(c(d,\chi)\in{\mathbb{C}}_{p}\) такие, что_ \[Z_{\rho}(\frac{a}{b},\beta)=\sum_{d|b,\,\chi}c(d,\chi)L_{p}(\beta,\chi)d^{-1} \langle d\rangle^{1-\beta}\prod(1-\chi(\ell)\ell^{-1}\langle\ell\rangle^{1- \beta})\] (151) _где \(d\) изменяется среди делителей \(b\), а для фиксированного \(d\), \(\chi\) изменяется среди множества дирихлеовых символов, чей проводник \(f_{\chi}\) делит \(m=b/d\). Целые числа \(\ell\) - это простые числа, которые делят \(m/f_{\chi}\), но не являются делителями \(f_{\chi}\)._ Доказательство: Пусть \(b\) - целое число, взаимно простое с \(p\), и \(g\in C({\mathbb{Z}}/b{\mathbb{Z}},{\mathbb{C}}_{p})\). Выражение \[Y(g,\beta):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}g(c)\,\frac{ \langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1-\beta}{j}\left (\frac{f}{c}\right)^{j}B_{j},\qquad\beta\in D_{p}\] (152) \[Y(g,\beta):=\frac{1}{f}\sum_{1\leq c<f\atop c\notin p{\mathbb{N}}}g(c)\,\frac{ \langle c\rangle^{1-\beta}}{\beta-1}\sum_{j=0}^{\infty}\binom{1-\beta}{j}\left (\frac{f}{c}\right)^{j}B_{j},\qquad\beta\in D_{p}\] (152) не зависит от выбора кратного \(f\neq 0\) от \(bq\). Пусть \(\chi\) - характер Дирихле (со значениями в \({\mathbb{C}}_{p}\)) с проводником \(f_{\chi}\), а \(m\) - кратное \(f_{\chi}\). Тогда следующее определяет мультипликативное отображение из \({\mathbb{Z}}/m{\mathbb{Z}}\) в \({\mathbb{C}}_{p}\) \[z(\chi,m)(c)=\left\{\begin{array}[]{ll}\chi(c)&\hbox{если}\,c\in({\mathbb{Z}}/m{ \mathbb{Z}})^{*}\\ 0&\hbox{в противном случае.}\end{array}\right.\] (153) Если \(m\) делит \(b\) и заменить \(\chi\) на \(z(\chi,m)\) в (149), то вместо \(L_{p}(\beta,\chi)\) получается функция \[Y(z(\chi,m),\beta)=L_{p}(\beta,\chi)\prod(1-\chi(\ell)\ell^{-1}\langle\ell \rangle^{1-\beta})\] (154) \[Y(z(\chi,m),\beta)=L_p(\beta, \chi)\prod(1-\chi(\ell)\ell^{-1}\langle\ell \rangle^{1-\beta})\] (154) где целые числа \(\ell\) являются простыми числами, которые делят \(m/f_{\chi}\), но не делят \(f_{\chi}\). Затем определим для любого делителя \(d\) числа \(b\) и любой функции \(h\in C({\mathbb{Z}}/m{\mathbb{Z}},{\mathbb{C}}_{p})\), \(m=b/d\), \[e_{d}(h)(a)=\left\{\begin{array}[]{ll}h(a/d)&\hbox{если}\,d|a\\ 0&\hbox{в противном случае.}\end{array}\right.\] Один тогда получает \[Y(e_{d}(h),\beta)=d^{-1}\langle d\rangle^{1-\beta}Y(h,\beta).\] (155) \[Y(e_{d}(h),\beta)=d^{-1}\langle d\rangle^{1-\beta}Y(h,\beta).\] (155) Таким образом, используя (154) и (155), достаточно доказать, что для любой функции \(g\in C({\mathbb{Z}}/b{\mathbb{Z}},{\mathbb{C}}_{p})\) существуют коэффициенты \(c(d,\chi)\in{\mathbb{C}}_{p}\) такие, что \[g(c)=\sum_{d|b,\,\chi}c(d,\chi)e_{d}(z(\chi,b/d)).\] \[g(c)=\sum_{d|b,\,\chi}c(d,\chi)e_{d}(z(\chi,b/d)).\] На самом деле достаточно проверить это для \(g=\delta_{a}\), где \(a\in{\mathbb{Z}}/b{\mathbb{Z}}\). Пусть \(d\) - это наибольший общий делитель \(a\) и \(b\). Имеем \(\delta_{a}=e_{d}(\delta_{c})\), где \(c=a/d\) взаимно прост с \(m=b/d\). Более того, для любого элемента \(c\in({\mathbb{Z}}/m{\mathbb{Z}})^{*}\) имеем \[\delta_{c}(x)=\frac{1}{\varphi(m)}\sum_{\chi,\,f_{\chi}|m}\chi(c)^{-1}z(\chi,m )(x)\,,\quad~{}\forall x\in{\mathbb{Z}}/m{\mathbb{Z}},\] \[\delta_{c}(x)=\frac{1}{\varphi(m)}\sum_{\chi,\,f_{\chi}|m}\chi(c)^{-1}z(\chi,m )(x)\,,\quad~{}\text{для всех } x\in{\mathbb{Z}}/m{\mathbb{Z}},\] которое дает необходимое равенство.∎ Мы таким образом получаем следующее расширение Теоремы 7.11 **Теорема 7.17****.**: _Существует аналитическое семейство функционалов \(\psi_{\lambda,\rho}\), \(\lambda\in M\), на \({\mathcal{H}}_{\mathbb{Z}}^{(p)}\) такое, что_ \(\bullet\) _\(\psi_{\lambda,\rho}(1)=1.\)_ will be translated to: \(\bullet\) _\(\psi_{\lambda,\rho}(1)=1.\)_ \(\bullet\)_\(\psi_{\lambda,\rho}\) удовлетворяет условию КМП_ \[\psi_{\lambda,\rho}(x\sigma[\lambda](y))=\psi_{\lambda,\rho}(y\,x)\,,\quad~{} \forall x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}.\] (156) translates to: \[\psi_{\lambda,\rho}(x\sigma[\lambda](y))=\psi_{\lambda,\rho}(y\,x)\,,\quad~{} \text{для всех } x,y\in{\mathcal{H}}_{{\mathbb{C}}_{p}}^{(p)}.\] (156) \(\bullet\) _Для \(\beta\in D_{p}\) и \(\lambda=(1+q)^{\beta}\) имеем_ \[\psi_{\lambda,\rho}=Z(\beta)^{-1}\varphi_{\beta,\rho}\,.\] \[\psi_{\lambda,\rho}=Z(\beta)^{-1}\varphi_{\beta,\rho}\,.\] Доказательство.: Из (134) следует, что существует аналитическая функция \(z(\lambda)\) от \(\lambda\in M\), такая что \[Z(\beta)^{-1}=(1+q-\lambda)z(\lambda)\,,\ \ \lambda=(1+q)^{\beta}.\] \[ Z(\beta)^{-1}=(1+q-\lambda)z(\lambda)\,,\ \ \lambda=(1+q)^{\beta}. \] Применяя (150), Лемму 7.15 и Лемму 7.16, мы видим, что существует, для \(b\in I(p)\) и \(a/b\notin{\mathbb{Z}}\), аналитическая функция \(H_{a,b}(\lambda)\) от \(\lambda\in M\), такая что \[Z_{\rho}\left(\frac{a}{b},\beta\right)=H_{a,b}(\lambda)\,,\ \ \lambda=(1+q)^{\beta}.\] Это доказывает существование аналитического семейства функционалов \(\psi_{\lambda,\rho}\), удовлетворяющих требуемым условиям. ∎ ## 8. Расширение \(p\)-адической оценки до \({{\mathbb{Q}}^{\rm цик}}\) Для глобального поля \({\mathbb{K}}\) положительной характеристики (т.е. функционального поля, связанного с проективной, несингулярной кривой \(C\) над конечным полем \({\mathbb{F}}_{q}\)), хорошо известно, что пространство оценок максимального абелева расширения \({\mathbb{K}}^{\rm ab}\) над \({\mathbb{K}}\) имеет геометрический смысл. Фактически, для каждого конечного расширения \(E\) \(\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}}\subset{\mathbb{K}}^ {\rm ab}\) пространство \({\rm Val}(E)\) (дискретных) оценок \(E\) превращается в алгебраическую, одномерную схему, непустые открытые множества которой являются дополнениями конечных подмножеств \(F\subset{\rm Val}(E)\). Пучок структур определяется локально пересечением \(\bigcap_{F}R\) оценочных колец внутри \(E\). Затем пространство \({\rm Val}({\mathbb{K}}^{\rm ab})\) является проективным пределом схем \({\rm Val}(E)\), \(E\subset{\mathbb{K}}^{\rm ab}\). Для глобального поля \({\mathbb{K}}={\mathbb{Q}}\) рациональных чисел можно рассмотреть его максимальное абелево расширение \({{\mathbb{Q}}^{\rm cyc}}\) как абстрактное поле (_см._ Определение 8.1) и попытаться следовать похожей идее. Однако в Разделе 9 мы увидим, что пространство \({\rm Val}({{\mathbb{Q}}^{\rm cyc}})\) представляет только грубый аналог, в нулевой характеристике, пространства \({\rm Val}({\mathbb{K}}^{\rm ab})\). В данном разделе разрабатывается предварительный этап представления 5 различных, но эквивалентных описаний пространства \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) расширений \(p\)-адической оценки \({\mathbb{Q}}\) до абстрактного циклотомического поля \({{\mathbb{Q}}^{\rm cyc}}\). Поле \({{\mathbb{Q}}^{\rm cyc}}\) является композицией поля, порожденного корнями из единицы порядка \(p\)-степени, и поля \({\mathbb{Q}}^{\rm cyc,p}\), порожденного корнями из единицы, взаимно простыми с \(p\). Мы описываем канонические изоморфизмы \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) с¹. [ССЫЛКА:1][КОНЕЦ ССЫЛКИ] \((1)\) Пространство последовательностей неприводимых полиномов \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), удовлетворяющих основным условиям полиномов Конвея (_см._ Теорема 8.7). \((2)\) Пространство \(\Sigma_{p}\) взаимно однозначных соответствий моноида \({{\mathcal{M}}{(p)}}=\mu^{(p)}\cup\{0\}\) корней из единицы порядка, взаимнопростых с \(p\), которые коммутируют со своими сопряженными элементами, как в Определении 8.5 (см. Также Предложение 8.8). \((3)\) Пространство \({\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\), где \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) является фиксированным полем под действием автоморфизма Фробениуса (_сравн._ Предложение 8.12). \((4)\) Частное пространства \(X_p\) из Определения 4.3 по действию \({\rm Gal}(\bar{\mathbb{F}}_{p})\) (_см._ Предложение 8.14). \((5)\) Алгебраический спектр фактор-алгебры \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]/J_{p}\), где \(J_{p}\) - остаток от деления по модулю \(p\) циклотомического идеала (_см._ Определение 8.1 и Предложение 8.16). Кстати, мы замечаем, что \((1)\) описывает связь между \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и явным построением алгебраического замыкания \(\bar{\mathbb{F}}_{p}\) над \({\mathbb{F}}_{p}\) с помощью последовательности неприводимых многочленов над \({\mathbb{F}}_{p}\), удовлетворяющих основным условиям полиномов Конвея². Теорема 8.7 утверждает, что отображение, которое сопоставляет оценке \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) последовательность \(\{P_{n}\}\) характеристических многочленов действия (умножения) примитивного корня \(\xi_{\frac{1}{p^{n}-1}}\in{\mathbb{Q}}^{\rm cyc,p}\) на остаточное поле ограничения \(v\) на \({\mathbb{Q}}^{\rm cyc,p}\), определяет биекцию между \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и последовательностями многочленов в \({\mathbb{F}}_{p}[T]\), удовлетворяющих основным условиям полиномов Конвея. [FOOTNOTE:2][ENDFOOTNOTE] (Примечание 2) **Определение 8.1****.**: _Абстрактное циклотоматическое поле \({{\mathbb{Q}}^{\rm cyc}}\) является фактор-кольцом группового кольца \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\) по идеалу \(J\), порожденному idempotents._ \[\pi_{n}=\frac{1}{n}\sum_{j=0}^{n-1}e(\frac{j}{n}),\qquad n\geq 2.\] (157) translates to: \[\pi_{n}=\frac{1}{n}\sum_{j=0}^{n-1}e(\frac{j}{n}),\qquad n\geq 2.\] (157) В общем случае, если мы позволим `$x$` быть выходом функции `$f$` для входа `$y$`: ```math x = f(y) ``` то inversely, функция `$f^{-1}$` является таковой, что ```math y = f^{-1}(x) ``` или в более компактной записи: ```math x = f(y) \iff y = f^{-1}(x) ``` где `$f^{-1}(x)$` является обратной функцией к `$f(x)$`. \[\sigma_{k}(x)=\sum_{j=0}^{k-1}\,x^{j},\] (158) \[\sigma_{k}(x)=\sum_{j=0}^{k-1}\,x^{j},\] (158) затем известно, что \(n\)-ый циклотомический многочлен \(\Phi_{n}(x)\) является НОДом многочленов \(\sigma_{m}(x^{d})\), для \(m>1\), \(m|n\) и \(d=n/m\). Для \(x=e(1/n)\) и \(n=md\) имеем \[ \sigma_{m}(x^{d})=\sum_{j=0}^{m-1}\,e(j/m)=m\,\pi_{m}\in J \] таким образом \(\Phi_{n}(e(1/n))\in J\). Отсюда следует, что гомоморфизм \[\rho_{0}:{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]/J\to{\mathbb{C}}\,,\ \ \rho_{ 0}(e(\gamma))=e^{2\pi i\gamma}\] (159) \[\rho_{0} : {\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]/J \to {\mathbb{C}}\,, \ \ \rho_{ 0}(e(\gamma))=e^{2\pi i\gamma}\] (159) вызывает изоморфизм \({{\mathbb{Q}}^{\rm цик}}\) с подполем \({\mathbb{C}}\), порождаемым корнями из единицы. Используя идентификацию \({\mathbb{Q}}/{\mathbb{Z}}={\mathbb{A}}_{{\mathbb{Q}}}^{f}/\hat{\mathbb{Z}}\), группа \(\hat{\mathbb{Z}}^{*}\) действует автоморфизмами на \({\mathbb{Q}}/{\mathbb{Z}}\) и, следовательно, на групповом кольце \({\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]\). Это действие сохраняет глобально \(n\)-кручение в \({\mathbb{Q}}/{\mathbb{Z}}\) и, следовательно, фиксирует каждую проекцию \(\pi_{n}\). Отсюда следует, что оно глобально инвариантно идеалу \(J\) и, следовательно, индуцирует действие на коэффициентах поля частных \({{\mathbb{Q}}^{\rm cyc}}\). Это действие дает группу Галуа \(G={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\simeq\hat{\mathbb{Z}}^{*}\), которая действует на корнях из единицы так же, как она действует на \({\mathbb{Q}}/{\mathbb{Z}}\). Для каждого простого числа \(p\) выполнено (\(\ell=\) рациональное простое) \[G=\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}={\mathbb{Z}}_{p}^{*}\times\prod_{\ell \neq p}{\mathbb{Z}}_{\ell}^{*}={\mathbb{Z}}_{p}^{*}\times G_{p}.\] (160) \[G=\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}={\mathbb{Z}}_{p}^{*}\times\prod_{\ell \neq p}{\mathbb{Z}}_{\ell}^{*}={\mathbb{Z}}_{p}^{*}\times G_{p}.\] (160) Один поднимает \({\mathbb{Z}}_{p}^{*}\) к подгруппе \({\mathbb{Z}}_{p}^{*}\times 1\subset G\), все компоненты которой равны \(1\) за исключением \(p\). Эта подгруппа действует тривиально на \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). Ее неподвижное подполе \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) является подполем \({{\mathbb{Q}}^{\rm cyc}}\), порожденным над \({\mathbb{Q}}\) группой \(\mu^{(p)}\subset{{\mathbb{Q}}^{\rm cyc}}\) корней из единицы, чей порядок взаимно прост с \(p\). Оно совпадает с _подполем инерции_. \[{{\mathbb{Q}}^{\rm цикл.}}\cap{\mathbb{Q}}_{p}^{\rm ур}\subset{{\mathbb{Q}}^{\rm цикл.}}\] (161) для любого расширения \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) \(p\)-адической оценки до \({{\mathbb{Q}}^{\rm cyc}}\). Более точно, пусть \(({{\mathbb{Q}}^{\rm cyc}})_{v}\) будет завершением \({{\mathbb{Q}}^{\rm cyc}}\) для оценки \(v\). Тогда известно, что составное подполе \({\mathbb{Q}}_{p}\cdot{{\mathbb{Q}}^{\rm cyc}}\subset({{\mathbb{Q}}^{\rm cyc}})_{v}\) является максимальным абелевым расширением \({\mathbb{Q}}_{p}^{\rm ab}\) для \({\mathbb{Q}}_{p}\). Это расширение является составным (см.[34]) \[{\mathbb{Q}}_{p}^{\rm ab}={\mathbb{Q}}_{p}^{\rm ur}\cdot{\mathbb{Q}}_{p^{ \infty}}\] (162) \[{\mathbb{Q}}_{p}^{\rm ab}={\mathbb{Q}}_{p}^{\rm ur}\cdot{\mathbb{Q}}_{p^{ \infty}}\] (162) где \({\mathbb{Q}}_{p}^{\rm ur}\) обозначает максимальное неразветвленное расширение \({\mathbb{Q}}_{p}\), а \({\mathbb{Q}}_{p^{\infty}}\) получается путем добавления ко всему \({\mathbb{Q}}_{p}\) всех корней из единицы порядка \(p\)-степени. Теорема перевода Галуа дает каноническое изоморфизм (по ограничению) групп Галуа. \[{ \rm Gal}({\mathbb{Q}}_{p}^{\rm ab}:{\mathbb{Q}}_{p})\stackrel{{ \sim}}{{\to}}{\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{{\mathbb{Q}}^{\rm cyc}}\cap{ \mathbb{Q}}_{p}),\qquad\alpha\mapsto\alpha|_{{\mathbb{Q}}^{\rm cyc}}.\] (163) \[{ \rm Gal}({\mathbb{Q}}_{p}^{\rm ab}:{\mathbb{Q}}_{p})\stackrel{{ \sim}}{{\to}}{\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{{\mathbb{Q}}^{\rm cyc}}\cap{ \mathbb{Q}}_{p}),\qquad\alpha\mapsto\alpha|_{{\mathbb{Q}}^{\rm cyc}}.\] (163) Подполе _декомпозиционного_ поля: \({{\mathbb{Q}}^{\rm cyc}}\cap{\mathbb{Q}}_{p}\) не зависит от выбора оценки \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\), так как \(G\) абелев и действует транзитивно на \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\), более точно, имеет место следующий классический результат **Предложение 8.2**. \((1)\) _Группа \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) является группой автоморфизмов группы \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\)._ \((2)\) _Инерционное подполе \({\mathbb{Q}}^{\rm cyc,p}\) представляет собой неподвижное подполе \({\mathbb{Z}}_{p}^{*}\subset G\), и его группа Галуа канонически изоморфна \(G_{p}\), действующему на \(\mu^{(p)}\subset{\mathbb{Q}}^{\rm cyc,p}\) так же, как она действует на \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\)._ \((3)\) _Пусть \(f_{p}\in G_{p}\) будет элементом \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) со всеми компонентами, равными \(p\). Тогда соответствующий автоморфизм \({\rm Fr}\in{\rm Aut}({\mathbb{Q}}^{\rm cyc,p})\) является единственным автоморфизмом, который действует как \(x\mapsto x^{p}\) на мультипликативной группе \(\mu^{(p)}\subset{\mathbb{Q}}^{\rm cyc,p}\)._ \((4)\) _Подполе с фиксированным полем \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) относительно \({\rm Fr}\) является подполем разложения \({{\mathbb{Q}}^{\rm cyc}}\cap{\mathbb{Q}}_{p}\)._ \((5)\) _Группа \(G={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\) действует транзитивно на \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) с изотропией \({\mathbb{Z}}_{p}^{*}\times f_{p}^{\hat{\mathbb{Z}}}\), где \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\) - замыкание \(f_{p}^{\mathbb{Z}}\)._ Доказательство: \((1)\) Пусть \(\Gamma\) является дискретной группой, определенной как \({(\mathbb{Q}/\mathbb{Z})}^{(p)}\). Дуальная группа Понтрягина \(\hat{\Gamma}\) представляет собой произведение \(\prod_{\ell\neq p}\mathbb{Z}_{\ell}\). Мы утверждаем, что группа автоморфизмов \(\Gamma\) является \[{\rm Aut}(\Gamma)=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\,\,.\] (164) Действительно, имеем \(\Gamma=\prod^{res}_{\ell\neq p}{\mathbb{Q}}_{\ell}/{\mathbb{Z}}_{\ell}\), откуда двойственное к \(\Gamma\) равно \(\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}\). Это компактное кольцо, содержащее \({\mathbb{Z}}\) в качестве плотного подкольца. Таким образом, автоморфизм \(\theta\) аддитивной группы характеризуется присваиванием \(a=\theta(1)\) и представляется умножением на \(a\). Обратимость показывает, что \(a\in\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\). Это доказывает (164). \((2)\) Под изоморфизмом (163) группа Галуа \({\rm Gal}({\mathbb{Q}}_{p^{\infty}}:{\mathbb{Q}}_{p})\simeq{\mathbb{Z}}_{p}^{*}\) становится подгруппой \({\mathbb{Z}}_{p}^{*}\times 1\subset G\). Подполе, оставшееся неподвижным для этой подгруппы, это \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) и является инерционным подполем \({{\mathbb{Q}}^{\rm cyc}}\). Факторгруппа \(G/{\mathbb{Z}}_{p}^{*}\) канонически изоморфна \(G_{p}\). \((3)\) Под изоморфизмом \({\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q}})=G_{p}\) действие \({\rm Fr}\) на \(\mu^{(p)}\) соответствует умножению на \(p\) в \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\). \((4)\) Галуа-группа \({\rm Gal}({\mathbb{Q}}_{p}^{\rm ur}:{\mathbb{Q}}_{p})\simeq\hat{\mathbb{Z}}\) топологически порождается автоморфизмом Фробениуса \({\rm Fr}_{p}\), действие которого на корнях единиц порядка, взаимно простых с \(p\), задано как \({\rm Fr}_{p}(\xi)=\xi^{p}\). При изоморфизме (163) этот автоморфизм ограничивается до автоморфизма \({\rm Fr}\in{\rm Aut}({\mathbb{Q}}^{\rm cyc,p})\). Обратите внимание, что поля \({\mathbb{Q}}^{\rm cyc,p}\) и \({\mathbb{Q}}_{p}\) являются линейно независимыми над их пересечением. \[K={\mathbb{Q}}^{\rm cyc,p}\cap{\mathbb{Q}}_{p}={{\mathbb{Q}}^{\rm cyc}}\cap{ \mathbb{Q}}_{p}\,.\] (165) \[K={\mathbb{Q}}^{\rm cyc,p}\cap{\mathbb{Q}}_{p}={{\mathbb{Q}}^{\rm cyc}}\cap{ \mathbb{Q}}_{p}\,.\] (165) Затем, теорема перевода в теории Галуа показывает, что, ограничиваясь до \({\mathbb{Q}}^{\rm cyc,p}\), имеется изоморфизм \[\text{{Гал}}({\mathbb{Q}}_{p}^{\text{{ур}}}:{\mathbb{Q}}_{p})\stackrel{{ \sim}}{{\to}}\text{{Гал}}({\mathbb{Q}}^{\text{{цик.}},p}:K),\qquad\text{{Fr}}_{p}\mapsto{ \text{{Fr}}}.\] Это показывает, что \(K\) является фиксированным подполем \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}^{\rm cyc,p}\) относительно \({\rm Fr}\). \((5)\) Хорошо известно, что группа Галуа действует транзитивно на расширениях оценки. Более того, подгруппа изотропии является подгруппой группы Галуа, соответствующей подполю разложения, и поэтому может быть представлена как \({\mathbb{Z}}_{p}^{*}\times f_{p}^{\hat{\mathbb{Z}}}\). ∎ **Следствие 8.3**: _Естественное отображение \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\to{\rm Val}_{p}({\mathbb{Q}}^{\rm cyc, p})\) , заданное ограничением значений функций показателей, является соответствующим и биективным._ Доказательство: Карта ограничений является эквивариантной для действия \(G\) на обоих пространствах, эти действия являются транзитивными и имеют одну и ту же группу изотропии, поэтому карта ограничений является биекцией.∎ Фактически, стоит явно указать единственное расширение оценки \(v\in{\rm Val}_{p}({\mathbb{Q}}^{\rm cyc,p})\) до \({{\mathbb{Q}}^{\rm cyc}}\). Последнее поле получается путем присоединения к \({\mathbb{Q}}^{\rm cyc,p}\) примитивных корней из единицы порядка степени \(p\), _т.е._ решения \(z\) уравнения вида \[z^{(p-1)p^{m-1}}+z^{(p-2)p^{m-1}}+\ldots+1=0.\] Один записывает \(z=1+\pi\) и обнаруживает, что уравнение, выполняемое для \(\pi\), является уравнением типа Эйзенштейна, где константный член равен \(p\) и сводится к \(\pi^{\varphi(n)}=0\), по модулю \(p\). Это показывает, что \[v(\pi)=\frac{v(p)}{\varphi(n)}\,,\ \ \varphi(n)=(p-1)p^{m-1}.\] \[v(\pi)=\frac{v(p)}{\varphi(n)}\,,\ \ \varphi(n)=(p-1)p^{m-1}.\] Затем, оценка \(v\), нормализованная так, чтобы \(v(p)=1\), единственным образом расширяется на элементы расширения \({\mathbb{Q}}^{\rm cyc,p}[z]\) путем установки \[v(a_{0}+a_{1}\pi+\ldots+a_{\varphi(n)-1}\pi^{\varphi(n)-1})=\inf\{v(a_{j})+ \frac{j}{\varphi(n)}\}.\] (166) \[v(a_{0}+a_{1}\pi+\ldots+a_{\varphi(n)-1}\pi^{\varphi(n)-1})=\inf\{v(a_{j})+ \frac{j}{\varphi(n)}\}.\] (166) **Замечание 8.4**. Подполе разложения \({\mathbb{Q}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\) является бесконечным расширением \({\mathbb{Q}}\) и содержит, например, \(\sqrt{n}\) для \(n\) - квадратичного остатка по модулю \(p\). Его группа Галуа \({\rm Gal}({\mathbb{Q}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\) является фактором группы \(G_{p}\) по замыканию группы степеней \(f_{p}\) и является компактной группой, которая содержит для каждого простого числа \(\ell\neq p\) циклическую группу порядка \(\ell-1\), возникающую из кручения \({\mathbb{Z}}_{\ell}^{*}\). **Определение 8.5****.**: _Пусть \({{\mathcal{M}}{(p)}}=\{0\}\cup\mu^{(p)}\) - это моноид, полученный путем добавления нулевого элемента к мультипликативной группе \(\mu^{(p)}\). Мы обозначаем \(\Sigma_{p}\) множество биекций \(s:{{\mathcal{M}}{(p)}}\to{{\mathcal{M}}{(p)}}\), которые коммутируют со своими сопряженными \(R\circ s\circ R^{-1}\) при поворотах \(R\) элементами \(\mu^{(p)}\), и удовлетворяют соотношениям: \(s(0)=1\), \(s^{p}=s\circ s\circ\ldots\circ s=id\)._ Отображения \(s\) кодируют сложение \(1\) на \({{\mathcal{M}}{(p)}}\), когда мультипликативная структура моноида \({{\mathcal{M}}{(p)}}\) обогащается сложной структурой, превращая его в поле характеристики \(p\) (т.е. алгебраическое замыкание \({\mathbb{F}}_{p}\)). Обратите внимание, что, используя дистрибутивность, сложение \(1\) кодирует полную аддитивную структуру (_см._[12]). **Лемма 8.6**: _Группа \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) действует транзитивно на \(\Sigma_{p}\) с изотропией \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\)._ Доказательство. Мы проверяем, что \(G_{p}\) действует транзитивно на \(\Sigma_{p}\). Пусть \(s_{j}\in\Sigma_{p}\), для \(j=1,2\), и пусть \({\mathbb{K}}(s_{j})\) - две соответствующие поля на \({{\mathcal{M}}{(p)}}\). Затем два поля \({\mathbb{K}}(s_{j})\) являются алгебраическими замыканиями \({\mathbb{F}}_{p}\) и, следовательно, они изоморфны. Пусть \(\theta:{\mathbb{K}}(s_{1})\to{\mathbb{K}}(s_{2})\) - такой изоморфизм. По построению \(\theta\) является автоморфизмом мультипликативной группы \(\mu^{(p)}\) и переносит операцию \(s_{1}\) сложения \(1\) в \({\mathbb{K}}(s_{1})\) в операцию \(s_{2}\) сложения \(1\) в \({\mathbb{K}}(s_{2})\). Используя теорию Галуа, получаем, что изотропия любого \(s\in\Sigma_{p}\) является замыканием группы степеней \(f_{p}\), _т.е._ подгруппой \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\).∎ Мы готовы объявить основной результат этого раздела. **Теорема 8.7****.**: _Элемент \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) полностью характеризуется последовательностью полиномов \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\) степени \(n\geq 1\), таких что_ \(\bullet\) _каждый \(P_{n}(T)\) является моническим и неразложимым._ \(\bullet\)_\(T\in{\mathbb{F}}_{p}[T]/(P_{n}(T))\) является генератором мультипликативной группы поля частного._ \(\bullet\) _Для любого целого числа \(m|n\) и для \(d=(p^{n}-1)/(p^{m}-1)\), \(P_{m}(T^{d})\) является кратным \(P_{n}(T)\)._ Доказательство. Первый шаг в доказательстве состоит в построении естественного отображения \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\ni v\mapsto s_{v}\in\Sigma_{p}\). Мы знаем, что \({\mathbb{Q}}_{p}\subset({{\mathbb{Q}}^{\rm cyc}})_{v}\) и что \(\mu^{(p)}\cup\{0\}\subset{{\mathbb{Q}}^{\rm cyc}}\), поэтому мы рассматриваем кольцо оценки \({\mathbb{Z}}_{p}^{\rm ur}\subset({{\mathbb{Q}}^{\rm cyc}})_{v}\) расширения \({\mathbb{Q}}_{p}^{\rm ur}\). Оно содержит \({\mathbb{Z}}_{p}\) и \(\mu^{(p)}\). Обратите внимание, что кольцо, порожденное \({\mathbb{Z}}\) и \(\mu^{(p)}\), является кольцом целых чисел подполя \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\) порожденного над \({\mathbb{Q}}\) с помощью \(\mu^{(p)}\). Имеется диаграмма вложений. \({({{\mathbb{Q}}^{\rm cyc}})_{v}}\)\({{{\mathbb{Q}}^{\rm cyc}}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)oo\({\bar{\mathbb{F}}_{p}}\)\({{\mathbb{Z}}_{p}^{\rm ur}\ignorespaces\ignorespaces\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)OO\({\epsilon}\)oo\({{\mathbb{Z}}_{p}^{\rm ur}\cap{{\mathbb{Q}}^{\rm cyc}}\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)ООoo\({\mu^{(p)}\cup\{0\}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)оо\({{\mathbb{F}}_{p}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)ОО\({{\mathbb{Z}}_{p}\ignorespaces\ignorespaces\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)\({\epsilon}\)ооОО\({{\mathbb{Z}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)ООoo\({\tau({\mathbb{F}}_{p})\ignorespaces\ignorespaces\ignorespaces \ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}\)ООoo (173) где \(\tau:{\mathbb{F}}_{p}\to{\mathbb{Z}}_{p}\) является подъемом Тейхмюллера. Обратите внимание, что \(\tau({\mathbb{F}}_{p})\subset{\mathbb{Z}}_{p}\cap{{\mathbb{Q}}^{\rm цикл}}\), поскольку этот подъем состоит из корней из единицы (порядка \(p-1\)). В середине строки вышеуказанной диаграммы композитное отображение \(\epsilon\) от \(\mu^{(p)}\cup\{0\}\) до \(\bar{\mathbb{F}}_{p}\) является изоморфизмом мультипликативных моноидов. Действительно, подъем Тейхмюллера \(\bar{\mathbb{F}}_{p}\ni x\mapsto\tau(x)\in{\mathbb{Z}}_{p}^{\rm ur}\) дает обратное отображение. Поскольку \(\bar{\mathbb{F}}_{p}\) является полем, его аддитивную структуру можно транспортировать с помощью \(\epsilon\), и таким образом получается единственный элемент \(s_{v}\in\Sigma_{p}\). **Предложение 8.8**: _Отображение \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\ni v\mapsto s_{v}\in\Sigma_{p}\) является биекцией и является сопряжением для действия \(G_{p}={\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q}})\)._ Доказательство: Действие \(G_{p}\) на подмножество \(\mu^{(p)}\) описано в Лемме 8.6. Это показывает, что отображение \(v\mapsto s_{v}\) является эквивариантным. Поскольку оба пространства \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и \(\Sigma_{p}\) являются гомогенными пространствами над \(G_{p}\) с одинаковыми группами изотропии \(p^{\hat{\mathbb{Z}}}\subset G_{p}\), как следует из Лемм 8.2 и 8.6, отображение \(v\mapsto s_{v}\) является биективным. ∎ Мы можем создать конкретную конструкцию оценки \(v\), связанной с отображением \(s_{v}\). Сначала определяется \(v\) на подполе \({\mathbb{Q}}^{\rm cyc,p}\subset{{\mathbb{Q}}^{\rm cyc}}\). Достаточно определить оценку \(v\) для элементов вида \[x = \sum n_{j}\xi_{j}\,,\ \ n_{j}\in{\mathbb{Z}}\,,\ \ \xi_{j}\in\mu^{(p)} \subset{{\mathbb{Q}}^{\rm цик}}.\] Пусть \(K=\bar{\mathbb{F}}_{p}\) будет алгебраическим замыканием \({\mathbb{F}}_{p}\), полученным, оснащая мультипликативный моноид \(\mu^{(p)}\cup\{0\}\) с добавлением, связанным с \(s_{v}\). Затем имеется \[v(x)=w_{p}\left(\sum n_{j}\tau(\xi_{j})\right)\] (174) can be translated to Russian as: \[v(x)=w_{p}\left(\sum n_{j}\tau(\xi_{j})\right)\] (174) где \( w_{p} \) - это \( p \)-адическая оценка в кольце Витта \({\mathbb{W}}_{p^{\infty}}(K)\), а \( \tau \) - это поднятие Тейхмюллера. Наконец, поскольку поле \({{\mathbb{Q}}^{\rm cyc}}\) является составным из подполей \({\mathbb{Q}}^{\rm cyc,p}\) и фиксированного поля действия \( G_{p} \subset \hat{\mathbb{Z}}^{*}={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q }}) \), которое порождено корнями единицы порядка \( p \)-степени, можно использовать (166), чтобы уникально расширить оценку \( v \) до \({{\mathbb{Q}}^{\rm cyc}}\). [РИСУНОК:S8.F1][КОНЕЦРИСУНКА] Мы готовы завершить доказательство Теоремы 8.7, _т.е._ мы доказываем, что: **Лемма 8.9**: _Элемент \(s\in\Sigma_{p}\) полностью определяется последовательностью \(P_{n}(T)\) полиномов из \({\mathbb{F}}_{p}[T]\), удовлетворяющих условиям Конвея, как в Теореме 8.7._ Доказательство. Пусть \(s\in\Sigma_{p}\). Для каждого \(n\in{\mathbb{N}}\) пусть \({\mathbb{K}}_{n}(s)\) будет соответствующей полевой структурой на объединении \(\{0\}\cup\mu^{(p)}(n)\), где \(\mu^{(p)}(n)\) - группа корней из единицы порядка \(p^{n}-1\) в \({{\mathbb{Q}}^{\rm cyc}}\) порожденная \(\xi=e(\frac{1}{p^{n}-1})\). Векторное пространство \({\mathbb{K}}_{n}(s)\) над \({\mathbb{F}}_{p}\) имеет размерность \(n\), так как его мощность равна \(p^{n}\). Канонический порождающий элемент \(\xi\) для \(\mu^{(p)}(n)\) действует на векторном пространстве \({\mathbb{K}}_{n}(s)\) умножением \(M_{\xi}\). Пусть \(P_{n}(T)\) - его характеристический многочлен, то есть определитель \(P_{n}(T)=\det(T-M_{\xi})\). Это монический многочлен степени \(n\) с коэффициентами в \({\mathbb{F}}_{p}\). В поле \({\mathbb{K}}_{n}(s)\) имеем \(P_{n}(\xi)=0\), так как \(M_{\xi}\) удовлетворяет своему характеристическому уравнению. Таким образом, мы получаем гомоморфизм алгебр \(\rho:{\mathbb{F}}_{p}[T]/(P_{n}(T))\to{\mathbb{K}}_{n}(s)\), который отображает \(T\mapsto\xi\). Он сюръективен, так как любой ненулевой элемент \({\mathbb{K}}_{n}(s)\) является степенью \(\xi\). Так как \(P_{n}(T)\) имеет степень \(n\), две алгебры имеют одинаковую размерность над \({\mathbb{F}}_{p}\), и, следовательно, \(\rho\) является изоморфизмом. Отсюда следует, что \(P_{n}(T)\) неприводим над \({\mathbb{F}}_{p}\). Второе свойство \(P_{n}(T)\) также следует, так как \(\xi\) является порождающим элементом мультипликативной группы. Теперь пусть \(m|n\) - делитель \(n\). Тогда \(r=p^{m}-1\) делит \(k=p^{n}-1\), и группа \(\mu^{(p)}(m)\) является подгруппой \(\mu^{(p)}(n)\). Таким образом, имеется включение полей \({\mathbb{K}}_{m}(s)\subset{\mathbb{K}}_{n}(s)\), где канонический порождающий элемент \(\xi_{m}=e(\frac{1}{p^{m}-1})\) из \({\mathbb{K}}_{m}(s)\) переходит в \(\xi_{n}^{d}\), где \(\xi_{n}\) - канонический порождающий элемент \(\xi_{n}=e(\frac{1}{p^{n}-1})\) из \({\mathbb{K}}_{n}(s)\), и \(d=(p^{n}-1)/(p^{m}-1)\). Имеем \(P_{m}(\xi_{m})=0\), и следовательно, \(P_{m}(\xi_{n}^{d})=0\), так что, используя вышеуказанный изоморфизм \(\rho\), получаем, что многочлен \(P_{m}(T^{d})\) является кратным многочлена \(P_{n}(T)\). Обратно, задавая последовательность \(P_{n}(T)\) полиномов, удовлетворяющих условиям теоремы, строится алгебраическое замыкание \(\bar{\mathbb{F}}_{p}\) и изоморфизм \[\bar{\mathbb{F}}_{p}^{*}\stackrel{{ j}}{{\longrightarrow}}\mu^{(p)}\] translates to: \[\bar{\mathbb{F}}_{p}^{*}\stackrel{{ j}}{{\longrightarrow}}\mu^{(p)}\] как следует из условия, для каждого \(n\), \({\mathbb{K}}_{n}={\mathbb{F}}_{p}[T]/(P_{n}(T))\), и получается индуктивная система, использующая для \(m|n\) гомоморфизм поля, который отправляет генератор \(T_{m}\) \({\mathbb{K}}_{m}\) в \(T_{n}^{d}\), где \(d=(p^{n}-1)/(p^{m}-1)\). Индуктивный предел \({\mathbb{K}}=\varinjlim{\mathbb{K}}_{n}\) является алгебраическим замыканием \(\bar{\mathbb{F}}_{p}\) над \({\mathbb{F}}_{p}\), и отображение \(T_{n}\mapsto e^{2\pi i/k}\), где \(k=p^{n}-1\), определяет изоморфизм \(j\) между \(\bar{\mathbb{F}}_{p}^{*}\) и \(\mu^{(p)}\). Заметим, что данная конструкция имеет смысл также для \(n=1\), и что первый полином имеет степень один и, следовательно, выбирает конкретный генератор мультипликативной группы \({\mathbb{F}}_{p}\). Проверим, что последовательность полиномов, ассоциированная с парой \((\bar{\mathbb{F}}_{p},j)\), это последовательность \(P_{n}(T)\). Таким образом, существует полное соответствие между элементами \(s\in\Sigma_{p}\) и последовательностями полиномов, удовлетворяющих условиям Конвея в теореме. ∎ Для более ясного представления вышеприведенной карты от \(\Sigma_{p}\) к последовательностям полиномов мы вводим "следовой инвариант" элемента \(s\in\Sigma_{p}\). Мы продолжаем обозначать \({\mathbb{K}}_{n}(s)\) структуру поля на объединении \(\{0\}\cup\mu^{(p)}(n)\), где \(\mu^{(p)}(n)\) - это группа корней из единиц, порожденная \(\xi=e(\frac{1}{p^{n}-1})\). В частности, \({\mathbb{K}}_{1}(s)\) - это поле, уникально изоморфное \({\mathbb{F}}_{p}\). Пусть \(\eta\in\mu^{(p)}\), тогда орбита \({\mathcal{O}}=\{{\rm Fr}^{k}(\eta)\mid k\in{\mathbb{N}}\}\) отображения \(x\mapsto{\rm Fr}(x)=x^{p}\) является конечным множеством, пусть \(|{\mathcal{O}}|\) - его мощность. Затем следующая сумма \[\text{{tr}}_{s}({\mathcal{O}})=\sum_{{\mathcal{O}}}\eta\] (175) вычисляемое в любом \({\mathbb{K}}_{n}(s)\), для \(|{\mathcal{O}}||n\) одного и того же и определяет элемент из \({\mathbb{K}}_{1}(s)={\mathbb{F}}_{p}\). **Определение 8.10**. Пусть \({\mathbb{O}}(p)\) - это пространство орбит отображения \(x\mapsto{\rm Fr}(x)=x^{p}\), действующего на \(\mu^{(p)}\). Пусть \(s\in\Sigma_{p}\). Мы называем это отображение \[ {\rm tr}_{s}:{\mathbb{O}}(p)\to{\mathbb{F}}_{p}\,,\ \ {\mathcal{O}}\mapsto{\rm tr }_{s}({\mathcal{O}})\ (176) \] _следовой инвариант \(s\)._ След-невырожденный характеризует \(s\), как показано следующим утверждением. **Утверждение 8.11**: _Пусть \(s\in\Sigma_{p}\). Тогда для каждого \(n\in{\mathbb{N}}\) полином \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), связанный с \(s\) по Лемме 8.9, задается_ \[P_{n}(T)=T^{n}+\sum_{k=1}^{n-1}(-1)^{k}\sigma_{k}T^{n-k}\] (177) \[P_{n}(T)=T^{n}+\sum_{k=1}^{n-1}(-1)^{k}\sigma_{k}T^{n-k}\] (177) для \[\sigma_{k}=\sum_{{\mathcal{O}}\subset D_{k}}{\rm tr}_{s}({\mathcal{O}}),\] (178) \[\sigma_{k}=\sum_{{\mathcal{O}}\subset D_{k}}{\rm tr}_{s}({\mathcal{O}}),\] (178) _где \(D_{k}\subset{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) - это множество дробей \(\frac{a}{p^{n}-1}\), где \(1\leq a\leq p^{n}-1\), а цифры \(a\) в системе счисления \(p\) состоят только из нулей, кроме \(k\) из них, которые равны \(1\)._ Доказательство.: В поле \({\mathbb{K}}_{n}(s)\) \(n\) корней полинома \(P_{n}(T)\) являются элементами \(e(\frac{p^{j}}{p^{n}-1})\), для \(j=0,\ldots,n-1\). Для каждого \(k=1,\ldots,n\), множество произведений \(k\) различных корней является множеством элементов вида \[e\left(\sum_{j\in Y}\frac{p^{j}}{p^{n}-1}\right)\,,\ \ Y\subset\{0,1,\ldots,n- 1\}\,,\ |Y|=k.\] translates to: \[e\left(\sum_{j\in Y}\frac{p^{j}}{p^{n}-1}\right)\,,\ \ Y\subset\{0,1,\ldots,n- 1\}\,,\ |Y|=k.\] Таким образом, получаем, что \(k\)-я симметричная функция \(\sigma_{k}\) корней \(P_{n}(T)\) задается суммой (178) по орбитам \({\mathcal{O}}\), удовлетворяющим заданному условию \({\mathcal{O}}\subset D_{k}\).∎ Мы сейчас приведем третье эквивалентное описание пространства \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Напомним, что подполе разложения \({\mathbb{Q}}_{p}\cap{{\mathbb{Q}}^{\rm cyc}}\) не зависит от выбора \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и равно \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\), принадлежащее \({{\mathbb{Q}}^{\rm cyc}}\). **Предложение 8.12**: _Отображение_ \[\beta:{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\to{\mbox{Hom}}({{\mathbb{Q}}^{ \rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p}),\qquad\beta(v)=\beta_{v}:{{\mathbb{Q}}^ {\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}_{p}\] \[\beta:{\rm Val}_{p}({{\mathbb{Q}}^{\rm цик}})\to{\mbox{Hom}}({{\mathbb{Q}}^{ \rm цик,p}_{\rm Fr}},{\mathbb{Q}}_{p}),\qquad\beta(v)=\beta_{v}:{{\mathbb{Q}}^ {\rm цик,p}_{\rm Fr}}\subset{\mathbb{Q}}_{p}\] _где включение полей \(\beta_{v}\), определенное в (165), определяет каноническое и экивариантное отображение множеств._ Доказательство: Заметим, что включение \(\beta_{v}: {{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\subset{\mathbb{Q}}_{p}\) зависит от выбора оценки \(v\). Для этого имеем \(\beta_{v}\in{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) и отображение \(v\mapsto\beta_{v}\) является сопряженным для действия \(G_{p}/f_{p}^{\hat{\mathbb{Z}}}\) на \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и на пространстве \({\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) при \[{Hom}({{\mathbb{Q}}^{cyc,p}_{Fr}},{\mathbb{Q}}_{p})\ni\beta \mapsto\beta\circ\gamma\,,\quad~{}\forall\gamma\in G_{p}={Gal}({\mathbb{Q}}^{cyc,p}:{\mathbb{Q}}).\] (179) Поскольку для обоих пространств действие \(G_{p}/f_{p}^{\hat{\mathbb{Z}}}\) является свободным и транзитивным, следует, что отображение \(\beta\) является биекцией. ∎ Мы позволяем \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) быть групповым кольцом \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), и позволяем \({\rm Fr}\in{\rm Aut}({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}])\) быть автоморфизмом Фробениуса, заданным естественной линеаризацией группового автоморфизма \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), умножением на \(p\) (_см._ Утверждение 2.4). Естественное кольцевое гомоморфное \[\delta:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Q}}^{\rm cyc ,p}\] (180) \[\delta:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Q}}^{\rm цикл ,p}\] (180) является смежным для действия \({\rm Fr}\), его образ является подкольцом целых чисел \({\mathbb{Q}}^{\rm cyc,p}\), в то время как ядро описывается пересечением множеств \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\) и \(J\), где \(J\) является идеалом из Определения 8.1. Алгебра \({\mathbb{F}}_{p}\) \[\mathbb{Z}[(\mathbb{Q}/\mathbb{Z})^{(p)}]\otimes_{\mathbb{Z}}\mathbb{F}_{p}=\mathbb{F}_{p}[(\mathbb{Q}/\mathbb{Z})^{(p)}]\] (181) идеально, поскольку группа \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\) является уникальной \(p\)-делимой. Ограничиваясь на неподвижные точки \({\rm Fr}\) и композицией с отображением остатков \(\epsilon:{\mathbb{Z}}_{p}\to{\mathbb{F}}_{p}\), получается отображение \[{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\to{\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr},{\mathbb{ F}}_{p}),\quad\alpha\mapsto{\rm res}(\alpha)=\epsilon\circ\alpha\circ\delta.\] (182) Обратите внимание, что элементы \({\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr},{ \mathbb{F}}_{p})\) являются конечно-поддерживаемыми отображениями из \({\mathbb{O}}(p)\) в \({\mathbb{F}}_{p}\), таким образом их можно поднять до элементов \({\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\). Получается \[{\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}={\mathbb{Z}}[{( {\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\otimes_{\mathbb{Z}}{\mathbb{F}}_{p}.\] \[\mathbb{F}_{p}[{(\mathbb{Q}/\mathbb{Z})^{(p)}}]^{\rm Fr}=\mathbb{Z}[{(\mathbb{Q}/\mathbb{Z})^{(p)}}]^{\rm Fr}\otimes_{\mathbb{Z}}\mathbb{F}_{p}.\] Далее показываем, что отображение res, как в (182), является инъективным. **Утверждение 8.13.**: _Пусть \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Обозначим через \(s_{v}\in\Sigma_{p}\) и \(\beta_{v}:{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\to{\mathbb{Q}}_{p}\) соответствующие элементы, как в Лемме 8.8 и Утверждении 8.12. Тогда инвариант отображения следа \(s_{v}\) имеет следующее описание_. \[\text{tr}_{s_{v}}=\text{res}(\beta_{v}).\] (183) _Отображение \({\rm res}\) в форме (182) является инъективным._ Доказательство: Аддитивная структура \(s_{v}\) на \({{\mathcal{M}}{(p)}}=\{0\}\cup\mu^{(p)}\) такая же, как и у полевых остатков завершения \({\mathbb{Q}}^{\rm cyc,p}\) для ограничения \(v\). Следовательно, на каждой орбите \({\mathcal{O}}\) действия \({\rm Fr}\) на \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), сумма \({\rm tr}_{s_{v}}({\mathcal{O}})\) совпадает с остатком. \[\epsilon(\beta_{v}(u))\,,\ \ u=\sum_{\mathcal{O}}\xi\in{{\mathbb{Q}}^{\rm cyc, p}_{\rm Fr}}.\] translates to: \[\epsilon(\beta_{v}(u))\,,\ \ u=\sum_{\mathcal{O}}\xi\in{{\mathbb{Q}}^{\rm цикл, p}_{\rm Фр}}.\] Так как \(u=\delta(w)\), где \(w=\sum_{\mathcal{O}}\xi\in{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{ \rm Fr}\), получаем (183). Затем, из Утверждения 8.11 следует, что отображение \({\rm res}\) инъективно.∎ Мы теперь кратко объясним, как можно восстановить \(\alpha\in{\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}},{\mathbb{Q}}_{p})\) из его остатка \({\rm res}(\alpha)\), используя функтор Витта \({\mathbb{W}}_{p^{\infty}}\). Если \(\varsigma\in{\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] ^{\rm Fr},{\mathbb{F}}_{p})\), то функтор Витта \({\mathbb{W}}_{p^{\infty}}\) порождает гомоморфизм. \[{\mathbb{W}}_{p^{\infty}}(\varsigma)\in{\mbox{Hom}}({\mathbb{W}}_{p^{\infty}}( {\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}),{\mathbb{Z}}_{ p}).\] (184) translates to: \[\mathbb{W}_{p^{\infty}}(\varsigma) \in \text{Hom}(\mathbb{W}_{p^{\infty}}(\mathbb{F}_{p}[{(\mathbb{Q}/\mathbb{Z}})^{(p)}}]^{Fr}), \mathbb{Z}_{p}).\] (184) Если \(\varsigma={\rm res}(\alpha)\), можно восстановить \(\alpha\) напрямую, используя \({\mathbb{W}}_{p^{\infty}}(\varsigma)\). Это дает прямое доказательство инъективности отображения \({\rm res}\). Действительно, для орбиты \({\mathcal{O}}\) действия \({\rm Fr}\) на \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), элемент (\(\tau=\) подъем Тайхмюллера) \[\nu({\mathcal{O}})=\sum_{\mathcal{O}}\tau(\upsilon)\in{\mathbb{W}}_{p^{\infty} }({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}])\] would be translated to: \[\nu({\mathcal{O}})=\sum_{\mathcal{O}}\tau(\upsilon)\in{\mathbb{W}}_{p^{\infty} }({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}])\] (Note that the translation remains the same, as it is in a mathematical form and does not require any changes in the language.) зафиксировано Фробениусом, _т.е._ \(\nu({\mathcal{O}})\in{\mathbb{W}}_{p^{\infty}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr})\). Затем видно, что \[\alpha\left(\sum_{\mathcal{O}}\upsilon\right)={\mathbb{W}}_{p^{\infty}}( \varsigma)(\nu({\mathcal{O}}))\,.\] (185) \[\alpha\left(\sum_{\mathcal{O}}\upsilon\right)={\mathbb{W}}_{p^{\infty}}( \varsigma)(\nu({\mathcal{O}}))\,.\] (185) Мы завершаем этот раздел, представляя связь между \(\Sigma_{p}={\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и пространством \(X_{p}\) всех инъективных гомоморфизмов группы \(\sigma:\bar{\mathbb{F}}_{p}^{\times}\to({{\mathbb{Q}}^{\rm cyc}})^{\times}\) (_см._ Определение 4.3). Мы напоминаем, что группа Галуа \({\rm Aut}(\bar{\mathbb{F}}_{p})\) является замыканием \(f_{p}^{\hat{\mathbb{Z}}}\), группы, порожденной Фробениусом \(f_{p}\). **Утверждение 8.14.**: _Пусть \(\bar{\mathbb{F}}_{p}\) - фиксированное алгебраическое замыкание \({\mathbb{F}}_{p}\). Тогда_ \((1)\)_\(G_{p}\) действует свободно и транзитивно на \(X_{p}\). \((2)\) _Частное от \(X_{p}\) по \(f_{p}^{\hat{\mathbb{Z}}}\) изоморфно \(\Sigma_{p}={\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\)._ Доказательство: Пусть \(\sigma\in X_{p}\). Областью значений \(\sigma\) является группа \(\mu^{(p)}\) всех корней из единицы в \({{\mathbb{Q}}^{\rm cyc}}\) порядка, взаимно простого с \(p\). Таким образом, для пары \(\sigma_{j}\in X_{p}\), \(j=1,2\), имеем \(\sigma_{1}\circ\sigma_{2}^{-1}\in{\rm Aut}({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}} )=G_{p}\). Это доказывает первое утверждение. Для любого изоморфизма \(\sigma:\bar{\mathbb{F}}_{p}^{*}\stackrel{{}}{{\longrightarrow}}({{ \mathbb{Q}}^{\rm cyc}})^{\times}\) мультипликативной группы алгебраического замыкания \(\bar{\mathbb{F}}_{p}\) с группой \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), следующее определяет элемент \(s\in\Sigma_{p}\), \[s(x)=\sigma(\sigma^{-1}(x)+1)\,,\quad~{}\forall x\neq-1\,,\ s(-1)=0.\] (186) \[s(x)=\sigma(\sigma^{-1}(x)+1)\,,\quad~{}\forall x\neq-1\,,\ s(-1)=0.\] (186) Все элементы \(\Sigma_{p}\) возникают таким образом. Легко видеть, что две пары \((\bar{\mathbb{F}}_{p},\sigma_{j})\), \(j=1,2\), у которых соответствующие \(s_{j}\in\Sigma_{p}\) равны, связаны автоморфизмом \(\theta\in{\rm Aut}(\bar{\mathbb{F}}_{p})\)_т.е._\(\sigma_{2}=\sigma_{1}\circ\theta\). Таким образом, следует второе утверждение.∎ Предложение 8.12 предлагает более подходящее эквивалентное описание \(X_{p}\) с использованием выбранного алгебраического замыкания \(\bar{\mathbb{Q}}_{p}\) поля \(p\)-адических чисел и его завершения \({\mathbb{C}}_{p}\). **Следствие 8.15****.**: _Отображение_ \[i:X_{p}\to{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p}),\qquad\sigma \mapsto\tau\circ\sigma^{-1}\\] (187) \[i:X_{p}\to{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p}),\qquad\sigma \mapsto\tau\circ\sigma^{-1}\\] (187) _где \(\sigma^{-1}\) составляет композицию с Teichmüller lift, чтобы определить полевой гомоморфизм из \({\mathbb{Q}}^{\rm cyc,p}\) в \({\mathbb{C}}_{p}\), является взаимно-однозначным отображением множеств._ _Каноническая сюръекция \(X_{p}\to\Sigma_{p}\) в утверждении 8.14\((2)\) является картой ограничения_ \[\mbox{Hom}(\mathbb{Q}^{\rm cyc,p},\mathbb{C}_{p})\to\mbox{Hom}({\mathbb{Q}}^{\rm cyc,p}_{\rm Fr},{\mathbb{Q}}_{p}).\] (188) Доказательство. Пусть \(\sigma\in X_{p}\), тогда \(\sigma^{-1}:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to\bar{\mathbb{F}}_{p}^{\times}\) в сочетании с подъемом Тейхмюллера \(\tau:\bar{\mathbb{F}}_{p}^{\times}\to{\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^ {\rm ur}}}\subset{\mathbb{C}}_{p}\) расширяется до единственного гомоморфизма \(i(\sigma)\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\). Отображение \(i\) удовлетворяет действию \(G_{p}\) на \(X_{p}\) в соответствии с Предложением 8.14 и на \({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\) путем композиции с элементами \(G_{p}={\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q}})\). Поскольку оба действия являются свободными и транзитивными, \(i\) является биекцией. Для любого \(\gamma\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\), область значений \(\gamma\) является подполем максимального бесграничного расширения \({\mathbb{Q}}_{p}^{\rm ur}\subset{\mathbb{C}}_{p}\), порождённой над \({\mathbb{Q}}\) корнями из единицы порядка, не кратного \(p\). По построению имеем \(\gamma\circ{\rm Fr}={\rm Fr}_{p}\circ\gamma\). Таким образом, образ \(\gamma({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}})\) содержится в фиксированном подполе \({\mathbb{Q}}_{p}\) для действия \({\rm Fr}_{p}\) на \({\mathbb{Q}}_{p}^{\rm ur}\). Это показывает, что отображение ограничения (188) определено корректно. Для \(j=1,2\) пусть \(\gamma_{j}\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\), тогда \(\gamma_{2}^{-1}\circ\gamma_{1}\in{\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{\mathbb{Q }})\) и этот автоморфизм фиксирует \({{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\) точечно тогда и только тогда, когда ограничения \(\gamma_{j}|_{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}}\) равны. Поскольку \({\rm Gal}({\mathbb{Q}}^{\rm cyc,p}:{{\mathbb{Q}}^{\rm cyc,p}_{\rm Fr}})\) топологически порождается \({\rm Fr}\), это происходит тогда и только тогда, когда \(\gamma_{j}\) совпадают в факторгруппе \(X_{p}\) по \(f_{p}^{\hat{\mathbb{Z}}}\). ∎ Мы реализуем гомоморфизм \(\delta:{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\to{\mathbb{Q}}^{\rm cyc ,p}\) из (180) для ассоциации элемента \(\rho\in{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\) его остатком \[{\rm res}(\rho)=\epsilon\circ\rho\circ\delta\in{\mbox{Hom}}({\mathbb{F}}_{p}[{ ({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}],\bar{\mathbb{F}}_{p}).\] (189) \[{\rm res}(\rho)=\epsilon\circ\rho\circ\delta\in{\mbox{Hom}}({\mathbb{F}}_{p}[{ ({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}],\bar{\mathbb{F}}_{p}).\] (189) Образ \(\delta\) - это кольцо целых чисел \({\mathbb{Q}}^{\rm cyc,p}\), таким образом образ \(\rho\circ\delta\) в \({\mathbb{C}}_{p}\) содержится в \({\mathcal{O}}_{\widehat{{\mathbb{Q}}_{p}^{\rm ur}}}\), и составной \(\epsilon\circ\rho\circ\delta\) определён. Более того, так как \(\text{Ker}(\delta)=J\cap{\mathbb{Z}}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]\), следовательно \(\text{Ker}({\rm res}(\rho))\) содержит идеал \(J_{p}\) редукции \(\text{Ker}(\delta)\) по модулю \(p\). **Предложение 8.16**. _Пусть \({{\mathcal{A}}}\) - это фактор-алгебра \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]/J_{p}\). Тогда_ \((1)\) _Карта_ \[{\rm res}:{\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\to{\mbox{Hom }}({{\mathcal{A}}},\bar{\mathbb{F}}_{p}),\qquad{\rm res}(\rho)=\epsilon\circ \rho\circ\delta\] (190) _является биекцией множеств._ \((2)\) _Алгебраический спектр \({\rm Spec\,}({{\mathcal{A}}})\) в каноническом сопоставлении с множеством \(\Sigma_{p}\)._ \((3)\) _Каноническое сюръективное отображение \(X_{p}\to\Sigma_{p}\) из Предложения 8.14\((2)\) соответствует естественному отображению_ \[\text{{Hom}}({\mathcal{A}},\bar{\mathbb{F}}_{p})\to\text{{Spec}}({\mathcal{A}}).\] (191) Доказательство: \((1)\) Для любого целого числа \(m\), взаимно простого с \(p\), идеал \(J_{p}\) содержит проекцию (_см._ Определение 8.1) \(\pi_{m}=\frac{1}{m}\sum_{j=0}^{m-1}e(\frac{j}{m})\). Таким образом, элемент \(\rho\in{\mbox{Hom}}({{\mathcal{A}}},\bar{\mathbb{F}}_{p})\) задается гомоморфизмом групп \(\rho:{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\to\bar{\mathbb{F}}_{p}^{\times}\) таким, что (для \(m>1\) взаимно простого с \(p\)) \(\sum_{j=0}^{m-1}\rho(e(\frac{j}{m}))=0\). Заметим, что это равенство выполняется тогда и только тогда, когда \(\rho\) инъективно, и следовательно, при ограничении на конечноуровневые подгруппы в проективном пределе \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\), оно биективно. Таким образом, \((1)\) следует из первого утверждения Следствия 8.15. \((2)\) Рассмотрим конечное поле \({\mathbb{F}}_{p^{n}}\). Два генератора мультипликативной группы \({\mathbb{F}}_{p^{n}}^{\times}\) имеют одинаковый характеристический полином тогда и только тогда, когда они сопряжены при действии группы Галуа \(\text{Gal}({\mathbb{F}}_{p^{n}}:{\mathbb{F}}_{p})\). Это показывает, что кардинальность множества \(I_{n}\) неприводимых примитивных полиномов степени \(n\) над \({\mathbb{F}}_{p}\) равна \(\varphi(p^{n}-1)/n\), где \(\varphi\) - функция Эйлера. Каждый из этих полиномов \(P(X)\) делит сокращение модуля \(p\) циклотомического полинома \(\Phi_{p^{n}-1}(X)\), отсюда получается, что, при модуло \(p\), имеет место следующее равенство \[\Phi_{p^{n}-1}(X)=\prod_{I_{n}}P(X)\] (192) \[\Phi_{p^{n}-1}(X)=\prod_{I_{n}}P(X)\] (192) так как степени полиномов совпадают и правая часть делит левую. Кроме того, у нас также имеется следующее уравнение: \[\Phi_{p^{n}-1}\left(e\left(\frac{1}{p^{n}-1}\right)\right)\in J_{p}\,.\] Это определяет каноническое изоморфизм \[\mathcal{A}_n=\mathbb{F}_p[\mu^{(p)}(n)]/(J_p\cap\mathbb{F}_p[\mu^{(p)}(n)])\to\prod_{I_n}\mathbb{F}_{p^n}\] (193) и, следовательно, каноническое биективное отображение множеств \({\rm Spec\,}({{\mathcal{A}}}_{n})\to I_{n}\). Поскольку \({{\mathcal{A}}}\) является индуктивным пределом \({{\mathcal{A}}}_{n}\), \({\rm Spec\,}({{\mathcal{A}}})\) является проективным пределом \(I_{n}\), _т. е._ пространством последовательностей многочленов Конвея, как в Теореме 8.7. Это пространство находится в канонической биекции с \(\Sigma_{p}\). \( (3) \) следует из доказательства \( (2) \). ∎ Ограничение на неподвижные точки автоморфизма Фробениуса \({\rm Fr}\in{\rm Aut}({{\mathcal{A}}})\) не меняет алгебраический спектр как множество, поэтому мы получаем каноническое взаимно однозначное отображение множеств \[{\rm Spec\,}({{\mathcal{A}}})\stackrel{{\sim}}{{\to}}{\rm Spec\,}( {{\mathcal{A}}}^{\rm Fr}).\] (194) \[{\rm Spec\,}({{\mathcal{A}}})\stackrel{{\sim}}{{\to}}{\rm Spec\,}( {{\mathcal{A}}}^{\rm Fr}).\] (194) Наконец, мы характеризуем образ отображения \({\rm res}\) как в (182). **Следствие 8.17****.**: _Пусть \(\varsigma\in{\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}] ^{\rm Fr},{\mathbb{F}}_{p})\). Тогда \(\varsigma\) принадлежит образу отображения \({\rm res}\) как в (182), если и только если \(\text{Ker}(\varsigma)\) содержит \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\cap J_{p}\)._ Доказательство.: Используя (194) и Proposition 8.16, \((2)\), у нас есть естественные взаимно-однозначные отображения множеств. \[\Sigma_{p}\simeq{\rm Spec\,}({{\mathcal{A}}})\simeq{\rm Spec\,}({{\mathcal{A}} }^{\rm Fr})\simeq{\mbox{Hom}}({{\mathcal{A}}}^{\rm Fr},{\mathbb{F}}_{p}).\] translates to: \[\Sigma_{p} \simeq {\rm Spec\,}({{\mathcal{A}}}) \simeq {\rm Spec\,}({{\mathcal{A}} }^{\rm Fr}) \simeq {\mbox{Hom}}({{\mathcal{A}}}^{\rm Fr},{\mathbb{F}}_{p}).\] Затем следует заметить, что элементы \({\mbox{Hom}}({{\mathcal{A}}}^{\rm Fr},{\mathbb{F}}_{p})\) являются элементами \({\mbox{Hom}}({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr},{ \mathbb{F}}_{p})\), ядро которых содержит \({\mathbb{F}}_{p}[{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}]^{\rm Fr}\cap J_{p}\).∎ ## 9. Проблема базовой точки и "кривая" для глобального поля \({\mathbb{Q}}\) В этом разделе мы сравниваем пространство \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) расширений \(p\)-адической оценки до \({{\mathbb{Q}}^{\rm cyc}}\) (изучено в разделе 8) с фиброй над простым числом \(p\) пространства \(Y\), которое представляет собой аналог кривой, играющей фундаментальную роль в доказательстве римановой гипотезы A. Вейля для функциональных полей. Наши результаты показывают, что для каждого места \(v\in\Sigma({\mathbb{Q}})\) существует естественная модель \(Y_{v}\) для фибры над \(v\) и вложение этой модели в некоммутативное пространство \(X({\mathbb{C}}_{v})\), которое является \(v\)-адическим аватаром пространства аделиевых классов \({\mathbb{H}}_{\mathbb{Q}}={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}\). Мы будем обозначать \({\mathbb{K}}\) глобальным полем. Для обоснования наших конструкций мы сначала напомним несколько соответствующих фактов, верных для функциональных полей. ### Аделева интерпретация петлевой группоиды \(\Pi_{1}^{\rm ab}(X)^{\prime}\) для функциональных полей В этом подразделе мы предполагаем, что \({\mathbb{K}}\) является функциональным полем. Мы позволяем \({\mathbb{F}}_{q}\subset{\mathbb{K}}\) быть полем констант. Пусть \(\bar{\mathbb{K}}\) будет фиксированным разделимым замыканием \({\mathbb{K}}\), а \({\mathbb{K}}^{\rm ab}\subset\bar{\mathbb{K}}\) будет максимальным абелевым расширением \({\mathbb{K}}\). Обозначим \(\bar{\mathbb{F}}_{q}\) алгебраическое замыкание конечного поля \({\mathbb{F}}_{q}\) внутри \({\mathbb{K}}^{\rm ab}\). Основным результатом, справедливым для функциональных полей, является то, что для каждого конечного расширения полей \(E\) из \(\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}}\) пространство (дискретных) оценок \({\rm Val}(E)\) наследует структуру алгебраической одномерной схемы \(X_{E}\), непустые открытые множества которой являются дополнениями к конечным подмножествам, а структурный пучок определен путем рассмотрения пересечения кольцев оценок внутри \(E\). Более точно, \({\rm Val}(E)\) совпадает с множеством (замкнутых) точек уникальной проективной, гладкой алгебраической кривой \(X_{E}\) с функциональным полем \(E\). Мы напоминаем (в сравнении [21], следствие 6.12), что категория носительных, проективных алгебраических кривых и доминантных морфизмов эквивалентна категории функциональных полей размерности один над \(\bar{\mathbb{F}}_{q}\). Таким образом, каждому \({\mathbb{K}}^{\rm ab}=\varinjlim_{E}E\) соответствует (единственным образом) проективный предел \(X^{\rm ab}=\varprojlim_{E}X_{E}\), являющийся абелевым покрытием \(X^{\rm ab}\to X\) невырожденной проективной кривой \(X\) над \({\mathbb{F}}_{q}\) с функциональным полем \({\mathbb{K}}\). Ограничивая оценки, также получается естественное отображение проекции. \[\pi:X^{\rm ab}={\rm Val}({\mathbb{K}}^{\rm ab})\to\Sigma({\mathbb{K}})\] translates to: \[\pi:X^{\rm ab}={\rm Val}({\mathbb{K}}^{\rm ab})\rightarrow\Sigma({\mathbb{K}})\] на пространство \(\Sigma({\mathbb{K}})\) оценок \({\mathbb{K}}\). Таким образом, в случае функционального поля получается геометрическая интерпретация для естественной фибрации, связанной с пространством оценок расширения поля \({\mathbb{K}}^{\rm ab}\supset{\mathbb{K}}\). В [13] мы предоставили аделево описание группоида петли \(\Pi_{1}^{\rm ab}(X)^{\prime}\) абелева накрытия \(X^{\rm ab}\to X\). Мы напоминаем, что аделевое пространство классов \({\mathbb{A}}_{\mathbb{K}}/{\mathbb{K}}^{*}\) любого глобального поля \({\mathbb{K}}\) имеет естественную структуру гиперкольца \({\mathbb{H}}_{\mathbb{K}}\) (_см._[13]) и что простые элементы \(P({\mathbb{H}}_{\mathbb{K}})\) этого гиперкольца определяют группоид. Единицы этого группоида образуют множество \(\Sigma({\mathbb{K}})\) местностей \({\mathbb{K}}\), а отображения источников и целей совпадают с отображением \[\text{s:P({\mathbb{H}}_{\mathbb{K}})}\rightarrow\Sigma({\mathbb{K}})\] который ассоциирует с простым элементом \({\mathbb{H}}_{\mathbb{K}}\) главный простой идеал \({\mathbb{H}}_{\mathbb{K}}\) который он порождает (и, следовательно, соответствующее место). Когда \({\mathbb{K}}\) является функциональным полем, группоид \(P({\mathbb{H}}_{\mathbb{K}})\) канонически изоморфен петлевому группоиду \(\Pi_{1}^{\rm ab}(X)^{\prime}\) абелевого покрытия \(X^{\rm ab}\to X\), и изоморфизм согласован с соответствующими действиями абелевой группы Вейля \({\mathcal{W}}^{\rm ab}\) (_т.е._ подгруппы элементов из \({\rm Gal}({\mathbb{K}}^{\rm ab}:{\mathbb{K}})\), ограничение которых на \(\bar{\mathbb{F}}_{q}\) является целевой степенью Фробениуса), и классом идеалов \(C_{\mathbb{K}}={\mathbb{A}}_{\mathbb{K}}^{*}/{\mathbb{K}}^{*}\). Следовательно, в качестве группового действия на множестве, действие \({\mathcal{W}}^{\rm ab}\) на \({\rm Val}({\mathbb{K}}^{\rm ab})\) изоморфно действию группы классов идель \(C_{\mathbb{K}}\) на \(P({\mathbb{H}}_{\mathbb{K}})\). Другими словами, выбрав теоретическое множество \(\xi\) проекции \[\pi\;:\;{\rm Val}({\mathbb{K}}^{\rm ab})\to\Sigma({\mathbb{K}})\,,\ \ \pi(v)=v |_{\mathbb{K}},\] (195) \[\pi\;:\;{\rm Val}({\mathbb{K}}^{\rm ab})\to\Sigma({\mathbb{K}})\,,\ \ \pi(v)=v |_{\mathbb{K}},\] (195) получается экивариантное сюрьективное отображение между множеством \(P({\mathbb{H}}_{\mathbb{K}})\) и \(Val({\mathbb{K}}^{\rm ab})\), зависящее, однако, важным образом от выбора базовой точки \(\xi(w)\) для каждого места \(w\in\Sigma({\mathbb{K}})\). Эта зависимость не позволяет перенести алгебраическую геометрическую структуру \(X^{\rm ab}\) на \(P({\mathbb{H}}_{\mathbb{K}})\), и также показывает, что адельное пространство \(P({\mathbb{H}}_{\mathbb{K}})\) не несет информацию о кривой \(X^{\rm ab}\) только в терминах множества с групповым действием. ### Волокно над конечным местом поля \({\mathbb{Q}}\) Теперь обратимся к глобальному полю \({\mathbb{K}}={\mathbb{Q}}\). Естественной отправной точкой для построения замены покрытия \(X^{\rm ab}\) в этом случае числового поля является рассмотрение максимального абелева расширения \({\mathbb{Q}}\), _i.e._ циклотомического поля \({{\mathbb{Q}}^{\rm cyc}}\) как аналога \({\mathbb{K}}^{\rm ab}\). Затем, пространство \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) расширений \(p\)-адической оценки до \({{\mathbb{Q}}^{\rm cyc}}\) представляется первым кандидатом на аналог фибры, над конечным местоположением, абелевого покрытия \(X^{\rm ab}\to X\). Таким образом, первым шагом является сравнение \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и фибры \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) фибрации \(s:P({\mathbb{H}}_{\mathbb{Q}})\to\Sigma({\mathbb{Q}})\) над рациональным простым числом \(p\in\Sigma({\mathbb{Q}})\). На уровне множеств с групповыми действиями данный процесс показывает, что \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) еще не является правильной фиброй. Следующее обсуждение указывает на то, что следует рассмотреть вместо этого общую область пространства главного ряда с базой \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и группой структуры связного компактного однопрямого \(S\), определение которого дано в Предложении 9.2. Тогда, естественным построением фибры является отображаемый тор \(Y_{p}\) действия Фробениуса на пространстве \(X_{p}\) Определения 4.3. **Утверждение 9.1**. Пусть \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) - это волокно группоида \(P({\mathbb{H}}_{\mathbb{Q}})\) над нерасширяющимся рациональным простым числом \(p\in\Sigma_{\mathbb{Q}}\). Тогда выполняются следующие результаты. \((1)\) _Группа идельных классов \(C_{\mathbb{Q}}={\mathbb{A}}^{*}_{\mathbb{Q}}/{\mathbb{Q}}^{*}\) действует транзитивно на \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\). Изотропная группа любого элемента \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) является кокомпактной подгруппой \(W_{p}={\mathbb{Q}}_{p}^{*}\subset C_{\mathbb{Q}}\) классов идельных чисел \((j_{v})\) таких, что \(j_{v}=1\), \(\forall v\neq p\)._ \((2)\) _В рамках теории поля классов изоморфизм_ \[{\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\simeq C_{\mathbb{Q}}/D_{ \mathbb{Q}}\,,\ \ D_{\mathbb{Q}}=\text{связная компонента}\;1,\] (196) \(C_{\mathbb{Q}}\) _действует транзитивно на \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) и изотропная группа любого элемента \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) это_ \[I_{p}={\mathbb{Z}}_{p}^{*}\times H\times{\mathbb{R}}_{+}^{*}\subset\hat{ \mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}=C_{\mathbb{Q}}.\] (197) \[I_{p}={\mathbb{Z}}_{p}^{*}\times H\times{\mathbb{R}}_{+}^{*}\subset\hat{ \mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}=C_{\mathbb{Q}}.\] (197) \(H\subset G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) _является замкнутой подгруппой \(p^{\hat{\mathbb{Z}}}\subset G_{p}\), порожденной \(p\) в \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\)._ Доказательство: (1) следует из Теоремы 7.10 из [13]. (2) следует из Леммы 8.2. ∎ Обратите внимание, что если \({\mathbb{K}}\) - функциональное поле и \(v\) - оценка \({\mathbb{K}}^{\rm ab}\), расширяющая оценку \(w\) \({\mathbb{K}}\), то любой \(g\in{\mathcal{W}}^{\rm ab}\), принадлежащий подгруппе локальной Вейловой группы \({\mathcal{W}}^{\rm ab}_{w}\subset{\mathcal{W}}^{\rm ab}\) и такой, что \(g(v)=v\). Это связано с тем, что ограничение \(g\) до автоморфизма \(\bar{\mathbb{F}}_{q}\) является целой степенью Фробениуса. Когда \({\mathbb{K}}={\mathbb{Q}}\), группа изотропии оценки \(v\) вместо этого больше, чем локальная группа Вейля \(W_{p}\). Разница определяется наличием частного \(I_{p}/W_{p}\) из группы изотропии \(I_{p}\) по локальной группе Вейля \(W_{p}={\mathbb{Q}}_{p}^{*}={\mathbb{Z}}_{p}^{*}\times(\tilde{p})^{\mathbb{Z}}\). Здесь \(\tilde{p}\) представлен идеальным элементом, все компоненты которого равны \(1\), кроме места \(p\), где оно равно \(p^{-1}\). Умножая на главный идеаль \(p\), получаем ту же самую классу как элемента в \(\hat{\mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}\), который равен \(p\) везде, кроме места \(p\), где он равен \(1\). Таким образом, его образ в \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) равен \(p\). Факторгруппа \[I_{p}/W_{p}=(H\times{\mathbb{R}}_{+}^{*})/(\tilde{p})^{\mathbb{Z}}\simeq(\hat{ \mathbb{Z}}\times{\mathbb{R}})/{\mathbb{Z}}=S\] (198) \[I_{p}/W_{p}=(H\times{\mathbb{R}}_{+}^{*})/(\tilde{p})^{\mathbb{Z}}\simeq(\hat{ \mathbb{Z}}\times{\mathbb{R}})/{\mathbb{Z}}=S\] (198) является компактным связным соленоидом, который описан в следующем Предложении 9.2. Присутствие связной части \(S\) обусловлено тем, что связная компонента тождества в группе идельных классов действует тривиально на уровне Галуа на \({{\mathbb{Q}}^{\rm cyc}}\). **Предложение 9.2**: _Группа \(S\) компактна и связна и канонически изоморфна проективному пределу компактных групп \({\mathbb{R}}/n{\mathbb{Z}}\), при условии делимости меток \(n\)._ Доказательство. Рассмотрим сначала фактор \[S_{n}=(({\mathbb{Z}}/n{\mathbb{Z}})\times{\mathbb{R}})/{\mathbb{Z}}\] \[S_{n}=(({\mathbb{Z}}/n{\mathbb{Z}})\times{\mathbb{R}})/{\mathbb{Z}}\] проективного предела \(S\), где \({\mathbb{Z}}\) действует по диагонали, _т. е._ элементом \((1,1)\), на \(({\mathbb{Z}}/n{\mathbb{Z}})\times{\mathbb{R}}\). Имеется естественное отображение \(p_{n}:S_{n}\to{\mathbb{R}}/n{\mathbb{Z}}\), заданное \[p_{n}(j,s)=s-j\,,\quad~{}\text{для всех}\ s\in{\mathbb{R}},\ j\in{\mathbb{Z}}/n{\mathbb {Z}},\] где одно рассматривает \({\mathbb{Z}}/n{\mathbb{Z}}\) как подгруппу \({\mathbb{R}}/n{\mathbb{Z}}\). Отображение \(p_{n}\) является изоморфизмом групп. Когда \(n\) делит \(m\), подгруппа \(m{\mathbb{Z}}\subset{\mathbb{Z}}\) содержится в \(n{\mathbb{Z}}\subset{\mathbb{Z}}\) и это соответствует проекции \({\mathbb{Z}}/m{\mathbb{Z}}\to{\mathbb{Z}}/n{\mathbb{Z}}\). Под изоморфизма \({\mathbb{R}}/m{\mathbb{Z}}\to{\mathbb{R}}/n{\mathbb{Z}}\), это соответствует проекции \({\mathbb{R}}/m{\mathbb{Z}}\to{\mathbb{R}}/n{\mathbb{Z}}\). Таким образом, проективная система, определяющая \(S\), изоморфна проективной системе проекций \({\mathbb{R}}/m{\mathbb{Z}}\to{\mathbb{R}}/n{\mathbb{Z}}\), и проективные пределы изоморфны.∎ Далее, мы описываем общую конструкцию картографического тора, которая дает результат, когда применяется к группам \[X=G_{p}\,,\ \ Z=G_{p}/p^{\hat{\mathbb{Z}}},\] (199) \[X=G_p\,,\ \ Z=G_p/p^{\hat{\mathbb{Z}}},\] (199) волокно \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) гроиды \(P({\mathbb{H}}_{\mathbb{Q}})\) над конечным, рациональным простым числом \(p\in\Sigma({\mathbb{Q}})\). **Предложение 9.3****.**: _Пусть \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) - группа автоморфизмов мультипликативной группы \(\mu^{(p)}\) из корней из единицы в \({{\mathbb{Q}}^{\rm cyc}}\) порядка, не являющихся делителями числа \(p\), и пусть \(f_{p}\in G_{p}\) - элемент \(\xi\mapsto\xi^{p}\). Пусть действие группы \(G_{p}\) на компактном пространстве \(X\) является свободным и транзитивным. Пусть \(Y\) будет фактор-пространством_ \[Y=\left(X\times(0,1)\right)/\sigma^{\mathbb{Z}},\] (200) translates to: \[Y=\frac{X\times(0,1)}{\sigma^{\mathbb{Z}}},\] (200) _где \(\sigma^{\mathbb{Z}}\) действует на произведение \(X\times(0,1)\) следующим образом_ \[\sigma(x,\rho)=(f_{p}x,\rho^{p})\,,\quad~{}\forall x\in X,\ \rho\in(0,1).\] (201) \[\sigma(x,\rho)=(f_{p}x,\rho^{p})\,,\quad~{}\forall x\in X,\ \rho\in(0,1).\] (201) _Затем выполняются следующие результаты._ \((1)\) _Пространство \(Y\) компактно и является \(S\)-главным расслоением над фактор-пространством \(Z\) от \(X\) по \(f_{p}^{\hat{\mathbb{Z}}}\subset G_{p}\), где \(S\) является группой соленоида из Предложения 9.2._ \((2)\) _Пусть \(X\) и \(Z\) будут такими, как в (199), тогда \(Y\) канонически изоморфно волокну \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\)._ Доказательство.: \((1)\) Сначала рассмотрим действие \({\mathbb{Z}}\) на открытый интервал \((0,1)\), заданное как \(\rho\mapsto\rho^{p}\). Рассмотрим отображение \(\psi:(0,1)\to{\mathbb{R}}\), заданное \[\psi(\rho)=\log(-\log(\rho))\,,\quad~{}\forall\rho\in(0,1).\] (202) \[\psi(\rho)=\log(-\log(\rho))\,,\quad~{}\forall\rho\in(0,1).\] (202) Один имеет \[\psi(\rho^{p})=\log(-\log(\rho^{p}))=\log(-p\log(\rho))=\log(-\log(\rho))+\log (p)=\psi(\rho)+\log(p)\] которое показывает, что действие \({\mathbb{Z}}\) на \((0,1)\), заданное как \(\rho\mapsto\rho^{p}\), изоморфно действию \({\mathbb{Z}}\) на \({\mathbb{R}}\), заданному как сдвиг на \(\log(p)\). По конструкции \(G_{p}=\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}^{*}\) является компактной, полностью отделимой группой. Далее мы показываем, что отображение, сопоставляющее элементу \(n\in{\mathbb{Z}}\) элемент \(f_{p}^{n}\in G_{p}\), расширяется до биекции между \(\hat{\mathbb{Z}}\) и замкнутой подгруппой \(G_{p}\), порожденной \(f_{p}\). Фактически, изоморфизм следует из изоморфизма между \(G_{p}\) и \(\text{Gal}(\bar{\mathbb{F}}_{p}:{\mathbb{F}}_{p})\), где \(f_{p}\) - это Фробениус. Результат следует из применения _напр._[5] (Глава V, Приложение II, Упражнение 5). Это дает естественное включение \(\hat{\mathbb{Z}}\subset G_{p}\), \(a\mapsto f_{p}^{a}\), в качестве замкнутой подгруппы. Теперь рассмотрим действие произведения группы \(\hat{\mathbb{Z}}\times{\mathbb{R}}_{+}^{*}\) на \(X\times(0,1)\), заданное \[(a,\lambda).(x,\rho)=(f_{p}^{a}\,x,\rho^{\lambda}).\] (203) \[(a,\lambda).(x,\rho)=(f_{p}^{a}\,x,\rho^{\lambda}).\] (203) По конструкции элемент \((1, p)\) в \(\hat{\mathbb{Z}} \times{\mathbb{R}}_{+}^{*}\) действует как \(\sigma\) (_см._ (201)). Фактор-группа \[(\hat{\mathbb{Z}}\times{\mathbb{R}}_{+}^{*})/s^{\mathbb{Z}}\,,\ \ s=(1,p)\] (204) \[(\hat{\mathbb{Z}}\times{\mathbb{R}}_{+}^{*})/s^{\mathbb{Z}}\,,\ \ s=(1,p)\] (204) изоморфен соленоиду \(S\), используя изоморфизм группы \({\mathbb{R}}_{+}^{*}\) с \({\mathbb{R}}\) заданный логарифмом в базе \(p\). Чтобы увидеть, что \(Y\) является главным связным расслоением над \(S\), используется отображение \(\psi\) из уравнения (202) для проверки того, что \(S\) действует свободно на \(Y\). Отношение \(Y\) к действию \(S\) является отношением \(X\) к действию \(\hat{\mathbb{Z}}\). \((2)\) Волокно \(P_{p}({\mathbb{H}}_{\mathbb{Q}})\) имеет каноническую базовую точку, заданную идемпотентом \(u\in P_{p}({\mathbb{H}}_{\mathbb{Q}}),u^{2}=u\). Следовательно, применяя Предложение 9.1, это волокно канонически изоморфно квоциенту \(C_{\mathbb{Q}}/W_{p}\). Идентифицируя \(C_{\mathbb{Q}}\) с \(\hat{\mathbb{Z}}^{*}\times{\mathbb{R}}_{+}^{*}\), этот квоциент совпадает с квоциентом \(G_{p}\times{\mathbb{R}}_{+}^{*}\) по степеням элемента \((p,p)\in G_{p}\times{\mathbb{R}}_{+}^{*}\). При использовании биекции \(\rho\to-\log(\rho)\) из \((0,1)\) в \({\mathbb{R}}_{+}^{*}\), получается та же самая операция, что и в (201), и, следовательно, желаемый изоморфизм. ∎ Чтобы получить аналог, для глобального поля \({\mathbb{K}}={\mathbb{Q}}\), волокна алгебраической кривой \(X^{\rm ab}\), мы должны применить построение Предложения 9.3 к компактному пространству \(X_{p}\), чтобы удовлетворялись следующие требования \((1)\) \(G_{p}\) действует свободно и транзитивно на \(X_{p}\) \((2)\) Частное от \(X_{p}\) по \(f_{p}^{\hat{\mathbb{Z}}}\) канонически изоморфно \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Предложение 8.14 предоставляет естественного кандидата для \(X_{p}\). Кроме того, уравнение (187) показывает, что \(X_{p}\) можно также описать как пространство \({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\), и что каноническая идентификация \(X_{p}/f_{p}^{\hat{\mathbb{Z}}}\) с \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) задается ограничением отображения на неподвижные точки \({\rm Fr}\) как в (188). Мы получаем определение следующей модели для волокна \(Y_{p}\) над конечным простым числом \(p\) \[Y_{p}=\left({\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\times(0,1) \right)/\sigma^{\mathbb{Z}}.\] (205) ### Волокно над архимедовым местом \({\mathbb{Q}}\) Мы переходим к обсуждению аналогов пространств \({\rm Val}_{p}({{\mathbb{Q}}^{\rm\ цик}})\), \(X_{p}\) и \(Y_{p}\), когда \(p\) является архимедовым простым числом \(p=\infty\) (_т.е._ архимедовой оценкой). Пространство \({\rm Val}_{\infty}({{\mathbb{Q}}^{\rm\ цик}})\) является пространством мультипликативных норм на \({{\mathbb{Q}}^{\rm\ цик}}\), ограничение которых на \({\mathbb{Q}}\) является обычным абсолютным значением. Для \(v\in{\rm Val}_{\infty}({{\mathbb{Q}}^{\rm\ цик}})\), полное поле \(({{\mathbb{Q}}^{\rm\ цик}})_{v}\) изоморфно \({\mathbb{C}}\), таким образом можно вывести \[ {\rm Val}_{\infty}({{\mathbb{Q}}^{\rm cyc}})={\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc }},{\mathbb{C}})/\{\pm 1\}\] (206) \] \[ {\rm Val}_{\infty}({{\mathbb{Q}}^{\rm цик}})={\mbox{Hom}}({{\mathbb{Q}}^{\rm цик}},{\mathbb{C}})/\{\pm 1\}\] (206) \] где \(\{\pm 1\}\subset\hat{\mathbb{Z}}^{*}={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{ \mathbb{Q}})\) соответствует комплексной сопряженности. Отсюда следует, что для \(p=\infty\) пространство \(X_{p}\) является просто \[X_{\infty}={\mbox{Hom}}({{\mathbb{Q}}^{\rm цикл.}},{\mathbb{C}}).\] (207) С другой стороны, волокно \(P_{\infty}({\mathbb{H}}_{\mathbb{Q}})\) является фактор-группой \(C_{\mathbb{Q}}/W_{\infty}\), где \(W_{\infty}={\mathbb{R}}^{*}\) - кокомпактная подгруппа \(C_{\mathbb{Q}}\), состоящая из классов идеалей, у которых компоненты равны \(1\) за исключением архимедового места. Затем, мы получаем следующее \[\displaystyle P_{\infty}({\mathbb{H}}_{\mathbb{Q}})=\hat{\mathbb{Z}}^{*}/\{\pm 1\}.\] (208) Это обсуждение показывает, что при \(p=\infty\) нет необходимости в торе маппинга, и ожидаемое волокно просто задается уравнением \[Y_{\infty}={\rm Val}_{\infty}({{\mathbb{Q}}^{\rm cyc}})={\mbox{Hom}}({{\mathbb {Q}}^{\rm cyc}},{\mathbb{C}})/\{\pm 1\}=X_{\infty}/\{\pm 1\}.\] (209) \[Y_{\infty}={\rm Val}_{\infty}({{\mathbb{Q}}^{\rm цикл}})={\mbox{Hom}}({{\mathbb {Q}}^{\rm цикл}},{\mathbb{C}})/\{\pm 1\}=X_{\infty}/\{\pm 1\}.\] (209) ### Окружающее некоммутативное пространство Модель (205) для волокна над рациональным простым числом \(p\) является лишь предварительным шагом к глобальному построению "кривой", которую мы ожидаем заменить, когда \({\mathbb{K}}={\mathbb{Q}}\), геометрическим покрытием \(X^{\rm ab}\). Фактически, все еще необходимо сочетать эти модели в некоммутативное пространство, чтобы учесть наличие поперечных факторов в явных формулах. Мы объясним это более подробно ниже. В [11] мы показали, как определить функцию подсчета \(N(q)\) (распределение на \([1,\infty)\)), которая заменяет классическую функцию подсчета Вейля для поля \({\mathbb{K}}={\mathbb{Q}}\) функций алгебраической кривой \(Y\) над \({\mathbb{F}}_{p}\) (_см._[27, 35]). Функция подсчета Вейля определяет количество рациональных точек на кривой \(Y\), определенных над расширениями поля \({\mathbb{F}}_{q}\) над \({\mathbb{F}}_{p}\) \[\#Y({\mathbb{F}}_{q})=N(q)=q-\sum_{\alpha}\alpha^{r}+1,\qquad q=p^{r}.\] \[\#Y({\mathbb{F}}_{q})=N(q)=q-\sum_{\alpha}\alpha^{r}+1,\qquad q=p^{r}.\] Числа \(\alpha\) являются комплексными корнями характеристического полинома эндоморфизма Фробениуса, действующего на эталовую когомологию \(H^1(Y\otimes \bar{\mathbb{F}}_p, {\mathbb{Q}}_\ell)\) при \(\ell \neq p\). В [11] мы показали, что распределение \(N(q)\), связанное с (полной) функцией Римана зета, описывается аналогичной формулой. \[N(u)=u-\frac{d}{du}\left(\sum_{\rho\in Z}{\rm order}(\rho)\frac{u^{\rho+1}}{ \rho+1}\right)+1.\] (210) где \(Z\) является множеством ненулевых нулей функции Римана зета. Это распределение положительно на интервале \((1,\infty)\) и удовлетворяет всем ожидаемым свойствам функции подсчета. В частности, оно принимает правильное значение \(N(1)=-\infty\), согласуясь с (ожидаемым) значением характеристики Эйлера. В [14] мы углубили эти идеи и объяснили, как реализовать формулу следа, понимая явные формулы в теории чисел, чтобы выразить распределение \(N(q)\) в виде _числа пересечений_, включающих масштабирующее действие группы классов идель на пространство классов адель. Это развитие включает формулу Лефшеца, геометрическая сторона которой соответствует следующему выражению распределения подсчета \(N(u)\). \[N(u) = \frac{d}{du}\varphi(u) + \kappa(u),\ \ \varphi(u) = \sum_{n<u}n\,\Lambda(n).\] (211) Здесь \(\Lambda(n)\) является функцией фон Мангольдта, принимающей значение \(\log p\) для степеней простых чисел \(p^{\ell}\) и нуль в остальных случаях, а \(\kappa(u)\) это распределение, определенное для любой тестовой функции \(f\) как где \(\gamma=-\Gamma^{\prime}(1)\) является постоянной Эйлера. Распределение \(\kappa(u)\) положительно на интервале \((1,\infty)\) и в этой области равно функции \(\kappa(u)=\frac{u^{2}}{u^{2}-1}\). Вклад в считающее распределение \(N(u)\), исходящий из терма \(\frac{d}{du}\varphi(u)\) в (211), можно понять геометрически как происходящий из считающего процесса, выполняемого на волокнах \(Y_{p}\) (каждое из них учитывает дельта-функции, расположенные на степенях \(p\)). Значение \(\log(p)\), получаемое из функции фон-Мангольдта \(\Lambda(n)\), соответствует длине орбиты в картинной торе (_cf._[14], §2.2). С другой стороны, как объяснено в [14], вклад архимедового места нельзя понять наивным образом как простой счетчик точек и его выражение включает поперечностный множитель, измеряющий поперечность действия группы идеальных классов относительно периодических орбит. Это показывает, что периодические орбиты нельзя рассматривать в изоляции и их необходимо рассматривать как (подходяще) вложенные в окружающее пространство аделиевых классов. Это развитие предоставляет ценную подсказку к окончательному построению "кривой" и показывает, что роль эргодической теории и некоммутативной геометрии важна. ### Система BC над \({\mathbb{Z}}\) и \({\mathbb{F}}_{1^{\infty}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}\) Затем мы объясним, как БК-система над \({\mathbb{Z}}\) даёт, для каждого \(p\), естественное вложение волокна \(Y_{p}\) (_см._ (209)) в некоммутативное пространство, построенное с использованием множества \({\mathcal{E}}({\mathbb{C}}_{p})\) \(\mathbb{C}_{p}\)-рациональных точек аффинной групповой схемы \({\mathcal{E}}\), которая описывает абелеву часть системы (_см._ [15]). Поскольку поля \(\mathbb{C}_{p}\) абстрактно попарно изоморфным, полученные пространства также абстрактно изоморфны, но не каноническим образом. В [15], следуя предложению C. Soulé для значения кольца \({\mathbb{F}}_{1^{n}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}\), мы отмечаем, что индуктивный предел \[{\mathbb{F}}_{1^{\infty}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}:=\varinjlim_{n }{\mathbb{F}}_{1^{n}}\otimes_{{\mathbb{F}}_{1}}{\mathbb{Z}}={\mathbb{Z}}[\left(\mathbb{Q}/\mathbb{Z}\right)]\] (213) совпадает с абелевой частью алгебры, определяющей интегральную BC-систему. Описание, данное в той работе, BC-системы как аффинной прогрупповой схемы \({\mathcal{E}}\) над \({\mathbb{Z}}\), вместе с динамикой действия полумоноида эндоморфизмов, позволяет рассматривать ее рациональные точки над любым кольцом \(A\). \[\mathcal{E}(A)=\text{Hom}(\mathbb{Z}[\mathbb{Q}/\mathbb{Z}],A).\] (214) Затем можно реализовать, для каждого рационального простого числа \(p\), каноническое включение \[X_{p}={\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\subset{\mbox{Hom }}({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],{\mathbb{C}}_{p})={\mathcal{E}}({ \mathbb{C}}_{p})\,.\] (215) \[X_{p}={\mbox{Hom}}({\mathbb{Q}}^{\rm cyc,p},{\mathbb{C}}_{p})\subset{\mbox{Hom }}({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],{\mathbb{C}}_{p})={\mathcal{E}}({ \mathbb{C}}_{p})\,.\] (215) Следующий результат показывает, что пространство \[X({\mathbb{C}}_{p}):=\left({\mathcal{E}}({\mathbb{C}}_{p})\times(0,\infty) \right)/({\mathbb{N}}\times\{\pm 1\})\] (216) \[X({\mathbb{C}}_{p}) := \left({\mathcal{E}}({\mathbb{C}}_{p}) \times (0, \infty)\right) / ({\mathbb{N}} \times \{\pm 1\})\] (216) соответствует, для любого \(p\), включая \(p=\infty\), определению аделевого классового пространства \({\mathbb{H}}_{\mathbb{Q}}\). Действие \(m=\pm n\) (в полуполугруппе \({\mathbb{N}}\times\{\pm 1\}\)) является произведением линеаризации действия \(e(\gamma)\mapsto e(m\gamma)\) на (\({\mathbb{C}}_{p}\)-рациональных точках) схемы \({\mathcal{E}}\), с действием на \((0,\infty)\), заданным отображением \(x\mapsto x^{m}\). **Утверждение 9.4**: \((1)\) _Пространство \(X({\mathbb{C}})\) канонически изоморфно пространству классов адель \({\mathbb{H}}_{\mathbb{Q}}\)._ \((2)\) _Подпространство пространства аделов, состоящее из классов, у которых архимедова компонента обращается в ноль, соответствует фактору_ \[\mathcal{E}(\mathbb{C})/(\mathbb{N}\times\{\pm 1\})=\hat{\mathbb{Z}}/(\mathbb{N}\times\{\pm 1\}).\] (217) Доказательство: \((1)\) Пространство \({\mathcal{E}}({\mathbb{C}})\) является пространством комплексных характеров абелевой группы \({\mathbb{Q}}/{\mathbb{Z}}\) и канонически изоморфно \(\hat{\mathbb{Z}}\). Мы используем отображение \(\rho\mapsto-\log(\rho)\) для отображения интервала \((0,\infty)\) в \({\mathbb{R}}\). Под этим отображением преобразование \(x\mapsto x^{m}\) становится умножением на \(m\). Действие \(e(\gamma)\mapsto e(m\gamma)\) на схеме \({\mathcal{E}}\) соответствует умножению на \(m\) в \(\hat{\mathbb{Z}}\). Так как любой класс адель эквивалентен элементу \(\hat{\mathbb{Z}}\times{\mathbb{R}}\), (216) дает, для \(p=\infty\) \[X({\mathbb{C}})=\left(\hat{\mathbb{Z}}\times{\mathbb{R}}\right)/({\mathbb{N}} \times\{\pm 1\})={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}={\mathbb{H}}_{ \mathbb{Q}}.\] (218) \[X({\mathbb{C}})=\left(\hat{\mathbb{Z}}\times{\mathbb{R}}\right)/({\mathbb{N}} \times\{\pm 1\})={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{*}={\mathbb{H}}_{ \mathbb{Q}}.\] (218) \((2)\) следует из идентификации (218).∎ Обратите внимание, что, используя включение \((0,1) \subset (0, \infty)\), можно получить естественное включение \[Y_{p}=\left({\text{Hom}}({\mathbb{Q}}^{\text{cyc,p}},{\mathbb{C}}_{p})\times(0,1) \right)/\sigma^{\mathbb{Z}}\to\left({\mathcal{E}}({\mathbb{C}}_{p})\times(0, \infty)\right)/({\mathbb{N}}\times\{\pm 1\})=X({\mathbb{C}}_{p}).\] Для \(p=\infty\) имеется естественное включение \[Y_{\infty}={\mbox{Hom}}({{\mathbb{Q}}^{\rm cyc}},{\mathbb{C}})/\{\pm 1\}\to \left({\mathcal{E}}({\mathbb{C}})\times(0,\infty)\right)/({\mathbb{N}}\times\{ \pm 1\})=X({\mathbb{C}})\] (219) \[Y_{\infty}={\mbox{Гом}}({{\mathbb{Q}}^{\rm цик}},{\mathbb{C}})/\{\pm 1\}\to \left({\mathcal{E}}({\mathbb{C}})\times(0,\infty)\right)/({\mathbb{N}}\times\{ \pm 1\})=X({\mathbb{C}})\] (219) который получается с использованием канонического включения (215) для \(p=\infty\) и неподвижной точки \(1\in(0,\infty)\). Групповое кольцо \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) является алгеброй Хопфа для копроизведения. \[\Delta(e(\gamma))=e(\gamma)\otimes e(\gamma)\,,\quad~{}\forall\gamma\in{ \mathbb{Q}}/{\mathbb{Z}}\] (220) \[\Delta(e(\gamma))=e(\gamma)\otimes e(\gamma)\,,\quad~{}\forall\gamma\in{ \mathbb{Q}}/{\mathbb{Z}}\] (220) и антипод \(e(\gamma)\mapsto e(-\gamma)\), следовательно \({\mathcal{E}}\) является групповой схемой. **Утверждение 9.5**. Пусть \(A\) - коммутативное кольцо. \((1)\) _Абелева группа \({\mathcal{E}}(A)\) является свободной от кручения._ \((2)\) _Пространство_ \[X(A)=\left({\mathcal{E}}(A)\times(0,\infty)\right)/({\mathbb{N}}\times\{\pm 1\})\] (221) translates to: \[X(A)=\left({\mathcal{E}}(A)\times(0,\infty)\right)/({\mathbb{N}}\times\{\pm 1\})\] (221) Является модулем над гиперкольцом \({\mathbb{H}}_{\mathbb{Q}}\). \((3)\) _Для любого рационального простого числа \(p\), \(X({\mathbb{C}}_{p})\) является свободным модулем ранга один над \({\mathbb{H}}_{\mathbb{Q}}\)._ Доказательство.: \((1)\) У нас есть \[{\mathcal{E}}(A)={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}],A)={ \mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},A^{\times})\] translates to: \[\mathcal{E}(A)=\text{Hom}(\mathbb{Z}[\mathbb{Q}/\mathbb{Z}],A)=\text{Hom}(\mathbb{Q}/\mathbb{Z},A^{\times})\] где вторая Хом-группа взята в категории абелевых групп. Поскольку группа \({\mathbb{Q}}/{\mathbb{Z}}\) является делимой, группа \({\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},H)\) не имеет кручения, для любой абелевой группы \(H\). \((2)\) Сначала покажем, что \(X(A)\) является гипергруппой и на самом деле векторным пространством над гиперполем Краснера \(\mathbf{K}=\{0,1\}\) (_см._[13]). Два абелевых группы \({\mathcal{E}}(A)\) и \((0,\infty)\) обе без кручения, таким образом, получаем \[\left({\mathcal{E}}(A)\times(0,\infty)\right)/({\mathbb{N}}\times\{\pm 1\})= \left(\left({\mathcal{E}}(A)\times(0,\infty)\right)\otimes_{\mathbb{Z}}{ \mathbb{Q}}\right)/{\mathbb{Q}}^{\times}\] (222) которое является проективным пространством, следовательно, векторным пространством над \(\mathbf{K}\) (_см._[13]). Далее мы показываем, что \(X(A)\) является модулем над \({\mathbb{H}}_{\mathbb{Q}}\). Мы используем канонический изоморфизм колец \(\hat{\mathbb{Z}}={\mbox{End}}_{\mathbb{Z}}({\mathbb{Q}}/{\mathbb{Z}})\) для определения следующего гомоморфизма колец из \(\hat{\mathbb{Z}}\) в кольцо \({\mbox{End}}_{\mathbb{Z}}({\mathcal{E}}(A))\) \[c_{A}:\hat{\mathbb{Z}}\to{\mbox{End}}_{\mathbb{Z}}({\mathcal{E}}(A))\,,\ \ c_{ A}(\alpha)\xi=\xi\circ\alpha\,,\quad~{}\forall\xi\in{\mbox{Hom}}({\mathbb{Q}}/ {\mathbb{Z}},A^{\times}).\] (223) \[c_A: \hat{\mathbb{Z}} \rightarrow {\mbox{End}}_{\mathbb{Z}}({\mathcal{E}}(A))\,, \ \ c_{A}(\alpha)\xi=\xi\circ\alpha\,, \quad~{} \forall\xi\in{\mbox{Hom}}({\mathbb{Q}}/ {\mathbb{Z}},A^{\times}).\] (223) ``` Карта ``` If you have any equations that you would like me to preserve the form of, please include them and I will do my best to assist you. \[p:{\mathbb{R}}\to{\mbox{End}}_{\mathbb{Z}}({\mathbb{R}}_{+}^{*}),\quad p( \lambda)x=x^{\lambda}\] (224) \[p: {\mathbb{R}} \rightarrow {\mbox{End}}_{\mathbb{Z}}({\mathbb{R}}_{+}^{*}),\quad p( \lambda)x=x^{\lambda}\] (224) является гомоморфизмом колец, таким образом \(c_{A}\times p\) определяет гомоморфизм колец из \(\hat{\mathbb{Z}}\times{\mathbb{R}}\) в эндоморфизмы абелевой группы \({\mathcal{E}}(A)\times(0,\infty)\). Для любого \(m\in{\mathbb{Z}}\subset\hat{\mathbb{Z}}\times{\mathbb{R}}\), имеем \[(c_{A}\times p)(m)((e(\gamma),x))=(e(m\gamma),x^{m}),\] (225) \[(c_{A}\times p)(м)((е(\gamma),x))=(е(m\gamma),x^{m}),\] (225) таким образом, ограничение \(c_{A} \times p\) на моноид ненулевых элементов \({\mathbb{Z}}\) дает эквивалентное отношение, которое определяет \(X(A)\) как в (221). Следовательно, имеется действие полукольца \[\left((\hat{\mathbb{Z}}\times{\mathbb{R}})\otimes_{\mathbb{Z}}{\mathbb{Q}} \right)/{\mathbb{Q}}^{\times}={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{\times}= {\mathbb{H}}_{\mathbb{Q}}\] translates to: \[\left((\hat{\mathbb{Z}}\times{\mathbb{R}})\otimes_{\mathbb{Z}}{\mathbb{Q}} \right)/{\mathbb{Q}}^{\times}={\mathbb{A}}_{\mathbb{Q}}/{\mathbb{Q}}^{\times}= {\mathbb{H}}_{\mathbb{Q}}\] в гипергруппе (222). \((3)\) Легко видеть, что после фиксации вложения \(\rho:{{\mathbb{Q}}^{\rm cyc}}\to{\mathbb{C}}_{p}\) и числа \(x\in(0,\infty)\) и \(x\neq 1\), элемент \((\rho,x)\in X({\mathbb{C}}_{p})\) является порождающим множеством \(X({\mathbb{C}}_{p})\) как свободного модуля над \({\mathbb{H}}_{\mathbb{Q}}\). ∎ Следующий результат показывает некоторые интересные арифметико-геометрические свойства схемы \({\mathcal{E}}\). **Утверждение 9.6**. \((1)\) _Пусть \({\mathbb{Q}}_{p}^{\rm ab}\subset{\mathbb{C}}_{p}\) является максимальным абелевым расширением \({\mathbb{Q}}_{p}\). Тогда естественное отображение \({\mathcal{E}}({\mathbb{Q}}_{p}^{\rm ab})\to{\mathcal{E}}({\mathbb{C}}_{p})\) является взаимно однозначным отображением множеств._ (2) _Пусть \({\mathbb{Q}}_{p}^{\rm ur}\subset{\mathbb{Q}}_{p}^{\rm ab}\) будет максимальным некрамеровским расширением \({\mathbb{Q}}_{p}\), а \({\mathbb{Z}}_{p}^{\rm ur}\subset{\mathbb{Q}}_{p}^{\rm ur}\) - это кольцо оценки \(p\)-адической оценки. Тогда естественное отображение \({\mathcal{E}}({\mathbb{Z}}_{p}^{\rm ur})\to{\mathcal{E}}({\mathbb{Q}}_{p}^{\rm ur})\) является биекцией множеств._ \((3)\) _Пусть \(\epsilon:{\mathbb{Z}}_{p}^{\rm ur}\to\bar{\mathbb{F}}_{p}\) будет отображением остатков. Тогда соответствующее отображение \({\mathcal{E}}({\mathbb{Z}}_{p}^{\rm ur})\to{\mathcal{E}}(\bar{\mathbb{F}}_{p})\) является биекцией._ \((4)\) _Модуль \({\mathbb{H}}_{\mathbb{Q}}\)_ \ [X(\bar{\mathbb{F}}_{p})\simeq X({\mathbb{Z}}_{p}^{\rm ur})\simeq X({\mathbb{Q} }_{p}^{\rm ur})\subset X({\mathbb{Q}}_{p}^{\rm ab})\simeq X({\mathbb{C}}_{p})\] should be translated to Russian as: \[X(\bar{\mathbb{F}}_{p})\simeq X({\mathbb{Z}}_{p}^{\rm ur})\simeq X({\mathbb{Q} }_{p}^{\rm ur})\subset X({\mathbb{Q}}_{p}^{\rm ab})\simeq X({\mathbb{C}}_{p})\] _описывается как_ \[X(\bar{\mathbb{F}}_{p})=\mathfrak{p}_{p}X({\mathbb{C}}_{p})\] (226) \[X(\bar{\mathbb{F}}_{p})=\mathfrak{p}_{p}X({\mathbb{C}}_{p})\] (226) _где \(\mathfrak{p}_{p}\in{\rm Spec}\,({\mathbb{H}}_{\mathbb{Q}})\) - это простой идеал классов адель, компонента \(p\)-компонента которого обращается в ноль._ Доказательство. (1) Пусть \(\rho\in{\mathcal{E}}({\mathbb{C}}_{p})={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/ {\mathbb{Z}}],{\mathbb{C}}_{p})\). Тогда образ \(\rho\) содержится в подполе \({\mathbb{C}}_{p}\), порожденном над \({\mathbb{Q}}\) корнями из единицы, которое содержится в \({\mathbb{Q}}_{p}^{\rm ab}\). \((2)\) Пусть \(\rho\in{\mathcal{E}}({\mathbb{Q}}_{p}^{\rm ur})={\mbox{Hom}}({\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],{\mathbb{Q}}_{p}^{\rm ur})\). Тогда образ \(\rho\) содержится в подкольце \({\mathbb{Q}}_{p}^{\rm ur}\), порожденном над \({\mathbb{Z}}\) корнями из единицы (порядок которых взаимно прост с \(p\)), которое содержится в \({\mathbb{Z}}_{p}^{\rm ur}\). \((3)\) Пусть \(\rho\in{\mathcal{E}}({\mathbb{Z}}_{p}^{\rm ur})={\mbox{Hom}}({\mathbb{Z}}[{ \mathbb{Q}}/{\mathbb{Z}}],{\mathbb{Z}}_{p}^{\rm ur})\). Тогда \(\rho\) полностью определяется гомоморфизмом группы. \[\rho:{\mathbb{Q}}/{\mathbb{Z}}\to G\] translates to: \[\rho:{\mathbb{Q}}/{\mathbb{Z}}\to G\] где \(G\) является группой корней из единицы в \({\mathbb{Z}}_{p}^{\rm ur}\), которая не канонически изоморфна группе \(\mu^{(p)}\) абстрактных корней из единицы порядка, взаимно простого с \(p\). Аналогично, элемент из \({\mathcal{E}}(\bar{\mathbb{F}}_{p})={\mbox{Hom}}({\mathbb{Z}}[{\mathbb{Q}}/{ \mathbb{Z}}],\bar{\mathbb{F}}_{p})\) полностью характеризуется связанной гомоморфизмом группы из \({\mathbb{Q}}/{\mathbb{Z}}\) в \(\bar{\mathbb{F}}_{p}^{*}\). Так как морфизм остатков \(\epsilon\) дает изоморфизм \(G\stackrel{{\simeq}}{{\to}}\bar{\mathbb{F}}_{p}^{*}\), получается заключение. (4) Имеется \(\hat{\mathbb{Z}}={\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},{\mathbb{Q}}/{\mathbb{ Z}})\). Пусть, как указано выше, \({({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}\subset{\mathbb{Q}}/{\mathbb{Z}}\) является подгруппой элементов с знаменателем, взаимно простым с \(p\). Тогда подмножество \({\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},{({\mathbb{Q}}/{\mathbb{Z}})^{(p)}}) \subset{\mbox{Hom}}({\mathbb{Q}}/{\mathbb{Z}},{\mathbb{Q}}/{\mathbb{Z}})\) задается \[\{(a_{\ell})\in\prod{\mathbb{Z}}_{\ell}=\hat{\mathbb{Z}}\mid\ \ a_{p}=0\}\] translates to: \[\{(a_{\ell})\in\prod{\mathbb{Z}}_{\ell}=\hat{\mathbb{Z}}\mid\ \ a_{p}=0\}\] которая соответствует простым, главным идеалам \(\mathfrak{p}_{p}\) структуры гиперкольца \({\mathbb{H}}_{\mathbb{Q}}\), связанных с аделическим классом (_см._[13]). ∎ ## 10. Стандартная модель \(\bar{\mathbb{F}}_{p}\) и BC-система Как показано в разделе 8, пространство \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) тесно связано со структурой последовательностей неприводимых многочленов \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), удовлетворяющих основным условиям полиномов Конвея (_см._ Теорема 8.7), а также с явным построением алгебраического замыкания \({\mathbb{F}}_{p}\). Нормализационное условие, использующее лексикографическое упорядочение, просто задает конкретный элемент \(v_{c}\) в пространстве \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Поскольку явное вычисление последовательности \(P_{n}(T)\in{\mathbb{F}}_{p}[T]\), \(n\in{\mathbb{N}}\), связанной с \(v_{c}\), оказалось полностью неосуществимым, B. de Smit и H. Lenstra недавно разработали более эффективное построение \(\bar{\mathbb{F}}_{p}\) (_см._[18]). Цель данного раздела - явно определить связь между их построением, BC-системой и искомой "кривой". Когда \({\mathbb{K}}\) является глобальным полем положительной характеристики, то есть функциональным полем алгебраической кривой над конечным полем \({\mathbb{F}}_{q}\), промежуточное расширение \({\mathbb{K}}\subset\bar{\mathbb{F}}_{q}\otimes_{{\mathbb{F}}_{q}}{\mathbb{K}} \subset{\mathbb{K}}^{\rm ab}\) играет важную геометрическую роль, так как оно соответствует работе над алгебраически замкнутым полем. Для \({\mathbb{K}}={\mathbb{Q}}\) естественно спросить о промежуточном расширении \({\mathbb{Q}}\subset L\subset{{\mathbb{Q}}^{\rm cyc}}\), играющем аналогичную роль. Одной из особенностей первого расширения является то, что полевые остатки являются алгебраически замкнутыми. В своей конструкции де Смит и Ленстра используют промежуточное расширение \({\mathbb{Q}}\subset{{\mathbb{Q}}^{\rm cycl}_{\Delta}}\subset{{\mathbb{Q}}^{\rm cyc}}\), которое очень близко подходит к ожидаемым свойствам. Для каждого простого числа \(\ell\) обозначим \(\Delta_{\ell}\subset{\mathbb{Z}}_{\ell}^{*}\) подгруппу кручения. Для \(\ell=2\) имеем \(\Delta_{2}=\{\pm 1\}\), в то время как для \(\ell\neq 2\) получаем \(\Delta_{\ell}=\tau({\mathbb{F}}_{\ell}^{*})\), где \(\tau:{\mathbb{F}}_{\ell}\to{\mathbb{Z}}_{\ell}\) - это подъем Тайхмюллера. Произведение \[\Delta:=\prod_{\ell}\Delta_{\ell}\subset\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}\] (227) \[\Delta:=\prod_{\ell}\Delta_{\ell}\subset\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}\] (227) это компактная группа и подгруппа галуаевой группы \(\hat{\mathbb{Z}}^{*}={\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\). Согласно теории Галуа, к \(\Delta\) можно также присоединить (фиксированное) расширение поля. \[\mathbb{L}={{\mathbb{Q}}^{\rm cyl}_{\Delta}}\subset{{\mathbb{Q}}^{\rm цик}}.\] (228) Обратите внимание, что подсистема BC-системы получается путем нахождения неподвижных точек действия \(\Delta\). На рациональном уровне, реализуя циклотомический идеал \(J\) из Определения 8.1, мы получаем точную последовательность алгебр \[0\to J\cap{{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\to{{\mathbb{Q}}[{ \mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\stackrel{{ q}}{{\to}}{{\mathbb {Q}}^{\rm cycl}_{\Delta}}\to 0\] (229) \[0\to J\cap{{\mathbb{Q}}[{\mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\to{{\mathbb{Q}}[{ \mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\stackrel{{ q}}{{\to}}{{\mathbb {Q}}^{\rm cycl}_{\Delta}}\to 0\] (229) Изображение ограничения на \({{\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]^{\Delta}}\) гомоморфизма \(q\) содержится в целых числах \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\) и имеется следующее выражение: \[{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\simeq\hat{\mathbb{Z }}^{*}/\Delta\simeq\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}.\] (230) \[{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\simeq\hat{\mathbb{Z }}^{*}/\Delta\simeq\prod_{\ell}{\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}.\] (230) Пространство \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\) является полным пространством главного пучка, основанием которого является пространство \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) измерений на \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\), продолжающих \(p\)-адическую оценку. Группа главного пучка является фактором \(\Delta\) по пересечению \(\Delta_{p}\) с изотропной группой элементов \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\). Отображение \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\to{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) задается ограничением оценок с \({{\mathbb{Q}}^{\rm cyc}}\) на \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\). Для \(w\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\), изотропная группа \(\Pi_{p}\) для действия \({\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\) на \(w\) является образом изотропной группы \(v\) в \({\rm Gal}({{\mathbb{Q}}^{\rm cyc}}:{\mathbb{Q}})\) для любого разбиения \(v\) \(w\) на \({{\mathbb{Q}}^{\rm cyc}}\). Следовательно, из Леммы 8.2 следует, что изотропная подгруппа \(v\) является \({\mathbb{Z}}_{p}^{*}\times f_{p}^{\hat{\mathbb{Z}}}\subset{\mathbb{Z}}_{p}^{*} \times G_{p}\), таким образом, получаем \[\Pi_{p}\simeq{\mathbb{Z}}_{p}^{*}/\Delta_{p}\times\overline{f_{p}^{\mathbb{Z}} }\,,\ \ \overline{f_{p}^{\mathbb{Z}}}\subset\prod_{\ell\neq p}{\mathbb{Z}}_{ \ell}^{*}/\Delta_{\ell}.\] (231) \[\Pi_{p}\approx\frac{\mathbb{Z}_{p}^{*}}{\Delta_{p}}\times\overline{f_{p}^{\mathbb{Z}} }\,,\ \ \overline{f_{p}^{\mathbb{Z}}}\subset\prod_{\ell\neq p}{\mathbb{Z}}_{ \ell}^{*}/\Delta_{\ell}.\] (231) **Лемма 10.1**. _Для каждого простого числа \(\ell\) группа \({\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\) канонически изоморфна аддитивной группе \({\mathbb{Z}}_{\ell}\). Более того, для каждого простого числа \(p\neq\ell\) замкнутая подгруппа в \({\mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\), порожденная \(p\), является открытой и имеет конечный индекс \(\ell^{u(p,\ell)}\), где_ \[u(p,\ell)=\begin{cases}v_{\ell}(p^{\ell-1}-1)-1,&\text{для $\ell>2$}\\ v_{2}(p^{2}-1)-3,&\text{для $\ell=2$.}\end{cases}\] (232) Доказательство.: Для каждого простого числа \(\ell\) существует канонический изоморфизм группы \[\mathbb{Z}_{\ell}^{*}\stackrel{\sim}{\to}\Delta_{\ell}\times \mathbb{Z}_{\ell},\quad x\mapsto(\omega(x),i_{\ell}(x))\] (233) где группа \({\mathbb{Z}}_{\ell}\) рассматривается как аддитивная группа. В случае нечетного \(\ell\), \(\omega(x)\) является единственным корнем из \(\ell-1\) единичного модуля, конгруентного \(x\) по модулю \(\ell\), а \(i_{\ell}(x)\), как в (145), является отношением \({\log_{\ell}x/\log_{\ell}(1+\ell)}\). Для \(\ell=2\), \(\omega(x)=\pm 1\) сравнимо с \(x\) по модулю \(4\), и \(i_{2}(x)=\log_{2}x/\log_{2}(1+4)\). Таким образом, первое утверждение следует. Второе утверждение следует, так как выполняется \[v_{\ell}(i_{\ell}(p))=u(p,\ell)\] translates to Russian as: \[v_{\ell}(i_{\ell}(p))=u(p,\ell)\] и замкнутая подгруппа \({\mathbb{Z}}_{\ell}\), порожденная \(i_{\ell}(p)\), равна \(\ell^{u(p,\ell)}{\mathbb{Z}}_{\ell}\).∎ Под изоморфизмами \[{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\simeq\prod_{\ell}{ \mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\simeq\prod_{\ell}{\mathbb{Z}}_{\ell} \simeq\hat{\mathbb{Z}}\] (234) \[\text{Гал}({{\mathbb{Q}}^{\text{цикл}}_{\Delta}}:{\mathbb{Q}})\simeq\prod_{\ell}{ \mathbb{Z}}_{\ell}^{*}/\Delta_{\ell}\simeq\prod_{\ell}{\mathbb{Z}}_{\ell} \simeq\hat{\mathbb{Z}}\] (234) получается, по китайской теореме об остатках, что \[\Pi_{p}\simeq{\mathbb{Z}}_{p}\times\prod_{\ell\neq p}\ell^{u(p,\ell)}{\mathbb{ Z}}_{\ell}\subset\hat{\mathbb{Z}}\,.\] (235) \[\Pi_{p}\simeq{\mathbb{Z}}_{p}\times\prod_{\ell\neq p}\ell^{u(p,\ell)}{\mathbb{ Z}}_{\ell}\subset\hat{\mathbb{Z}}\,.\] (235) Обратите внимание на независимость мест \(\ell\) в приведенной формуле, что делает группу \(\Pi_{p}\) декартовым произведением и позволяет выразить \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) в виде бесконечного произведения конечных множеств. Для явной классификации этих конечных множеств рассмотрим для каждого простого числа \(\ell\) расширение \({\mathbb{Z}}_{\ell}\)-полей \({\mathbb{B}}_{\infty}(\ell)\) над \({\mathbb{Q}}\). Имеем \({\mathbb{B}}_{\infty}(\ell)=\cup_{k}{\mathbb{B}}_{k}(\ell))\), где для \(k\in{\mathbb{N}}\) конечное расширение \({\mathbb{B}}_{k}(\ell)\) поля \({\mathbb{Q}}\) связано с элементом \(\ell^{-k}\in{\mathbb{Q}}/{\mathbb{Z}}\), рассматриваемым как характер \(\hat{\mathbb{Z}}\simeq{\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\). Для нечётного \(\ell\) поле \({\mathbb{B}}_{k}(\ell)\) является полем инвариантов действия \(\Delta_{\ell}\) на расширении \({\mathbb{Q}}\), порождённом первообразным корнем из единицы порядка \(\ell^{k+1}\). Для \(\ell=2\) используется первообразный корень из единицы порядка \(2^{k+2}\). Обозначим \({\mathbb{B}}(\ell,p)={\mathbb{B}}_{u(p,\ell)}(\ell)\): это циклическое расширение поля \({\mathbb{Q}}\) степени \(\ell^{u(p,\ell)}\). Закон взаимности Артена показывает, что для простого числа \(p\neq\ell\) остаток по модулю \(p\) элементов поля \({\mathbb{B}}(\ell,p)\) разлагается в произведение \(\ell^{u(p,\ell)}\) копий поля \({\mathbb{F}}_{p}\), параметризованных множеством \({\rm Val}_{p}({\mathbb{B}}(\ell,p))\) расширений \(p\)-адической нормы на поле \({\mathbb{B}}(\ell,p)\), которое является конечным множеством мощности \(\ell^{u(p,\ell)}\). Следующий результат является следствием построения "стандартной модели" де Смита и Ленстры для алгебраического замыкания конечного поля. **Теорема 10.2****.**: _Пусть \(p\) - рациональное простое число._ \((1)\) _Для простых чисел \(\ell\neq p\), отображение ограничения \({\rm Val}_{p}({\mathbb{B}}_{\infty}(\ell))\to{\rm Val}_{p}({\mathbb{B}}(\ell,p))\) является биекцией._ \((2)\) _Ограничительные отображения из \({{\mathbb{Q}}^{\rm cycl}_{\Delta}}\) в \({\mathbb{B}}_{\infty}(\ell)\) дают взаимно однозначное соответствие_. \[\text{{Val}}_{p}({{\mathbb{Q}}^{\text{{cycl}}}_{\Delta}})=\prod_{\ell\neq p}{\text{{Val}}}_ {p}({\mathbb{B}}_{\infty}(\ell)).\] (236) \((3)\) _Ограничение \(v\in{\rm Val}_{p}({{\mathbb{Q}}^{\rm cycl}_{\Delta}})\) на \({\mathbb{Q}}^{\rm cyc,p}_{\Delta}\) является неразветвленным, а поле остатков изоморфно_ \[ \bigcup_{n\in I(p)}{\mathbb{F}}_{p^{n}} \subset \bar{\mathbb{F}}_{p} \] (237) _где \(I(p)\subset{\mathbb{N}}\) обозначает подмножество положительных целых чисел, взаимно простых с \(p\)._ Доказательство: \((1)\) Достаточно показать, что образ изотропной группы \({\mathbb{Z}}_{p}^{*}\times p^{\hat{\mathbb{Z}}}\subset{\mathbb{Z}}_{p}^{*} \times G_{p}\) по Лемме 8.2 отображается сюръективно на группу Галуа \({\rm Gal}({\mathbb{B}}_{\infty}(\ell):{\mathbb{B}}(\ell,p))\). Это следует из Леммы 10.1. \((2)\) Ограничительные отображения определяют эквивариантное отображение \[\mathrm{Val}_{p}(\mathbb{Q}^{\mathrm{cycl}_{\Delta}})\rightarrow\prod_{\ell\neq p}\mathrm{Val}_{p}(\mathbb{B}_{\infty}(\ell))\] (238) для действия группы Галуа \({\rm Gal}({{\mathbb{Q}}^{\rm cycl}_{\Delta}}:{\mathbb{Q}})\). По (234) и (235), группы изотропии одинаковы, так что отображение (238) является биективным. \((3)\) Расширяя \(v\) до элемента \({\rm Val}_{p}({{\mathbb{Q}}^{\rm cyc}})\), мы получаем, что ограничение на \({\mathbb{Q}}^{\rm cyc,p}\) и, следовательно, на \({\mathbb{Q}}^{\rm cyc,p}_{\Delta}\) является неразветвленным. Более того, поле остатков определяется топологией на замыкании действия Фробениуса, _т.е._ на \(\prod_{\ell\neq p}{\mathbb{Z}}_{\ell}\). Результат следует.∎ Далее мы объясним связь с обозначениями, используемыми де Смитом и Ленстрой, а также их построение. Во-первых, напомним, что аддитивная группа \({\mathbb{Q}}/{\mathbb{Z}}\) является прямой суммой её \(\ell\)-торсионных компонент \[\(H_{\ell}=\{\alpha\in{\mathbb{Q}}/{\mathbb{Z}}\mid\exists n\ \ell^{n}\alpha=0\} \simeq{\mathbb{Q}}_{\ell}/{\mathbb{Z}}_{\ell}\). (239)\] Таким образом, групповое кольцо \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) можно записать в виде тензорного произведения \[\mathbb{Z}[\mathbb{Q}/\mathbb{Z}] = \bigotimes_{\ell \, \rm prime} \mathbb{Z}[H_{\ell}].\] (240) Естественное действие \(\hat{\mathbb{Z}}^{*}\) на \({\mathbb{Z}}[{\mathbb{Q}}/{\mathbb{Z}}]\) автоморфизмами группы \({\mathbb{Q}}/{\mathbb{Z}}\) факторизуется в отдельные действия \({\mathbb{Z}}_{\ell}^{*}={\rm Aut}(H_{\ell})\). Предположим \(A_{\ell}\) - это кольцо \({\mathbb{Z}}[X_{0},X_{1},\ldots]\) по модулю идеала, порожденного \[\sum_{j=0}^{\ell-1}X_{0}^{j}\,,\ \ X_{k+1}^{\ell}-X_{k}\,,\quad~{}\forall k \geq 0.\] (241) \[\sum_{j=0}^{\ell-1}X_{0}^{j}\,,\ \ X_{k+1}^{\ell}-X_{k}\,,\quad~{}\forall k \geq 0.\] (241) Таким образом, для всех \(k\geq 0\) выполняется \(X_{0}^{\ell}=1\) в \(A_{\ell}\), а \(X_{k+1}^{\ell}=X_{k}\). Алгебра \(B_{\ell}\) Де Смита и Ленстры определяется как \(B_{\ell}=A_{\ell}^{\Delta_{\ell}}\). Следующая лемма показывает, что алгебра \(B_{\ell}\) тесно связана с алгеброй фиксированной точки \({\mathbb{Z}}[H_{\ell}]^{\Delta_{\ell}}\). **Лемма 10.3****.**: _Имеется_ \[B_{\ell}\simeq({\mathbb{Z}}[H_{\ell}]/J)^{\Delta_{\ell}}\] (242) _где \(J\) является идеалом, порожденным отношениями \(\sum_{\ell\gamma=0}e(\gamma)\in{\mathbb{Z}}[H_{\ell}]\)._ Доказательство. Из соотношений (241) следует, что \(X_{k}^{\ell^{k+1}}=1\) для всех \(k\). Кроме того, отображение \(\theta(e(\ell^{-k}))=X_{k-1}\) расширяется до сюръективного гомоморфизма \({\mathbb{Z}}[H_{\ell}]\to A_{\ell}\) с ядром \(J\), отсюда получается (242).∎ Переведено на русский язык с сохранением формулы: У нас есть отображение следа \[\Sigma: A_{\ell} \to B_{\ell}, \qquad \Sigma(x) = \sum_{\sigma \in \Delta_{\ell}} \sigma(x)\] (243) и естественное кольцевое гомоморфизмы \(B_{\ell}\to E(\ell)\). Де Смит и Ленстра (_см._ [18]) поднимают естественный генератор \(E_{k}(\ell)\) как расширение \(E_{k-1}(\ell)\), а галуа-сопряженные элементы под действием \({\rm Gal}(E_{k}(\ell):E_{k-1}(\ell))\) как следующие элементы \(B_{\ell}\). \[\eta_{\ell,k,i}=\Sigma(e(\frac{1}{\ell^{k+1}}+\frac{i}{\ell})),\ \ i=0,\ldots \ell-1.\] (244) translates to: \[\eta_{\ell,k,i}=\Sigma(e(\frac{1}{\ell^{k+1}}+\frac{i}{\ell})),\ \ i=0,\ldots \ell-1.\] (244) Когда \(\ell=2\), у нас просто \({\Delta_{2}}=\{\pm 1\}\subset{\mathbb{Z}}_{2}^{*}\), и в этом случае вышеупомянутый список элементов сокращается до \[\eta_{2,k}=\Sigma(e(\frac{1}{2^{k+2}})).\] (245) \[\eta_{2,k}=\Sigma(e(\frac{1}{2^{k+2}})).\] (245) Два автора показывают, что простые идеалы \(\mathfrak{p}\) в \(B_{\ell}\), содержащие \(p\), однозначно определяются конечной системой элементов \(a(\mathfrak{p},j) \in \mathbb{F}_p\), \(0 \leq j < \ell u(p,\ell)\). Более точно, \(\mathfrak{p}\) порождается \(p\) и элементами \(\eta_{\ell,k+1,i} - a(\mathfrak{p},i+k\ell)\) для \(0 \leq k < u(p,\ell)\) и \(0 \leq i < \ell\). Чтобы завершить словарь с обозначениями де Смита и Ленстры, мы оставляем читателю в качестве упражнения показать, что \(\bullet\) Простые идеалы \(\mathfrak{p}\), содержащие \(p\), в соответствии с оценками \({\rm Val}_{p}({\mathbb{B}}_{\infty}(\ell))\) для \(B_{\ell}\). \(\bullet\) Подполе \({\mathbb{Q}}_{p}\cap{\mathbb{B}}_{\infty}(\ell)\subset{\mathbb{B}}_{\infty}( \ell)_{v}\) равно \({\mathbb{B}}(\ell,p)\). \(\bullet\) Система элементов \(a(\mathfrak{p},j) \in \mathbb{F}_p\) соответствует, как в Предложении 8.13, остатку включения \(\gamma_v: \mathbb{B}(\ell,p) \to \mathbb{Q}_p\), определенного, как в Предложении 8.12. Теорема 10.2 не дает полного алгебраического замыкания \({\mathbb{F}}_{p}\), а только подполе \[\bigcup_{n\in I(p)}{\mathbb{F}}_{p^{n}}\subset\bar{\mathbb{F}}_{p}.\] (246) \[\bigcup_{n\in I(p)}{\mathbb{F}}_{p^{n}}\subset\bar{\mathbb{F}}_{p}.\] (246) Таким образом, остаётся понять, как естественно создать отсутствующую часть. \[ \bigcup_{n} {\mathbb{F}}_{p^{p^{n}}} \subset \bar{\mathbb{F}}_{p} \] (247) \[ \bigcup_{n} \mathbb{F}_{p^{p^{n}}} \subset \bar{\mathbb{F}}_{p} \] (247) таким образом, тензорное произведение над \({\mathbb{F}}_{p}\) дает \(\bar{\mathbb{F}}_{p}\). Конструкция Де Смита и Ленстры \({\mathbb{F}}_{p^{p^{\infty}}}=\varinjlim_{n}{\mathbb{F}}_{p^{p^{n}}}\) выполняется с использованием следующих уравнений Артин-Шрайера. \[y_{0}^{p}-y_{0}=1\,,\ \ y_{n+1}^{p}-y_{n+1}+\frac{y_{n}}{y_{n}+1}=0\,,\quad~{} \forall n\geq 0\] (248) \[y_{0}^{p}-y_{0}=1\,,\ \ y_{n+1}^{p}-y_{n+1}+\frac{y_{n}}{y_{n}+1}=0\,,\quad~{} \forall n\geq 0\] (248) которые имеют преимущество простоты. Э. Витт в [38] предложил концептуальную конструкцию \({\mathbb{F}}_{p^{p^{\infty}}}\) на основе виттовского функтора \({\mathbb{W}}_{p^{\infty}}\) и его конечных обрезоков \({\mathbb{W}}_{p^{n}}\). Сложение двух виттовских векторов \(x=(x_{j})\) и \(y=(y_{j})\) является вектором, компоненты которого \(S_{j}(x,y)\) были доказаны Виттом быть многочленами с целыми коэффициентами. Также обратите внимание, что для \(p\neq 2\) виттовские компоненты \(-x\) (аддитивная инверсия \(x\)) просто равны \(-x_{j}\), но это свойство не выполняется для \(p=2\). Также напомним, что в терминах виттовских векторов Фробениус \(F\) в характеристике \(p\) задается как \((F(x))_{j}=x_{j}^{p}\,,\quad~{}\forall j\). Из [38] следует следующий результат **Теорема 10.4:** _Пусть \(n\in{\mathbb{N}}\). Пусть \(R_{n}={\mathbb{F}}_{p}[x_{0},x_{1},\ldots,x_{n-1}]\) - кольцо полиномов в \(n\) переменных, а \(J_{n}\subset R_{n}\) - идеал, порожденный компонентами вектора Витта \(F(x)-x-1\), где \(x\in{\mathbb{W}}_{p^{n-1}}(R)\) - вектор Витта с компонентами \(x_{j}\). Тогда \(J_{n}\) - простой идеал, а поле частных интегрального кольца \(R_{n}/J_{n}\) определяет расширение полей \(E_{n}\simeq{\mathbb{F}}_{p^{p^{n}}}\)._ _В качестве расширения \(E_{n-1}\), \(E_{n}\) задается уравнением Артина-Шрайера следующего вида_ \[X^{p}=X+\alpha,\ \ \alpha\in E_{n-1}.\] (249) \[X^{p}=X+\alpha,\ \ \alpha\in E_{n-1}.\] (249) Из этого следует, например, что первые расширения для \(p=2\) задаются уравнениями с коэффициентами в \({\mathbb{F}}_{2}\). \[x_{0}^{2} = 1+x_{0}\] \[x_{1}^{2} = x_{0}+x_{1}\] \[x_{2}^{2} = x_{0}+x_{0}^{3}+x_{0}x_{1}+x_{2}\] \[x_{3}^{2} = x_{0}+x_{0}^{3}+x_{0}^{5}+x_{0}^{7}+x_{0}^{2}x_{1}+x_{0}^{3}x_{1 }+x_{0}^{4}x_{1}+x_{0}x_{1}^{3}+x_{0}x_{2}+x_{0}^{3}x_{2}+x_{0}x_{1}x_{2}+x_{3}\] Для \(p=3\) получим следующие уравнения с коэффициентами в \({\mathbb{F}}_{3}\) \[\displaystyle x_{0}^{3}=1+x_{0}\] \[\displaystyle x_{1}^{3}=2x_{0}+2x_{0}^{2}+x_{1}\] \[\displaystyle x_{2}^{3}=2x_{0}+2x_{0}^{2}+2x_{0}^{4}+2x_{0}^{5}+2x_{0}^{7}+2x_{0}^{8}+2x _{0}^{2}x_{1}+x_{0}^{3}x_{1}+2x_{0}^{4}x_{1}+x_{0}x_{1}^{2}+x_{0}^{2}x_{1}^{2}+x_{2}\] Таким образом, можно получить полностью каноническое построение поля \({\mathbb{F}}_{p^{p^{\infty}}}\), просто записав уравнение \(F(X)=X+1\) в кольце Виттовых векторов \({\mathbb{W}}_{p^{\infty}}\). ## Ссылки * [1] Г. Альмквист, _Эндоморфизмы конечномерных проективных модулей над коммутативным кольцом_, Arkiv för Matematik Том 11, Номера 1-2 (1973), 263–301. * [2] Г. Альмквист, _Кольцо Гротендика категории эндоморфизмов_, J. of Algebra 28,(1974), 375–388. * [3] Р. Ауэр, _Функториальное свойство вложенных векторов Витта_, J. of Algebra 252 (2002), 293–299. * [4] Д. Бост, А. Коннес, _Алгебры Хекке, тип III факторы и фазовые переходы со спонтанным нарушением симметрии в теории чисел_, Selecta Math. (N.S.) 1 (1995), no. 3, 411–457. * [5] Н. Бурбаки _Алгебра II. Главы 4–7_. Перевод с французского варианта 1981 года П. М. Кона и Дж. Хауи. Переиздание английского варианта 1990 года. Элементы математики (Берлин). Springer-Verlag, Берлин, 2003. * [6] П. Картье, _Формальные группы, связанные с обобщенными векторами Витта_, Compt. Rend. Acad. Sci. Paris, Ser. A-B 265 (1967), A49–A52. * [7] А. Коннес, _Формула следа в некоммутативной геометрии и нули функции Римана_, Selecta Math. (N.S.) 5 (1999), no. 1, 29–106. * [8] А. Коннес _Виттовская конструкция в характеристике один и квантование_, появится в сборнике трудов, посвященном Х. Московичи (2011). * [9] А. Коннес _Система BC и L-функции_, появится в японском журнале математики. * [10] А. Коннес, К. Консани _О представлении геометрии над \({\mathbb{F}}_{1}\)_, появится в Journal of Algebraic Geometry; arXiv08092926v2 [mathAG]. * [11] А. Коннес, К. Консани _Схемы над \({\mathbb{F}}_{1}\) и зета-функции_, Compositio Mathematica 146 (6), (2010) 1383–1415; doi:10.1112/S0010437X09004692. * [12] А. Коннес, К. Консани _Характеристика \(1\), энтропия и абсолютная точка_, в Сборнике трудов 21-ой конференции JAMI “Некоммутативная геометрия, арифметика и связанные вопросы”, Балтимор 2009, JHUP (2011); (в печати). arXiv:0911.3537v1 [mathAG]. * [13] А. Коннес, К. Консани _Гиперкольцо классов адель_, Journal iof Number Theory 131 (2011) 159–194. * [14] А. Коннес, К. Консани _От моноидов к гиперструктурам: в поисках абсолютной арифметики_, в Casimir Force, Casimir Operators and the Riemann Hypothesis, de Gruyter (2010), 147–198. * [15] А. Коннес, К. Консани, М. Марколли, _Веселимся с \({\mathbb{F}}_{1}\)_, Journal of Number Theory 129 (2009) 1532–1561. * [16] А. Коннес, М. Марколли, _Некоммутативная геометрия, квантовые поля и мотивы_, Публикации коллоквиума, Том 55, Американское математическое общество, 2008. * [17] К. Консани, М. Марколли, _Квантовая статистическая механика над функциональными полями_. J. Number Theory 123 (2007), no. 2, 487–528. * [18] Б. де Смит, Х. В. Ленстра _Стандартная модель для конечных полей: определение_, http://www.math.leidenuniv.nl/ desmit/papers/standard-models.pdf * [19] Д. Грейсон _Кольца Гротендика и векторы Витта_, Comm. Algebra 6 (1978), no. 3, 249–255. * [20] А. Гротендик _Теория классов Черна_. (Французский) Bull. Soc. Math. France 86 1958 137–154. * [21] Р. Хартшорн _Алгебраическая геометрия_, Градуированные тексты в математике 52, Springer-Verlag, Нью-Йорк Гейдельберг Берлин 1977. * [22] М. Хазевинкель _Векторы Витта. Часть 1_, в: M. Хазевинкель, ред., Справочник по алгебре. Том 6, Elsevier, 2009, 319–472. * [23] М. Хазевинкель _Операции в \(K\)-теории эндоморфизмов_, J. of Algebra 84 (1983), 285–304. * [24] Л. Хессельхольт _Большой де Рам Витт комплекс_, arXiv:1006.3125. * [25] Келли-Спаньер _Характеристики Эйлера_ Тихоокеанский журнал математики 26, 2 (1968). * [26] Х. В. Ленстра, _Поиск изоморфизмов между конечными полями_, Math. Comp. 56 (1991), no. 193, 329–347 * [27] Й. И. Манин, _Лекции о зета-функциях и мотивах (по материалам Денингера и Курокавы)_ Колумбийская Университетская Нумерологическая Школа (1992), Astérisque No. 228 (1995), 4, 121–163. * [28] Д. Мамфорд, _Лекции о кривых на алгебраической поверхности_, Исследования в математической науке, 59, Принстон, Нью-Джерси: Принстонский Университетский Пресс. * [29] Д. Квиллен _О когомол Переведите markdown с английского на русский. Сохраните формулы: